TL;DR
- There are two types of utility functions, ordinal and cardinal.
- Ordinal utility ranks options based on preference level, without indicating the extent of that preference. Example: oranges > bananas > cherries.
- Cardinal utility assigns numerical values to options, indicating preference level and preference intensity. Example: oranges (100) > bananas (50) > cherries (40).
- Utility functions can theoretically be applied to all possible world states, ranking or assigning values to each state based on the satisfaction it would provide to the decision-maker.
- Applying an ordinal utility function to the totality of possible world states would be practically impossible due to the vast complexity of factors influencing each state.
- In everyday circumstances, comparing a small number of world states is usually sufficient. Ordinal utility provides a relational output, indicating preference of one state over another.
- Cardinal utility allows for a single world state to be input and any number to be output, avoiding the need for direct comparison. However, translating a world state into a utility number is disputed.
- The use of world state representations, simplified models of the world, helps to apply utility functions in a manageable way. These representations aggregate components of the world state for easier comparison.
- Proxies, or abstracted positive and negative values, simplify decision-making by serving as representative concepts of our utility functions.
- Some people construct cardinal utility functions from proxies, using an aggregation function to derive a utility value. This is called multi-attribute utility.
- Aggregation is a lossy process, and critics argue that it removes important information from the utility calculation. An alternative is multi-objective optimization, which respects value diversity.
- Proxies play a key role in other ethical theories as well. They act as the foundation for determining moral duties or rules in deontological ethics, and guide decisions towards enhancing moral character in virtue ethics.
Why this article?
When talking about (human) utility functions, I have encountered a lot of confusion and misunderstandings. There are different forms of utility functions that people use interchangeably. Some assume that everybody has a clear-cut ratio-scale utility function that you just need to figure out (e.g., by simple extrapolation). Some of them claim to know exactly the(ir) utility of world state X, Y, and Z. Some others consider the notion of utility functions to be virtually useless or net-negative in utility (figuratively speaking of course). I'd like to provide some clarifications that helped me wrap my head around the notion of utility functions. I won't use any (fancy) math as I don't think, it's necessary to get the message across.
Why Utility Functions?
Understanding human decision-making can often feel like trying to solve an enigma. With a multitude of factors influencing every choice we make, deciphering the underlying logic can seem daunting. That's where the concept of utility functions comes in handy. Utility functions essentially provide a theoretical framework to represent and quantify our preferences. They function as a mathematical shorthand, translating our complex, multi-faceted desires and needs into a form that can be easily analyzed and understood. Whether it's choosing between different flavors of ice cream or making major life decisions like choosing a career path, utility functions allow us to model these choices in a systematic way. Utility functions offer a lens to examine the rationale behind our decisions, thereby enhancing our understanding of human behavior. This makes the study of utility functions not just an intellectual exercise, but a powerful tool in deciphering the complexity of human decision-making.
And of course, EAs and rationalists love dropping the term in every other conversation. Using the term utility function can be immensely helpful when aiming to maximize positive impact or do the most good. The concept of a utility function provides a systematic way to quantify and compare the potential benefits of different actions, thus helping to guide decision-making towards the most effective outcomes. By representing values, goals, or beneficial outcomes numerically, utility functions allow for a structured comparison and prioritization of actions. If, for example, your goal is to alleviate global suffering, you could assign values to different charitable actions based on their estimated impact, thus creating a utility function. This function can then guide you to allocate your resources – like time or money – where they will generate the greatest utility or good.
Ordinal versus Cardinal
As I said, I'm going to skip all the basic mathematical elaborations of the Von Neumann-Morgenstern utility theorem and their axioms and other such mathematical background[1]. I will mostly use plain natural language and supporting images to make my points. Let us consider two types of utility functions: a cardinal utility unction and an ordinal utility function. The concepts of cardinal and ordinal utility functions come into play when trying to measure preferences and satisfaction derived from different choices or outcomes. While both aim to provide insights into preference structures, they do so in distinct ways.
Toy World
The ordinal utility function is the more basic of the two concepts. It is a function that ranks options or outcomes according to the level of satisfaction or preference they offer, without giving any precise numerical measurement of the utility derived. Essentially, it tells us the order of preferences. For example, if you prefer oranges to bananas and bananas to cherries, an ordinal utility function might simply rank these as oranges > bananas > cherries. However, this ranking doesn't tell us by how much you prefer oranges to bananas or bananas to cherries.

The cardinal utility function on the other hand is a function that assigns specific numerical values to different options or outcomes. It not only ranks options according to preference, but also gives an indication of the intensity of those preferences. For example, in the fruit preference scenario, a cardinal utility function might assign a value of 100 to oranges, 50 to bananas, and 40 to cherries. These numerical values indicate not only that you prefer oranges to bananas and cherries, but also that you would take an orange over a banana and over cherries together.

Extension to the Real World
These were very simple examples referring to only one dimension, namely fruits[2]. If we extend the notion of utility functions to the entire world, we would look at something like the following. As input, we take in the set of possible world states and as output, we get the total ordering of all these states. The state of the world here refers to all possible configurations of reality at a given moment, considering every conceivable factor. This includes everything from the macroscopic level – such as the state of global politics, the economy, the environment, social and cultural factors, technological advancement, and more – down to the microscopic level, like individual health status, personal relationships, and even the precise arrangement of atoms in the universe.
To apply an ordinal utility function to this immeasurably large set means assigning a preference ranking or a numerical value to each and every one of these countless world states, based on the satisfaction or benefit they would provide to the decision-maker. This task is, of course, impossible to complete in practical terms due to its sheer enormity and complexity. It would require an impossible level of knowledge and computational ability to even approximate. Nevertheless, it serves as a theoretical ideal, highlighting the ultimate goal of utility theory: to understand and quantify preferences over all possible outcomes. So, when we say we want to "include really anything", we are attempting to grasp the totality of preference structure, considering any and every factor that could affect the decision-maker's satisfaction. This underscores the ambitious scope of utility theory and its goal of providing a comprehensive model of decision-making.
Of course, we could simplify matters. For everyday-purposes, one does not have to create a total-preference-ordering over all possible states. Often, it is sufficient to compare a handful or just two world states. Do you prefer state A over B and C? That is what most people do, most of the time. For example, let's say we have three different world states as shown below. We prefer the left world state over the other two, and the middle one over the right one.
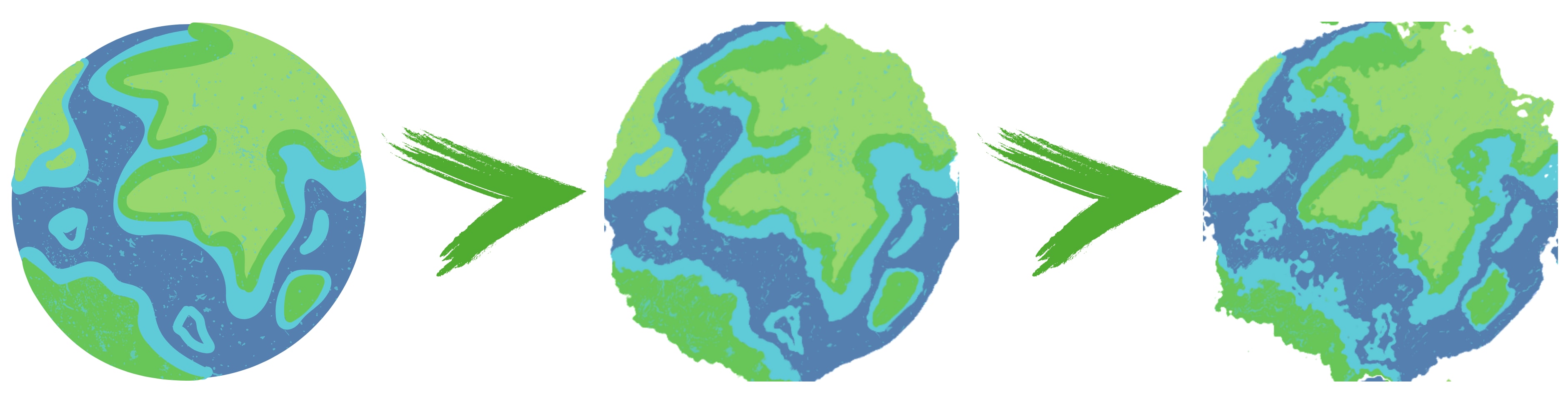
The output of an ordinal utility function is by its nature relational. You can only say that you prefer a state more than another one. But with a cardinal utility function, you can use a single world state as input and output any number. There is no need for direct comparison. The question is though, how do you translate a world state into a utility number? That is, what is highly disputed. Some would claim that this is an arbitrary process, not grounded in explicit functions, but simply opaque intuition.
What is difference here? Aren't both cardinal and ordinal utility functions based on intuition anyway? Well, yes, but ...
If you compare two world states with each other, it is easier to state what you prefer than to assign particular numbers to them. The resolution of your intuition is quite diverging. Comparing two world states with each other has the lowest resolution. A over B? Assigning (float) numbers (e.g., between 0 and 100) to world states which should be comparable in principle and indicate the strength of your preferences seems to be a much bigger ask, implying a way higher resolution. What I'm trying to say here is that maintaining coherency in all your (intuitive) cardinal evaluations is not easy. Analogous to the fruit example, we get a utility value for each world state.

World State Representations
Of course, the planet distortion in the previous images tells you which world state is preferable. This representation is an extremely crude simplification. Things become less obvious if you would choose a slightly different world state representation (WSR). In the figure below, we will go briefly through the transformation steps.
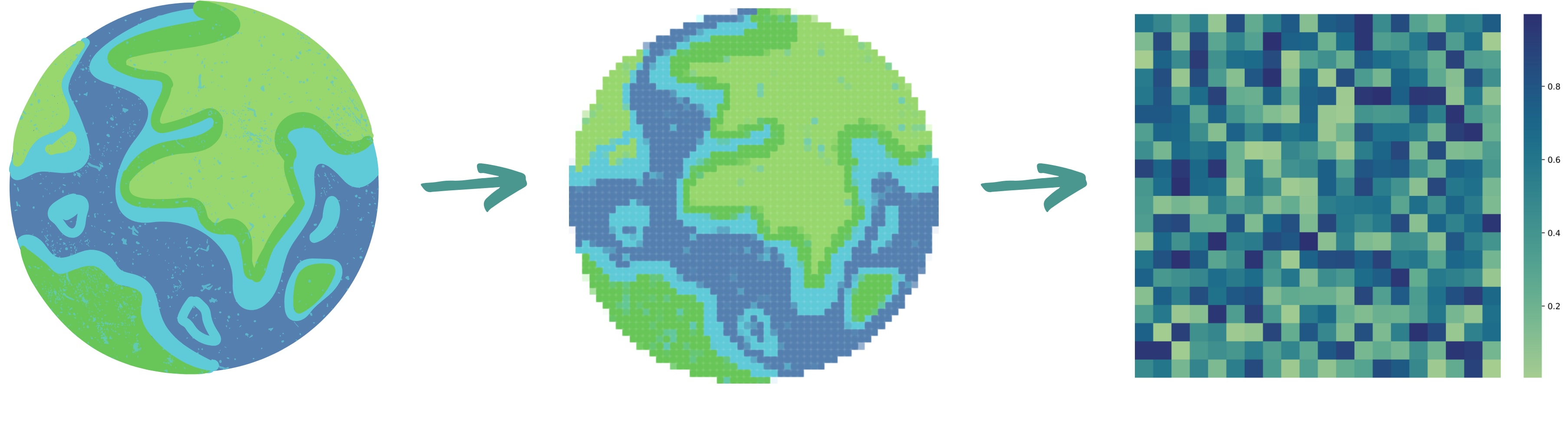
The first WSR is supposed to encompass the entire world with all its details (the impossible kind as discussed above). The second WSR is a pixelated simplification. It shows us that we need to aggregate components of the world state to reduce the dimensions of the first WSR. This aggregation happens on a geographical scale for the pixelated version[3]. The third WSR looks already quite different from the others. The 20x20 grid is not supposed to represent the geography of the world. It's not the geography or physicality in a particular location, that we care about. We usually care about higher aggregates. For this purpose, consider each cell to represent a particular feature of the world that seems reasonable to track. E.g., cell (0,0) represents Gross World Product (GWP). Cell (2,19) represents Total World Population[4][5]. The color represents the degree of a feature's manifestation (which is normalized between 0 and 1). E.g., the higher GWP is, the higher the cell's value and the darker the cell's color. The grid in the third WSR represents a simplified state of the world that is more convenient to work with[6].
Proxies
Let's start with an ordinal utility function applied to this world state representation. Consider three distinct world states and their ranking as shown in the figure below.
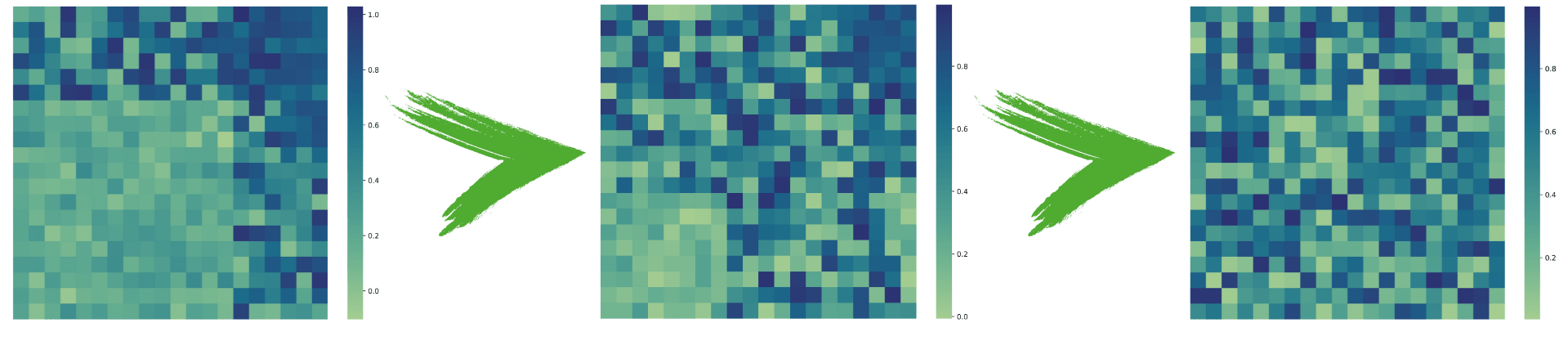
Theoretically, we could rank the set of all possible world states. Given that each cell has a float value between 0 and 1, this would be an impossible task. However, we can easily rank the three given world states. Now, in this example, it is the case, that we are able to hesitantly infer a pattern. It could be the case that we prefer a particular pattern of world states. In this simplified case, we could infer that we might prefer lower values in the lower left corner and higher values in the upper right corner. It seems almost superfluous to say, but humans are intuitive pattern recognizing machines. The real world has too many interacting parts to keep track of entirely. Working with simplifications and finding patterns is what we do well.
Remember that each cell represents a concrete and easily observable feature of reality? What if the pattern is more complex? Maybe it's more than a particular subset of the grid's cells that we care about. Maybe we care about higher abstracted patterns. There might be a pattern within this grid that is not just islands of colors in particular corners. The patterns could be more intricate. You might consider particular valuations of a subset of cells across the grid in very particular combinations to be pleasing. But for simplicity's sake, let us consider the simple island patterns.
How do recognize the patterns usually? After experiencing many world states (e.g. see figure below), we try to extract a pattern that can tell us what we like (good patterns) and what we don't like (bad patterns).
Some of these good patterns, we assign names to such as justice, honesty, kindness, respect, courage, freedom, responsibility, equality, peace, humility, loyalty, tolerance, wisdom, and many more. Bad patterns are sometimes labelled as dishonesty, greed, cruelty, arrogance, apathy, jealousy, prejudice, impatience, manipulation, laziness, hostility, selfishness, pride, vengeance, etc.
Using abstracted (positive and negative) values as proxies for our utility functions makes things easier with respect to decision-making. What's the alternative? Imagine having to rank all 50 world states in the figure above. With each world state having 400 dimensions, this becomes quickly infeasible. And these 400 dimensions are already a crude simplification of the world. In reality, it's almost infinitely higher-dimensional. It's much easier to say: "Hey, I just like bright-lower-left-corner world states and I call them just world states." And even though, these bright-lower-left-corner world states maybe do not encompass fully what you care about and there are some other world state configurations that you would also call just, it's often a good enough approximation to navigate through the world.
From Proxies to Multi-Attribute Utilities
My understanding is that some people don't stop here. Some people try to construct their cardinal utility functions from proxies. Some attempt to use a single proxy (i.e. a single value) as the input to their function. E.g., a high degree of equality is directly translated into a high level of utility. That is of course a very simplified way of looking at proxies and utility. Others go a bit more complex by using a set of proxies of a world state as inputs and return the output as a utility value. For example, take equality, GWP, and freedom in a world state as inputs, use some kind of aggregation function (e.g., addition) and voilà that's the utility of that particular world state. That's what is also called multi-attribute utility. Some use this way of aggregating proxies into a single utility because it's easier to compare single utility values across world states. Especially, if you want to maximize utility, it's just more convenient to have a single value.
However, aggregation is not a lossless process. We actually lose a lot of information. And I think, that's again where a lot of critics jump in, taking cardinal utility functions apart. But multi-attribute utilities are not a route, one has necessarily to take. One could also embrace value diversity and go for multi-objective optimization (if you care about eventual optimization). Pareto-optimality is the right key word here and if you are interested in how that would work, have a look at this section of another forum post.
For now, our journey has followed the depiction of the figure below. We started with a complete description of the world state, transforming the world state into a fewer-dimensional representation (still describing concrete things in the world), inferring proxies (e.g., values), and then using these to potentially arrive at final utility values.
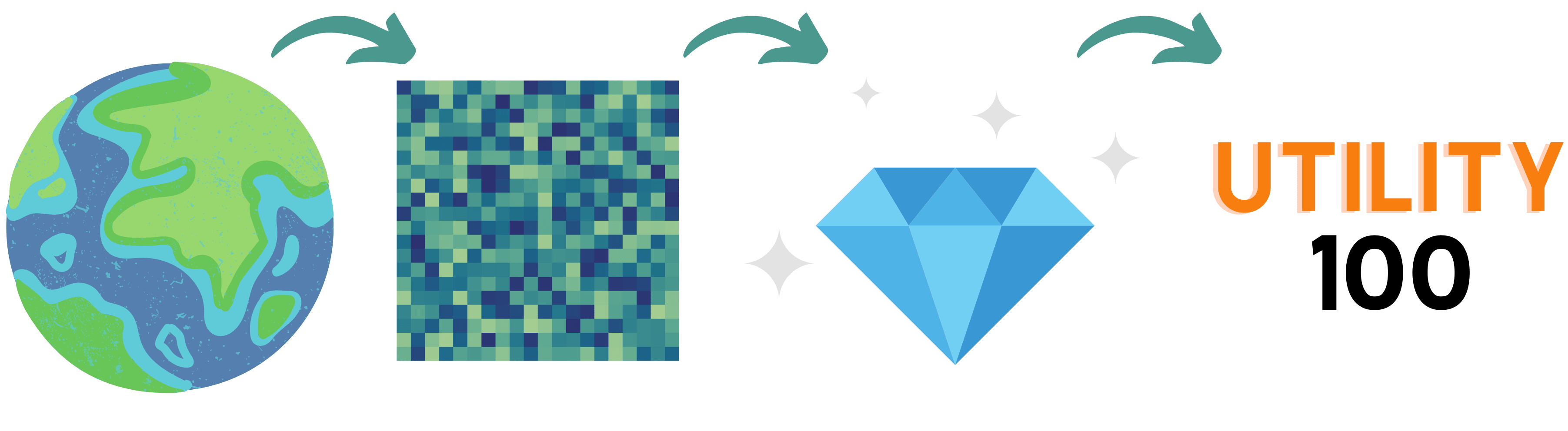
(Multi-attribute) Cardinal utility is the pinnacle of aggregation. We use a combination of ranking and pattern recognition at the grid level representation. We figure out how to crudely describe our internal mechanism for ranking by identifying proxies. And eventually, we can use these proxies to calculate multi-attribute utilities or we stay with the diversity of the proxies (and use Pareto-optimality for optimization).
Proxies in other Ethical Theories
Using an analogy to deep learning, we could say that our intuitive utility function is a black box, mapping world state input to some kind of preference output. Proxies are used to explain what the intuitive utility function might be roughly doing. It can help creating a narrative, finding some kind of patterns in the hyper-dimensional inputs.
Proxies are easier to use than (cardinal or ordinal) utility functions because that's what we do instinctively. This is probably a reason why in sociology, values are considered integral components of the social fabric that shape and direct individual and collective behavior. By studying values, sociologists often like to gain insights into why people behave the way they do, as these values provide a motivational basis for actions and decisions, reflecting societal norms, beliefs, and expectations. I assume this is related to how proxies are used in non-utilitarian ethical theories. Generally, I have the impression that most ethical theories are just different representations of the same thing.
Also in the context of virtue ethics, values can be seen as proxies for utility functions. However, the understanding of "utility" is slightly different here. Instead of the traditional conception of utility as a measure of personal satisfaction or benefit, the "utility" in virtue ethics would align with moral goodness or the development of one's moral character. A decision that aligns with a person's virtues or moral values might not bring immediate personal benefit or satisfaction. Still, it increases their moral goodness, improves their character, or aligns with their understanding of what a morally good life looks like. This enhancement of moral character or alignment with a morally good life could be seen as increasing their "moral utility". So, in the context of virtue ethics, values and virtues serve as proxies for this kind of moral utility function, guiding decisions towards what will enhance moral character or align with a morally good life, even when it might not maximize personal benefit in the traditional sense.
I would argue that proxies also play a crucial role in deontological ethics. They help to establish the moral rules or duties that one should follow. For instance, if truthfulness is a deeply held value, a deontological perspective would dictate a duty to always tell the truth, regardless of the consequences. In this sense, values in deontology serve as the foundation for determining the moral duties or rules to be followed. They may not necessarily be seen as proxies for utility functions (as in consequentialist theories), but they are central to defining what constitutes right and wrong behavior according to the rules or duties that are derived from these values. In a way, deontological rules are the result of observed patterns in various world states.
Conclusion
In conclusion, the concepts of ordinal and cardinal utility functions, while different in their approach, serve as fundamental tools for understanding and quantifying preferences in decision-making. They attempt to map and measure the satisfaction derived from various outcomes.
The world is infinitely complex, and as such, these utility functions often have to work with reduced, simplified representations of it. Proxies, representing higher aggregates of this world, are utilized to make sense of this complexity, with these values providing intuitive patterns and driving preferences. Whether we choose to use cardinal utilities, aggregating these proxies into one quantifiable measurement, or maintain the diversity of proxies for multi-objective optimization, is a choice that depends on our purpose and preference.
Moreover, the use of proxies is not confined to the realm of utility theory. In ethical theories such as virtue ethics and deontological ethics, values and virtues could be seen as proxies that provide guidelines for decision-making, dictate duties and actions, and shape individual and collective behavior. They reflect societal norms, beliefs, and expectations, and help create narratives in hyper-dimensional inputs.
Ultimately, utility functions, ordinal or cardinal, and the use of proxies aim to make the highly complex world navigable, helping us understand preferences and make decisions. However, we must acknowledge the simplification and potential loss of information in this process, and continually refine our models and theories to better represent the intricate, multi-dimensional reality we live in. These kinds of acknowledgements can help us having clearer discussions and a better understanding of human decision-making and behavior.
- ^
If you are really interested in these, I recommend reading the corresponding Lesswrong sequences and posts on that.
- ^
And these fruits are simplified. We could consider other dimensions of them. E.g., brand, ripeness, seasonal conditions, soil quality, transport conditions, etc. But let's keep it simple at this stage.
- ^
This representation is only used to showcase how simplification or aggregation could further look like. We will not further consider this world state representation. The following one is important though.
- ^
E.g., further features could be:
- World GDP
- Total world population
- Average global temperature
- Total global annual precipitation
- Global literacy rate
- Total number of recognized countries
- Number of species on the endangered list
- Total global forest area
- Number of Internet users worldwide
- Global average life expectancy
- Global gender ratio
- Total number of spoken languages
- Global oil production rate
- Total area of the world covered by deserts
- Global CO2 emissions per year
- Total world energy consumption
- Total number of cities with more than a million inhabitants
- Global ocean acidity level
- Total number of patents registered worldwide
- Number of globally recognized natural world heritage sitesThese are random 20 examples. To fill the grid, we would need to identify 380 more features to fill all 400 cells (20x20).
- ^
Keep in mind that most suggested features are comparably concrete and easily observable. We abstained from using extremely abstract features like Freedom, Justice, Love, etc.
- ^
The 2-dimensionality of this representation is randomly chosen. We could also represent the state as simple column vector with 400 (or any number of) entries.
