kaarel
Comments9
I can buy that it is sometimes useful to think about x-risk in terms of a partition of the worlds we could be in, the probability of each part in the partition, and the probability of x-risk in each part. For this to be useful in decision-making, I think we'd want the partition to sort of "carve reality at its joints" in a way that's relevant to the decisions we'd like to make. I'm generally unconvinced that the partition given here achieves this.
My best attempt at trying to grok the partition here is that worlds are grouped according to something like the "intrinsic difficulty" of alignment, with the remaining uncertainty being over our actions to tackle alignment. But I don't see a good reason to think that the calculation methodology used in the post would give us such a partition. Perhaps there is another natural way to interpret the partition given, but I don't see it.
For a more concrete argument against this distribution of probabilities capturing something useful, let's consider the following two respondents. The first respondent is certain about the "intrinsic difficulty" of alignment, thinking we just have a probability of 50% of surviving. Maybe this first respondent is certain that our survival is determined by an actual coinflip happening in 2040, or whatever. The other respondent thinks there is a 50% chance we are in a world in which alignment is super easy, in which we have a 99% chance of survival, and a 50% chance we are in a world in which alignment is super hard, in which we have a 1% chance of survival. Both respondents will answer 50% when we ask them what their p(doom) is, but they clearly have very different views about the probability distribution on the "intrinsic difficulty" of alignment.
Now, insofar as the above makes sense, it's probably accurate to say that most respondents' views on most of the surveyed questions are a lot like respondent 2, with a lot of uncertainty about the "intrinsic difficulty" involved, or whatever the relevant parameter is that the analysis hopes to partition according to. However, the methodology used would give the same results if the people we surveyed were all like respondent 1 and if the people we surveyed were all like respondent 2. (In fact, my vague intuition is that the best attempt to philosophically ground the methodology would assume that everyone is like respondent 1.) This seems strange, because as far as I can intuitively capture what the distribution over probabilities is hoping to achieve, it seems that it should be very different in the two cases. Namely, if everyone is like respondent 1, the distribution should be much more concentrated on certain kinds of worlds than if everyone is like respondent 2.
Note that the question about the usefulness of the partition is distinct from whether one can partition the worlds into groups with the given conditional probabilities of x-risk. If I think a coin lands heads in 50% of the worlds, the math lets me partition all the possible worlds into 50% where the coin has a 0% probability of landing heads, and 50% where the coin has a 100% probability of landing heads. Alternatively, the math also lets me partition all possible worlds into 50% where the coin has 50% probability of landing heads, and 50% where the coin has 50% probability of landing heads. What I'm doubting is that either distribution would be helpful here, and that the distribution given in the post is helpful for understanding x-risk.
Here is another claim along similar lines: in the limit as the number of samples goes to infinity, I think the arithmetic mean of your sampled probabilities (currently reported as 9.65%) should converge (in probability) to the product of the arithmetic means of the probabilities respondents gave for each subquestion. So at least for finding this probability, I think one need not have done any sampling.
If you'd like to test this claim, you could recompute the numbers in the first column below with the arithmetic mean of the probabilities replacing the geometric mean of the odds, and find what the 18.7% product becomes.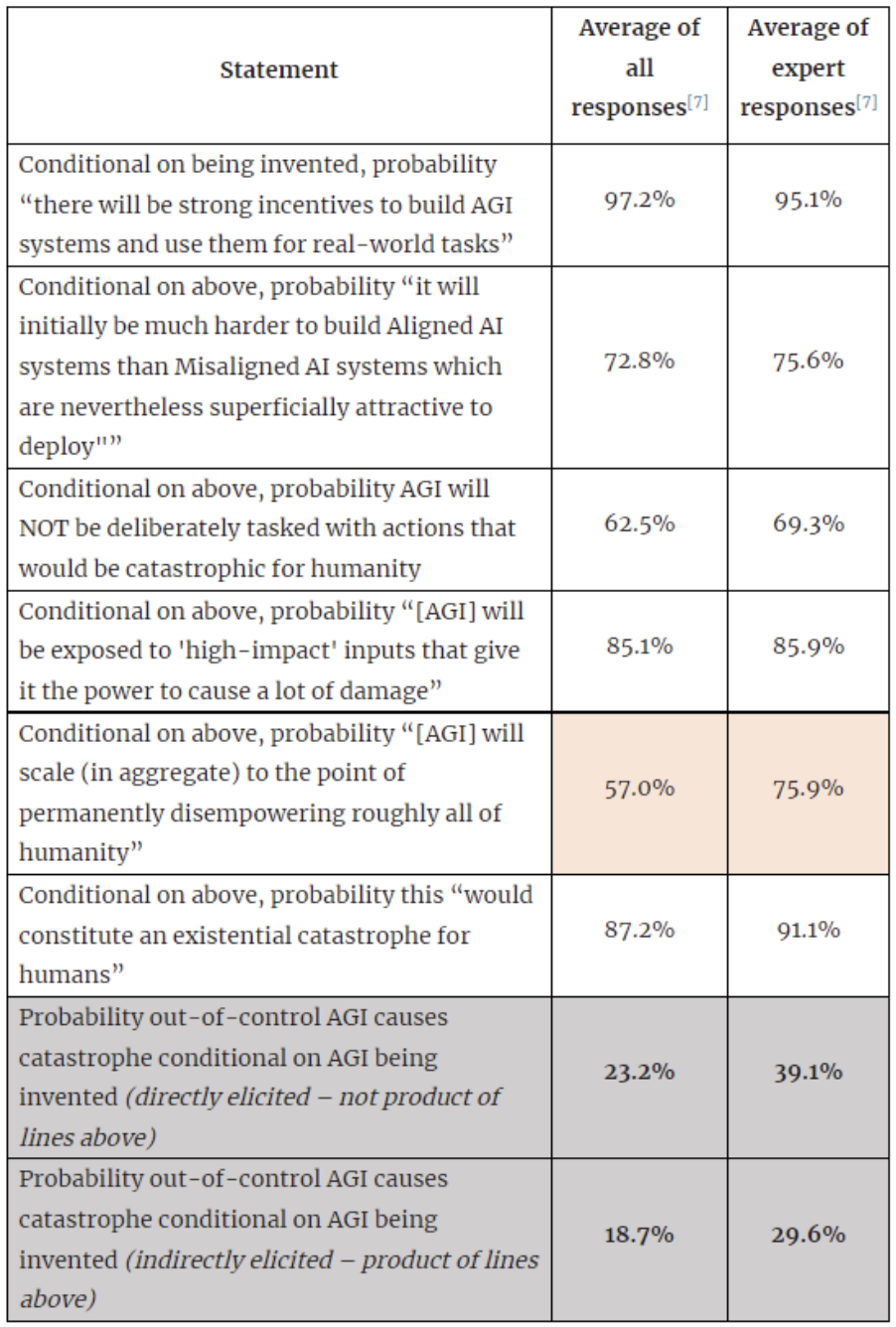
Thanks! That's indeed the quantity I was interested in, modulo me incorrectly thinking that you computed the geometric mean of probabilities and not odds.
Given that you used odds when computing the geometric mean, I retract my earlier claim that there is such a simple closed-form limit as the number of samples goes to infinity. Thanks for the clarification!
[EDIT 1: The following is wrong re the 1.6% number, because that was the geometric mean of odds, not the geometric mean of probabilities as I assumed here.]
By the way, as the number of samples you take goes to infinity, I think the geometric mean of the sampled probabilities converges (in probability) to a limit which has a simple form in terms of the data. (After taking the log, this should just be a consequence of the law of large numbers.) Namely, it converges to the geometric mean of all the products of numbers from individual predictions! So instead of getting 1.6% from the sampling, I think you could have multiplied 42 numbers you calculated to find the number this 1.6% would converge to in the limit as the number of samples goes to infinity. I.e., what I have in mind are the numbers that were averaged to get the 18.7% number below. [EDIT 2: That's not quite true, because the 18.7% was not the average of the products, but instead the product of the averages.]
Could you compute this number? Or feel free to let me know if I'm missing something. I'm also happy to elaborate further on the argument for convergence I have in mind.
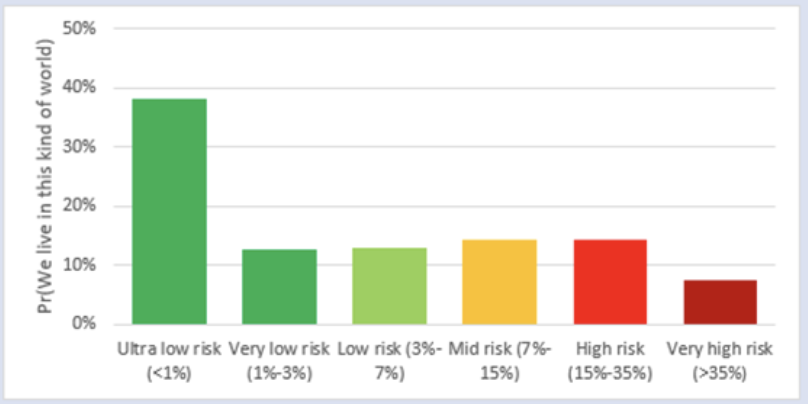
If we actually take these to be the probabilities that we live in various kinds of worlds, then it's just a law of conditional probability that the overall probability is the arithmetic mean of the individual probabilities, not the geometric mean, I believe.
I could imagine ways to philosophically justify taking the geometric mean here anyway, e.g. by arguing that our synthetic samples are drawn from a large community of synthetic experts that is an accurate extrapolation of actual experts, and that it's a good idea to take the geometric mean of forecasts. [EDIT 1: I'm guessing this should be done with odds instead of probabilities though, and that this would bump the answer upward.] [EDIT 2: In fact, it was done with odds already.] But the former seems implausible given that the products of the numbers given by individual experts tend to be larger (in particular, larger mean) than the ones found for the synthetic community – this suggests that experts are giving correlated answers to the different questions. Perhaps we should think that some sort of idealized experts would answer these subquestions independently, but with the same distribution as the empirical one in this sample? It's not clear to me that this is the case. In any case, if there is good reason to take the geometric mean here, I think the analysis could greatly benefit from presenting a clear justification of this, as the answer depends on this up to close to an order of magnitude.
I read your footnote 9 on this question regarding the geometric mean vs the arithmetic mean, and found it confusing. If the picture given in the first paragraph of my comment is indeed what you have in mind, then shouldn't the Brier-score-maximizing prediction still be the arithmetic mean (as that is the all-things-considered probability)? I don't see how the geometric mean would come into play.
(By the way, I'm aware that it doesn't quite canonically make sense to speak of the "tractability" of computing probabilities in a single belief network. But I don't think this meaningfully detracts from what I say above making sense and being true. (+ I guess the translation of the result in this post from math to common language would probably ~equivocate similarly.))
I'm sorry and I might well be missing something, but it seems to me that the main argument in the post is "here is a particular problem with having one's actions guided by models which are so messy as to make calculating probabilities of events impossible". But such models are not used by anyone to make predictions anyway, because they are computationally intractable (a forecaster can't generally use such models to compute probabilities, unless they are secretly in possession of something like something more powerful than a polynomial time SAT-solver)! So since no forecaster is operating with such a model, it seems to me that the post's main argument says nothing about whether what forecasters are actually doing makes sense or not.
The only part of the post that I understand as saying something about [whether [what [people actually assigning probabilities to potential catastrophic events] are doing] makes sense or not] is the response to counterargument 2.
It seems to me that ~all salient belief networks, at least in the sense of belief networks used by people in practice to come up with probabilities in this context, are computationally tractable. (I.e., coming up with probabilities given the model has to be computationally tractable, otherwise people would not be using the model to come up with probabilities.) So it seems to me that the (~only) crucial question here is whether we have reason to think that these particular tractable belief networks would make decent predictions – I understand that this is addressed a little bit in the response to counterargument 2. I don't find that argument convincing at all, but also this is not the main point I'd like to make with this comment. My main point is that it does not look like the main thrust of this post contributes anything to understanding of this ~only crucial question.
So it currently seems to me that the number of paragraphs in this post which address whether longtermist reasoning can be action-guiding is approximately upper-bounded by 2. Again, I feel bad about being harsh here. To say something positive: the stuff about computational complexity is cool on its own! My meta-level guess is that I'm missing something crucial...

Here is one really concrete sense in which deontology is what one gets by Taylor expanding consequentialism up to first order (this is copied from a rambling monograph):