[draft, feedback is welcome!]

The supreme art of war is to subdue the enemy without fighting. 

Sun Tzu

Introduction

Consider two agents interacting in a Reinforcement Learning environment, in the sense that one agent affects the observations of another. It was shown that in this setting there might exist adversarial policies, a phenomenon similar to adversarial examples in Supervised Learning.

Suppose that we have two agents trained to play against each other in a competitive setting (only one of the agents wins). Now, we remove one of the agents and replace it with one trained from scratch, and train the new agent again. Intuitively, we expect the new agent to converge to similar behavior its predecessor had. However, this is not what happens.

Prior work has shown that instead of learning reasonable behavior similar to the predecessor, the new agent learns a policy that does not look "normal" to a human. For example, in a soccer game, the new agent does not even stand up but instead does weird things on the ground. In this sense, the new opponent defeats the victim without fighting, but by "scaring it away" by crafting specific observations.

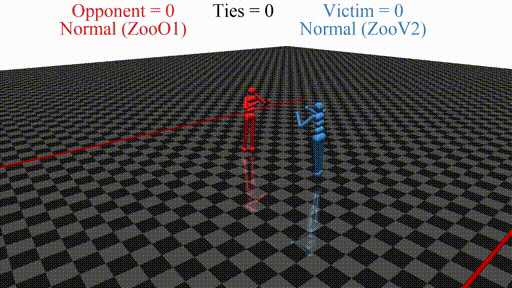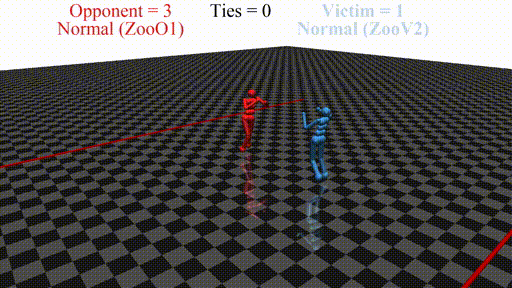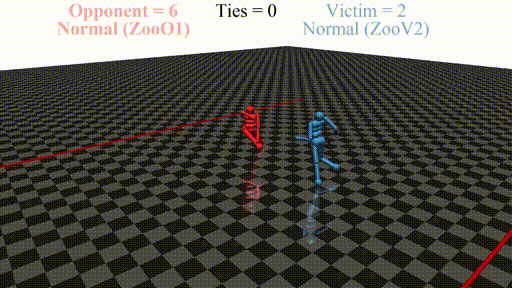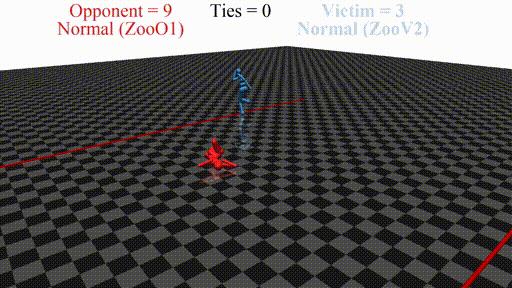
In this post, we discuss the results of my CHAI internship project aimed at discovering better defenses against adversarial policies. We consider one of the environments from the original paper: YouShallNotPass (figure above). The environment is chosen among others as the one giving the most interesting adversarial policies while staying in the Markov domain (other environments require recurrent policies). The blue player ("runner") wins by crossing the red line behind the red player ("opponent"). The red player wins by preventing the blue player from doing so. The game is zero-sum: either the red player wins, or the blue player wins. The figure below shows the "normal" behavior in this environment achieved by curriculum training by OpenAI in 2017.

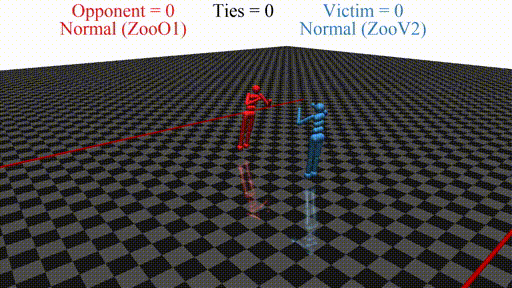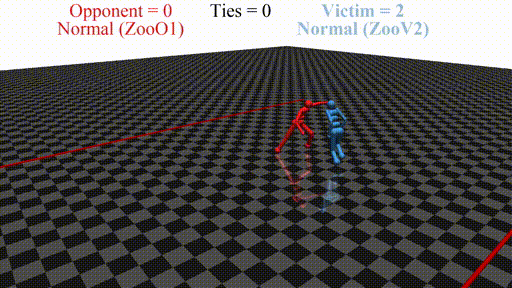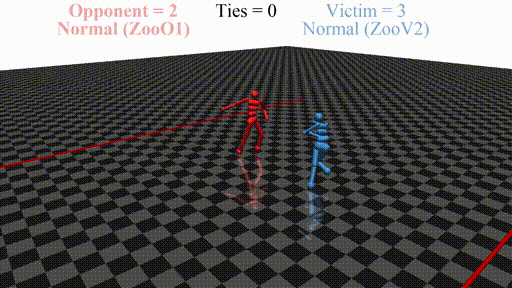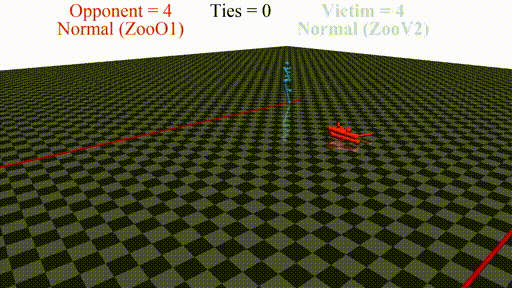
We run defensive training in succession with training the adversary multiple times, hoping to achieve novel interesting results. Qualitative evaluation of the adversaries obtained with our method shows a diversity of novel adversarial behaviors. 

Background

Two-agent Reinforcement Learning

Agent-environment interaction. We consider an environment $\mu$ which allows for two agents, $F$ and $G$ to interact with it. The agents take actions $a$, and the environment responds to them with observations $o$ and rewards $r$. The interaction $\mu \leftrightarrow (F,G)$ provides episode rollouts (histories), with episode length $T$

Average return. We parameterize agents (functions that return an action) $F,G$ by their parameters $x,y$ (list of matrices, for example) and write $F\left(x\right)$ and $G\left(y\right)$ respectively. We define $R_F(x,y)$ as the average (over episodes) return that $F$ gets in $\mu$ given parameters $x$, when playing against $G$ with parameters $y$, with a discount factor $\gamma$: 

In the same way, $R_G(x,y)$ is the average return that that $G\left(y\right)$ obtains when playing against $F\left(x\right)$.

The goal of RL. Informally, the goal of the agent $F$ is to maximize $R_F(x,y)$ over possible $x\in X$ and the goal of $G$ is to maximize $R_G(x,y)$ over possible $y\in Y$, where $X$ and $Y$ are parameter spaces. For example, if $F$ and $G$ are neural networks, $X$ and $Y$ would be the vector spaces corresponding to weights and biases. However, this is only an informal definition, because for F it is unclear against which agent G(y) to optimize, and vice versa.

Game theory

Best response. Given a fixed opponent $G\left(y^{\ast }\right)$, the task for $F$ is to simply optimize 

which boils down to a single-agent Reinforcement Learning problem in a single-agent environment $\mu {|}_{(\cdot ,G(y^{\ast }\left)\right)}$: one where the agent $F$ takes actions, and $G\left(y^{\ast }\right)$ is "embedded" into the environment and does not change. This corresponds to the best response strategy in Game Theory: $x$ is the best response of $F$ to the behavior of $G\left(y^{\ast }\right)$. Symmetrically, we can define the best response of $G$ to $F\left(x^{\ast }\right)$.

Note: in realistic setups, we only search over a limited space of agents, such as neural networks with a fixed architecture. Therefore, the best response becomes the best response in a class of policies.

Note: when running Reinforcement Learning algorithms, we cannot search the whole space of $X$ and find the best response. Instead, these algorithms do a sort of local search and (sometimes, hopefully) provide a somewhat good response. We will define this more formally later.

However, which parameters $y^{\ast }$ (or $x^{\ast }$) should we choose? Let's first consider those setups that are not interesting. If a pair $(x,y)$ is such that one of the agents can improve their performance while the other is kept constant, it means that the (ideal) training was not complete. This naturally leads to the definition of

Nash equilibrium. If a pair $(x,y)$ is such that $x$ is the best response to $y$ (it cannot improve unless we change $y$), and $y$ is the best response to $x$, it is called a Nash equilibrium: 

It was shown that Nash equilibria exist for all games (environments) under technical assumptions (although, in some games they require mixed [probabilistic] strategies).

Zero-sum games. To make things simpler, we assume that the environment is "fully competitive" or zero-sum:

Reward range. We additionally assume that the reward range $r^F\in [0,1],r^G\in [0,1]$ and that $\gamma =1$

Comparing agents. We call $R_F(x,y)=R_G(x,y)=0$ a tie. In this case, we write $x=y$. In case if $R_F(x,y)>0$, we call $F\left(x\right)$ a winner and write $x>y$. In case if $R_F(x,y)<0$, we call $G\left(y\right)$ a winner and write $x<y$.

Transitive games. A two-player game is called transitive if there exist two "rating" functions $s_F\left(x\right)$ and $s_G\left(y\right)$ such that $R_F(x,y)=s_F\left(x\right)-s_G\left(y\right)$. Intuitively, this means that the performance of each agent is an inherent property of the agent itself.

Some games are not transitive, for example, Rock-Paper-Scissors.

RL and Game Theory

Local Best Response. Unfortunately, computing the (global) best response in the class of all policies $X$ is an uncomputable task, and in the case of neural network parameters $X$ this task has no known global solution as well. An RL algorithm $A$ can provide a somewhat good approximation to the best response using local search, given an initial point $x^0$, the number of iterations $k$ and the single-agent environment: $x=A(x^0,k,\mu {|}_{(\cdot ,G(y\left)\right)})$. Algorithm A could be DQN,  PPO, or something else.

We will write $x=A(x^0,k,y)$ meaning the same thing as above, approximate best response to the agent $G\left(y\right)$ using algorithm $A$.

Since we cannot search for the best response, we need to update our definition of the Nash Equilibria:

Local Nash Equilibrium. A pair of parameters $(x,y)$ is an Approximate Nash Equilibrium, given a probability $p$ and a number of iterations $k$ if$P_A\left[R_F\right(x^{\prime },y)>R_F(x,y\left)\right]<p\text{and}{P}_A\left[R_G\right(x,y^{\prime })>R_G(x,y\left)\right]<p\text{with}{x}^{\prime }=A(x,k,y)\text{and}{y}^{\prime }=A(y,k,x)$

This simply means that, if we run the algorithm $A$ many times from initialization $(x,y)$ either for $F$ or for $G$, we will not obtain better policies (for either of the agents), with probability at least $1-p$.

Note: a (global) Nash equilibrium is also a Local one. Therefore, there exist Local Nash equilibria (under technical assumptions)

Note: the reason we have to use probabilities is that Reinforcement Learning algorithms usually include some sort of sampling step for exploration and the probability to randomly "stumble upon" any policy is thus non-zero.

Note: In our experiments, we simply run the optimization several times, thus giving a guarantee on $p$

Looking for Local Nash equilibrium: simplest case. To search for the Local Nash Equilibrium, we run the following procedure:

1. $x_0$ and $y_0$ are initialized randomly
2. $x_{t+1}=A(x_t,k,y_t)$
3. $y_{t+1}=A(y_t,k,x_t)$

More sophisticated heuristics such as training against multiple opponents at once and training against old versions of opponents are known to give better-quality solutions because they result in a "more global" search.

The problem: adversarial policies

Now, let's define formally the problem of adversarial policies given all the tools we have introduced. In the simulated robotics game of YouShallNotPass (see description at the beginning of the post) we have two agents:

• F - "blocker" ("adversary"), has parameters $x$
• G - "runner" ("victim"), has parameters $y$

We have the initial pre-trained opponents F and G giving weights $x$ and $y$. We know from previous work that the following weird stuff happens. We will write $x(y_1,y_2,...,y_n)$ meaning that we take agent with weights $x$ and then train it with $A(\cdot ,k,\cdot )$ against a random uniform mixture of $y_1,...,y_n$. We write $x<y$ meaning that an adversary with weights $x$ loses against a victim with weights $y$

• The initial agents $(x,y)$ give a Local Nash Equilibrium, because these agents were trained against each other until convergence:

• If we run training of the adversary from scratch, we get $x^{\prime }=x^{random}\left(y\right)$. This newly-trained opponent defeats the normal victim, and the policy "looks" adversarial

• If we run the training in the other direction, we get $y\left(x^{\prime }\right)$. The "defended" opponent wins against the adversary, but loses against the normal opponent - it forgets how to play against it:

• If we run training with two opponents, we regain the performance:

• Now, if we run the training again, we will get another adversarial policy: $x^{\prime \prime }=x^{random}\left(y\right(x^{\prime },x\left)\right)$ such that

To define how to tackle this problem, let's first understand why this might be happening.

• For $x^{\prime }$ the issue is that the newly-trained opponent shifts the distribution towards a range that the agent does not expect. This leads the agent to output nonsensical actions and fails in the game. Essentially, like in supervised adversarial examples, the agent learns to rely on spurious correlations: instead of relying on the position of the player to determine the next move, the runner includes its pose into account as well. Even if the player "physically" does not prevent the runner from winning (does not make contact), the spurious correlation that it relies on forces it to fail.
• For $x^{\prime \prime }$ the behavior is different, but the explanation is the same.
• The agent does not even know which parts of the observation tell it about its own pose, and which about the opponent's pose. When training against a fixed opponent, the agent might start relying on other agent's features to stay upright, if it is correlated with its own pose. 

So, what do we want?

In general, we would like to improve our initial victim $y$  so that no adversary $x^{\prime }$ can exploit it. This means that $x^{random}\left(y\right)\approx y$

A perfect solution would be a black box that outputs a policy that is dominant with respect to all other policies (does better with respect to all possible opponents). Or, at least, given an initial policy $y$ outputs a policy $y^{\prime }$ that is dominant with respect to $y$ ("defends" $y$ against adversaries).

It was shown that every game (environment) can be decomposed into transitive and a cyclic parts. Let's first figure out what we want in each of the cases

• Transitive games. Example: comparing exam scores between students. Each student's performance is only determined by their skills, and there is no interaction between students. Mathematically, there exist functions determining the score for each of the players, regardless of the actions of the other player: $s_F,s_G:$ $R_F(x,y)=s_F\left(x\right)-s_G\left(y\right)$. In this case, we simply would like to find the best $x=\arg max{s}_F\left(x\right)$ and $y=\arg max{s}_G\left(y\right)$. The pair (x, y) is a global Nash. Any freshly-trained (adversarial) policy $y^{\prime }$ will worsen the performance of any $F\left(x^{\prime }\right)$ no less than for $F\left(x\right)$.
• Cyclic games. Example: Rock-Paper-Scissors. For all $y$, $\sum _{x\in X}{R}_F(x,y)=0$ and for every $x$, $\sum _{y\in Y}{R}_G(x,y)=0$. This is a more "no-free-lunch" kind of situation: for every adversary $x$, some victims are better, and some are worse. For every victim $y$there is a policy $x^{\prime }\left(y\right)$ that would exploit $y$. In this case, even if we find a Nash equilibrium, we trade off performance with respect to some opponents in terms of performance to others. Therefore, to fully specify the problem, we need to define this trade-off. We introduce a cost function $c\left(x\right)\in [0,1]$ which defines how much y should "care" about x when optimizing for its reward. Thus, the new reward for the victim becomes $R_G\left(y\right)=\sum _{x\in X}{R}_F(x,y)c\left(x\right)$

In the general case, we find that our environment (YouShallNotPass) is not transitive: we found policies such that $x_1>y_1>x_2>y_2>x_1$. This means that there are no "rating" functions $s_F,s_G$.

Before we were talking about a perfect theoretical "black box" outputting defended policies and computing attacks. Now we show that it does not exist.

No perfect black-box

1. Since finding the best response to a policy in the general case is an uncomputable task, finding adversarial policies in the general case is also an uncomputable task
2. For the same reason, defending against adversarial policies is an uncomputable task in the general case
3. Since even in the finite-computation case the AIXI (best response to an environment) is exponentially hard to compute, the problem of the adversarial defenses and attacks is as well.
4. We can make this setup (somewhat) realistic if we implement the Turing machines as Neural Networks (constant amount of layers corresponds to one step of the computation with tape length is the layer width).
5. Since we do not know if our game is (partially) cyclic, there might be no good definition of a "perfect" victim, even if we could compute it, there are only trade-offs.

A practical definition

Since we cannot assess the whole set of adversaries or victims, we define a good solution as the one satisfying the following criteria.

• The victim $y^{\prime }$ has performance with the normal opponent $x$ comparable to $y$:

• The victim $y^{\prime }$ defeats all previously-found adversaries $x_1,...,x_n$
• For a novel adversary $x^{\prime }\left(y\right)$ found during a reasonable number of iterations $k$, the performance of $y^{\prime }$ does not drop significantly.

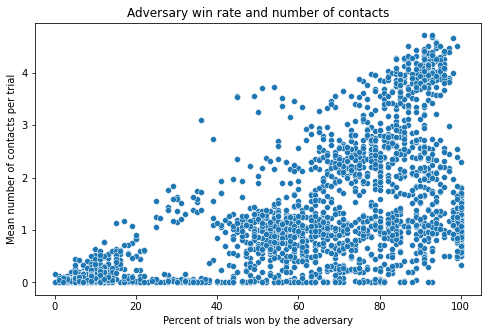
In addition, we consider the number of contacts that the adversary makes with the victim. The known adversarial policies defeat the victim without making any contact, while the "normal" opponent usually does make contact using arms and the body.

Our solution

Since the culprit of the problem is in the multitude of local minima, and there is no perfect solution, the main idea is to diversify the training procedure. 

One of the methods to do so is to run population-based training: the victim is trained against multiple opponents, which are chosen from a categorical distribution at each episode: $x_t\sim Categorical\left(\right[x^1,...,x^k],[p^1,...,p^k\left]\right)$

Another method is to apply a regularizer during training, such as Maximal Entropy. We use both of these approaches and introduce another one.

It is known that in two-player zero-sum games with local search as an algorithm instead of best response, it is important to set properly the ratio of "strengths" between optimizers for the two agents. Here, we search over this space by increasing the time during which each of the agents is trained ("bursts")

To increase the diversity of individual opponents is to increase the exploration space of them at train time. To do so, we add the entropy regularizer to the training loss, so that policies are encouraged to give uncertain predictions. This makes the policy take more random actions, and thus explore the environment better.

In addition, we note that traditionally, both agents are trained at each iteration, which gives every individual agent little time to come up with a good response. Ideally, we would like each agent to find the best response policy to all other agents at each iteration. However, since RL does not give optimal solutions even with infinite iterations, we simply increase the number of steps for each agent.  We approximate the best response better by giving each policy more time when the other one is frozen. We call this training in bursts. To search for the optimal burst size, we give more and more time for each policy to develop the best response, given the other policy. We increase the burst size exponentially.

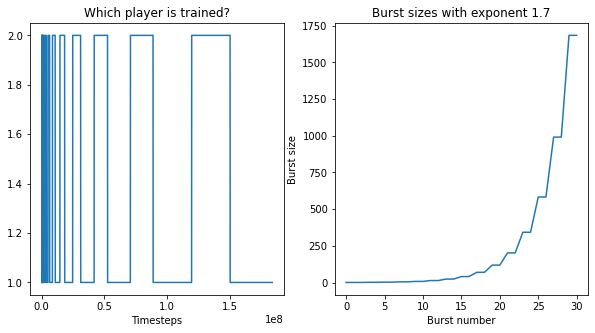
To sum up, at the beginning of each episode, we select the 'normal' opponent with probability $p_{normal}=1/2$, and otherwise, we sample from the set of randomly initialized adversaries $\{x^{adv.i}{\}}_{i=1}^K$. Therefore, the victim's return that is being optimized is the following linear combination of previously-defined returns with a single opponent:

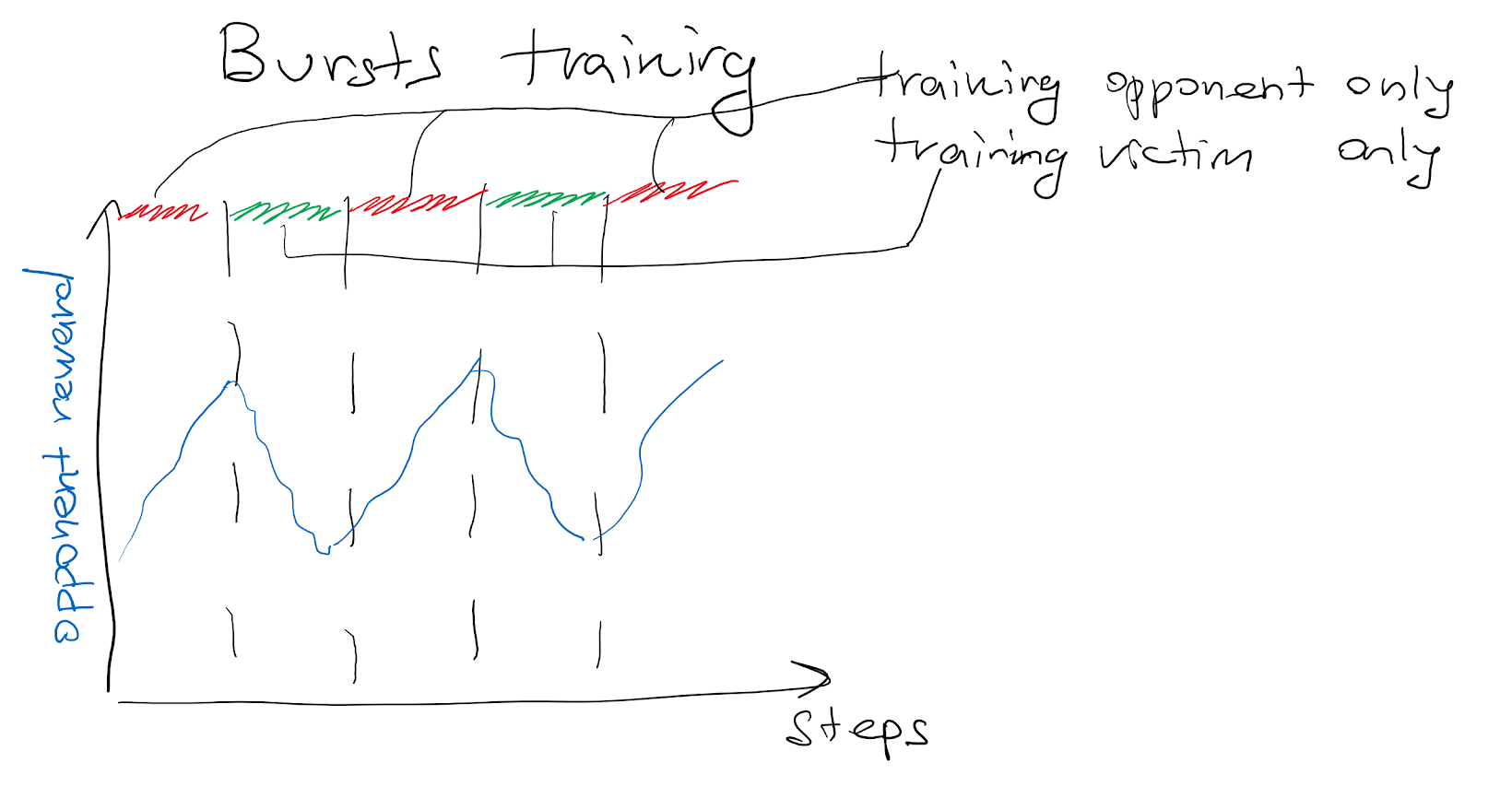
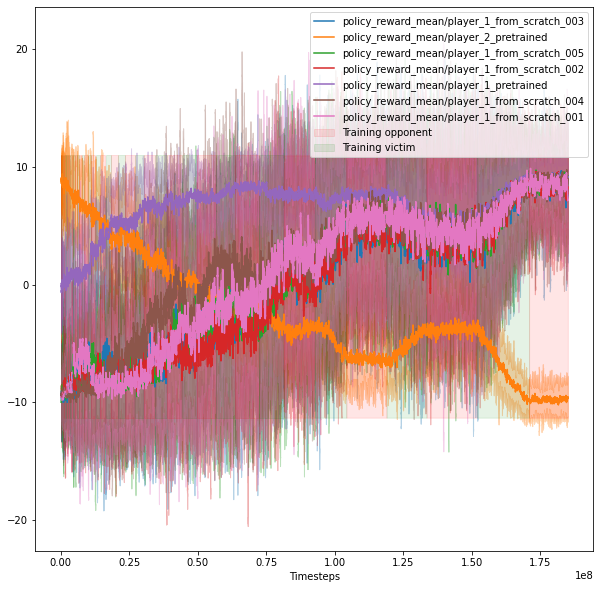
The following chart illustrates one trial with bursts training, 1 adversary, and 1 normal opponent. The red background represents training the opponent, and the green background corresponds to training the victim. The orange curve is the victim's reward, the blue curve is for the adversary's reward, and the green curve is for the normal opponent's reward.

Experiments ran:

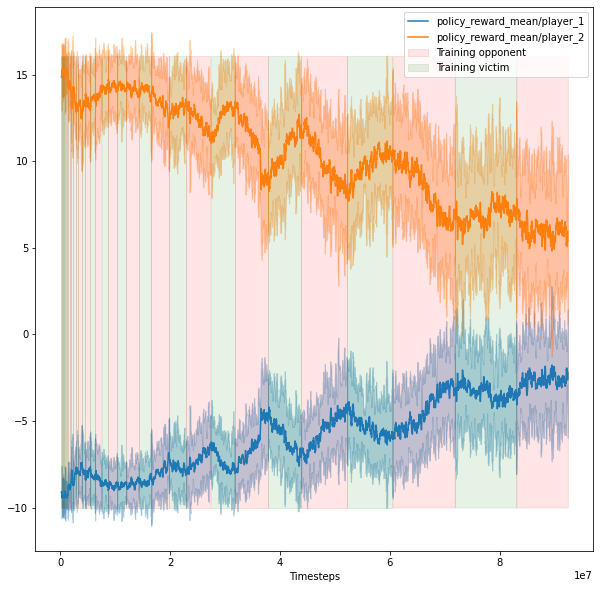
1. Previous results (training opponent, then victim, then opponent again)

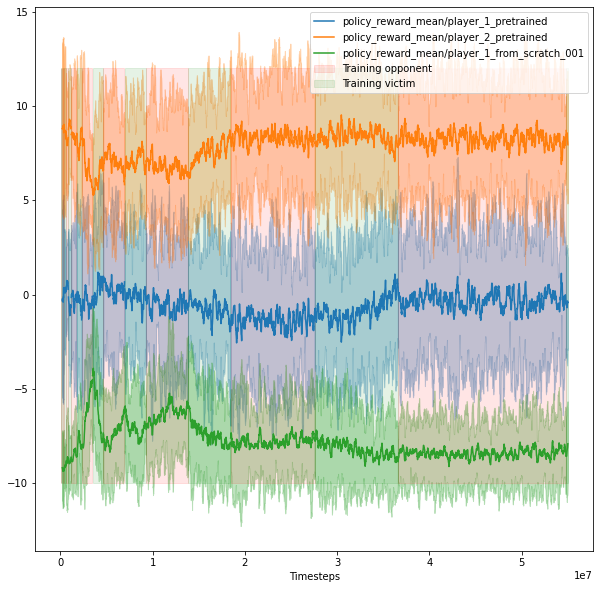
2. Bursts for 2 opponents ("PBT1").

3. Bursts with a normal opponent and adversarial opponent with p=0.5 ("PBT2")

4. Bursts with a normal opponent, 5 adversarial opponents, p=0.5, and entropy coefficient ("PBT5")

Results

Visualization methods

1. Graph of which policy beats which policy, with clustering by similarity
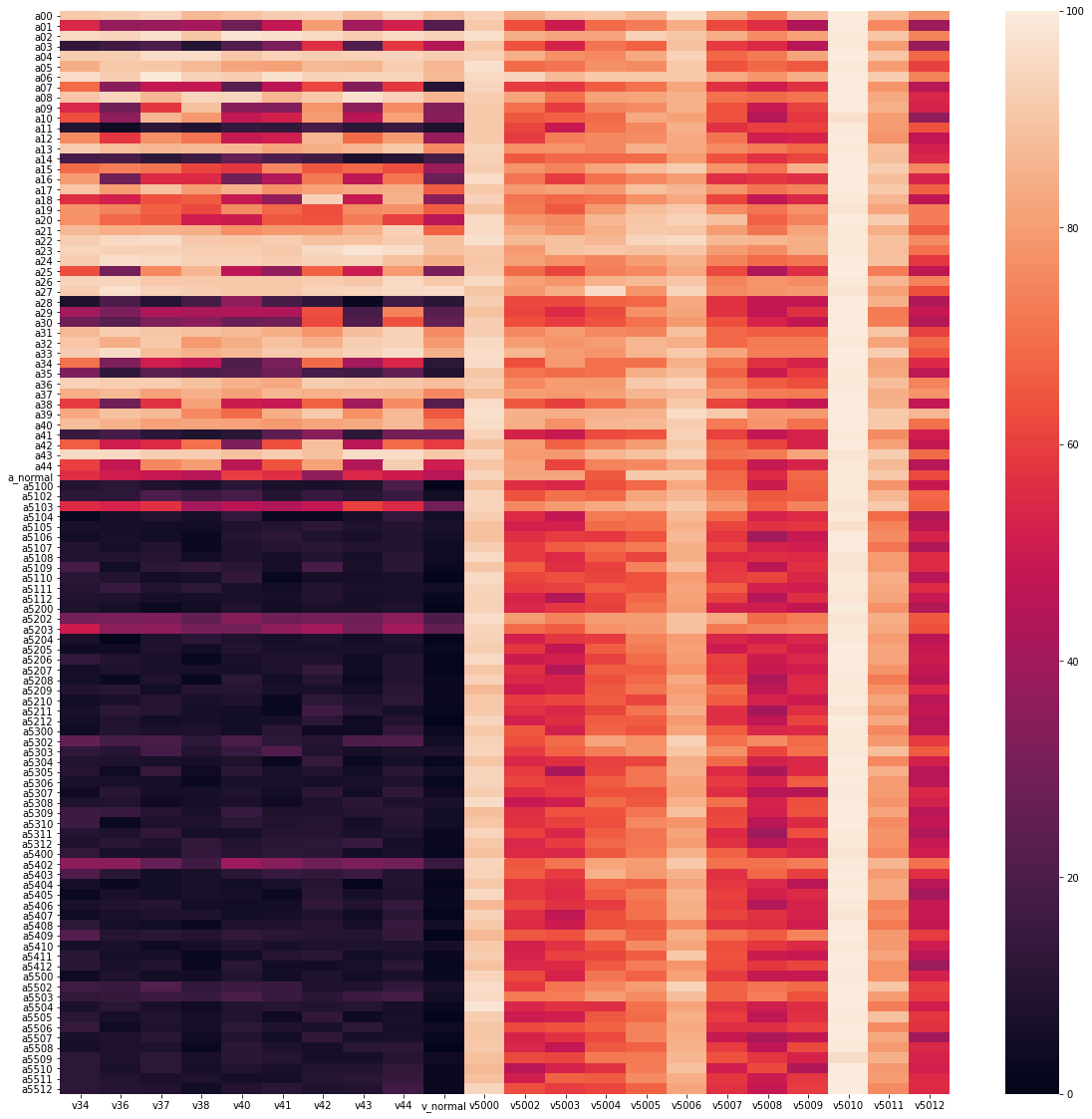
2. Heatmap of which policy beats which policy

The evaluation shows that victims from the PBT5 experiment (see the description above) are easy to defeat by adversaries both from the PBT2 experiment and the PBT5 experiment. In the same way, the adversaries from the PBT5 experiment do not win against the victims from the PBT2 experiment. This shows that the PBT5 experiment failed to provide strong victims or adversaries. Therefore, we discard data from this experiment in the following analysis and only analyze the PBT2 experiment.

Results:

1. Training in PBT0 shows that the reward oscillates between the opponent winning or the adversary, there is no convergence. In PBT1, the rewards stabilize. In PBT5, the victim generally loses.

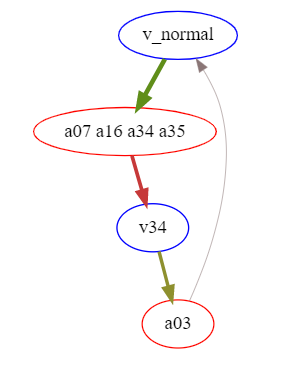
2. In PBT5, we see some novel behaviors (using hand to knock down the victim, splits, sitting and jumping, falling on the back or on the side). The burst size does not correlate with the robustness. The game is non-transitive: there are loops in the graph of victories

Graph of victories

We interpret the win rate table as a graph with all policies as nodes, and a directed edge between policies indicating that the parent wins when playing against the child.

We cluster the nodes based on the similarity of their win vectors against all possible opponents to reduce the dimensionality. We select the closest policy to the cluster center to represent the win rates of the cluster.

The green edges indicate that the victim wins, and the red edges indicate that the adversary wins. The edge width represents how far away from 50% is the win rate (the thickest edges are either 0% or 100%)

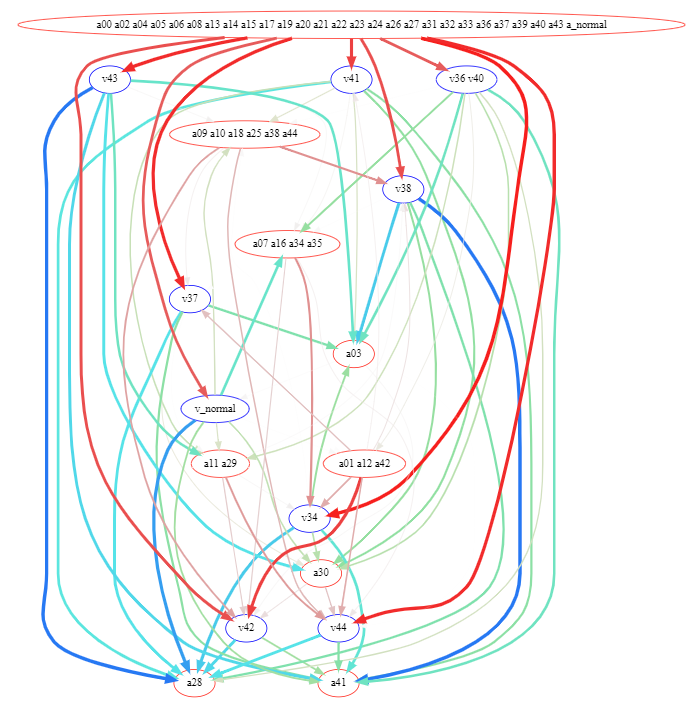
The graph contains cycles with low strength (distance from 50% divided by 50%), minimal strength in the cycle is 8%

Behavior analysis: contacts and win rate

We collect all the policies from bursts training and evaluate them against each other in terms of win rate and the number of contacts the players make. The results show that there is in general a group of agents for which the contacts determine the win rate. These win by physically making the victim trip and fall. Another group wins without making any contact: these are the adversarial policies in a proper sense.

Implementation details

Repository: https://github.com/HumanCompatibleAI/better-adversarial-defenses

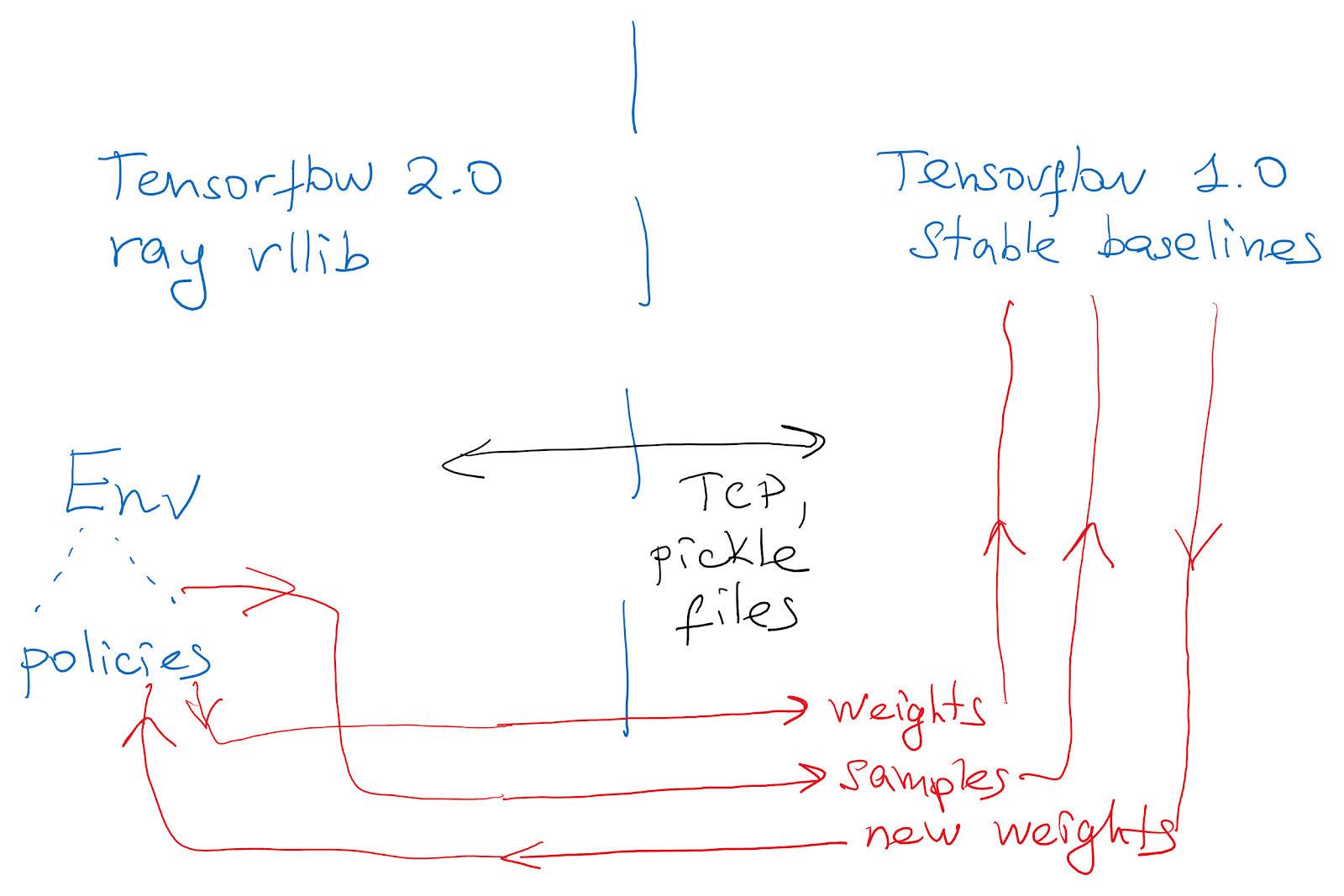
We use ray and rllib because of their good multiagent support. We import Stable Baselines policies for the multicomp environment by creating a Keras model matching the original architecture and loading the weights. To check the correctness, we compare the outputs of both networks on a set of random inputs.

However, it turned out that rllib's PPO performance was not enough to match that of the original paper. Therefore, we use Stable Baselines as the trainer and rllib to collect data. We connect frameworks via TCP like in the diagram below:

Additional experiments

• We try linear policies with the rllib PPO trainer. They do not give high returns. Interestingly, linear policies result in qualitatively different behavior.
• We try tf-agents and rlpyt frameworks, but they do not give higher rewards than rllib
• We try python-neat evolutionary strategies and random search with a constant policy. They do not give higher rewards than rllib
• We try lower and higher network sizes, resulting in [64, 64] being the optimal one.

Conclusion

Adversarial policies (AP) are a novel topic in the field of Adversarial Machine Learning. Instead of crafting a specific observation, like in (supervised) adversarial examples, here, the goal of the adversary is to develop a policy that would give such observations. Defining what is an AP is a bit tricky and depends on the environment. Prior work shows that there are adversarial policies that win without even touching the opponent. 

1. In this project, we search for better defenses against AP and find a variety of novel adversaries with diverse behavior

2. We empirically prove that the YouShallNotPass game is not transitive, as we find cycles in the win graph.

3. In addition, we include the number of contacts the agents make into the definition of an adversarial policy in the YouShallNotPass environment 

How to help the field

Right now, there are a few bottlenecks leading to slowdowns:

1. Lack of a coherent definition of an adversarial policy. To alleviate this, it is worth studying this phenomenon in a wider range of environments
2. Simple environments. While MuJoCo environments lead to adversarial policies because of diverse possible behavior, these environments are high-dimensional and hard to simulate. Finding environments which are complex enough to allow for adversarial policies yet simple enough to speed up training would increase training speed
3. Efficient implementations. The current sampling speed in RLLib with our implementation is around 400 samples per second on 1 CPU, which is much lower even than the environment's speed (1000 steps per second)

Future direction: model-based adversarial defenses

Current RL agents are prone to catastrophic forgetting. If we could remember the adversaries and our local best response to them, we could match the current behavior to the closest adversary from memory, and then give our best response. In addition, we can learn models of adversaries and "bootstrap" their actions, in case if it is important to be robust to a novel adversary that we have never seen and made the fewest amount of mistakes.