Charlie_Guthmann
Bio
pre-doc at Data Innovation & AI Lab
previously worked in options HFT and tried building a social media startup
founder of Northwestern EA club
Posts 10
Comments268
Thanks for the post — There is definitely a certain fuzziness at times about value claims in the movement and I have been critical at times of similar things. Also chatgpt edited this but (nearly) all thoughts are my own hope that's ok!
I see a few threads here that are easy to blur:
1) Metaethics (realism vs anti-realism) is mostly orthogonal to Ideal Reflection.
You can be a realist or anti-realist and still endorse (or reject) a norm like “defer to what an idealized version of you would believe, holding evidence fixed.” Ideal Reflection doesn’t have to claim there’s a stance-independent EV “out there”; it can be a procedural claim about which internal standpoint is authoritative (idealized deliberation vs current snap judgment), and about how to talk when you’re trying to approximate that standpoint. I'm not saying you claimed the opposite exactly but language was a bit confusing to me at times.
2) Ideal Reflection is a metanormative framework; EA is basically a practical operationalization of it.
Ideal Reflection by itself is extremely broad. But on its own it doesn’t tell you what you value, and it doesn’t even guarantee that you can map possible world-histories to an ordinal ranking. It might seem less hand-wavy but its lack of assumptions makes it hard to see what non trivial claims can follow. Once you add enough axioms/structure to make action-guiding comparisons possible (some consequentialist-ish evaluative ranking, plus willingness to act under uncertainty), then you can start building “upward” from reflection to action.
It also seems to me (and is part of what makes EA distinctive) that EA ecosystem was built by unusually self-reflective people — sometimes to a fault — who tried hard to notice when they were rationalizing, to systematize their uncertainty, and to actually let arguments change their minds.
On that picture, EA is a specifc operationalization/instance of Ideal Reflection for agents who (a) accept some ranking over world-states/world-histories, and (b) want scalable, uncertainty-aware guidance about what to do next.
3) But this mainly helps with the “upward” direction; it doesn’t make the “downward” direction easier.
I think of philosophy as stacked layers: at the bottom are the rules of the game; at the top is “what should I do next.” EA (and the surrounding thought infrastructure) clarifies many paths upward once you’ve committed to enough structure to compare outcomes. But it’s not obvious why building effective machinery for action gives us privileged access to bedrock foundations. People have been trying to “go down” for a long time. So in practice a lot of EAs seem to do something like: “axiomatize enough to move, then keep climbing,” with occasional hops between layers when the cracks become salient.
4) At the community level, there’s a coordination story that explains the quasi-objective EV rhetoric and the sensitivity to hidden axioms.
Even among “utilitarians,” the shape of the value function can differ a lot — and the best next action can be extremely sensitive to those details (population ethics, welfare weights across species, s-risk vs x-risk prioritization, etc.). Full transparency about deep disagreements can threaten cohesion, so the community ends up facilitating a kind of moral trade: we coordinate around shared methods and mid-level abstractions, and we get the benefits of specialization and shared infrastructure, even without deep convergence.
It's true - Institutionally, founder effects + decentralization + concentrated resources (in a world with billionaires) create path dependence: once people find a lane and drive — building an org, a research agenda, a funding pipeline — they implicitly assume a set of rules and commit resources accordingly. As the work becomes more specific, certain foundational assumptions become increasingly salient, and it’s easy for implicit axioms to harden and complexify over time. To some extent you can say that is what happened, although on the object level it feels like we have picked pretty good stuff to work on in my view. And charitably, when 80k writes fuzzy definitions of the good, it isn't necessarily that the employees and org don't have more specific values, it's that they think its better to leave it at the level of abstraction to build the best coalition right now. And also that they are trying to help you build up from what you have to making a decision.
I don't see this strain of argument as particularly action relevant. I feel like you are getting way to caught up in the abstractions of what "agi" is and such. This is obviously a big deal, this is obviously going to happen "soon" and/or already "happening", it's obviously time to take this very serious and act like responsible adults.
Ok so you think "AGI" is likely 5+ years away. Are you not worried about anthropic having a fiduciary responsibility to it's shareholders to maximize profits? I guess reading between the lines you see very little value in slowing down or regulating AI? While leaving room for the chance that our whole disagreement does revolve around our object level timeline differences, I think you probably are missing the forrest from the trees here in your quest to prove the incorrectness of people with shorter timelines.
I am not a doom maximilist in the sense that I think this technology is already profoundly world-bending and scary today. I am worried about my cousin becoming a short form addicted goonbot with an AI best friend right now - whether or not robot bees are about to gorge my eyes out.
I think there are a reasonably long list of sensible regulations around this stuff (both x-risk related and more minor stuff) that would probably result in a large drawdown in these companies valuations and really the stock market at large. For example but not limited to - AI companionship, romance, porn should probably be on a pause right now while the government performs large scale AB testing, the same thing we should have done with social media and cellphone use especially in children that our government horribly failed to do because of its inability to utilitize RCTs and the absolute horrifying average age of our president and both houses of congress.
it's quite easy, I actually already did it with printful + shopify. I stalled out because (1) I realized it's much more confusing to deal with all the copyright stuff and stepping on toes (I don't want to be competing with ea itself or ea orgs and didn't feel like coordinating with a bunch of people. (2) you kind of get raked using a easy fully automated stack. Not a big deal but with shipping hoodies end up being like 35-40 and t shirts almost 20. I felt like given the size of EA we should probably just buy a heat press or embroidery machine since we probably want to produce 100s+.
Anyway feel free to reach out and we can chat!
here is the example site I spun up, again not actually trying to sell those products was just testing if I could do it https://tp403r-fy.myshopify.com/
Thank you for writing this. To be honest, I'm pretty shocked that the main discussions around the anthropic IPO have been about "patient philanthropy" concerns and not the massive, earth shattering conflicts of interest (both for us as non-anthropic members of the EA community and for anthropic itself which will now have a "fiduciary responsibility"). I think this shortform does a pretty good job summarizing my concern. The missing mood is big. I also just have a sense that way too many of us are living in group houses and attending the same parties together, and that AI employees are included in this + I think if you actually hear those conversations at parties they are less like "man I am so scared" and more like "holy shit that new proto-memory paper is sick". Conflicts of interest, nepotism, etc. are not taken seriously enough by the community and this just isn't a new problem or something I have confidence in us fixing.
Without trying to heavily engage in a timelines debate, I'll just say it's pretty obvious we are in go time. I don't think anyone should be able to confidently say that we are more than a single 10x or breakthrough away from machines being smarter than us. I'm not personally huge in beating the horn for pause AI, I think there are probably better ways to regulate than that. That being said, I genuinely think it might be time for people to start disclosing their investments. I'm paranoid about everyone's motives (including my own).
You are talking about the movement scale issues, with the awareness that crashing anthropic stock could crash ea wealth. That's charitable but let's be less charitable - way too many people here have yolo'd significant parts of their networth on ai stocks, low delta snp/ai calls, etc. and are still holding the bag. Assuming many of you are anything like me, you feel in your brain that you want the world to go well, but I personally feel happier when my brokerage account goes up 3% than when I hear news that AI timelines are way longer than we thought because xyz.
Again kind of just repeating you here but I think it's important and under discussed.
Tangential to the main post but I just read your shortform comment on less wrong and really agree. From a variety of different anecdotal experiences, I'm getting increasingly paranoid about trusting anyone here regarding ai opinions. How can I trust someone if 50% of their money is in Nvidia and snp 5 delta calls? if we pause AI they stand to lose so much. I don't think this is a small amount of the community either.
( I have most of my money in snp stock and ~15% specifically in tech stocks so I'm still quite exposed to AI progress but significantly less than a lot of people here and I still find myself rooting for ai bull market sometimes because i'm selfish).
benchmarking model behavior seems increasingly hard to keep track off.
I think there are a bunch of separate layers that are being analyzed, and it's increasingly complicated the degree to which they are separate.
e.g.
level 1 -> pre-trained only
level 2 -> post-trained
level 3 -> with ____ amount of inference (pro, high, low, thinking, etc.)
level 4 -> with agentic scaffolding (Claude code, swe agent, codex)
level 5 -> context engineering setups inside of your agentic repo (ACE, GEPA, ai scientists)
level 6 -> The built digital environment (arguably could be included partially in level 4, stuff like api's being crafted to be better for llms, workflows being re written to accomplish the same goal in a more verifiable way, ui's that are more readable by llms).
In some sense you can boil all of this down to cost per run, like ARC, but you will miss important differences in model behavior on a fixed frontier.
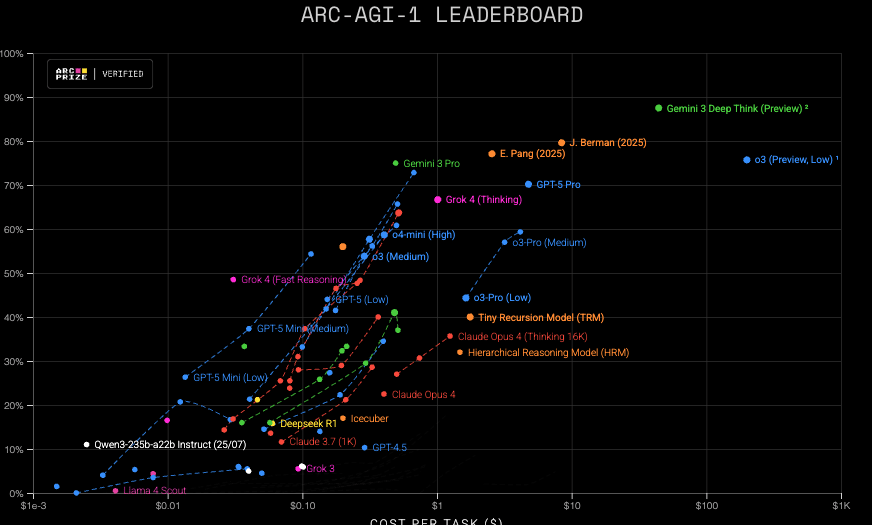
https://jeremyberman.substack.com/p/how-i-got-the-highest-score-on-arc-agi-again
if you read J. Berman substack, you will see he uses existing llms to get his scores with an evolutionary scaffolding (hard to place this as being level 4/5). While I'm decently bitter lesson pilled, It seems plausible we will see proto-agis popping up that are heavily scaffolded before raw models reach that level (though also plausibly we might just see the really useful, generalizable scaffolds get consumed by the model soon thereafter). The behavior of j bermans system is going to be different than the first raw model to hit that score with no scaffolding and pose different threats at the same level of intelligence.
How politicized will AI get in the next (1,2,5) and what will those trends look like?
I think we are investing as a community more in policy/advocacy/research but the value of these things might be heavily a function of the politicization/toxicity of AI. Not a strong prior but I'd assume that like OMB/Think tanks get to write a really large % of the policy for boring non electorally dominant issues but have much less hard power when the issue at hand is like (healthcare, crime, immigration).

Just finding about about this & crux website. So cool. Would love to see something like this for charity ranking (if it isn't already somewhere on the site).
Don't you need a philosophy axioms layer between outputs and outcomes? Existential catastrophe definitions seems to be assuming a lot of things.
Would also need to think harder about why/in what context i'm using this but "governance" being a subcomponent when it's arguably more important/ can control literally everything else at the top level seems wrong.