Summary
This post overviews a cost-effectiveness estimation method that uses program, funding, and institutional counterfactual impact data. The objective is to offer a framework for impact cost-effectiveness calculation that is simple, comprehensive, and broadly applicable, including to longtermist projects. This has not yet been publicly formalized and can be valuable to impact-related decisionmaking. Using this framework in lieu of only counterfactual program impact data can help prevent harvesting prima facie low-hanging fruit and target actually low-hanging fruit, which considers also funding and institutional counterfactuals.
I thank Saulius Simcikas for asking valuable clarification questions about an earlier draft of this post.
Program impact
Program impact is the change of the outcome metric over the course of the program compared to a counterfactual. It is measured by statistical methods, such as randomized controlled trials (RCTs).
[Program impact is the difference between the change of the outcome metric value for beneficiaries (A) and comparable non-beneficiaries (B) over the course of the program. Image: Randomized Controlled Trials)]
For example, if beneficiaries use nets in 75% of cases and if these are not provided for free, only 10% of beneficiaries purchase them; a net covers 2 people, prevents 1 case of malaria per month, lasts for 2.5 years, and cost with distribution $5; and malaria is lethal for 1 in 30,000 patients, then a net directly provides 2*12*2.5*0.75/30,000=0.0015 lives ($1 provides 0.0015/5=0.0003 lives or 1 directly saved life is for $3,333 in this example). Considering that counterfactually, 10% of beneficiaries purchase nets, then the cost of saving a life is about 10% higher (1-0.1)*0.0015/5 = 0.00027 lives/$, or $3,704/life. This number would have been different with a different counterfactual (e. g. 90% of beneficiaries purchasing a net), thus, program impact counterfactual should be considered in cost-effectiveness calculations.
Funding impact
Funding impact is the sum of impact gains due to funders’ decisions. This includes direct, forgone, leveraged, enabled, and influenced investments.
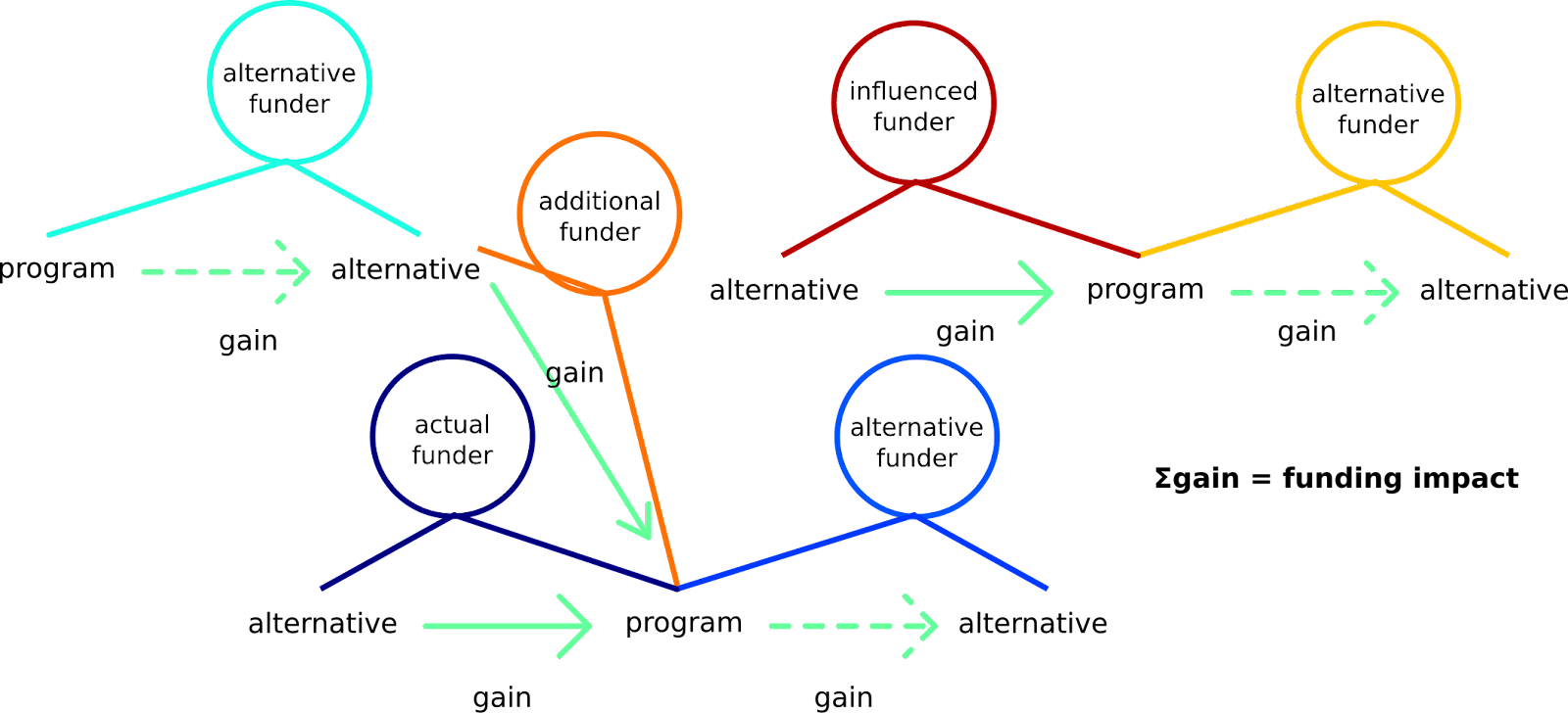
For example, consider that actual funder A invests $1,000 into bednets, while forgoing investing into a painting. She enables an alternative funder B to divest from the bednets to improve a road and motivates an additional funder C, who would have otherwise invested $2,500 into deworming, to invest the $2,500 into bednets. Alternative funder D realizes that deworming tablets are needed, so they forgo their $2,500 project on researching the relative importance of deworming and malaria prevention, from the perspective of the beneficiaries, and invest the $2,500 into deworming that C divested from. An influenced funder E hears that people are divesting from the research on malaria vs. deworming and seem to invest more into bednets, so they divest from baldness research and fund malaria chemoprevention research, since the disease seems to be popular. They are unaware that an alternative funder F would have actually invested into malaria chemoprevention research if they did not fund it, but since this is funded, F spends on researching mosquito welfare, since they think that if they find something important, it can have a significant impact. In reality, the funding landscape is much more complex than this. However, it stays that the sum of impacts of all investments and divestments is the funding impact.
In this simplified case, the funding impact is:
($1,000 + $2,500) on buying bednets (approximately 1 life saved) - painting wellbeing impact + improved road - $2,500 worth of deworming drugs + $2,500 worth of deworming drugs - research on malaria vs. deworming - baldness research + malaria chemoprevention research + mosquito welfare research. This simplifies as:
1 life saved - painting wellbeing impact + improved road - research on malaria vs. deworming - baldness research + malaria chemoprevention research + mosquito welfare research.
Institutional impact
Institutional impact is the change of total impact made across the future. It can be visualized as the sum of changes in the areas under the curves on the (marginal) impact per (marginal) investment vs. cumulative investment graphs across all impact areas.
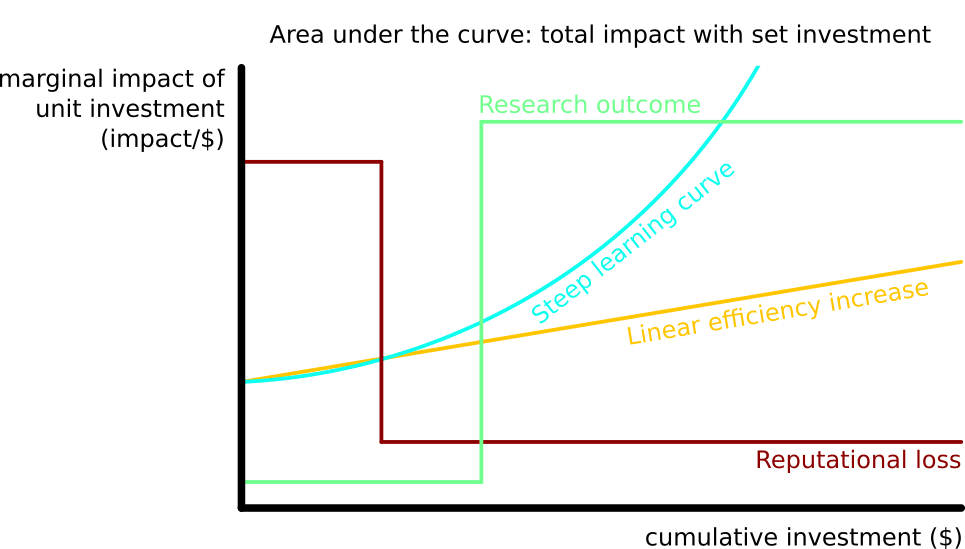
For example, assume that the efficiency of saving lives by providing bednets is constant with increased funding up to the value of $2m, $3,500 per life saved. In addition, it costs $1m to develop a vaccine for malaria. With the vaccine, a life is saved for $500. A funder with $2m can either invest into benets or research and vaccination. In the former case, they save 2m/3.5k=571 lives; in the latter case they save 1m*0+1m/500=2000 lives. If institutional impact is not considered, investors may miss the low-hanging fruit of researching vaccines due to its low marginal cost-effectiveness and opt for a prima facie low-hanging fruit of purchasing bednets. Thus, the development of cost-effectiveness with increasing funding should be estimated and the impact of total funding, when invested optimally, should be considered rather than momentary marginal cost-effectiveness. This is a simplified case: in reality, any additional step changes the projected cost-effectiveness of a large number of interventions, so a complex continuously updated model should be used.
Conclusion
In conclusion, impact cost-effectiveness can be estimated by gathering program, funding, and institutional counterfactual impact information.