Summary

A great deal of EA focuses on saving lives as cheaply as possible. However, due to population pressures, the very premise that saving lives is good may be ill-founded. If saving a life results in more suffering than it alleviates, presumably we shouldn't do it. This post explains why, even if the life saved is net-positive, the intervention can still have a net-negative effect.

The Malthusian Gradient

I first came across the malthusian trap in the June newsletter. In summary, it's the idea that a population will keep growing, up until resource constraints prevent it from further expansion, resulting in a majority of people on the edge of starvation. Advances in agricultural methods may provide a boost to wellbeing, but unless economic growth is maintained, the population will sooner or later expand to sap up the surplus created by the advances. That's the basic idea - read the link in the newsletter for a more thorough explanation.

While it's clear that the malthusian trap is undesirable, what's less clear is how it impacts the effectiveness of charity intervention. Should we save a life in a malthusian-trapped country? What about countries which aren't in a malthusian trap, but are close (i.e., population pressures are the primary cause of extreme poverty in that country, but there's room for some more people)?

The answers depends on your population ethics; but to what extent?

For the following analysis, I'll assume some form of utilitarianism: that the best outcome is the one with the greatest utility; that each additional life has some associated value which adds to the utility; and that the utility of a life is lower if that life suffers more.

Consider how we might plot a graph of utility against population, whereby a utility of 1 is defined as a standard, happy life (think of it as a measure of quality-adjusted lives):

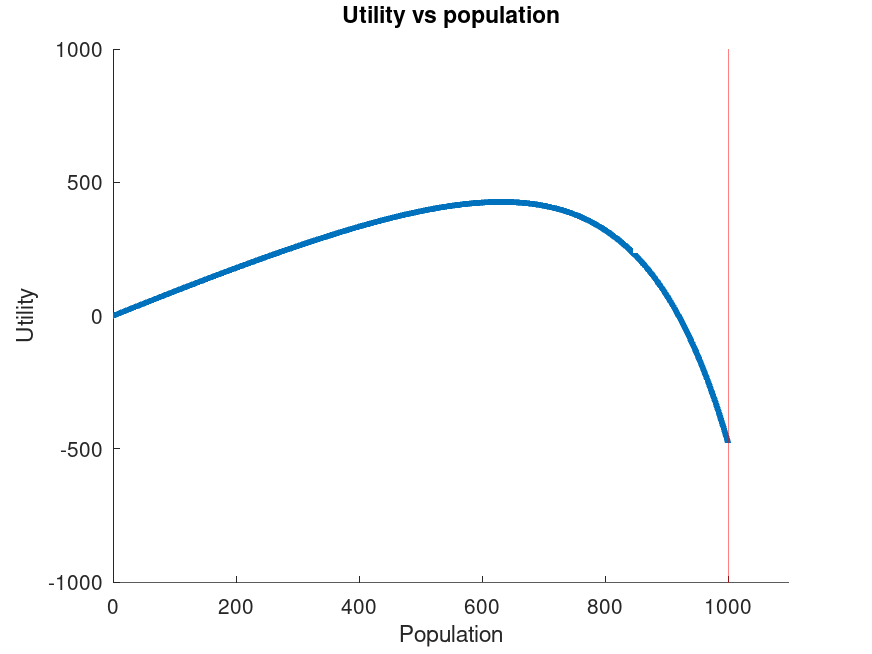
It starts at zero, and grows linearly with a gradient of 1 to begin with: everyone is happy, and the addition of a new person has no detrimental impact on the wellbeing of the rest of the population. 

At the other extreme, when the population is in a malthusian trap (the red line at a population of 1000), the total utility is likely negative - it's hard to imagine suffering more extreme than a life on the edge of starvation!

Filling in the gap, at some point the utility must reach a turning point, beyond which it starts going down. In this case, that's a population of a bit above 600.

Let's define the "malthusian gradient" as the slope of the population-utility curve. For each additional life, the number of quality-adjusted lives changes by the malthusian gradient.

Impact on Effectiveness

Returning to charity intervention, we can now use the malthusian gradient as a multiplier in determining impact.

If an intervention saves 100 lives, and the malthusian gradient is 0.5, then the actual impact in terms of quality-adjusted lives is 50. More worryingly, if the gradient is -0.5, then the impact is a negative 50: we've made the situation worse!

What's actually happened is we've saved someone's life, but that means there's a little less for everyone else, whose combined increased suffering outweighs the benefit of the additional life.

Different Population Ethics

Some people will disagree with my statement that lives in a malthusian-trapped country have negative utility. But even if we change that, it's still likely that there's a region of negative slope:

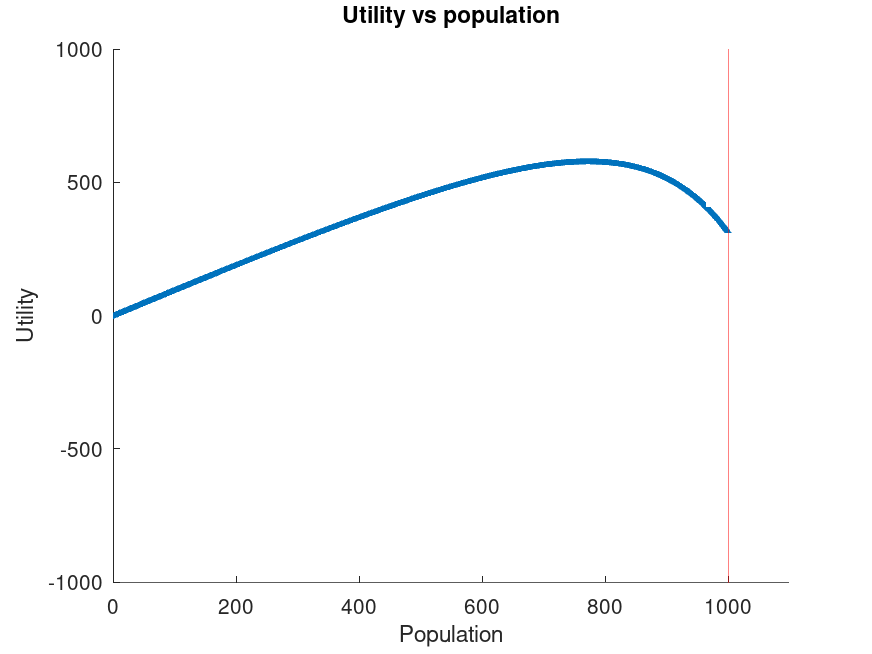
Here the utility at the malthusian limit is positive, and yet a population above 800 yields a negative gradient.

The key point here is that, even if the life saved is net-positive, it can have a net-negative impact on the number of quality-adjusted lives.

The Malthusian Trap in the Real World

How close are real third-world countries to the malthusian trap? This study suggests that parts of East Africa are already there. It also seems plausible that population pressures in many other countries yield a negative malthusian gradient, or at least a gradient significantly less than one.

Impact on Donations

How should this change what causes we fund?

• It makes interventions focused on saving lives in the poorest countries relatively less attractive
• It makes interventions targeting sustained economic growth relatively more attractive

Limitations

This model makes some big assumptions, meaning you should take it with a pinch of salt:

• It makes assumptions about population ethics (I would be interested to see the model extended to other ethical viewpoints)
• Related to that, assigning a utility to a life is a thorny ethical decision that's highly subjective. The graphs in this post are completely arbitrary mathematical functions that are about the right shapes
• The model assumes a uniform utility across the population, which is obviously complete nonsense. How much this affects the conclusions, I don't know
• I've ignored the temporal aspects of population change. The malthusian trap predicts what happens in the long run, so it's not immediately obvious what impact an additional life has in the short term
• A population that's currently experiencing population pressures may be doing much better in 15 years time, meaning lives saved today wouldn't have the negative impact predicted
• I haven't presented much data on this, so it's hard to evaluate where the model is applicable and to what extent

Thoughts are much appreciated.