Why Cost-Effectiveness ≠ Effectiveness/Cost

Disclaimer

Although I do have a lot of experience in math, this article has not yet been thoroughly peer-reviewed. Check with someone with expertise on the topic before using this formula.

(So far, it has been peer-reviewed by a math teacher with wide-ranging mathematical expertise.)

Notes

For this article, I will be using "Expected value" and "impact" interchangeably. 

TL;DR

It's actually the average increase in effectiveness per increase in cost, divided by cost, and it seems that the two calculations just so happen to be different.

But why?

To show why this is, we'll use the help of our friend, pigeon, and statistician in training, Todd.

Todd wants to estimate the expected happiness per rock (the currency the pigeons use) of donating to Jeremy's Flavored Crumb Stand. Todd decides to calculate the expected impact of one extra rock donated with the following formula.

Here's the data.

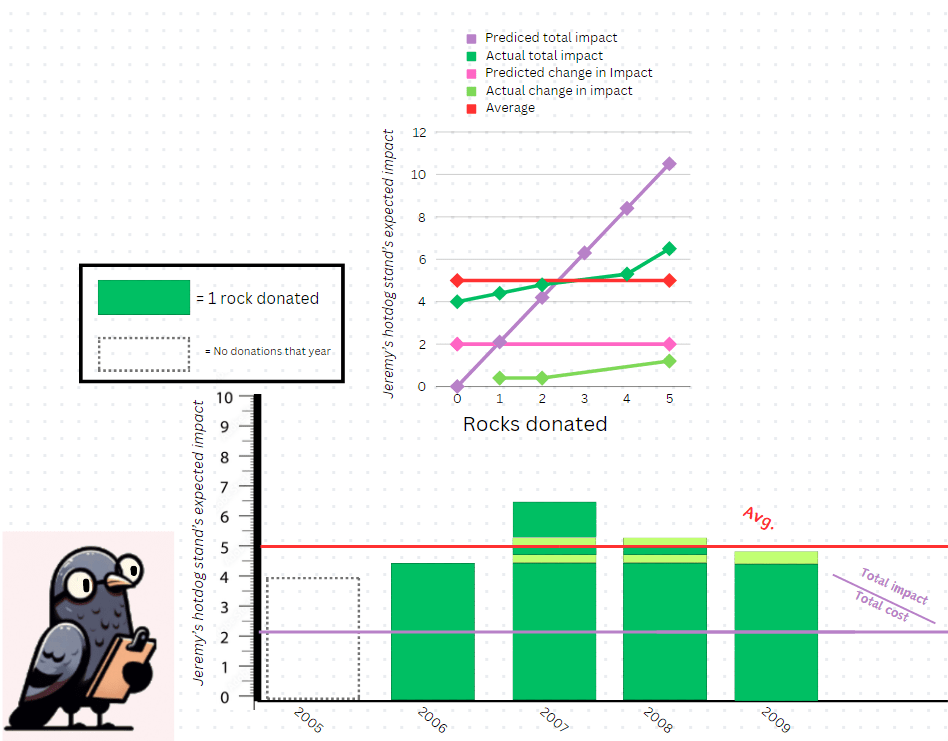
^[1] This doesn't seem very sensible. This estimate is way too high! The projected change in impact (What we're interested in) is much higher than all of the actual changes in impact!

Todd explains his problem to his statistics professor, Taylor. Taylor explains to Todd, "Since we're trying to find $E\left(V_h\right(N+1)-(V_h\left(N\right))$ ^[2], and $E\left[X\right]={\sum }_{x}x\cdot P_X\left(x\right)$ ^[3][4], the cost-effectiveness of donating rocks to Jeremy's Flavored Crumb Shop is ${\sum }_n\left(V_h\right(n+1)-V_h(n\left)\right)\cdot P_N\left(n\right)$ ^[5][6]. This leads to a much more sensible output, and the new estimate looks like this.

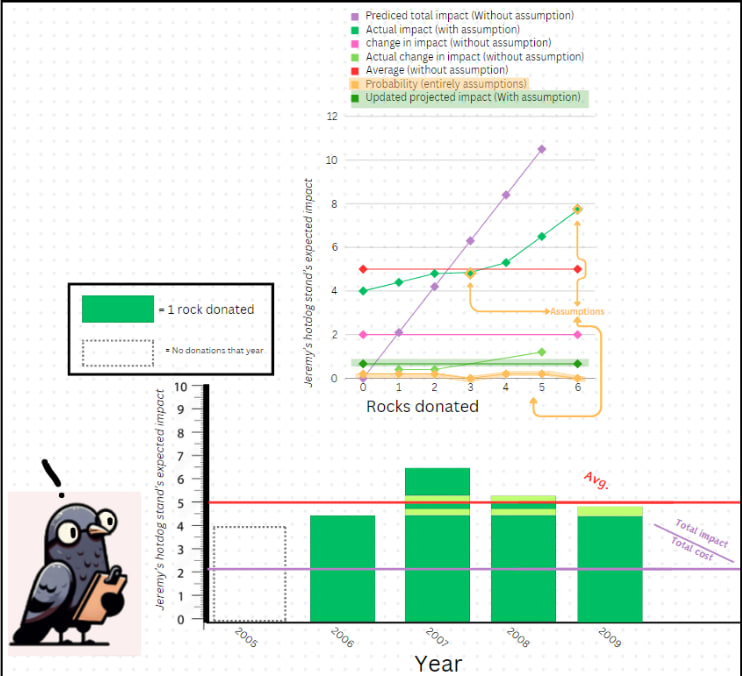
After making some assumptions, he calculated his new estimate like this. 

Calculations (Feel free to skip this part)

${\sum }_n\left(V_h\right(n+1)-V_h(n\left)\right)\cdot P_N\left(n\right)$

$=\left(V_h\right(0+1)-V_h(0\left)\right)\cdot P_N\left(0\right)$

$+\left(V_h\right(1+1)-V_h(1\left)\right)\cdot P_N\left(1\right)$

$+\left(V_h\right(2+1)-V_h(2\left)\right)\cdot P_N\left(2\right)$

$+\left(V_h\right(3+1)-V_h(3\left)\right)\cdot P_N\left(3\right)$

$+\left(V_h\right(4+1)-V_h(4\left)\right)\cdot P_N\left(4\right)$

$+\left(V_h\right(5+1)-V_h(5\left)\right)\cdot P_N\left(5\right)$

$=(4.4-4)\cdot \frac{1}{5}$

$+(4.8-4.4)\cdot \frac{1}{5}$

$+(4.85$^[7]$-4.8)\cdot \frac{1}{5}$

$+(5.3-4.85$^[7]$)\cdot 0$

$+(6.5-5.3)\cdot \frac{1}{5}$

+$(7.7$^[7]$-6.5)\cdot \frac{1}{5}$ 

$=\left[\right(0.4)\cdot \frac{1}{5}]+\left[\right(0.4)\cdot \frac{1}{5}]+\left[\right(0.05)\cdot \frac{1}{5}]+\left[\right(0.45)\cdot 0]+\left[\right(1.2)\cdot \frac{1}{5}]+\left[\right(1.2)\cdot \frac{1}{5}]$

$=0.66$.

Findings

This is a much better result. He did make some assumptions, but the assumptions he made don't seem too unreasonable, so he's happy with his results.

Note that you can intuitively think of the change in the value of a (where a is the expected impact of Jeremy's Flavored Crumb Shop) when we shift the probabilities to the left by one.

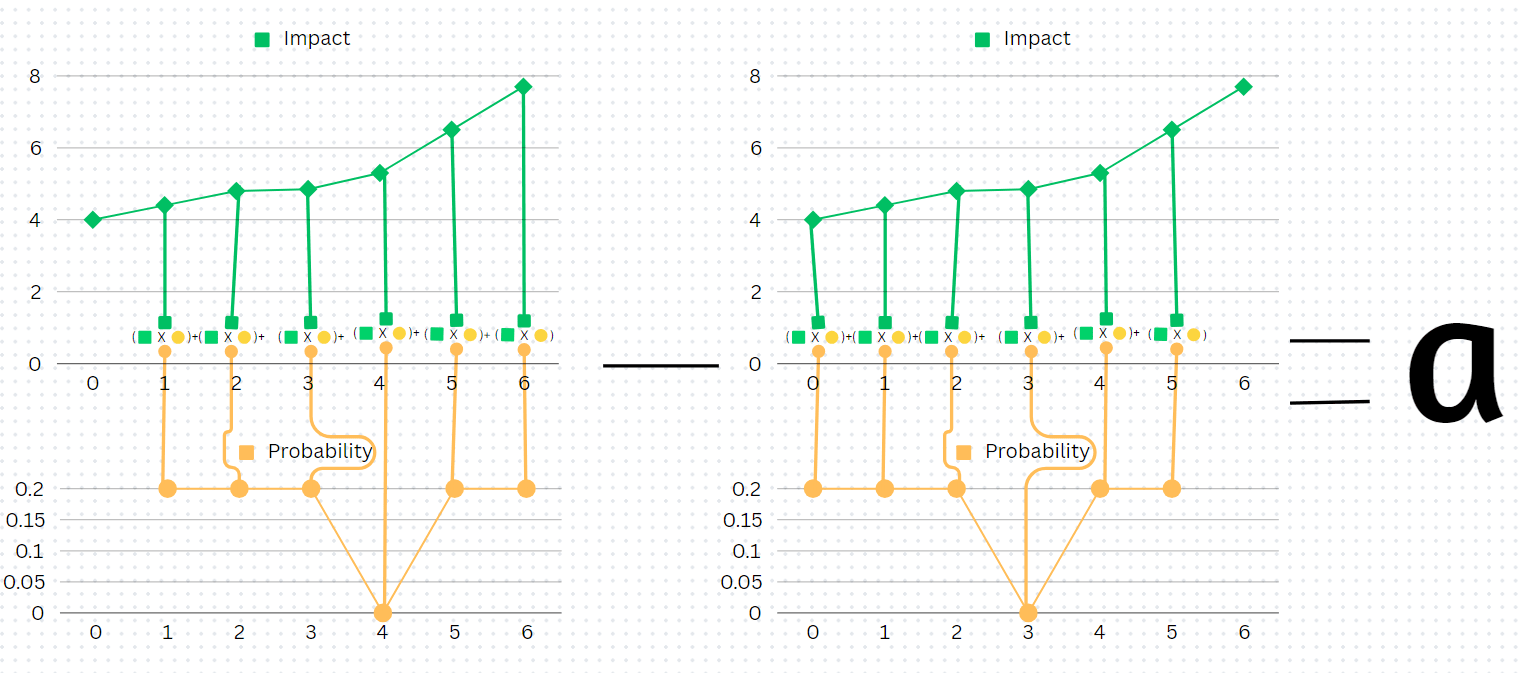
What about if the expected value of [donating twice as much] is twice as big?

First of all, note how we can express the impact of donating one rock to Jeremy's Hotdog Shop as $E\left(V_h\right(N+1)-(V_h\left(N\right))$. Similarly, we can express $a$ rocks donated as $E\left(V_h\right(N+a)-(V_h\left(N\right)).$ Now, we just need to know if $E\left(V_h\right(N+a)-(V_h\left(N\right))=a\cdot E(V_h(N+1)-\left(V_h\right(N\left)\right).$ But, it turns out that this is not the case. To show why this is true, consider the following example.

$V_h\left(1\right)=1,V_h\left(2\right)=1,V_h\left(3\right)=3,$ and $P_N\left(1\right)=1.$ Therefore,

1. $E\left(V_h\right(N+1)-(V_h\left(N\right))=0$, since N can only be 1, $V_h(1+1)=1,and{V}_h\left(1\right)=1$.
2. $E\left(V_h\right(N+2)-(V_h\left(N\right))=2$, since N can only be 1, $V_h(1+2)=3,and{V}_h\left(1\right)=1$.
3. $0\cdot 2\ne 2$.
4. $a=2.$
5. $E\left(V_h\right(N+2)-(V_h\left(N\right))\ne 2\cdot E(V_h(N+1)-\left(V_h\right(N\left)\right).$
6. $E\left(V_h\right(N+a)-(V_h\left(N\right))\ne a\cdot E(V_h(N+1)-\left(V_h\right(N\left)\right).$

Despite this, on average, $E\left(V_h\right(N+a)-(V_h\left(N\right))=a\cdot E(V_h(N+1)-\left(V_h\right(N\left)\right)$, since, on average, data is linear (i.e. $E\left(f^{\prime \prime }\right(x\left)\right)=0$, since $f^{\prime \prime }\left(x\right)=h\left(x\right),$ and $E\left(h\right(x\left)\right)$(i.e., data is neither skewed to the more negative side nor the more positive side)(i.e., graphs of data are, on average, in the shape of a line) and when $f\left(x\right)$ is linear, by definition,  for all  $f\left(x\right)$, $f\left(x\right)=mx+b$, with some $m$ and $b$. 

Furthermore, for all $f\left(x\right)$, where $f\left(x\right)=mx+b$, for all x,$f(x+a)-f\left(x\right)=\left(m\right(x+a)+b)-(mx+b)$

$=\left(\right(mx+ma)+b)-(mx+b)=mx+ma+b-mx-b=ma.$

Therefore, for all linear functions $f\left(x\right)$, $a\left(f\right(x+1)-f(x\left)\right)=f(x+a)-f\left(x\right),$ since$f(x+1)-f\left(x\right)=m$, $m\cdot a=ma$, and $f(x+a)-f\left(x\right)=ma$.

It's important to note that, while on average, $E\left(V_h\right(N+a)-(V_h\left(N\right))=a\cdot E(V_h(N+1)-\left(V_h\right(N\left)\right)$ holds, when V_h(x) isn't linear,   $a\cdot E\left(V_h\right(N+1)-(V_h\left(N\right))$ isn't a perfect estimate for $E\left(V_h\right(N+a)-(V_h\left(N\right)).$

Sidenote

Similarly, $\frac{effectiveness}{cost}$ is a decent approximation for cost-effectiveness, as, given the way most charities operate, the impact of each "rock" donated is roughly independent of the charity's total money that would have been donated if said "rock" was not donated. (i.e., if you were to graph impact as the y-axis and the number of dollars donated, the shape that would form would look like a line).

All functions that make this line shape can, by definition, be written in the form $y=mx+b$, where:

1.  $x$is the total amount of donated "rocks" is $x$.
2. The impact is $y$.
3.  $m$ can be thought of as "Impact per rock."
4.  $b$ can be thought of as "impact that the charity did regardless of donations (e.g. if the co-founders were nice to their parents regardless of that year's donations). We want to know "impact per rock."

Therefore, $\frac{y}{x}=m+\frac{b}{x}$, and what we want to know is $m$, and, as $x$ gets larger and larger, $m+\frac{b}{x}$ trends towards $m$ , since$\frac{b}{x}$ trends towards $0$.

Congrats! You made it to the end of this article! 🥳!

Now, Todd can finally sit, having finished all his winter break homework. ^[8]

(also, I wanted to make a picture of Todd eating a crumb, but this picture of Todd eating a hotdog turned out way cuter. 🐦‍⬛🌭 )

If you have any questions, comments, suggestions, corrections, or feedback, please feel free to put them in the comments!

1. ^{^}

   The Avg. is short for the average (Arithmetic mean) yearly impact.

2. ^{^}

   where E(x) is the expected value of x, N is the number of rocks Jeremy's Hotdog Stand gets in any given year, and $V_h\left(N\right)$ is the value generated by Jeremy's Hotdog Stand when Jeremy's Hotdog Stand gets N rocks.

3. ^{^}

   $P_X\left(x\right)$ is the probability that some random variable X is equal to $x$.

^{^}



 

^{^}

We can see why this is true if we input $X=V_h(N+1)-\left(V_h\right(N)$.

^{^}

When $V_h\left(some\mathrm{number}\right)$ is known, but $V_h(some\mathrm{number}+1)$ isn't known, use some estimation for $V_h(some\mathrm{number}+1)$. (e.g., $V_h\left(some\mathrm{number}\right)+0.375)$.   The same goes for when $P_N\left(n\right)$ is unknown. (That is, we estimate $P_N\left(n\right)$)

^{^}

Todd assumed that $P_N\left(0\right)=\frac{1}{5},P_N\left(1\right)=\frac{1}{5},P_N\left(2\right)=\frac{1}{5},P_N\left(4\right)=\frac{1}{5},P_N\left(5\right)=\frac{1}{5},V_h\left(3\right)=4.85,\mathrm{and}{V}_h\left(6\right)=7.7.$

^{^}

I imagine that pigeons get only one piece of homework for winter break.

Show all footnotes