Stan Pinsent
Bio
Participation3
Views my own.
Posts 26
Comments115
Topic contributions1
Influence of smaller parties is growing: Even without winning an election, third parties could achieve higher vote share, stronger media presence, and policy influence
I'd go further and say that a coalition government is much more likely when the small parties gain MPs, and that a small party in a coalition could have a lot of power.
I don't think any party would join a coalition with Reform, however. Lib Dems could feasibly join a coalition with Labour or the Conservatives.
[Update: the tool does capture diminishing marginal cost-effectiveness - see reply]
Cool tool!
I'd be interested to see how it performs if each project has diminishing marginal cost-effectiveness - presumably there would be a lot more diversification. As it stands, it seems better suited to individual decision-making.
Hi Mike, thanks for taking the time to respond to another of my posts.
I think we might broadly agree on the main takeaway here, which is something like people should not assume that nuclear winter is proven - there are important uncertainties.
The rest is wrangling over details, which is important work but not essential reading for most people.
Comparing the estimates, the main cause of the differences in soot injection are if firestorms will form. Conditional on firestorms forming, my read of the literature is that at least significant lofting is likely to occur - this isn’t just from Rutgers.
Yes, I agree that the crux is whether firestorms will form. The difficulty is that we can only rely on very limited observations from Hiroshima and Nagasaki, plus modeling by various teams that may have political agendas.
I considered not modeling the detonation-soot relationship as a distribution, because the most important distinction is binary - would a modern-day countervalue nuclear exchange trigger firestorms? Unfortunately I could not figure out a way of converting the evidence base into a fair weighting of 'yes' vs. 'no', and the distributional approach I take is inevitably highly subjective.
Another approach I could have taken is modeling as a distribution the answer to the question "how specific do conditions have to be for firestorms to form?". We know that a firestorm did form in a dense, wooden city hit by a small fission weapon in summer, with low winds. Firestorms are possible, but it is unclear how likely they are.
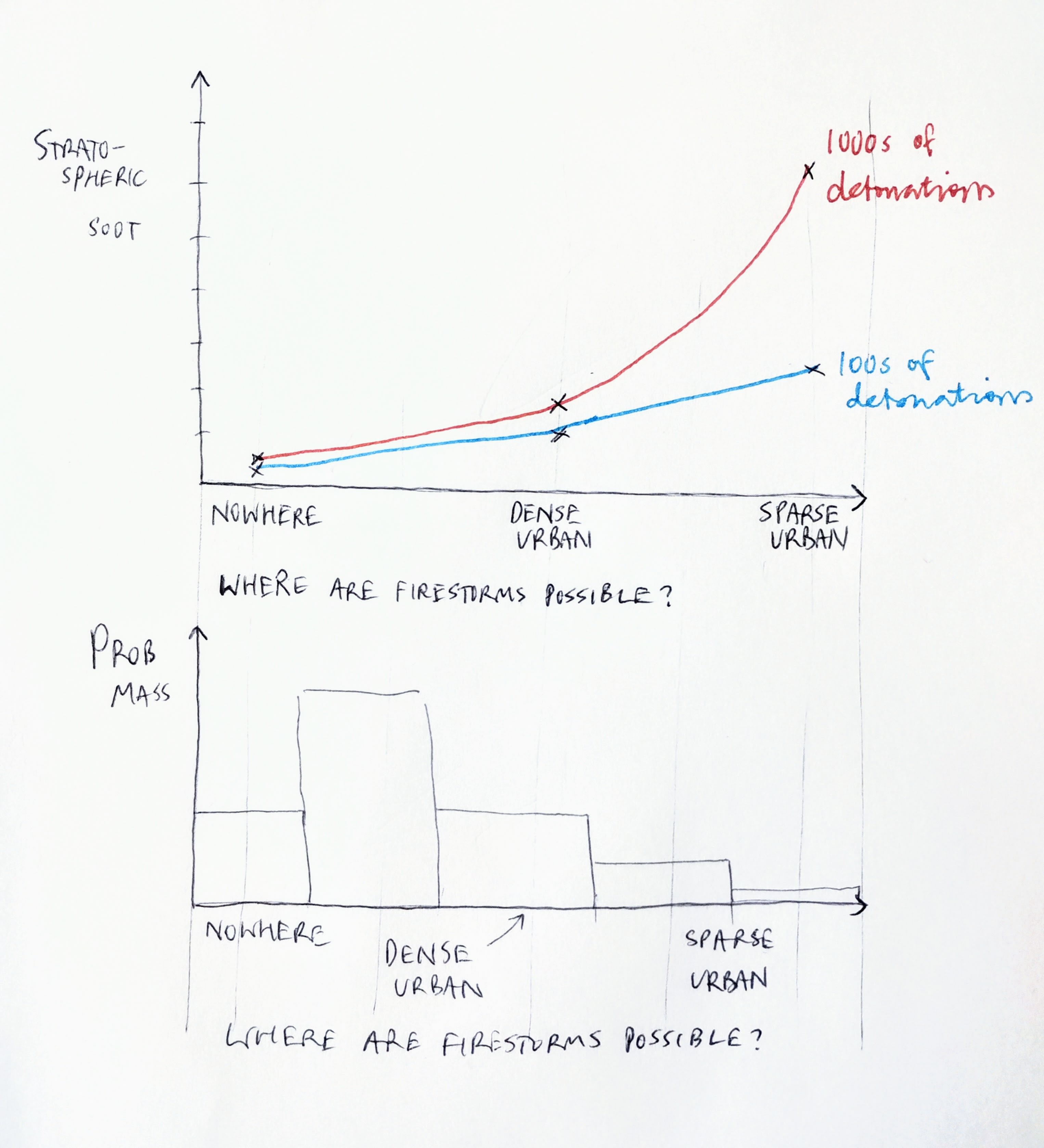
These charts are made up. The lower chart is an approximation of what my approach implies about firestorm conditions: most likely, firestorms are possible but relatively rare.
Los Alamos and Rutgers are not very helpful in forming this distribution: Los Alamos claim that firestorms are not possible anywhere. Rutgers claims that they are possible in dense cities under specific atmospheric conditions (and perhaps elsewhere). This gives us little to go on.
Fusion (Thermonuclear) weaponry is often at least an order of magnitude larger than the atomic bomb dropped on Hiroshima. This may well raise the probability of firestorms, although this is not easy to determine definitively.
Agreed. My understanding is that fusion weapons are not qualitatively different in any important way other than power.
Yet there is a lot of uncertainty - it has been proposed that large blast waves could smother much of the flammable materials with concrete rubble in modern cities. The height at which weapons are detonated also alters the effects of radiative heat vs blast, etc.
you only need maybe 100 or so firestorms to cause a serious nuclear winter. This may not be a high bar to reach with so many weapons in play.
Semi agree. Rutgers model the effects of a 100+ detonation conflict between India and Pakistan:
- They find 1-2 degree cooling over cropland at the peak of the catastrophe. This would be unprecedented and really bad, but not serious compared to the nuclear winter we have in our imagination: I estimate about 100x less bad than the doomsday scenario with 10+ degrees cooling.
- They are modeling 100 small fission weapons, so it would be worse with large weapons, or more detonations. But not as much worse as you might think: the 51st detonation is maybe 2-5x less damaging than the 5th.
- Furthermore, they are assuming that each side targets for maximum firestorm damage. They assume that fuel loading is proportional to population density, and India & Pakistan have some of the world's densest cities. So this is almost the worst damage you could do with 100 detonations.
- Although 100 detonations sounds very small, this idealized conflict would be tapping into most of the firestorm potential of two countries in which 20% of the world's population live - much more than live in the US and Russia.
- It's possible that 100 firestorms could trigger measurable cooling, but the conditions would have to be quite specific. 1000 firestorms seems much less likely still.
Conclusion
In the post I suggest that nuclear winter proponents may be guilty of inflating cooling effects by compounding a series of small exaggerations. I may be guilty of the same thing in the opposite direction!
I don't see my model as a major step forward for the field of nuclear winter. It borrows results from proper climate models. But it is bolder than many other models, extending to annual risk and expected damage. And, unlike the papers which explore only the worst-case, it accounts for important factors like countervalue/force targeting and the number of detonations. I find that nuclear autumn is at least as great a threat as nuclear winter, with important implications for resilience-building.
The main thing I would like people to take away is that we remain uncertain what would be more damaging about a nuclear conflict: the direct destruction, or its climate-cooling effects.
I wonder whether it is worth for me to invest significant time in writing comments like mine above. It seems that they are often downvoted, and that I can sometimes tell before hand when this is going to be case. So, to the extent karma is a good proxy for what people value, I wonder whether I am just spending signicant time on doing something which has little value.
I am sad to see your comment getting downvotes as I do think it contributes a lot of value to the discussion.
I can guess why you might be getting them. You often respond to cause-prio posts with "what about corporate campaigns for chicken welfare?", and many people now probably switch off and downvote when they see this. Maybe just keep the chicken comparison to one line and link to your original post/comment?
Also, you comment is 3200 words long - about 3x longer than the actual post. I think a 200-word summary-of-the-comment with bullet points would be really useful for readers who have only read this post and are unable to pick up the finer points of your modeling critique.
On animal welfare
- I think that if you adopt RP's moral weight estimates and reject speciesism, it is almost inevitable that the most cost-effective interventions to improve wellbeing will be animal welfare interventions.
- My understanding is that CEARCH is not against evaluating animal welfare interventions in principle, but in practice we are not doing so while comparisons between human and animal welfare remain so shaky. Our research direction is also partly driven by the value of information, ie. how much resources we can plausibly redirect and the impact this will have. Maybe this is too deterministic of me, but I feel that banging the drum about corporate chicken campaigns will only open so many wallets.
Hi Mike,
Firstly, thanks to you and all of ALLFED for your willingness to let me prod and poke at your work in the past year.
You make some excellent points and I think they will help readers to decide where they stand on the important cruxes here.
We assign a higher probability that a nuclear conflict occurs compared to your estimates, and also assume that conditional on a nuclear conflict occurring that higher detonation totals are likely. This raises the likelihood and severity of nuclear winters versus your estimates.
For anyone wanting to get up to speed on my nuclear winter model, plus a quick intro to why nuclear cooling is so uncertain, see my just-released nuclear winter post.
- Weightings of Metaculus, XPT vs individual estimates: we do place high weightings on individual's estimates, which is not ideal. The main reason for this is that the Metaculus and XPT estimates are not calibrated to a 100+ detonation nuclear conflict involving US and/or Russia.
- The Metaculus estimate still forms around 20% of the total weight. Overall, it seems credible that my final estimate (0.10%) is around a third of the Metaculus estimate (0.30%) for 100+ detonations, given that most experts I spoke to considered India/Pakistan to be one of the main threats of a 100+ detonation nuclear exchange.
- The XPT estimate only forms around 2% of the total weight.
- Distribution of the number of detonations in a 100+ detonation conflict. I have done my best to incorporate different sources of evidence. One expert I spoke to broadly agreed with you, Mike, and guessed that in a 100+ conflict involving US/Russia there would be 80-90% risk of over 1000 detonations. Another expert was less pessimistic and placed higher weight on the possibility of 'moderate' escalation involving hundreds of weapons.
- I re-ran the numbers just looking at conflicts with over 1000 detonations and found that the cooling levels increase only modestly: the 75th-percentile cooling level increases from 0.66 degrees (100+ detonations) to 1.24 degrees (1000+ detonations). The initial assumption about soot volumes is far more important (see below)
- Detonation-soot relationship: Yes, the results are extremely sensitive to the initial assumption about how much soot is produced in a small nuclear exchange targeting cities. When I re-ran the numbers under the more pessimistic assumption that soot levels were 10%-100% those predicted by Toon et al., 75th-percentile cooling increased from 0.66 degrees to 3 degrees.
We estimate that the expected mortality from supervolcanic eruptions (VEI 8+) would be comparable to VEI 7 eruptions, so their inclusion could increase cost effectiveness significantly.
I don't exclude supereruptions; I estimate that the right tail of my volcanic cooling model already accounts for them.
We feel that you are selling short the importance of research in building resilience to nuclear winters in particular and ASRSs in general [...] Overall, we see research as the foundation on which you then build the policy work and other actions. Broadening and strengthening this foundation is therefore vital in allowing the work that finally effects change to occur - it isn’t an either/or.
I want to be clear that I recommend that funders prioritize policy advocacy over R&D on the margin at this point in time. I totally agree that advocacy on such an uncertain topic can only be effective if it is grounded in research, and that ALLFED's research will very likely form the foundations of policy work in this area for years to come.
One key takeaway from my analysis is that mild and moderate scenarios form a larger proportion of the threat than the lore of nuclear winter might suggest. Resilient foods would likely have a role to play in these scenarios, but I think the calories at stake in distribution and adaptation are likely to be more pivotal.
One reason for my focus on resilient food pilot studies is that they are a possible next step for ALLFED if it were to receive a funding boost. ALLFED has been ticking along with modest but reliable core funding for some time now, and perhaps I am guilty of taking its theoretical research for granted.
Feel free to set the record straight and give some indication of the kinds of work ALLFED might be interested in accepting funding for.
Good point.
I looked at WTO agreements early in the research process and eventually decided that WTO advocacy was probably not, on the margin, the best way forward.
Food stockholding
I focused on the consequences of the AoA for food stockpiling (known as "stockholding"), the most urgent concern being that it may dissuade countries from stockholding as much as they otherwise would (as suggested by Adin Richards here). Although food reserves would never be big enough to get us through a full catastrophe, they would buy time for countries to adapt to the cooling shock.
The feedback I got from someone with experience at the WTO since the 1990's was
- The AoA probably isn't holding countries back from stockholding. It does not make any restrictions on how much a country can hold, only on how much a country can spend on subsidizing domestically-produced stocks [while technically true, a lot of authors certainly seem to believe that the AoA affects stockholding, eg. here].
- This AoA appears to be counterfactually reducing subsidies for only a handful of products in a few countries. India is the only country to have notified exceeding its limit, and only for rice.
- The AoA seems intractable. The G33, a coalition of LMICs, have pushed for change with no success
On the other hand, basic amendment to the AoA seems obviously needed (imho). The original agreement does not properly allow for inflation. It does not make adequate exceptions for very low-income countries (whose market share is so low that allowing them to subsidize farmers would not be very distortionary).
Overall the WTO seems deadlocked at the moment and suffering a crisis of legitimacy. Tit-for-tat between US and China has led to a breakdown of trust in the organization.
If the US was on-side for AoA amendment, it is possible that the other dissenting countries would fall in line. But it is not clear that the US can be influenced on this. The US is doing fine with the system as it currently is, and has other ways of subsidizing domestic agriculture.
Other WTO theories of change
I don't know much about the implications of the AoA beyond stockholding.
The most important things is that we ensure trade continues in a catastrophe, which seems congruent with the AoA. The second most important thing is that countries are able to quickly adapt their food systems in a crisis. In a major catastrophe I think all WTO rules would go out of the window. But could the AoA prevent countries from preparing?
- It may hold them back from stockholding, or producing much more food than the market demands. But these measures would likely be way too expensive for governments to support in the name of preparing for a 1-in-400 event, anyway.
- It may prevent them from using agri subsidies to foster emerging, resilient food sources that are not economically viable in normal times. But these food sources are at an early stage of development - pilot studies at most - and my guess is that they could be pursued under academic or innovation budgets.
I may well be missing something. Are there other ways the AoA could frustrate resilience work?
Hi Vasco. Thanks for all of your help giving feedback on the report and the modeling underpinning the CEA.
I am going to focus on the main points that you make. I hope to explain why I chose not to adopt the changes you mention in your comment and also to highlight some key weaknesses and limitations of my model.
Points I address (paraphrasing what you said):
- By asking domain experts you probably got an overestimate for "probability that advocacy succeeds". You should have also asked people in other fields.
- Although you mention fungibility, you don't account for it in cost-effectiveness estimates. You should be more explicit that fungibility undermines cost-effectiveness of grants that perform other, less effective interventions.
- You overestimate the mortality effects of mild cooling events: if we apply your model to the 1815 eruption, we get higher mortality rates than actually occurred.
- Poverty is a strong predictor of famine mortality. If your persistence estimate relied only on poverty & malnutrition burden indicators, the full-term benefits of policy advocacy would be significantly lower
By asking domain experts you probably got an overestimate for "probability that advocacy succeeds". You should have also asked people in other fields.
- I agree that domain experts are likely to overestimate the probability of successful policy advocacy in their space.
- In my defence, only two of the seven experts I consulted for estimates worked in food resilience specifically. The geometric mean of their estimates was 30%; only slightly higher than the group average of 24%. The other experts would be best classified as GCR experts (so still likely to be overly optimistic)
- The difficulty is that people who are not domain experts are (by definition) not well-informed. I don't think people at GiveWell will have an accurate understanding of prospects for ASRS resilience policy advocacy. Especially because this is a very small field.
Although you mention fungibility, you don't account for it in cost-effectiveness estimates. You should be more explicit that fungibility undermines cost-effectiveness of grants that perform other, less effective interventions.
I think that in ideal circumstances, fungibility should be accounted for in cost-effectiveness analysis. But since it depends on the organization receiving the funding, I decided not to do quantitative estimates of fungibility effects in this report. Maybe we will do so when we evaluate specific grants in this area.
I agree that funding to orgs who only do one highly cost-effective thing is generally less fungible.
You overestimate the mortality effects of mild cooling events: if we apply your model to the 1815 eruption, we get higher mortality rates than actually occurred.
I love this analysis, thanks for doing it.
First, let me say that yes, my model is very sensitive to mortality estimates in mild cooling scenarios. My estimate may be too high, but I believe there are compelling reasons not to be confident of this.
To illustrate my model for mortality in a mild cooling event (1-2.65 degrees cooling):
- 2% probability of 6% mortality (no adaptation, no food trade)
- 18% probability of 3% mortality (no food trade)
- 80% probability of no mortality
- This gives an average of approximately 0.6% mortality
My counterarguments are as follows:
- On a broad level, I think that a 'panic' scenario could include countries banning food exports to secure domestic supplies. This would be catastrophic for some food-importing countries even in normal climate conditions. The same cannot be said for the world of 1815, where almost all food was consumed locally and very few people lived far from agricultural areas.
- I think the comparison with 1815 is well worth doing. However, there are a number of reasons why the validity of the comparison is limited:
- A global 1% mortality event in 1815 may not have even been noticed. We have to patch together estimates of famine mortality in 1815 because there was almost no systematic documentation at the time. People were not aware of any global phenomenon, so nobody was trying to "join up the dots" and tally the full famine impact that year. Especially if much of the effects were felt in South Asia, East Asia or Africa, it is possible that a major-yet-distributed famine could have gone unnoticed
- Relatively few people in the world of 1815 relied on food imports, as mentioned above[1]. Breakdown in international food trade is the main famine mechanism in modern-day agricultural catastrophes, but it barely applies to the agrarian economies of 1815.
- Local famine effects may not have been worse in Indonesia. Undoubtedly, the effects of ash blanketing crops would have been worse near the eruption. But stratospheric soot quickly circulates around the world. Furthermore, Indonesia has a warm climate and would not have been at risk from completely failed harvests through unseasonal frost. Multiple annual harvests are common in the tropics; in higher latitudes, a failed crop leaves farmers without food for almost a year.
- Cooling damage is highly superlinear. The Pinatubo eruption of 1991 caused 0.5 degrees of cooling and is not associated with important declines in agricultural productivity. Thus we might expect the expected burden of an 1815-level cooling event (0.8 to 1.3 degrees cooling) to be far lower than a 1-2.65 degree cooling event[2].
Poverty is a strong predictor of famine mortality. If your persistence estimate relied only on poverty & malnutrition burden indicators, the full-term benefits of policy advocacy would be significantly lower.
To push back:
- A world with no extreme poverty and no nutritional diseases would still be vulnerable to global agricultural catastrophes. The advantage of my "grain production per capita" metric is that it has no such edge-case problems: more grain is always good for food security.
- The famine/poverty relationship is strong in normal times. There are a number of reasons that it may become less strong in an agricultural catastrophe
- Many of the global poor are subsistence farmers in warm countries. This demographic will be close to food supplies and away from the risk of frosts etc.. They may be better-positioned to survive than their middle-class compatriots in cities.
- People at the bottom of the pile are the most at-risk of post-catastrophe famine, regardless of whether they are in absolute poverty. A wealthier world would simply have higher food prices, leaving the poorest without enough to eat.
- As described above, the main cause of famine in my model is the breakdown of food trade. It is not clear that progress against poverty and nutritional diseases is an indication that populations are less dependent on food trade. If anything, development is probably associated with increased reliance on trade.
Thanks again for the detailed feedback!!
- ^
Admittedly, this would have made some people more vulnerable as it was difficult to relieve famine-stricken areas.
- ^
A counterargument could be that Western Europe appears to have had particularly bad summer cooling in 1816 - as well as better record-keeping than much of the world - and their famines were not so bad. On the other hand, spring cooling may be more important, as late frosts can ruin harvests of wheat, potatoes etc.

Yep, you've convinced me. I asked a friend in politics and they were very confident that if push came to shove, the Tories would share power with Reform. I think I didn't consider the alternative: Reform joining forces with a Leftwing party, or a lack of any formal coalition.