In this fictional dialogue between a Bayesian (B) and a Non-believer (N) I will propose solutions to some pre-existing problems with Bayesian epistemology, as well as introduce a new problem for which I offer a solution at the end. (Computer scientists may consider skipping to that section).
Here’s a Bayes theorem cheat sheet if you need it:

The problem of confirmation
Nayesian: Remind me again, how does confirmation work in Bayesianism?
Bayesian: The evidence E confirms hypothesis H if and only if the posterior probability of H given E is greater than the prior probability of H.
N: So there is no difference between increasing the hypothesis’ probability and confirming a hypothesis?
B: Not really, no.
N: I would say that there are cases where something increases the probability of a hypothesis, but we would not say that it confirms the hypothesis. Let's say there is a recent hypothesis that has a strong theoretical foundation and some evidence from a few experiments. Scientists disagree about whether or not this hypothesis is correct. But, again, it's a novel proposal. Say that a recent article published in a highly regarded scientific journal supports this hypothesis. Appearing in the journal increases my degree of belief that the hypothesis is true. So it appears that the Bayesian must conclude that a publication in a reputable scientific journal confirms the hypothesis, but surely that is incorrect. Appearing in a reputable scientific journal isn't in and of itself evidence that a hypothesis is correct; it merely implies that there exists evidence supporting the hypothesis.
B: No, I would say that appearing in a scientific journal is evidence, although maybe a different type of evidence than we would normally associate with that word. Perhaps we should make a taxonomy of evidence so we don’t end up in information cascades.
N: Weird. What about the other way around? What if there’s a fact that confirms a hypothesis without increasing its probability?
B: Can you give an example?
N: Sure! Let’s say I throw a rock at someone and use Newtonian mechanics to calculate the trajectory of the rock. The predicted trajectory indeed happens, but that doesn’t increase my credence in Newtonian mechanics since I believe that general relativity has displaced it. If we know Newtonian mechanics is false, its probability is zero, and that probability will never increase regardless of how many correct predictions it makes.
B: So? That seems reasonable to me. A falsified theory remains falsified even if it makes a correct prediction.
N: But surely the theory of Newtonian mechanics is less wrong than, I don’t know, the existence of fairies that make square circles. We want to be able to say that theories that make loads of correct predictions are better than those that don’t, and that the people in the past who believed in Newtonian mechanics were reasonable while those who believed in square-circle-making fairies weren’t. The first group used evidence to support their hypothesis, while the second group didn’t.
B: I don’t think you can use Bayesianism retroactively like that.
N: It’s not just a problem for retroactive evaluations. Many modern scientific theories and models include idealizations, in which certain properties of a system are intentionally simplified. For example, in physics, we often use the ideal gas law. An ideal gas consists of dimensionless particles whose movements are completely random. But an ideal gas doesn’t exist; we invented the concept to decrease the complexity of our computations. We know that the actual probability of theories that use the ideal gas law is 0. Under Bayesianism, any and all theories that make use of the ideal gas law would have no way to increase their probability. Yet we continue to believe that new evidence confirms these models, and it seems rational to do so.
B: Okay, I guess I’ll have to actually make this taxonomy of evidence now. Let’s call the evidence provided by being published in a scientific journal "secondhand evidence". What we want is "firsthand evidence". Personal confirmation might come from secondhand evidence, but the only way to confirm a hypothesis in the conventional sense of the word is to do primary research. Do experiments, try to falsify it etc. When a hypothesis appears in a scientific journal, it is not a test of the hypothesis; rather, the paper in the journal simply reports on previous research. It’s secondhand evidence.
N: I mean, it’s a kind of "test" whether or not a theory can even make it into a journal.
B: But it’s not a scientific test. Similarly, we can obviously set up tests of hypotheses we know are false, including models with idealizations. We can, for example, use a false hypothesis to design an experiment and predict a specific set of outcomes.
N: Seems vague. You would need to find a way to differentiate secondhand evidence from firsthand evidence and then design different ways Bayesianism deals with both types of evidence.
B: I’ll get right on it!
The problem of old evidence
BaNo: I think Bayesianism struggles with retrodiction.[1]
BaYes: Why do you think so?
N: Well, consider the following scenario: scientists can’t explain why volcanoes erupted when they did. We’ll call this piece of evidence (the pattern of eruptions) E. Then a new volcanological theory comes out that retrodicts the timing of all eruptions to the second. It seems like the fact that this theory can perfectly explain the timing of the eruptions is evidence that said theory is correct.
However, Bayesianism says that E confirms H when H’s posterior given E is higher than H’s prior, and we work out the posterior by applying Bayes’ rule. At the time the new theory was proposed, the pattern of the eruptions was already known, so the probability of E equals 1.
Which means the probability of E given H is also 1. It then follows that the probability of H given E is equal to the probability of H, so the posterior is equal to the prior. In other words: E can't confirm H when E is already known.
Under Bayesianism, no matter how impressive of a retrodiction a theory makes, it can never strengthen that theory.
B: I mean, what if I just give theories that provide good retrodictions a higher prior?
N: That wouldn’t work in scenarios where we only discover the retrodiction after the theory has already been introduced. If I propose this new volcanological theory and we assign it a prior and only later we discover its perfect retrodiction, the prior has already been assigned.
B: What if we used a counterfactual? Instead of asking ourselves what the scientist’s actual degree of belief is in E we ask ourselves what her degree of belief would have been had she not known about E. In that case, the probability of E does not just equal 1.
N: How do we know what her degree of belief would have been?
B: Well, say she forgets all the volcanic eruptions without it altering her other knowledge.
N: Impossible, knowledge is entangled with one another, especially something as drastic and traumatic as volcanic eruptions.
B: Okay okay, what about a counterfactual history instead, where no one knows about volcanic eruptions and we ask the scientific community in this timeline what they think.
N: And these scientists don’t know about volcanic eruptions? What, do they live on Mars or something? How are we supposed to know what alternate universe alien scientists believe?
B: Alright, alright, I’ll bite the bullet, retrodictions don’t strengthen a theory.
N: But this is not only a problem for retrodictions, but also for old predictions. Say a theory made a correct prediction. E.g. germ theory predicted that if we looked under a microscope we would see microbes. Then when the modern microscope was invented it turned out to be a correct prediction. But we live in the present, and for us the fact that looking into a microscope will show us microbes is not new evidence. For us it’s probability is one. So, according to Bayesianism, when we first learn of germ theory, the fact that we know that we can look into a microscope to see germs can’t confirm germ theory. That’s ridiculous!
B: I think I can combine a solution for the problem of retrodiction with the problem of confirmation. The problem of us wanting to update on the ‘secondhand evidence’ of appearing in a scientific journal seems analogous to germ theory correctly predicting microbes in the past, and us ‘wanting’ to update on that past successful prediction.
What if we considered a kind of ‘collective Bayesianism’ which describes what an interconnected collection of agents (ought to) update towards. A ‘Bayesian collective’ does update because of germ theory’s successful prediction, since it’s around for that. At this point it becomes easy to make that distinction between ‘firsthand evidence’ and ‘secondhand evidence’. ‘Firsthand evidence’ is that which makes the Bayesian collective and the Bayesian individual update, whereas ‘secondhand evidence’ only makes the individual Bayesian update.
For you as an individual it’s a surprise that something has appeared in a scientific journal and ‘confirms’ a theory, but it doesn’t for the collective. The goal of the Bayesian individual is not only to use ‘firsthand evidence’ to update the knowledgebase of themself (and the collective), but also to use ‘secondhand evidence’ to bring their own credences as much in line with the Bayesian collective as possible.
N: So would an alien scientist be part of our Bayesian collective?
B: It must be interconnected, so if it can’t communicate with us, no.
N: In this model, if a historian discovers a long lost text from ancient Greece they aren’t collecting firsthand evidence? The collective doesn’t update?
B: Bayesianism is an epistemic ideal to strive towards, not a description of how people actually work. An actual collective will not conform to how the ideal of a Bayesian collective operates. An ideal Bayesian collective doesn’t forget anything, but obviously real people and groups do forget things. An ideal Bayesian collective wouldn’t need historians, the insights from ancient greek writers would continue to be in the network, and the collective thus wouldn’t update on the ancient greek text. But real collectives do need historians, and they do update on the ancient greek text, because mankind keeps forgetting it’s history.[2]
The problem of logical omniscience
Bay=cray: What are the axioms of probability theory again?
Bay=bae: They are:
- Axiom 1: The probability of an event is a real number greater than or equal to 0 and smaller than or equal to 1.
- Axiom 2: The probability that at least one of all the possible outcomes of a process (such as rolling a die) will occur is 1.
- Axiom 3: If two events A and B are mutually exclusive, then the probability of either A or B occurring is the probability of A occurring plus the probability of B occurring.
N: And Bayesianism treats the axioms of probability theory as constraints on one's degrees of belief. In other words, for the Bayesian, probabilities are the same as degrees of belief, right?
B: Correct.
N: How do we know what our degrees of beliefs are?
B: With bets. If you think the odds of Biden being reelected is one in three, the most risky odds you would take for a bet on that outcome is one in three.
N: I don’t know, it seems like degrees of belief and probability are dissimilar in many ways. We have all sorts of biases, like base rate neglect, that make our beliefs different from what a Bayesian would prescribe.
B: Yes, just like with the memory issue, Bayesianism is not a descriptive model of how humans form beliefs, it is a prescriptive model of what humans ought to believe. Treat it as a goal to strive towards.
N: Okay, but what about mathematical truths? The statement 4 = 4 is true by definition. So, according to the axioms of probability theory, it should have a probability of 1, since logical truths are necessarily true. But there are many logical truths about which we are uncertain. Just think of all of the currently unproven mathematical conjectures. Do you think P=NP is true? False? Are you unsure? I doubt most people would say they are 100% confident either way. But logically these conjectures are either necessarily true or necessarily false. So they should all have a probability of either 0 or 1.
This becomes especially problematic when you think about how Bayesianism tells me I should be willing to take bets based on a theory’s probability. The probability of Pythagoras’ theorem is 1, but I’m not willing to bet all my money on it without someone else putting money in too. I can believe that the probability of a mathematical theorem or conjecture is 1, without being certain that it is true.
Bayesianism seems to have trouble explaining doubts about logical and mathematical truths, which is a shame because those doubts are often reasonable, if not unavoidable.
B: I have the same response as before. Bayesianism is an ideal to strive towards. The platonic ideal of a scientist would be aware of all logical truths, but real world scientists obviously aren’t ideal.
N: Why is this ideal? Why should logically omniscient scientists be preferred over any other type of ideal? Why doesn't the ideal scientists already have access to all possible evidence? In that case, there would be no need to test theories because scientists would already know the outcome of every possible test.
B: This idealization would be unhelpful. It would not reveal much about how actual scientists behave or the methodologies they employ. Logical truths are a better idealization because logical truths aren't really relevant to scientific confirmation. Scientists don't deal with logical hypotheses; they deal with empirical hypotheses, and Bayesianism is great at dealing with those.
N: What about mathematicians? They do have to deal with mathematical/logical conjectures.
B: They can disregard Bayesianism and use conventional mathematical methods.
N: What about philosophers and computer scientists who need to combine logical conjectures with empirical evidence?
B: We might be able to tackle it with "logical uncertainty" but that’s still a developing field.
Alternatively we might give Bayesianism its own axioms that are similar, but not exactly the same axioms as probability theory. Maybe something like:
- Axiom 2: The credence that at least one of all the imagined outcomes of a process will occur is 1.
- Axiom 3: If two events A and B are imagined to be mutually exclusive, then the credence of either A or B occurring is the credence of A occurring plus the credence of B occurring.
P=NP is either necessarily true or necessarily false, but we can imagine untrue things. By allowing imagination to enter our axioms we can account for this discrepancy between our minds and the mathematical laws.
N: Interesting…
The problem of agnosticism
Bayliever: Does that answer all your questions?
Bagan: Nope! What are the Bayesian probabilities? The problem of logical omniscience suggests that we can't simply say they are degrees of belief, so what are they? Take a claim like "There are a billion planets outside the observable universe". How do you assign a probability to that? We can’t observe them, so we can’t rely on empiricism or mathematics, so... shouldn’t we be agnostic? How do we represent agnosticism in terms of probability assignments?
B: Prior probabilities can be anything you want. Just pick something at random between 0 and 1. It doesn’t really matter because our probabilities will converge over time given enough incoming data.
N: If I just pick a prior at random, that prior doesn’t represent my epistemic status. If I pick 0.7, I now have to pretend I’m 70% certain that there are a billion planets outside the observable universe, even though I feel totally agnostic. I’m not even sure we’ll ever find out whether there really are a billion planets outside the observable universe. Why can’t I just say that it’s somewhere between 0 and 1, but I don’t know where?
B: You need to be able to update. A rational thinker needs to have a definite value.
N: Why? There is no Dutch book argument against being agnostic. If someone offers me Dutch book bets based on the number of planets outside the observable universe, I can just decline.
B: What if you don’t have a choice? What if that person has a gun?
N: How would that person even resolve the bet? You’d have to know the amount of planets outside the observable universe.
B: It’s God, and God has a gun.
N: Okay, fine, but even in that absurd scenario I don’t have to have a definite value to take on bets. I can, for example, use a random procedure, like rolling a dice.
B: What if that procedure gives you a 0 or a 1? You would have a trapped prior, and you couldn’t update your beliefs no matter what evidence you observed.
N: I can’t update my beliefs if I follow Bayesianism. The axioms of probability theory allow me to assign a 0 or a 1 to a hypothesis. It’s Bayesianism that traps my priors.
B: You can’t assign a 0 or a 1 to an empirical hypothesis for that reason.
N: Isn’t that ad hoc? The probabilities were meant to represent an agent's degree of belief, and agents can certainly be certain about a belief. It seems the probabilities do not represent an agent's degree of belief after all. The Bayesian needs to add all sorts of extra rules, like that we can assign 0 and 1 to logical theorems but not empirical theories, which must actually be assigned a probability between 0 and 1. So... what are the probabilities exactly?
B: Hmmm… Let me get back to you on that one!
The problem of foreacting agents
Doubting Thomas: Say there is an agent whose behavior I want to anticipate. However, I know that this agent is:
- extremely good at predicting what I’m going to guess (maybe it’s an AI or a neuroscientist with a brain scanner) and…
- this agent wants me to make a successful prediction.
If I guess the agent has a 90% chance of pushing a button they will have already predicted it, and will afterwards push the button with 90% probability. Same with any other probability, they will predict it and set their probability for acting accordingly. It’s forecasting my guess and reacting before I predict, hence foreacting. After learning this information what should my posterior be? What probability should I assign to them pushing the button?
Thomas Bayes: Whatever you want to.
Doubting Thomas: But ‘whatever you want to’ is not a number between 0 and 1.
B: Just pick a number at random then.
N: If I just pick a prior at random, that doesn’t represent my epistemic state.
B: Ah, this is the problem of agnosticism again. I think I’ve found a solution. Instead of Bayesianism being about discrete numbers, we make it about ranges of numbers. So instead of saying the probability is around 0.7 we say it’s 0.6–0.8. That way we can say in this scenario and in the case of agnosticism that the range is 0–1.[3]
N: This would be an adequate solution to one of the problems, but can’t be a solution for both agnosticism and foreacting predictors.
B: Why not?
N: Because they don’t depict the same epistemic state. In fact, they represent an almost opposite state. With agnosticism I have basically no confidence in any prediction, whereas with the foreacting predictor I have ultimate confidence in all predictions. Also, what if the agent is foreacting non-uniformly? Let’s say it makes it’s probability of acting 40% and 60% if I predict it will be 40% and 60% respectively, but makes it’s probability not conform with my prediction when I predict anything else. So if I predict, say, 51% it will act with a probability of, say, 30%. Let’s also assume I know this about the predictor. Now the range is not 0–1, it’s not even 0.4–0.6 since it will act with a different probability when I predict 51%.
B: Hmmm…
N: And what if I have non-epistemic reasons to prefer one credence over another. Let’s say I’m trying to predict whether the foreacting agent will kill babies. I have a prior probability of 99% that it will. The agent foreacts, and I observe that it does indeed kill a baby. Now I learn it’s a foreacting agent. With Bayesianism I keep my credence at 99%, but surely I ought to switch to 0%. 0% is the ‘moral credence’.
B: This is a farfetched scenario.
N: Similar things can happen in e.g. a prediction market. If the market participants think an agent has a 100% probability of killing a baby they will bet on 100%. But if they then learn that the agent will 100% kill the baby if they bet on 1%-100%, but will not kill the baby if the market is 0% they have a problem. Each individual participant might want to switch to 0%, but if they act first the other participants are financially incentivized to not switch. You have a coordination problem. The market causes the bad outcome. You don’t even need foreacting for this, a reacting market is enough. Also, there might be disagreement on what the ‘moral credence’ even is. In such a scenario the first buyers can set the equilibrium and thus cause an outcome that the majority might not want.[4]
B: This talk about ‘moral credences’ is besides the point. Epistemology is not about morality. Bayesianism picks an accurate credence and that’s all it needs to do.
N: But if two credences are equally good epistemically, but one is better morally, shouldn’t you have a system that picks the more moral one?
B: Alright, what if we make Bayesianism not about discrete numbers, nor about ranges, but instead about distributions? On the x-axis we put all the credences you could pick (so any number between 0 and 1) and on the y-axis what you think the probability will be based on which number you pick.
So when you encounter a phenomenon that you think has a 60% chance of occurring (no matter what you predict/which credence you pick) the graph looks like this:
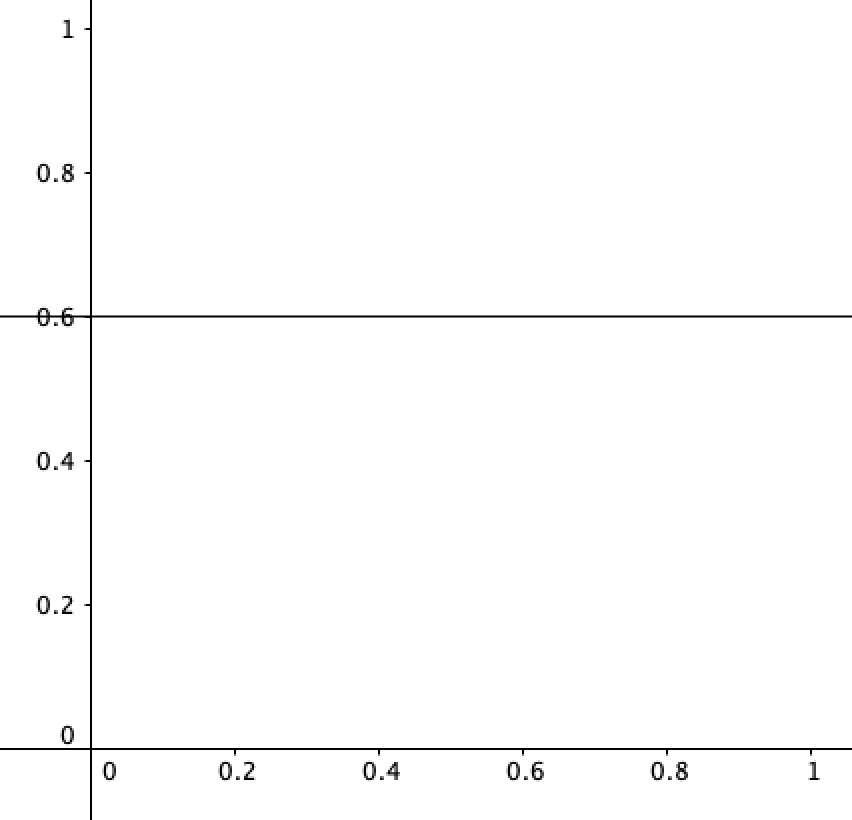
And when you encounter a uniformly foreacting agent who (you believe) makes the odds of something occurring conform to what you predict (either in your head or out loud), you have a uniform distribution:
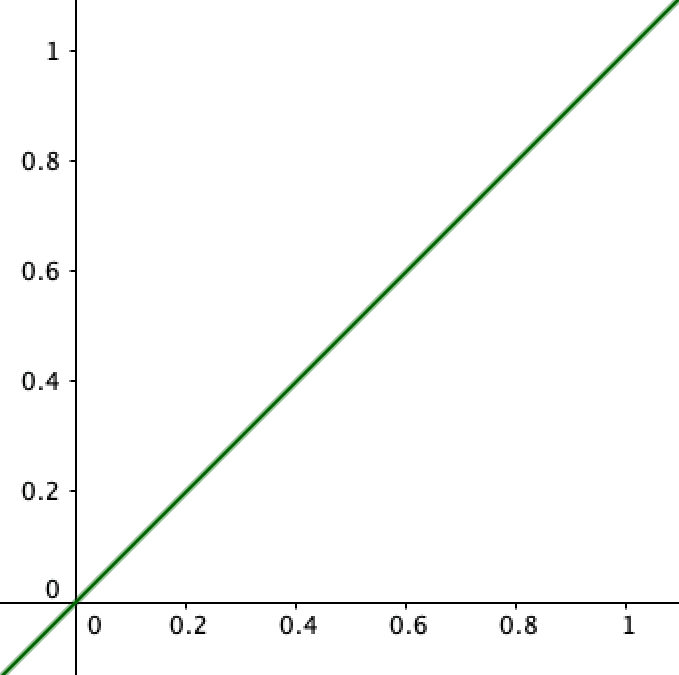
With this you can just pick any number and be correct. However if you encounter the non-uniformly foreacting agent of your example the graph could look something like this: (green line included for the sake of comparison)
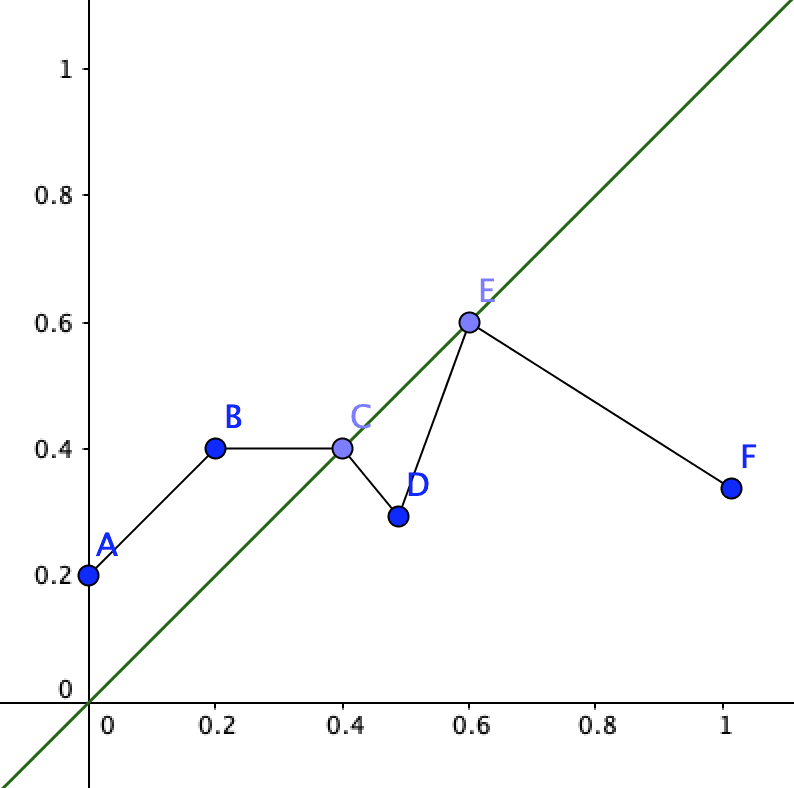
Picking 0.2 (B) will result in the predictor giving you a terrible track record (0.4). But picking 0.4 or 0.6 (C or E) will give you an incredible track record. Let’s call C and E ‘overlap points’. If this distribution is about whether the agent will kill a baby, C is the ‘moral credence’.
N: Wouldn’t A be the moral credence, since that has the lowest chance of killing a baby?
B: Humans can’t will themselves to believe A since they know that predicting a 0% chance will actually result in a 20% chance.
N: What about an agent that is especially good at self deception?
B: Right, so if you have e.g. an AI that can tamper with it’s own memories, it might have a moral duty to delete the memory that 0% will result in 20% and instead forge a memory that 0% will lead to 0%, just so the baby only has a 20% chance of dying.
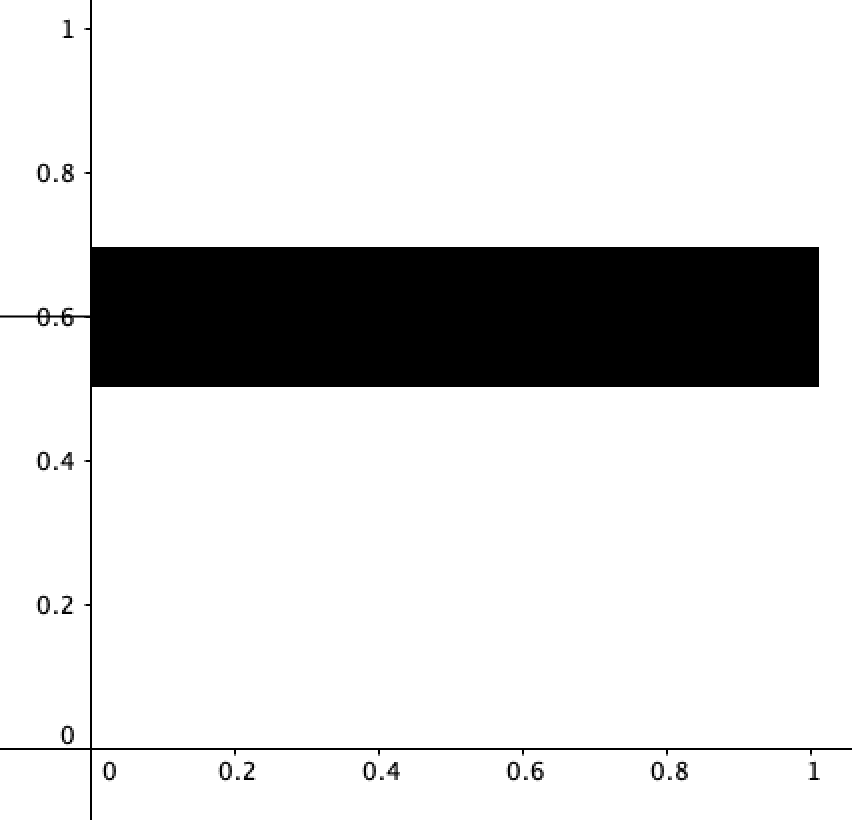
N: What if you have a range? What if you don’t know what the probability of something is but you know it’s somewhere between 0.5 and 0.7?
B: Then it wouldn’t be thin line at 0.6, but a ‘thick’ line, a field:
N: What about total agnosticism?
B: Agnosticism would be a black box instead of a line:

The point could be anywhere between here, but you don’t know where.
N: What if you’re partially agnostic with regards to a foreacting agent?
B: This method allows for that too. If you know what the probabilities are for the foreacting agent from A to E, but are completely clueless about E to F it looks like this:
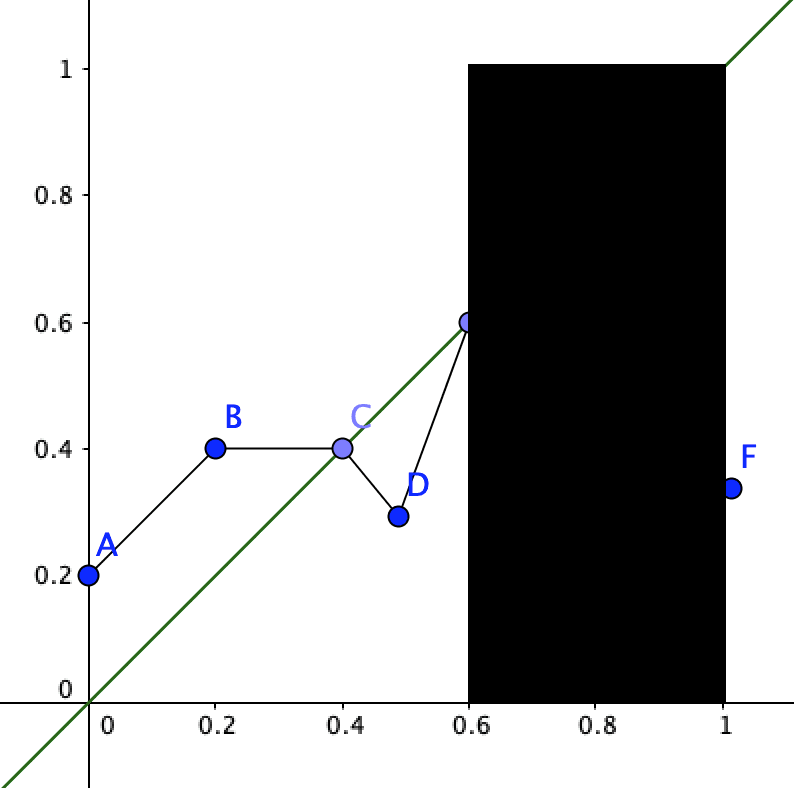
N: What if I don’t know the probabilities of the agent between E and F, but I do know it's somewhere between 0.2 and 0.6?
B: It would look something like this:

N: What if it doesn’t foreact to your credences, but the graph as a whole?
B: Then you add an axis, if it reacts to that you add another axis etc.
N: This is still rather abstract, can you be more mathematical?
B: Sure!
Applying Bayesian modeling and updating to foreacting agents
To apply the Bayesian method, the main thing we need is a world model, which we can then use to calculate posterior probability distributions for things we are interested in. The world model is a Bayesian network that has…
- one node for each relevant variable X
- one directed arrow Y→X for each direct dependency among such variables, leading from a parent node Y to a child node X
- and for each node X a formula that calculates the probability distribution for that variable from the values of all its parents: P(X | parents(X))
For nodes X without parents, the latter formula specifies an unconditional probability distribution: P(X | parents(X)) = P(X | empty set) = P(X).
In our case, I believe the proper model should be this:
- Variables:
- B: whether the agent will press the button. This is a boolean variable with possible values True and False.
- p: the credence you assign to the event B=True. This is a real-valued variable with possible values 0…1
- q: the probability that the agent uses to decide whether to press the button or not. This is also a real-valued variable with possible values 0…1
- Dependencies:
- B depends only on q: parents(B) = {q}
- q depends only on p: parents(q) = {p}
- Formulas for all variables’ (conditional) probability distributions:
- P(B=True | q) = q, P(B=False | q) = 1 – q
- P(q | p) is given by two functions flow, fhigh as follows:
- If flow(p) = fhigh(p) = f(p), then q = f(p), in other words: P(q | p) = 1 iff q = flow(p) and 0 otherwise
- If flow(p) < fhigh(p), then P(q | p) has uniform density 1 / (fhigh(p) – flow(p) for flow(p) < q < fhigh(p) and 0 otherwise.
- For the uniformly foreacting agent agent we have flow(p) = fhigh(p) = f(p) = p
- Note that we assume to know the response function upfront, so the functions flow, fhigh are not variables of the model but fixed parameters in this analysis. We might later study models in which you are told the nature of the agent only at some time point and where we therefore also model flow, fhigh as a variable, but that gets harder to denote then.
- P(p) = whatever you initially believe about what credence you assign to the event B=True
At this point, we might be surprising necessity of the Bayesian method and get a little wary: because our model of the situation contains statements about how our credence in some variable influences that variable, we needed to include both that variable (B) and our credence (p) as nodes into the Bayesian network. Since we have to specify probability distributions for each parentless node in the network, we need to specify them about p, i.e., a probability distribution on all possible values of p, i.e., a credence about our credence in B being 0.3, a credence about our credence in Bbeing 0.7, etc. This is the P(p) in the last line above. In other words, we need to specify 2nd-order credences! Let us for now assume that P(p) is given by a probability density g(p) for some given function g.
The whole model thus have two parameters:
- two functions flow, fhigh encoding what you know about how the agent will choose q depending on p,
- and a function g encoding your beliefs about your credence p.
The Bayesian network can directly be used to make predictions. Making a prediction here is nothing else than calculating the probability of an event.
- In our case, we can calculate
P(B=True) = integral of P(B=True | q) dP(q) over all possible values of q
= integral of P(B=True | q) dP(q | p) dP(p) over all possible values of q and p
= integral of f(p) g(p) dp over p=0…1 (if flow=fhigh=f, otherwise a little more complicated)
- For example:
- If we consider the uniformly foreacting agent with f(p) = p and believe that we will assign credence p = 0.3 for sure, then P(B=True) = 0.3 and we are happy.
- If we consider the uniformly foreacting agent with f(p) = p and believe that we will assign either credence p=0.3 or p=0.8, each with probability 50%, then P(B=True) = 0.55 and we are unhappy.
- If we consider any f for which there is at least one possible value p* of p such that f(p*)=p*, and believe that we will assign credence p = p*, then P(B=True) = f(p*) = p* and we are happy.
- If we consider an f for which there is no possible value p with f(p)=p, and believe that we will assign some particular credence p* for sure, then we get P(B=True) != p* and will be unhappy.
- But: If we consider an f for which there is no possible value p with f(p)=p, and believe that we might assign any possible credence value p between 0 and 1 with some positive probability, then we indeed get some result P(B=True) between 0 and 1, and since we have attached positive probability to that value, we should be happy since the result does not contradict what we believed we would predict!
Let’s assume we interpret the node p as a control variable of a rational us with some utility function u(B), let’s say u(B=True) = 1 and u(B=False) = 0. Then we can use the Bayesian model to calculate the expected utility given all possible values of p: E(u(B) | p) = q = (flow(p) + fhigh(p)) / 2. So a rational agent would choose that p which maximizes (flow(p) + fhigh(p)) / 2. If this is all we want from the model, we don’t need g! So we only need an incomplete Bayesian network which does not specify the probability distributions of control variables, since we will choose them.
Things get more interesting if u depends on B but also on whether p = q, e.g. u(B,p,q) = 1B=True – |p – q| . In that case, E(u | p) = f(p) – |p – f(p)|. If f(p) > p, this equals f(p) – |f(p) – p| = f(p) – (f(p) – p) = p. If f(p) < p, this equals 2f(p) – p.
Let’s assume the rational us cannot choose a p for which f(p) != p.
Excursion: If you are uncertain about whether your utility function equals u1 or u2 and give credence c1 to u1 and c2 to u2, then you can simply use the function u = c1*u1 + c2*u2.
Bayesian updating is the following process:
- We keep track of what you know (rather than just believe!) about which combinations of variable values are still possible given the data you have. We model this knowledge via a set D: the set of all possible variable value combinations that are still possible according to your data (Formally, D is a subset of the probability space Omega). If at first you have no data at all, D simply contains all possible variable combinations, i.e., D=Omega.
- In our case, D and Omega equal the set of all possible value triples (B,p,q), i.e., they are the Cartesian product of the sets {True,False}, the interval [0,1] and another copy of the interval [0,1]:
- D = Omega = {True,False} x [0,1] x [0,1]
- In our case, D and Omega equal the set of all possible value triples (B,p,q), i.e., they are the Cartesian product of the sets {True,False}, the interval [0,1] and another copy of the interval [0,1]:
- Whenever we get more data:
- We reflect this by throwing out those elements of D that are ruled out by the incoming data and are thus no longer considered possible. In other words, we replace D by some subset D’ of D.
- Then we calculate the conditional probability distribution of those events E we are interested in, given D, using Bayes’ formula:
- P(E | D) = P(E and D) / P(D)
At this point, we might be tempted to treat the value we derived for P(B=True) on the basis of some choice of f and g as data about p. Let’s consider the consequences of that. Let’s assume we start with some fixed f, g and with no knowledge about the actual values of the three variables, i.e., with D0 = Omega = {True,False} x [0,1] x [0,1]. We then calculate P(B=True) and get some value p1 between 0 and 1. We treat this as evidence for the fact that p = p1 update our cumulative data to D1 = {True,False} x {p1} x [0,1], and update our probabilities so that now P(B=True) = f(p1). If the latter value, let’s call it p2, equals p1, we are happy. Otherwise, we wonder. We have then several alternative avenues to pursue:
- We can treat the result P(B=True) = p2 as another incoming data about p, which needs to be combined with our earlier data. But our earlier data and this new data contradict each other. Not both can be true at the same time, so the statement S1: p = p1 , that was suggested by our earlier data is false, or the statement S2: p = p2 that was suggested by our earlier data is false. If we consider that S1 is false, we must consider why it is false since that might enable us to draw valuable conclusions. S1 was derived purely from our world model, parameterized by the functions f and g, so either at least one of those functions must have been incorrect or the whole model was incorrect.
- The shakiest part of the model is g, so we should probably conclude that our choice of g was incorrect. We should then try to find a specification of g that does not lead to such a contradiction. We can only succeed in doing so if there is a value p* for which f(p*) = p*. If such a value exists, we can put g(p*) = infinity (remember, g specifies probability densities rather than probabilities) and g(p) = 0 for all p != p*, i.e., assume from the beginning that we will predict p* for sure. But if such a value p* does not exist, we cannotchoose g so that the contradiction is avoided.
- In that case, something else about the model must have been incorrect, and the next best candidate for what is wrong is the function f. Since no p with f(p)=p exists, f must be discontinuous. Does it make sense to assume a discontinuous f? Probably not. So we replace f by some continuous function. And et voila: now there is some value p* with f(p*)=p*, and we can now choose a suitable gand avoid the contradiction.
- If we desperately want to stick to a discontinuous f, then something else about the model must be wrong. I think it is the idea of the agent being able to know p with certainty, rather than just being able to measure p with some random measurement noise epsilon. I suggest adding two more variables, the noise epsilon and the measurement m, and modify the formulae as follows:
- epsilon ~ N(0,1), i.e., Gaussian noise
- m = h(p, epsilon) for some continuous function h that represents the influence of the random noise epsilon on the agent’s measurement m of p.
- For example: h(p, epsilon) = expit(logit(p) + sigma epsilon) for some magnitude parameter sigma > 0.
- q = f(m) rather than q = f(p)
With this modified model, we will get
P(B=True) = integral of P(B=True | q) dP(q) over all possible values of q
= integral of P(B=True | q) dP(q | m) dP(m | p, epsilon) dP(p) dP(epsilon) over all possible values of q, p and epsilon
= integral of Eepsilon~N(0,1)f(h(p, epsilon)) g(p) dp over p=0…1, where E is the expectation operator w.r.t. epsilon
If our choice of g assigns 100% probability to a certain value p1 of p, the calculation results in
p2 := P(B=True) = Eepsilon~N(0,1)f(h(p1, epsilon)),
which is a continuous function of p1 even if f is discontinuous, due to the “smearing out” performed by h! So there is some choice of p1 for which p2 = p1 without contradiction. This means that whatever continuous noise function h and possibly discontinuous reaction function f we assume, we can specify a function g encoding our certain belief that we will predict p1, and the Bayesian network will spit out a prediction p2 that exactly matches our assumption p1.[5]
Acknowledgment
A huge thanks to Jobst Heitzig for checking my writing and for writing the “Applying Bayesian modeling and updating to foreacting agents” section of the post. He says it's incomplete and there's more to be written, but I'm thankful for what's already there. And special thanks to the countless people who provide the free secondary literature on philosophy which makes me understand these problems better. You all deserve my tuition money.
- ^
For an article on this see Why I am not a Bayesian by Clark Glymour
- ^
You can use this to make an absent-minded driver problem for social epistemology
- ^
- ^
Let’s hope that the first people in a prediction market don’t have different interests than the population at large. What are the demographics of people who use prediction markets again?
- ^
Alternatively, we could conclude that the output of the Bayesian network, P(B=True), should not be treated as data on p. But then what?

Interesting work! One of my main annoyances with pop-Bayesianism as practiced casually by EA is the focus on giving single number estimates with no uncertainty ranges.
In contrast, a primer on Bayesian statistics will switch to distributions pretty much immediately. If you Wikipedia "prior", you immediately get "prior probability distribution". I blame the sequences for this, which seemingly decided to just stay in Bayes 101 territory and barely mention Bayes 102.
I'm curious about your methodology: Is it based on existing Bayesian statistical methods, or a competing theory? Do you think it could be approximated in a way that would help a casual user make approximate predictions? How would you apply it to a real world problem, like the "P(doom)" issue that everyone is always going on about?
Thank you!
Yes, I agree distributions are better than single numbers. I think part of the problem for podcasts/conversations is that it's easier to quickly say a number than a probability distribution, though that excuse works slightly less well for the written medium.
I didn't base it off an existing method. While @Jobst tells me I have good "math instincts" that has yet to translate itself into actually being good at math, so this mostly comes from me reading the philosophical literature and trying to come up with solutions to some of the proposed problems. Maybe something similar already exists in math, though Jobst and some people he talked to didn't know of it and they're professional mathematicians.
As for casual users, I would urge them to take 'agnosticism' (or at least large ranges) seriously. Sometimes we really do not know something and the EA culture of urging people to put a number on something can give us a false sense of confidence that we understand it. Especially in scenarios of interactions between agents where mind games can cause estimations to behave irregularly. I mentioned how this can go wrong with a prediction market, but a version of that can happen with any group project. Regular human beings do on occasion foreact e.g. If we know we like each-other, and I think you'll expect me to do something on a special day, the chance that I will do it is higher than if I didn't think so.
All of this doesn't even mention a problem with Bayesianism I wasn't able to solve, the absent-minded driver problem. Once we add fallible memories to foreaction the math goes well beyond me.
I don't know what "P(doom)" means. Even beyond the whole problem of modeling billions of interacting irrational agents some of whom will change their behavior based on what I predict, I just don't think the question is clear. Like, if I do something that decreases the chance of a sharp global welfare regression, increases the chance of an s-risk, and has no effect on x-risk, what happens to P(doom)? Are we all talking about the same thing? Shouldn't this at the very least be two variables, one for probability and one for how "doom-y" it is? Wouldn't that variable be different depending on your normative framework? What about inequality-aversion, if there is one super duper über happy utility monster and all other life is wiped out, is that a 'doom' scenario? What about time discounting, does the heat death of the universe mean that P(doom) is 1? I don't know, P(doom) confuses me.