Update (14 Aug 2025): The code generating results in Table 4 (optimal pause decisions) contained an error leading to local rather than global optimization. I have left Table 4 in it's original form, but new code can be found here which reveals optimal non-zero pauses for and .
In this post I first summarize a recent paper by Chad Jones focused on the decision to deploy AI that has the potential to increase both economic growth and existential risk (section 1). Jones offers some simple insights which I think could be interesting for effective altruists and may be influential for how policy-makers think about trade-offs related to existential risk. I then consider some extensions which make the problem more realistic, but more complicated (section 2). These extensions include the possibility of pausing deployment of advanced AI to work on AI safety, as well allowing for the possibility of economic growth outside of deployment of AI (I show this weakens the case for accepting high levels of risk from AI).
At times, I have slightly adjusted notation used by Jones where I thought it would be helpful to further simplify some of the key points.[1]
I. Summary
AI may boost economic growth to a degree never seen before. Davidson (2021), for example, suggests a tentative 30% probability in greater than 30% growth lasting at least ten years before 2100. As many in the effective altruism community are acutely aware, advanced AI may also pose risks, perhaps even a risk of human extinction.
The decision problem that Jones introduces is: given the potential for unusually high economic growth from AI, how much existential risk should we be willing to tolerate to deploy this AI? In his simple framework, Jones demonstrates that this tolerance is mainly determined by three factors: the growth benefits that AI may bring, the threat that AI poses, and the parameter that underlies how utility is influenced by consumption levels.
Here, I will talk in the language of a ‘social planner’ who applies some discount to future welfare; a discount rate in the range of 2%-4% seems to be roughly in line with that rate applied in the US and UK,[2] though longtermists may generally choose to calibrate with a lower discount rate (eg. <1%). In the rest of this post when I say 'it is optimal to...' or something to this effect, this is just shorthand for: 'for social planner who gets to make decisions about AI deployment with a discount rate X, it is optimal to...'.
The Basic Economic Framework
Utility functions (Bounded and unbounded)
A utility function is an expression which assigns some value to particular states of the world for, let’s say, individual people. Here, Jones (and often macroeconomics more generally) assumes that utility for an individual is just a function of their consumption. The so called ‘constant relative risk aversion’ utility function assumes utility is given by
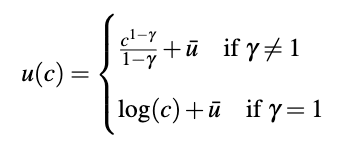
Where is consumption, and and
will be helpful to calibrate this utility function for real-world applications, where
adjusts the curvature and
scales utility up or down.[3] There is a key difference between these two functions (more specifically, when
vs
): for
utility is bounded above, while for
utility is not. A utility function is bounded above if, as consumption increases to infinity, utility rises toward an upper bound that isn’t infinite. A utility function is unbounded above if, as consumption increases to infinity, utility does too.
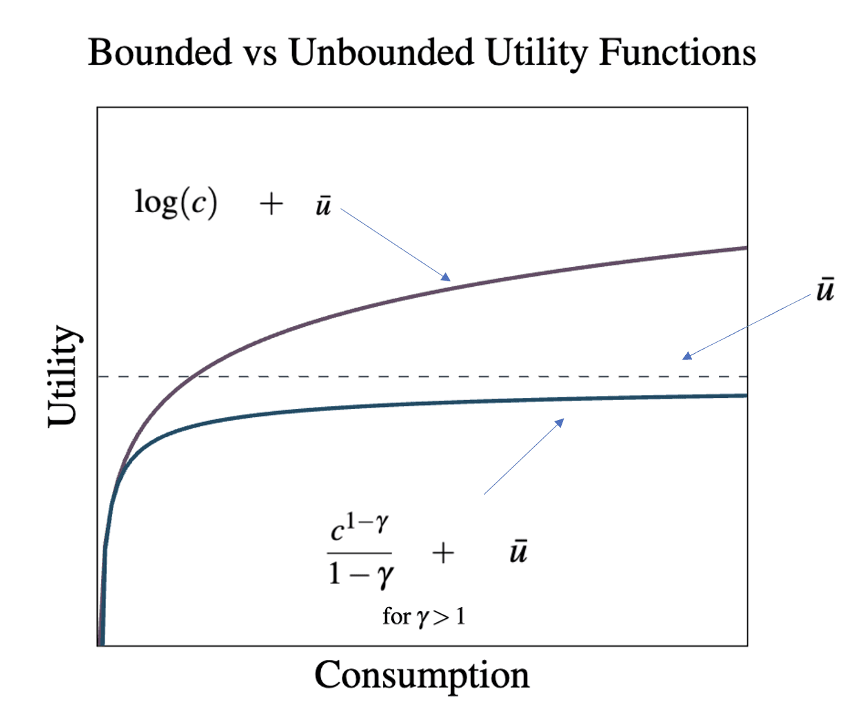
The distinction between bounded and unbounded utility functions becomes particularly important when considering the growth benefits of AI, since prolonged periods of high growth can cause us to move along x-axis (of the above plot) quite far. In the most extreme case, Jones considers what happens to our willingness to deploy AI when that AI will be guaranteed to deliver an economic singularity (infinite growth in finite time). In this case we can see that if utility is unbounded then infinite consumption results in infinite gains to utility. In this case, any amount of risk less than guaranteed extinction could justify the infinite welfare gains from a singularity.[4]
In short, we can see that when thinking about extreme growth scenarios, which utility function you apply can be extremely important.
The Value of a Year of Life (in utility terms)
Before applying our utility function to the growth vs risk trade-off, first we need to calibrate it. A useful term here is the value of a statistical life year. Surveys indicate that, in the US, an extra year of life is worth about 6 times the average per-capita consumption. Call this term . Now, we can also recover this value directly out of our utility function, where (and is the derivative of the utility function).[5] If we then set
(since we are interested in the value of life as a multiple of today’s consumption) and
, along with a given value of
, we can solve for
(as a function of 𝛾).
In the subsequent sections three different calibrations of are considered (
) which yield the following utility in terms of multiples of current annual consumption:
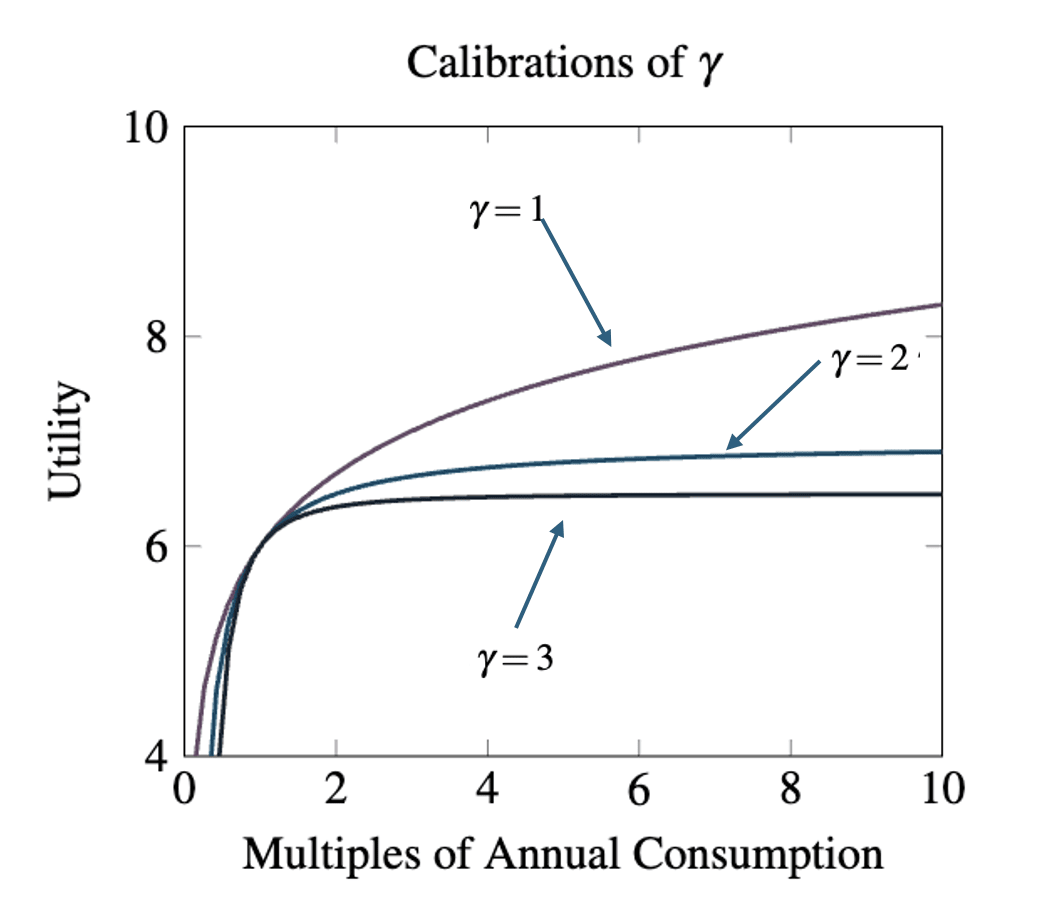
Here the utility function is bounded below 7 (i.e.,
) while the
utility function is bounded below 6.5 (i.e.,
).[6]
How should we trade off growth and existential risk?
In order to understand the trade-off between risk and growth, Jones considers a simplified example of deployment of AI: suppose we can ‘turn on’ AI for some length of time, increasing existential risk, before choosing to ‘shut it down’. While the AI is ‘on’ we get to enjoy some unusually high growth rate and then once the AI is shut down there is no growth. (At this point, Jones assumes there is no population growth and constant discounting).
To reflect this trade-off we need two parameters: the annual risk of extinction while AI is turned on, and
the annual growth rate while AI is turned on.
To make this problem as simple as possible, Jones assumes that before we have access to this model which grants us unusual growth we just decide how long we will leave it on for, this length of time is just called . The total risk from leaving the model on for
periods is just going to be (where is the annual risk of extinction while AI is turned on)
. Jones just assumes once we make this decision we face all of this risk immediately; in effect we roll a die that gives us a
chance of all dying immediately. A similar simplification is repeated for consumption: we enjoy a constant level of consumption,
, immediately (rather than having this grow over time), assuming we survive the initial roll of the dice. The longer we choose to leave the AI on for, the greater our consumption will be.
Under these conditions we have this simplified, expected welfare function:
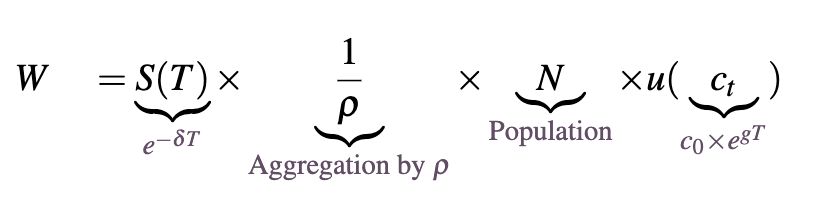
Here is the constant discount rate, though one could also interpret this as annual existential risk that comes from sources other than AI. [7] Multiplying welfare by
amounts to ‘scaling up’ the initial level of welfare according to how quickly the flow of welfare diminishes over time through discounting (eg. with
this scales up welfare by a factor of 20 to account for the value of the future, while
scales up welfare by a factor of 100). We can see here that increasing
will increase our consumption due to the positive exponent in
and decrease our survival probability due to the negative exponent in .
To find the T that maximises welfare, we set the derivative of with respect to
equal to zero. This leads to the result that we should leave the AI on until the value of life at that consumption level is equal to the ratio of the growth benefits to the existential risk:
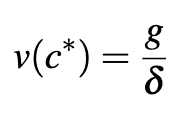
As an example, if AI were to grant us 30% annual growth but pose a 1% annual risk, we should run AI until a year of life is worth 30 times our annual consumption. When is higher, this means it is optimal to allow value of life to increase higher before turning off AI, while increasing
has the opposite effect. Since all benefits from AI are realised immediately in this economic environment, discounting has no impact on optimal shut down decisions for AI.
We could also adjust this expected welfare function to see what would happen if deployment of AI could deliver a boost in the population along with a boost in consumption (for example, perhaps it could deliver medical technology advances, allow us to colonize other planets, or deliver digital minds). If we suppose that while the AI is turned on we had population growth at rate (an no population growth otherwise) then we can just replace
in the above expected welfare function with
where is the initial population level. This would give us the decision rule a population growth-adjusted decision rule:
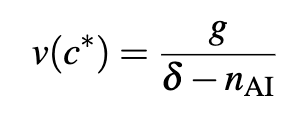
Jones makes the point that in contrast to consumption, increasing the number of people is ‘in the same units’ as existential risk since both are just talking about the number of people who exist. In this decision rule, because risk and population growth benefits are in the ‘same units’, any population growth benefits directly offset the losses associated with risks from AI. For example, if and
then this reduces the ‘effective’ existential risk to . Further, if , this would imply that for any given length of time running the AI, we could always do at least as well by running it for an additional year.[8]
Quantitative example
Jones considers a handful of calibrations to give some sense of scale for the results of this simple model (where the growth rate under AI is assumed to be 10%):
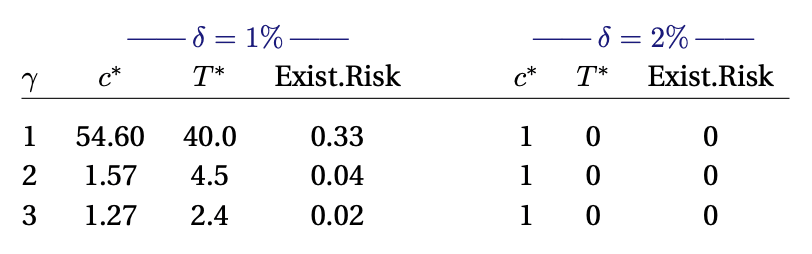
First, looking at the column, we can see that when we increase the curvature of the utility function (through increasing
) this decreases our willingness to allow the model to run, increasing the probability of survival. However, under higher calibrations of risk, this risk is high enough such that we should never risk turning on the AI in the first place, that is
where is our current level of consumption. Looking down the rows we can see that the shape of the utility function can be critical for determining how long we should run the AI for. In more curved utility functions
() the welfare gains from AI-induced growth diminish relatively quickly, whereas under log-utility these gains persist for much longer leading to the decision to allow AI to run for a much longer time.
While this example introduced here is a very simplified one, I think it makes clear an important consideration when it comes to the promise and threat of AI: the shape of our utility function is important.
What if AI could lead to a singularity?
To evaluate the impact of an AI-induced economic singularity on the willingness to deploy advanced AI models, Jones develops a richer model to illustrate ‘cut-off’ risk – the maximum level of existential risk from AI such that society would be willing to deploy that model. The model considered here is ‘richer’ than that introduced initially because it considers consumption and population growth over time rather than these levels being realized immediately and allows the social planner to discount at some rate different to the rate individuals tend to discount their own future utility (though any existential risk is still assumed to be realized immediately). In this environment Jones gives us two options: permanently deploy AI or never deploy it at all.
This gives the welfare function:
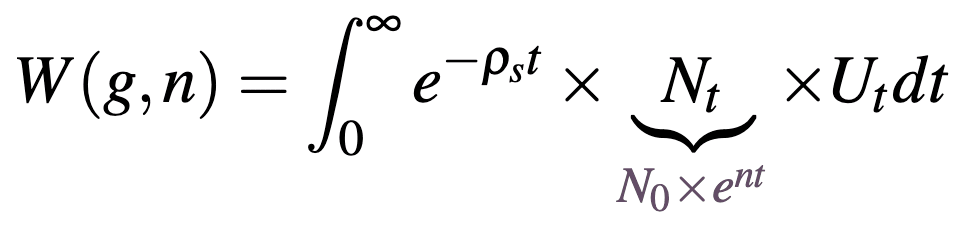
where
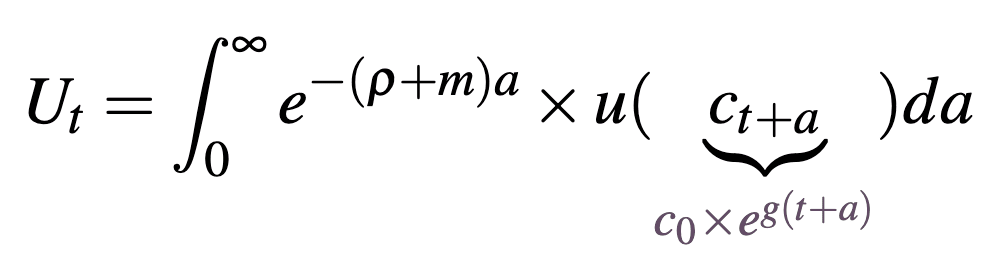
this welfare function aggregates the utility of individuals born at time that experience a lifetime utility for , discounted at the social discount rate . Lifetime utility aggregates an individual's utility at each age in their life, discounted by the sum of their individual discount rate and their risk of dying at each age . Here is an individual's life expectancy (). By distinguishing between an individual and a social discount rate we can set according to the value that we think government should discount the welfare of future generations (longtermists will generally set this value close to zero) while still respecting the fact that individuals might discount their own future utility at a different rate (this may be inferred through an individual's market behaviour). [9]
Now, as the social planner has to decide between deploying and not, the planner will chose to deploy AI so long as
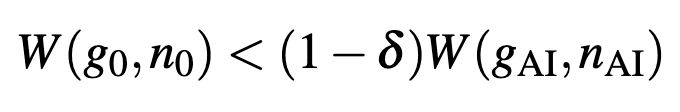
where variables subscripted with 0 are the economic and population growth without AI.
To give help generate quantitative results, Jones defines as the ‘cut-off’ risk given values of population and economic growth:
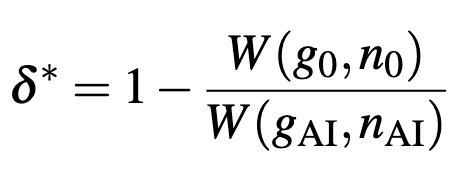
If this cut-off is high (close to 1) that means that we will be willing to tolerate a lot of risk to run the AI, and while this value is low (close to zero) the model would have to be very safe to justify deployment.
Quantitative results
Calibrating welfare functions (including setting , , and along with ) gives us the following results:
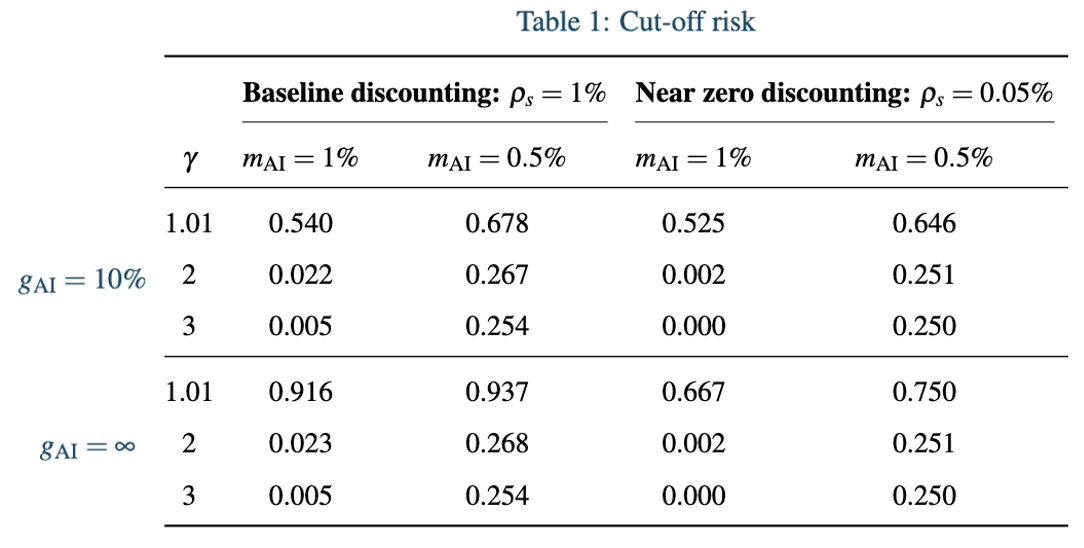
As we can see from the table above with close to 1 and AI delivering a singularity, the social planner will be willing to tolerate almost certain existential catastrophe for the shot at the massive welfare gains from a singularity.
Looking back to the expression for , we can see large changes in the cut-off risk after changing the discount rate must mean the discount rate scales differently from when . Specifically, lowering the discount rate increases much more than when AI offers an immediate singularity. This is because constant 2% economic growth means that future generations are wealthier than present generations and lowering the discount rate assigns more value to the welfare contributions from those future generations. For a singularity, all generations enjoy infinite consumption once AI is deployed so lowering the discount rate has a more mild impact on .
With changes in the population growth rate the story is a bit different. We can see that this benefit pretty consistently increases our cut-off risk. This is a consequence of total utilitarianism, under which, welfare doesn’t diminish with population size (unlike the returns for increased consumption). I it to a footnote to discuss why cut-off risk seems to approach 0.25 when .[10]
Some thoughts
I think this paper does a good job of identifying how trade-offs related to the promise and threat from AI can be considered in a simple economic framework. Though this simplicity makes it difficult to apply any of the quantitative insights to actual decisions about how we approach the use of AI (at least, without some testing of the quantitative implications of additional considerations). In this vein, we may want to consider relevant points like:
- The rate of economic growth outside of times when we are running this AI model.
- In the optimal deployment time example, Jones assumes there is no growth outside of times when we are running AI. In the problem he lays out we have to choose between any growth at all and AI risk. In reality we should expect to enjoy at least some economic growth without AI.
- That we may take actions to increase AI safety, which can influence the optimal deployment decision.
In the following extension to this paper I make a first pass at considering both of these possibilities and provide some quantitative results. The extension suggested in point 1 above seems to have a pretty modest effect on the quantitative results, while the extension suggested in point 2 can have quite a large impact on these results. I still don’t expect the results for this extension to capture all of the relevant considerations around the deployment of an advanced AI system (and so I caution against taking the following results too literally). But I do think that the impact of these additional considerations may be helpful for those thinking about the implications of the Jones results.[11]
II. Extensions for EAs
When to shut down AI when there is non-AI economic growth?
Departing from the approach of Jones outlined above, in this first extension I now allow risk to be realised over time, and for there to be 2% annual growth outside of the years where AI is deployed. This gives us the welfare function (assuming constant population and that individuals and the social planner discount at the same rate):
We can see here that during deployment there is ongoing existential risk, and the welfare after deployment is multiplied by to capture the probability that we survive the deployment period.
Below I compare the optimal deployment window under no AI growth (as provided above), which I here call to this window when there is growth outside deployment of AI, which I call .[12]

Looking at the results when allowing for economic growth outside of deployment of AI, unsurprisingly, we can see that this growth will reduce the optimal deployment window for AI. This window changes most significantly in the case of and : under
this window declines from 37 to 15 years, and for
and
this additional growth means that a planner will no longer be willing to deploy AI at all. More generally, one can show that, while
and
, AI should never be deployed for any . For the rest of the calibrations of
and
, the impact of non-AI growth is more modest (and this has no impact at all when
and
since we were never willing to deploy AI in the first place). The reason that the effects of growth outside AI deployment are modest when
is just because when growth occurs this fast, the benefits of constant 2% economic growth once we shut off the AI are lower. This is just the result of diminishing marginal utility from consumption.
Welfare effects of a six month pause on AI
Pausing capabilities research may allow us to advance AI safety research, lowering the annual existential risk of AI once it is deployed. The Jones paper gives us a framework for considering the welfare consequences of such a pause. In this setting, the welfare effects of a six month pause are not immediately obvious. On one hand, taking a six month pause may allow us to reduce the risk from AI once it is deployed. On the other, taking a six month pause may cause us to miss out on the opportunity to boost economic growth in the short term.
In particular, I consider the welfare impact of a 6 month pause on deployment of AI. This pause will reduce the annual existential risk of deployed AI from to , where I assume
is either 5 or 10% smaller than the calibration of ; e.g., if prior to pausing, annual existential from deploying AI was 1%, pausing would reduce this to either 0.9% or 0.95%. As in the extension considered above, I will allow there to be 2% annual economic growth during the pause period and after the AI is shut-off and that existential risk is realized over time. Here we have the following expected welfare function:
Where is the pause period, which is set to 0.5 to reflect the six month pause. Here we can call
: the length of time that AI runs after the pause period. Following the same procedure as above, the following table details how the optimal time spent running the AI changes after a pause period (when we assume there is 30% economic growth under deployed AI and 1% annual existential risk without a pause) and how the pause period changes the expected future value of the future in welfare terms:
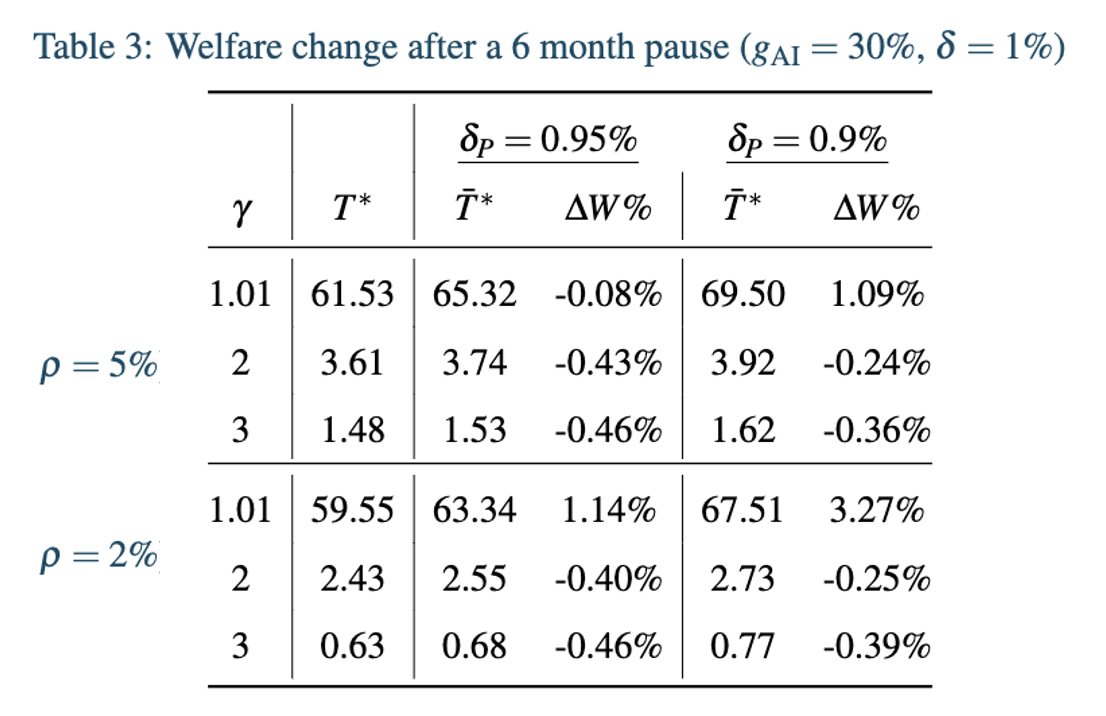
Where is the percentage change in welfare after making the optimal deployment decision after a six month pause, relative to the no pause optimal decision.
As we can see, after a pause period we are always willing to run the AI for longer, since the risk will always be lower. However, out of the cases considered the only time that taking a pause increases welfare is when we have relatively low curvature of our utility function and either we have a low discount rate or this pause period comes with a 10% reduction in annual existential risk from AI deployment. In all the rest of the cases this pause reduces our welfare. This reduction comes from a pause delaying the time where we can access the growth benefits; delaying these benefits incurs an implicit cost due to discounting.
If we only consider the growth and existential risk trade-off, as I do in this model, then a six month pause can have very significant positive effects. In the calibrations considered above, such a pause can increase the (discounted) value of the future by up to 3.27%. Of course, losses in the range of 0.4% of future welfare would be very bad, and hence if we were to take this model with any seriousness (which I would be very cautious of) then this points to the importance of careful thinking about the correct calibrations, particularly when it comes to the shape of the utility function.
Optimal pause on AI
For this final quantitative exercise I consider the optimal length of pause on AI. This amounts to not holding fixed in the welfare function described above so that a social planner has to choose and to optimize welfare. Above I assumed that the annual existential risk after a six month pause took on either 0.95% or 0.9%
. Here I will assume that when AI is paused,
declines exponentially with the length of the pause period:
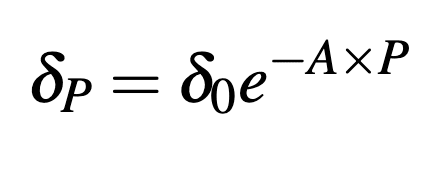
Where is some non-negative scaling factor: if then the annual existential risk from AI during deployment declines from its original value at 10% per year during the pause period. In this way, we can pause AI for as long as we want to reduce existential risk from deployment. This gives us the following optimal choices of pause (and deployment) time:
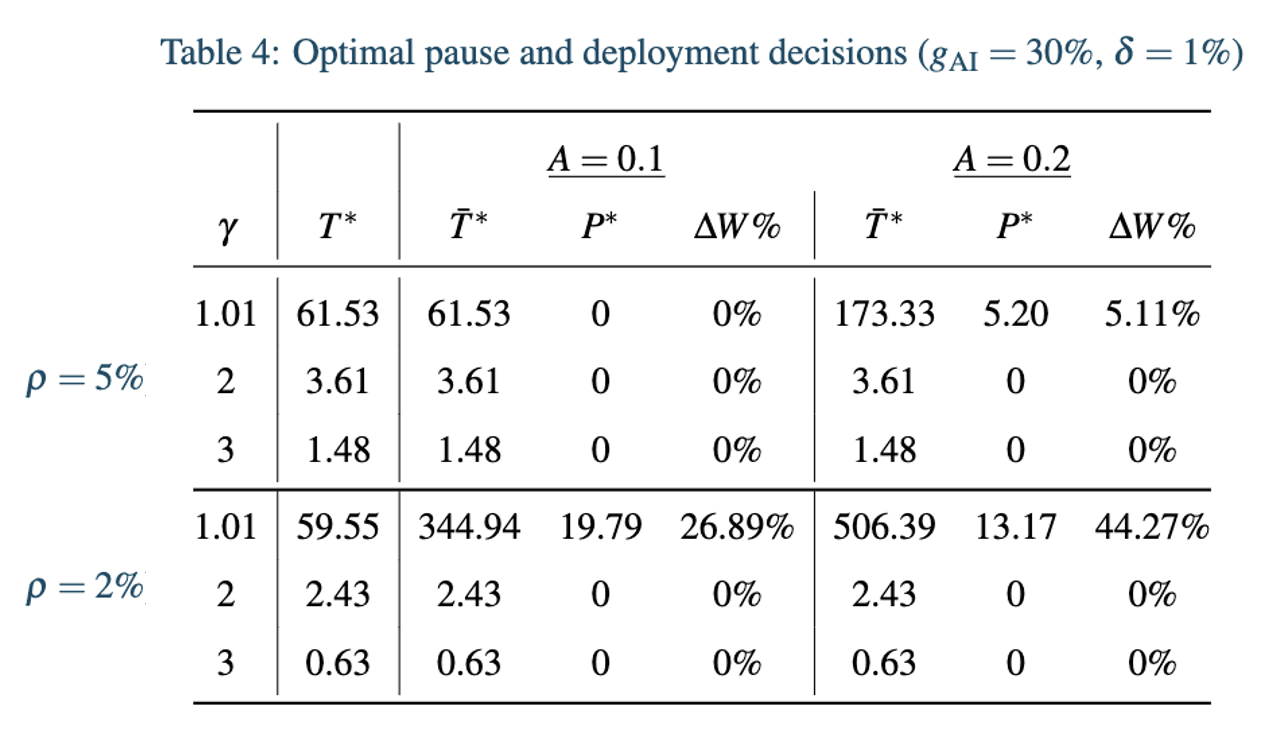
As above, is the percent change in welfare after the optimal pause and deployment decision, relative to optimal timing decision where there is no possibility of pausing. Here the ability to choose our pause time means that the optimal decision can never reduce welfare compared to the business-as-usual growth path.
As we can see here we need both quite fast decline in existential risk from AI during pause time and either relatively weakly diminishing returns to consumption or a low discount rate to justify any pause at all. In the case where , a 5 year pause takes the annual existential risk from deployed AI from 1% to 0.6%, and the 13 year pause takes this value to 0.27%, which is why AI is deployed for so long after the pause window in the table above. We can see that a lower discount rate has quite a dramatic impact by scaling up the time spent in the pause period since it decreases the losses associated with long pause periods and increases the gains from enjoying high economic growth after the pause period. We can also see that this change in the discount rate only influences the decision to pause in low calibrations of .
Reducing the discount rate even further generally follows the same pattern of effect. With (relative to ) and , it is optimal to pause for longer, and then run the AI for longer; and with or it still isn't optimal to pause at all under the calibrations of considered.
Some additional thoughts.
Of course there may be many reasons why we may want to pause that are not considered in this simple model, including uncertainty and political realities. For example, I think attention could be given to optimal pause decisions when we are uncertain of whether AI is risky or safe; pausing in this context may allow us to collect additional information about whether to deploy the AI at all (Acemoglu & Lensman (2023) offer some analysis of information considerations in the context of adoption of risky technology). Further, merely pausing is unlikely to deliver safer AI (as I have assumed). A pause should come hand-in-hand with investments in AI safety to have any influence on the existential risk of the model eventually deployed. Further extensions to this model could consider optimal investment of current resources into AI safety research alongside a pause to allow for differential technological progress.
A final point is that any economic model attempts to boil down some, often complex, phenomena to something that can be studied with relatively standard methods. If one were to try and write down a comprehensive economic model of whether we should deploy AI models and which models should be deployed, I expect they could come up with quite different quantitative results than those reported above.
III. Conclusion
Despite the considerations left out of this extension, I hope that these results may clarify the impact of at least some relevant considerations when it comes to the decision to pause in the face of potential growth and existential risk. I think there is room for further work in this area. As mentioned above, a potentially interesting extension would be considering optimal pause decisions where we are uncertain about how risky AI is; due to the irreversibility of existential risk, pausing may preserve option value.
I hope that some of the simple results derived by Jones may help to calibrate some heuristics EAs might use to consider at least part of the problem of balancing the promise and threat of AI. Further, I hope that the extensions I consider can a). clarify how robust these simple heuristics are to non-AI growth considerations and b). provide some inspiration for doing more research on the welfare implications work that reduces existential risk from AI and/or delays deployment of advanced AI models.
- ^
I'd like to thank Gustav Alexandrie, Dan Carey, John Firth, Jojo Lee and Phil Trammel for comments on drafts of this post.
- ^
From a relatively quick google, the White House has recently endorsed a 2% discount rate, while the UK has endorsed a 3.5% rate (for valuing the first 30 years of a project).
- ^
Here we call log utility the case of constant relative risk aversion utility when the curvature parameter equals 1, because as this variable approaches 1, we have.
- ^
Here I am just using welfare to refer to some aggregation of utilities of individuals over time.
- ^
Starting with , to put this in dollar terms we can divide this value by and then divide again by to put in terms of the value of life relative to the consumption available to people today. Therefore
- ^
Trammel (2023) makes the point that calibrating this parameter in this way may have some questionable implications in the context of long-term changes in welfare. As society progresses we develop new products (medicines, foods, electronics). We might expect that someone with infinite wealth now can live a better life than someone with infinite wealth 1,000 years ago because of access to these new products. One way of modelling this access to new products would be to have rising over time so that our utility is bounded according to the products we have access to.
- ^
In this set-up, if we face a 1% risk of extinction each year (from non-AI sources) this will be functionally equivalent to discounting the future by 1% a year: if there is a 99% chance of us being alive next year then 1 unit of welfare next year is equal, in expected terms, to 0.99 units of welfare today.
- ^
Infamously, in expected value terms taking repeated 50/50 gambles at extinction or doubling (plus a tiny amount) total welfare will always be worth it.
- ^
For more details on the implications of an individual vs social discount rate, Eden (2023) offers an interesting analysis.
- ^
As a bonus result, setting , Jones gives us an analytical example of how will come out if AI delivers a singularity and delivers mortality improvements with a bounded utility function. Suppose the AI increases our life-expectancy to times our original life expectancy (), then we have the cut-off risk:
For example, if our current life expectancy is 100 years and AI doubles this (so ; as is the case if AI reduces annual mortality risk from 1% to 0.5%) and individuals tend to discount their own lives at 1% per year, then this (very impressive) AI that delivers a singularity a huge longevity benefits should be deployed so long as the total risk of extinction is less than 25%. This gives some intuition for why the above results for cut-off risks for or in Table 1 seem to approach 25%.
- ^
One could also just write down a different model, different from the Jones model (see Damon Binder's model of AGI deployment), but at least part of my hope of extending on the Jones model is that this can identify any (quantitative) limitations in the model Jones proposes.
- ^
Here I use a calibration term of 1.01 rather than 1 to avoid having to define an additional (log) utility function, though the results will be quite similar. I use Matlab to optimize this welfare function (and all other examples in this section). The script can be found here.
- ^
Though longtermists may generally discount at a much lower rate than this.

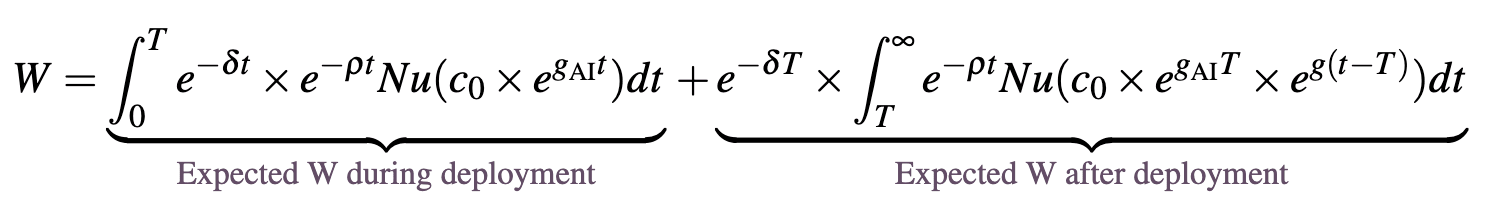
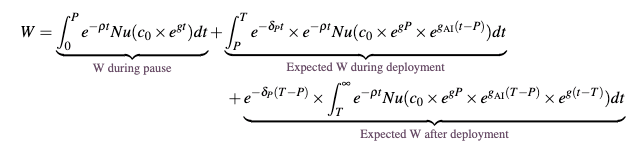
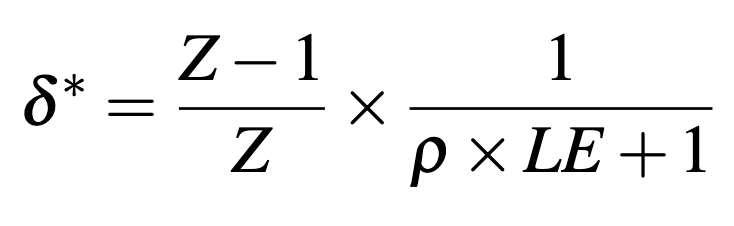
Executive summary: The decision to deploy AI that could increase both economic growth and existential risk depends critically on the potential growth benefits, the existential threat, and the curvature of the utility function, with extensions showing that economic growth outside of AI deployment and the ability to pause AI to reduce risk can significantly impact optimal deployment decisions.
Key points:
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.