One of the key tenants of longtermism is that human life has the same value temporally. That is, a child born in 1930 has the same “worth” as a child born in 2020.
One very relevant story then, is from the book/movie, Sophie's Choice, where the main character, Sophie, is sent to Auschwitz with her two children. The Germans there tell Sophie she has a choice between saving one child over the other. As the Germans are tearing her children away from her, she grabs one child and makes the decision, while the other is sent to the crematorium.
Longtermists face a similar dilemma between prioritizing a child today and a child in the long term future. The question this begs, then, is that if an EA time traveler were to be given Sophie’s choice of choosing between saving the child born in 1930 versus saving that child’s great grand-daughter, born in 2020, then would the time traveler be morally indifferent between the two? Many longtermists say “yes”.
On the other hand, most projects, including climate change mitigation, development grants, etc. rely on a tool called discount rates, where taking action in the present is more valuable than taking action in the future. In personal finance, this is because if I invest one dollar into a treasury bond today, then I will get a certain bigger amount of money in 25 years. Thus, when evaluating whether I ought to spend money on one project versus another, I would use a math formula to “reduce the value” of future money. The number I multiply future money with to make it smaller is called the discount rate. Another word for “discount rate” is “risk free rate” or “risk free return”—they all mean the same approximate thing.
Now, many longtermists argue that this analogy to personal finance is improper. Longtermists argue that “absent catastrophe, most people who will ever live have not yet been born”, and some argue that the social discount rate ought to be zero (a person in the future has the same moral worth as a person today). At first blush, this seems perfectly logical—after all, lives are different than money, and we should not make such a comparison lightly.
Nevertheless, here, I argue that the social discount rate cannot be zero; in fact, making it zero would lead to some wild conclusions (a proof by contradiction). I then argue that a reasonable estimate of the social discount rate ought to be tied to our predictions about fertility and is around 0.065. And I conclude by arguing that more EA funding should thus go to solving more temporally pressing problems such as global poverty.
Argument 1: the social discount rate cannot be zero.
If we continue as we are, there will potentially be infinite numbers of future humans. It’s plausible that under current technological progress, babies continue to be born, we somehow escape the solar system, and the universe continues expanding infinitely—and humans with it. Under a zero discount rate, the social value of a project is the sum of future people (as opposed to the discounted sum total of future people). As long as babies are born, we will continue adding integer numbers of people onto this sum. This sum will never converge, the sum of all future human lives will be infinite, just by population growth.[1]
Or, in math: let be the social discount rate, and be the year. The potential benefit of a project that saves lives is
Contradiction 1:
Then, consider the bizarre scenario where a random person on the street, let’s call him Alfred Ingersoll, tells you, “I am Alfred Ingersoll, the destroyer of worlds; give me all your money, or I will make a technology that will make humanity extinct in 1000 years.”[2] A longtermist would then perform the expected utility calculation:
The probability that Alfred Ingersoll is telling the truth is not zero, simply because with almost all things, there’s a tiny tiny chance that he’s telling the truth. But the right hand side, the number of people he could kill if he succeeds, is countably infinite. And if we multiply a tiny tiny number by infinity, we get…welp, infinity. So, this equation becomes:
Thus, since the expected benefit is infinite, a zero discount rate longtermist would opt to give Alfred Ingersoll (let’s abbreviate his name to A.I.) all his or her money. But this is a contradiction, because no reasonable person would give all of his or her money to a random person that just says this single sentence.
Contradiction 2:
And there’s more—a longtermist with a zero discount rate is indifferent between all projects that consistently save lives every year. Let’s say I had two projects: one that saves 1 life every year, and another that saves 500 million lives for the first 100 years, but then from the 101st year onward, also saves 1 life every year. The average logical person would prefer the second project. But the zero discount rate longtermist would be indifferent between the two, because both projects save infinite numbers of lives.
Contradiction 3:
Another potential problem with having a zero social discount rate is what it ends up doing to investments in obviously good things. If we truly believe that a life saved today is the same value as a life saved tomorrow, then our approach to philanthropy (in regards to GiveWell, Open Philanthropy, FTX Future Fund) would be to save the money, invest it into something that does compound, and spend it later, when we have more technologically advanced capabilities. Case in point—don't invest in malaria bed nets now, because in 20 years time, we will a) have more money to invest b) have a new vaccine that is way cheaper and easier to distribute (one that isn't 4 shots). The cost effectiveness of our donation money would be far greater than it is today. For non-catastrophic dangers like malaria, a zero discount rate longtermist would almost always opt to delay spending. He or she would have no urgency at all.
Since we have a contradiction, there must be something about the previous claims we’ve made that is false. And I argue that it is the zero discount rate. This sum of the social value of giving A.I. all your money, must be finite. The present value calculation must converge to a number. It is probably better to prioritize the project that saves 500 million lives for 100 years, and we all agree that initiatives that focus on persistent but non-existential harms like global health are important. The social discount rate must be a positive nonzero number.
Okay, so that’s my first argument, and one that I hope is not too controversial. I expect only the hardline longtermists will be upset that the discount rate is not zero; most longtermists will be perfectly comfortable arguing that sure, the discount rate is not zero, but maybe it’s also a tiny tiny number. Who cares!
Now, onto the second argument.
Argument 2: a reasonable estimate of the social discount rate ought to be tied to our predictions about fertility and is above 0.065
Now, I began this essay by saying that if the time traveler were to be given the choice of choosing between saving the child born in 1930 versus saving that child’s great grand-daughter, born in 2020, then the time traveler would be indifferent between the two.
But, one obvious counter is—if the time traveler did not save the child born in 1930, then all the future descendants of this person would not exist! And if the child born in 2020 was the great grand-daughter of the child born in 1930, then by not saving the child born in 1930, the counterfactual is that the child in 2020 is gone already.
Of course, this gets into population ethics—if the time traveler did not choose to save the person in 1930, then maybe we don’t care about that person’s potential grandchildren; this is called having “person-affecting” views, because we only care about people that do exist. But most longtermists do not have person-affecting views, and so since I am trying to convince a longtermist crowd, I will presume that you too, reader, do not have person-affecting views.
Thus, if I save someone today, that person will, on average, give birth to 2.4 people. Their children will then have children, and so on and so forth. Thus, saving a life today is more important than saving a life 90 years from now, because population compounds.
Moreover, quality of life generally has been improving. So, helping someone in 1930, during the throes of the Great Depression, is going to be way more important than helping someone in 2008, during the Great Recession, because the people in the more recent period have better coping mechanisms (access to food and sanitation or a better monetary and fiscal system, for example).
So, at bare minimum, a lower bound on the social discount rate ought to be linked to population growth and our expectations of fertility. One could imagine a more sophisticated social discount rate that also took into account quality of life improvements, but that would only raise the social discount rate.
And let’s take a look at where fertility is going:
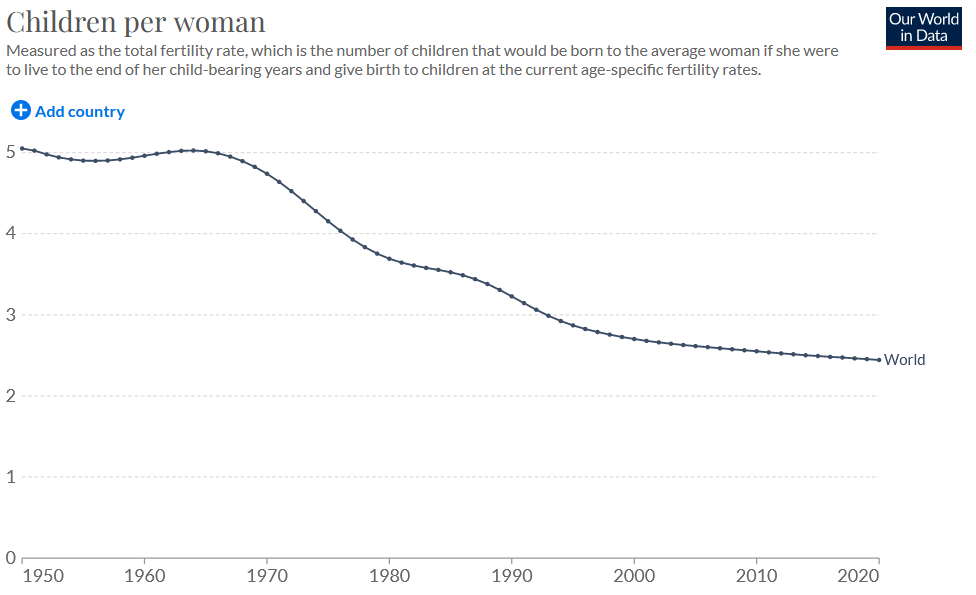
It seems to be stabilizing around 2.4 globally. Each generation is around 25 years (time between grandparents to parents).
A naïve estimate of the discount rate:
So, the above logic makes me quite indifferent between saving a life now and saving 2-3 lives 25 years from now.[3]
If we say that in 25 years, the original person we saved has a life expectancy that is around three quarters of their original life expectancy, then a naïve calculation of the social discount rate goes as follows:
Or, more generally,
Where is the fertility rate (NOT a function), is the social discount rate, is the fraction of the remaining life expectancy of the original person we saved, and is the time between generations.
We assume that the original person we are saving is a fertile female. We divide the fertility rate by two as a rough approximation for the chance of giving birth to a male (and therefore that person being unable to give birth to future people). Unlike most of history, male offspring in my calculation have 0 social worth. But, including men would once more, increase the estimate.
Solving this equation, we get:
So, plugging in (fertility rate), (time between generations), (remaining life expectancy), we can solve for a back-of-the-envelope estimate of .
Okay, so a naïve lower bound estimate of the social discount rate is 0.065.
Then, this means that if I had the option between saving 1 life now and 1+0.065 lives next year, I’d be indifferent between the two options.
Argument 3: more EA money should go to development.
Now, onto the applications. Let’s say that you are an EA organization, and you have the option of choosing between funding a portfolio that saves 1 million people each year, or a project that saves 5 billion people 100 years from now.
We can now model this using discounting:
The first project would give us a “present value” (PV) of:
The second project gives us:
That is, the first project will give us an present value of 14.7 million lives saved, while the second gives us a present value of 9.2 million lives saved. So, the first project would be equivalent to saving 14.7 million lives today, and the second to saving 9.2 million lives today. The first project is better.
And this is assuming that we don’t make it to Mars, that quality of life is the same, and that life expectancy stays the same—all of which would increase the discount rate![4]
Ultimately, what I’m arguing for is not that we ignore catastrophic tail risks (or X-risks)—far from it. I think any reasonable philanthropic portfolio of good projects would include a portion where we hedge for tail risks, especially since they often end up being neglected by the rest of society. And in fact, if the tail risk has a high chance of occurring in the next 100 years, then it could be very effective to work on it. Moreover, many claims of X-risk don't rely on strong assumptions about zero discount rates.
But I fear that the longtermist community, and by association the EA community, has become so fixated on catastrophic risks that we’re shuttling exorbitant amounts of energy and resources towards projects that ultimately have little impact.
There are things we can do now, like road safety, global skills partnerships, building administrative data infrastructure, and training poorer country bureaucrats, which we know help people, save lives, and improve growth.
We are all time travelers, and we have the choice between saving a child in now versus a child in the long-term future. But let there be no moral ambiguity—save lives now, not later.
TLDR
Medium TLDR: The social discount rate cannot be zero. Under non-person affecting views (which most longtermists ascribe to), a reasonable estimate of the social discount rate ought to be tied to our predictions about fertility and is above 0.065. Given this discount rate, more EA money should go to development because long term risks are overblown.
Super short TLDR: If longtermists don’t hold person-affecting views, then shouldn’t they discount the future based on population growth?
Appendix
Here are some ideas that I haven’t fully thought through:
- Perhaps present value is the wrong way to think about tail risk at all.
- The total funding to AI prevention / long term risks is ~24% of total EA funds (post-FTX). This may be small in the grand scheme of global (non-EA included) charitable giving. (my calculation via adding on FTX Future Fund and a guesstimate of how much they're spending on long term risk onto Benjamin Todd’s estimates of EA giving)
| Cause Area | $ millions per year in 2019 | % | long term existential threat projects? | |
| Global health | $185 | 36% | 0% | |
| Farm animal welfare | $55 | 11% | 0% | |
| Biosecurity | $41 | 8% | 0% | |
| Potential risks from AI | $40 | 8% | 100% | |
| Near-term U.S. policy | $32 | 6% | 0% | |
| Effective altruism/rationality/cause prioritisation | $26 | 5% | 0% | |
| Scientific research | $22 | 4% | 0% | |
| Other global catastrophic risk (incl. climate tail risks) | $11 | 2% | 100% | |
| Other long term | $2 | 0% | 100% | |
| Other near-term work (near-term climate change, mental health) | $2 | 0% | 0% | |
| FTX future fund | $100 | 19% | 70% | |
| Total | $516 | 100% | 24% | $123 |
[1] Do not be confused between the total population in the world (which may level off) and the sum of all people that will ever exist (which is potentially infinite).
[2] I read a less-rigorous version of this argument somewhere on Wikipedia, but either it has been edited away, or the original article eludes me.
[3] Note that I consider a female life here—male lives are less valuable, as humanity could continue to give birth with a limited population of males. That is why I do not set the left hand side equal to 2 (mother and father), but only 1 (mother).
[4] This is because if people make it to Mars, I think they’d make more than 2.4 babies on average.

Thanks for posting! I think you raise a number of interesting and valid points, and I'd love to see more people share their reasoning about cause prioritization in this way.
My own view is that your arguments are examples of why the case for longtermism is more complex than it might seem at first glance, but that ultimately they fall short of undermining longtermism.
A few quick points:
Hi Max,
Thanks so much for responding to my post. I’m glad that you were able to point me towards very interesting further reading and provide very valid critiques of my arguments. I’d like to provide, respectfully, a rebuttal here, and I think you will find that we both hold very similar perspectives and much middle ground.
You say that attempting to avoid infinities is fraught when explaining something to someone in the future. First, I think this misunderstands the proof by contradiction. The original statement has no moral bearing or any connection with the concluding statement—so long as I finish with something absurd, there must have been a problem with the preceding arguments.
But formal logic aside, my argument is not a moral one. But a pragmatic and empirical one (which I think you agree with). Confucius ought to teach followers that people who are temporarily close are more important, because helping them will improve their lives, and they will go on to improve lives of others or give birth to children. This will then compound and affect me in 2022 in a much more profound way than had Confucius taught people to try to find interventions that might save my life in 2022.
Your points about UN projections of population growth and the physics of the universe are well taken. Even so, while I do not completely understand the physics behind a multi-verse or a spatially infinite universe, I do think that even if this is the case, this makes longtermism extremely fraught when it comes to small probabilities and big numbers. Can we really say that the probability that a random stranger will kill everyone is 1/(total finite population of all of future humanity)? Moreover—the first two contradictions within Argument 1 rely loosely on an infinite number of future people, but Contradiction 3 does not.
The Reflective Disequilibrium post is fascinating, because it implies that perhaps the more important factor that contributes to future well-being is not population growth, but rather accumulation of technology, which then enables health and population growth. But if anything, I think the key message of that article ought to be that saving a life in the past was extremely important, because that one person could then develop technologies that help a much larger fraction of the population. The blog does say this, but then does not extend that argument to discount rates. However, I really do think it should.
Of course, I do think one very valid argument is whether technological growth will always be a positive force for human population growth. In the past, this seems to be true. As, it seems that these positive technologies vastly outweighed the negative effects of technology on the ability to wage war, say. The longtermist argument would then be, that in the future, the negative effect of technology growth on population will outpace the positive effect of technology on population growth. If this indeed is the argument of longtermists, then adopting a near zero discount rate indeed may be appropriate.
I do not want to advocate for a constant discount rate across all time for all projects, in the same way that we ought not to assign the same value of a statistical life across all time and all countries and actors. However, one could model a decreasing discount rate into the future (if one assumes that population growth will continue to decline past 2.4 and technological progress’s effect on growth will also slow down) and then mathematically reduce that into a constant discount rate.
I also agree with you that there are different interventions that people could do or make at different periods of history.
I think overall, my point is that helping someone today is going to have some sort of unknown compounding effect on people in the future. However, there are reasonable ways of understanding and mathematically bounding this compounding effect on people in the future. So long as we ignore this, we will never be able to adequately prioritize projects that we believe are extremely cost-effective in the short term with projects that we think are extremely uncertain and could affect the long term.
Given your discussion in the fourth bullet point from the last, it seems like we are broadly in agreement. Yes, I think one way to rephrase the push of my post is not so much that longtermism is wrong per se, but rather that we ought to find more effective ways of prioritizing any sort of projects by assessing the empirical long-term effects of short-term interventions. So long as we ignore this, we will certainly see nearly all funding shift from global health and development to esoteric long-run safety projects.
As you correctly pointed out, there are many flaws with my naïve approach calculation. But the very fact that few have attempted to provide some way of thinking about different funding opportunities across time seems very flawed.
Thanks! I think you're right that we may be broadly in agreement methodologically/conceptually. I think remaining disagreements are most likely empirical. In particular, I think that:
(I think this is the most robust argument, so I'm omitting several others. – E.g., I'm skeptical that we can ever come to a stable assessment of the net indirect long-term effects of, e.g., saving a life by donating to AMF.)
This argument is explained better in several other places, such as Nick Bostrom's Astronomical Waste, Paul Christiano's On Progress and Prosperity, and other comments here and here.
The general topic does come up from time to time, e.g. here.
In a sense, I agree with many of Greaves' premises but none of her conclusions in this post that you mentioned here. I do think we ought to be doing more modeling, because there are some things that are actually possible to model reasonably accurately (and other things not).
Greaves says an argument for longtermism is, “I don't know what the effect is of increasing population size on economic growth.” But we do! There are times when it increases economic growth, and there are times when it decreases it. There are very well-thought-out macro models of this, but in general, I think we ought to be in favor of increasing population growth.
She also says, “I don't know what the effect [of population growth] is on tendencies towards peace and cooperation versus conflict.” But that’s like saying, “Don’t invent the plow or modern agriculture, because we don’t know whether they’ll get into a fight once villages have grown big enough.” This distresses me so much, because it seems that the pivotal point in her argument is that we can no longer agree that saving lives is good, but rather only that extinction is bad. If we can no longer agree that saving lives is good, I really don’t know what we can agree upon…
I think infinite humans are physically impossible. See this summary: https://www.fhi.ox.ac.uk/the-edges-of-our-universe (since the expansion of the universe is speeding up, it's impossible to reach parts that are expanding faster that light speed, thus we only have a huge chunk, but not all of the universe we can access)
I really like this post. I totally agree that if x-risk mitigation gets credit for long-term effects, other areas should as well, and that global health & development likely has significantly positive long-term effects. In addition to the compounding total utility from compounding population growth, those people could also work on x-risk! Or they could work on GH&D, enabling even more people to work on x-risk or GH&D (or any other cause), and so on.
One light critique: I didn't find the theoretical infinity-related arguments convincing. There are a lot of mathematical tools for dealing with infinities and infinite sums that can sidestep these issues. For example, since ∑∞t=1f(t) is typically shorthand for limt→∞∑tx=1f(x), we can often compare two infinite sums by looking at the limit of the sum of differences, e.g., ∑∞t=1f(t)−∑∞t=1g(t)=limt→∞∑tx=1(f(x)−g(x)). Suppose f(t),g(t) denote the total utility at time t given actions 1 and 2, respectively, and f(t)=2g(t). Then even though ∑∞t=1f(t)=∑∞t=1g(t)=∞, we can still conclude that action 1 is better because limt→∞∑tx=1(f(x)−g(x))=limt→∞∑tx=1g(t)=∞.
This is a simplified example, but my main point is that you can always look at an infinite sum as the limit of well-defined finite sums. So I'm personally not too worried about the theoretical implications of infinite sums that produce "infinite utility".
P.S. I realize this comment is 1.5 years late lol but I just found this post!