Weight by Impact

There’s an old idea in decision theory that I want to explore some nuances of. I don't think any of this is original to me. I assume basic familiarity with manipulating probability distributions and calculating expected values, but feel free to ask questions about that.

Decision-making under uncertainty often involves scenario analysis: take a broad uncertainty you have, split it into scenarios, and then consider the scenarios individually. For example, you might be uncertain how likely humanity is to succeed at aligning AI systems, and then find it useful to think separately about scenarios where the problem is easy enough that success is near-guaranteed (hereafter ‘easy’), difficult enough that failure is near-guaranteed (hereafter ‘hopeless’), or in the middle of the logistic success curve, where things could go either way (hereafter ‘effortful’).

In terms of return for further thinking or effort spent on impacting scenarios, it seems clear that the effortful scenario, where things could go either way, presents more opportunity than the other two. If success is already guaranteed or denied, what’s the point of additional consideration? So planners will often condition on the possibility of impact (see also “playing to your outs”, which is a closely related idea).

I think this is half-right, and want to go into some of the nuances.

Conditioning vs. Weighting

I think you should weight by impact instead of conditioning by impact. What does that mean?

I think the main component is separately tracking impact / tractability and plausibility so that you don’t confuse the two, can think about them separately, and then join them together.

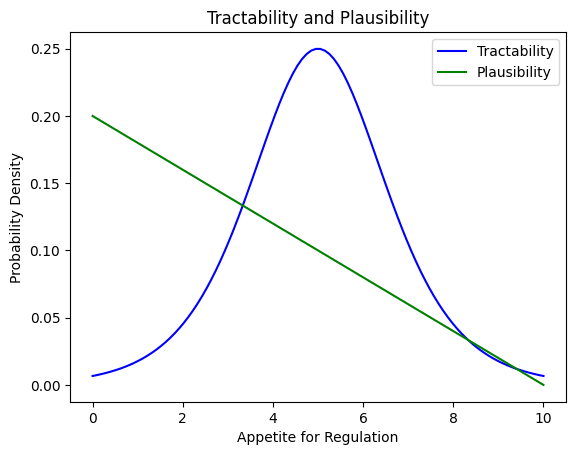
For example, suppose there’s some continuous variable, like “appetite for AI regulation”, that you model as ranging from arbitrary units 0 to 10, with lower values as more plausible (you model this as a simple triangular distribution.) and middle values as more tractable (too little appetite and any regulation passed will be insufficient, and too much appetite and default regulation will handle it for you; you model this as having a cdf that’s a logistic curve with a scale of 1.5).

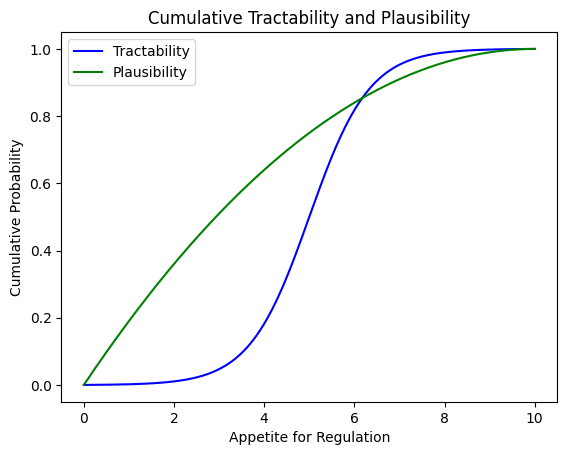
This then generates two pictures:

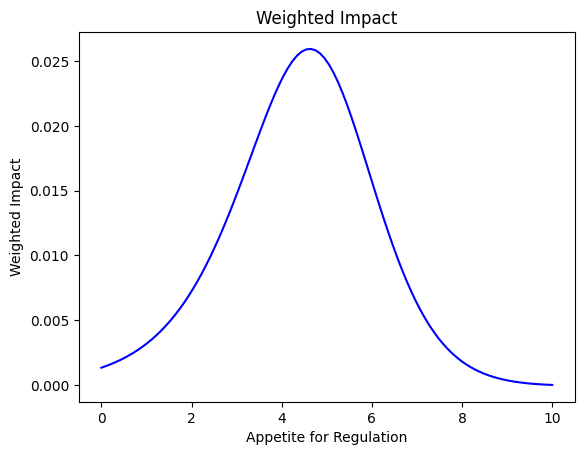
When combined, the resulting distribution (of ‘weighted impact’ for each possible value of ‘appetite for regulation’) is not symmetric, but counts both plausibility and tractability.

For this particular numerical example, the difference applies mostly in the tails (notice that the left tail is substantially thicker than the right tail) but also matters for the mode (it’s shifted left from 5 to about 4.6). If the background distribution for the independent variable (appetite for regulation) had been more concentrated, it would have had an even more noticeable effect on the final impact-weighting (and presumably implied planning for a much narrower slice of overall probability).

Why does this matter? It restores the continuous view, not just thinking about the worlds where you matter most, but the range of worlds where you have some influence. When the underlying uncertainty skews in one direction, that skew is preserved in the final result. (When just focusing on the tractability distribution, for example, you might think variation in both directions leads to similar decreases in tractability, but that doesn’t imply both are equally important for weighted impact!)

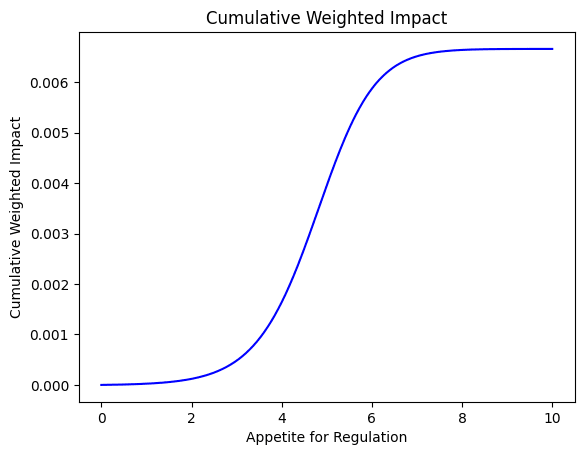
It also makes the 'penalty' of the model more legible--in this example, two thirds of the available impact happens when the variable is between 4 and 6, which only happens 20% of the time. 

Don’t Lose Sight of Reality

In Security Mindset and the Logistic Success Curve, Eliezer depicts a character who finds herself frequently conditioning on impact, which means her conjunctive mental world might be quite different from the real world she finds herself living in. To the extent that having impact requires reality-based planning, this move can’t be used many times before it itself cuts into your possibility of impact.

As well, you might be confused about some important facts of the world which mean your original sorting of individual possible worlds into categories (easy, hopeless, and effortful) could be incorrect. Spending time exploring scenarios that seem irrelevant, instead of just exploiting scenarios that seem relevant, can help catch these mistakes and might end up dramatically shifting one’s efforts. (If most of your effort had been focused on a 5% world that had high tractability, and a 10% world suddenly becomes tractable, you might drop all of your previous efforts to focus on the one that’s now twice as impactful.)

Impact vs. Other Concerns

“Condition on impact” and “play to your outs” both focus on how to win. But if you have multiple concerns beyond winning, then the overall probability of winning matters for making tradeoffs between those concerns. Considering someone playing a card game, resigning can’t ever improve their chances of winning the match that they’re currently playing, but it can help with their other goals, like conserving calories or spending their time doing something they enjoy. As winning becomes less and less plausible, resigning becomes more and more attractive.

Weighting by impact helps put everything in your shared currency, whereas conditioning implicitly forgets the penalty you’re applying to your plans. In the card game, the player might price a win at $100 and the benefits of resigning early at $1, and thus resign once their probability of winning is less than 1%. Getting tunnel vision and attempting to win at the game at all costs might end up with them losing overall, given their broader scope.

For most situations, doing the accounting correctly leads to the expected outcome, so this will only sometimes be relevant. But when it is relevant, it’s useful, and having the losses from ignoring a wide swath of probability-space be counted in the expected value of actions seems more honest.