This post briefly explores the implications population density might have for wild animal welfare and some considerations for the plausibility and potential impact of population control as a welfare intervention. It was originally published on the Wild Animal Initiative blog, here.
Introduction
Largely as a result of human development, the sizes of many wild animal populations have been falling.[1] Much of this decline has resulted not from direct killing of wild animals by humans, but indirectly by fragmenting their habitats and cutting animals off from the resources that sustained their historical population sizes.[2][3] This has immediate consequences for the welfare of individuals, who may face starvation, competition for resources, or conflict with humans as they try to access resources in their former habitat (e.g. urban pigeons[4]; fur seal[5]; black bear[6]). According to many ethical views, it is better to have more happy animals than fewer equally happy animals; but as a population grows, so does the number of individuals who may be adversely affected by further growth, requiring us to think carefully about trade-offs between the quantity and quality of welfare. A thorough understanding of individual welfare levels in a given population and how they are affected by changes in population density could eventually enable us to estimate the population size which would maximize the welfare experienced in that population.
Population modeling and density-dependence
The density of a population is defined by the ratio between the number of individuals and the amount of habitat or a limiting resource available to them; if a population grows or its habitat declines, population density increases. The population size (N) at which a balance between birth rate and death rate is achieved—its maximum sustainable size—is known as the “carrying capacity” (K) under given environmental conditions (Box 1).
Box 1
A population’s growth rate per generation (r) is equal to the difference between the number of births (b) and the number of deaths (d): r = b - d. The growth rate before any effects of density are taken into account is denoted r₀. To the extent that r₀ exceeds zero, density-dependent effects must reduce age-specific survival or fecundity rates to achieve a stable population. The population size (N) at which r = 0 and the population remains stable long-term is known as the carrying capacity (K).These parameters come together in the logistic growth equation, where any excess of births over deaths shrinks to zero as N approaches K: dN/dt = r₀N(K - N)/(K). While this equation captures how extremes of population density relate to population growth rates, it is certainly incomplete. For example, intermediate densities may have less consistent effects than the simple logistic function suggests, especially in populations facing strong density-independent stressors. Populations inhabiting an environment that changes much more rapidly than the time between their generations may never reach their carrying capacity at any given time, but may still encounter strong density effects during periods when N > K, as might occur during a drought or similar period of low productivity.
Death rates may rise and birth rates may fall as a result of stressors experienced by the animals in a population. These stressors can be density-dependent or density-independent. For example, competition for food can lead to starvation and limit the energy available for reproduction[7], and crowding in early life can cause an animal to age prematurely[8]. Infectious diseases may also spread more rapidly in a dense population[9].
Other causes of mortality are density-independent. In a river, water temperature or pollutants might kill fish at a rate that is independent of the number of fish in the river[10]. Indeed, density-independent factors can make an environment so hostile that the maximum stable population size is very low, and the surviving individuals face no meaningful competition for resources.
Whether a certain factor is density-dependent or density-independent can also vary according to the circumstances. For example, the direct threat posed to any individual by fierce winds and lightning during a storm is independent of density, but density-dependent mortality might follow in the wake of the storm if a limiting resource has been damaged. Population density within a certain range can also have positive effects for individual welfare by providing safety in numbers and more accessible social interactions. For example, having fellow newts around during their transition to maturity means that individuals of Triturus cristatus are less likely to undertake dangerous migrations to find mates[11].
Welfare implications of population density
In a recent article, I proposed the concept of welfare expectancy as a way to link age-specific survival rates and welfare. Welfare expectancy is a sum of the lifetime welfare an individual born into a given population can expect to experience. Age-specific survival rates may also be correlated with age-specific welfare, suggesting that any density-related impairment of survival could greatly reduce welfare expectancy, especially when it affects juvenile animals.
A general expectation of declining welfare expectancy per individual as a population grows towards its carrying capacity raises the possibility that the population size which maximizes the total welfare of a population may be smaller than its maximum sustainable size. Whether this occurs depends on how many individuals the population would contain at its carrying capacity and how average welfare varies with population size (Box 2). The conditions are most likely to be met if the strongest negative effects of population density on welfare manifest at high densities (i.e., as N approaches K; Figure 1). This could occur under the following three conditions:
- if lower densities primarily limit reproduction while higher densities affect survival rates.
- if density-dependent mortality disproportionately affects older animals at lower densities but young animals at high densities; or
- if density-independent effects are nearly sufficient to stabilize the population’s growth rate, so any negative effects of density are only felt near the carrying capacity.
In general, the shape of average welfare expectancy with respect to density depends on the particular ecology and life history of the population in question, especially whether density preferentially affects fecundity versus survival rates or the survival rates of young versus old individuals. If increased density is mainly accommodated by reduced fecundity or late-life survival, for instance, then average welfare might not decline so steeply as a population grows. Theory and reviews of demographic models for a variety of large vertebrates suggest that juvenile survivorship is usually the first casualty of high population densities[12][13][14], which is one set of conditions under which we might expect the welfare-optimal population density to be lower than the population’s carrying capacity. Part of the explanation for this pattern in large vertebrates is the competitive advantage older animals typically have over younger animals who are smaller and less experienced. However, it is not yet known how broadly these age dynamics apply among the much more numerous smaller-bodied, “fast-living” animals, where there are examples of adult advantage[15] and disadvantage[16]. More research is needed into the expected shape and mechanisms of density-dependence among their populations.
Box 2
Let Wₙ represent the average welfare expectancy at population size N and let K represent the population size at carrying capacity. Then, the welfare-optimal population size will be less than the carrying capacity if Wₖ₋₁/Wₖ > K/(K - 1).The welfare expectancy per individual in a population depends on the life expectancy from birth and the welfare they typically experience over that lifespan. If average welfare is positive, average welfare expectancy will correlate with life expectancy. If an increase in population density disproportionately harms the youngest animals, this can greatly reduce life expectancy.
Implications for welfare interventions
If we are completely uncertain about the absolute welfare level of animals in a population, then it follows that we are completely uncertain about whether their lives are dominated by pleasure or suffering. If their lives contain more goodness on average, then increasing the population size would be expected to increase the total amount of welfare experienced within the population as a whole. On the other hand, if their lives are primarily unhappy, then adding more unhappy individuals through population growth would actually subtract from the population’s total welfare. From a standpoint of complete uncertainty, then, the expected value of population growth or decline is symmetrical[17]. Whether or not population growth increases or decreases total welfare of the population depends on the balance of the positive and negative experiences of the individuals added by that growth.
However, the existence of a density-dependent decline in average welfare would set up an asymmetry in favor of relatively smaller populations, since increasing population density would reduce the probability that average welfare remains net-positive, giving population growth a lower expected value than population reduction. Of course, this heuristic assumes complete ignorance of the population’s welfare characteristics, which is rarely the case.
On the other hand, if we knew the exact average welfare expectancy for all possible population sizes (Wₙ), we could predict its optimal density and also define a ‘margin of error’ on either side within which total welfare expectancy would be expected to at least equal that obtained at carrying capacity (Figure 1). This could provide a wide target for interventions aiming to improve welfare by managing population density. Notably, the largest range and scope for improvement in total welfare over what would occur naturally is possible when the most aversive effects of population density only manifest at high densities. This suggests that a review of evidence on the shapes of density-dependence curves for various species could indicate how impactful managing around population density might be as a form of welfare intervention.
Figure 1
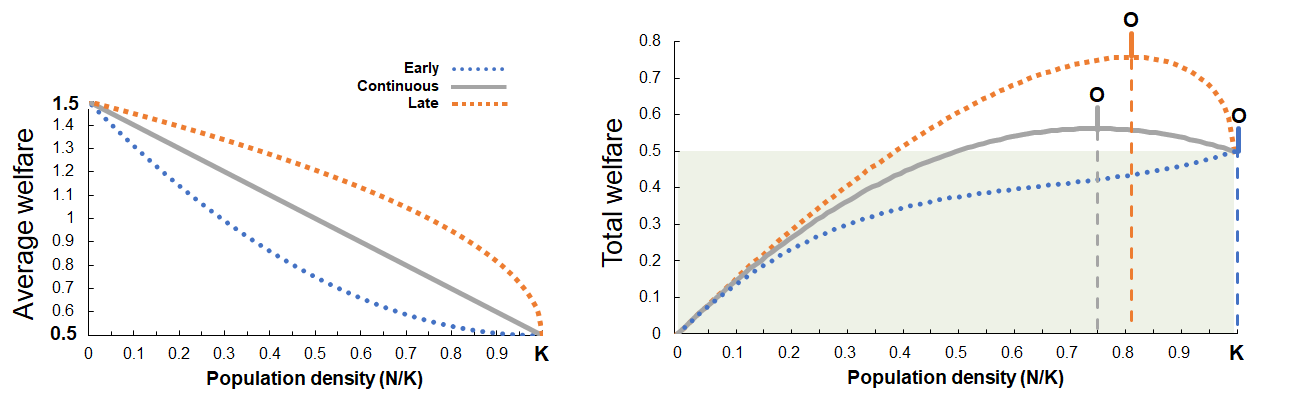
Left: Hypothetical curves depict how average (per-individual) welfare expectancy might decline with increasing population density, depending on whether the most aversive effects of density develop at low densities (“early” in population growth), at a constant rate (“continuous”), or only at high population densities (“late”). Right: Average welfare under each of these three scenarios is multiplied by population density to give total welfare. Total welfare below the level achieved at the maximum sustainable size (K) is shaded. Despite average welfare always being positive, the welfare-optimal population size (O) is less than the maximum sustainable population size under the “late” (O=0.75) and “continuous” (O=0.81) scenarios. Total welfare continues to increase up to K under the “early” model (O=1.00), where higher population densities have a smaller effect on average welfare.
Figure 2
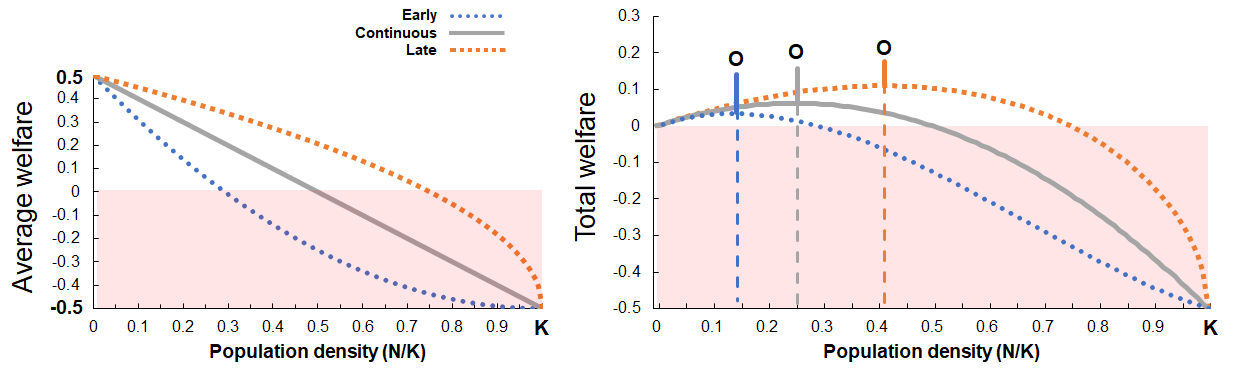
Left: As the population grows from 0 to K average welfare declines from net-positive to net-negative (red shading). A population of wild animals might appear to have very poor welfare at their natural population density, yet have the potential for good welfare at lower population density. Right: In such a case, their total welfare would be maximized by sustaining a medium-sized population, with “Late” density effects increasing the population’s optimal size and potential welfare.
Population density could be managed (and any effects ameliorated) by reducing birth rates, culling individuals from the existing population, or increasing resource availability. Culling is currently the default method for managing animal densities, usually targeting those considered “pests.” Although welfare is occasionally considered, this approach is suboptimal because it involves inflicting suffering on some animals and cutting their lives short (even though culling methods may be less painful than natural causes of death[18]). Non-lethal reduction of population density could be achieved through fertility control, directly limiting the number of animals born without shortening the lives of extant individuals. A complementary approach is reducing the effective density of a population by increasing the quantity or quality of its habitat using the principles of restoration ecology. This could reduce density and improve welfare in the short-term without requiring any reduction in population size. However, without additional measures artificially limiting their growth rate, populations would simply return to their natural sizes and any associated harmful effects of density, so to be sustainable long-term this would still need to be paired with fertility control or another method. A combination of fertility control and habitat improvement could form the basis of a welfare-focused approach to wildlife management. Such an approach must also take into account non-target impacts on other species before being put into practice[19].
Conclusions
It is currently technologically infeasible to make population management decisions that consider the needs of every individual wild animal. We therefore need to determine guiding principles to help us predict the likely results of various population management projects, even under uncertainty about the absolute level of welfare the relevant animals experience. Understanding the density-dependence of welfare in a given population provides one such principle. Furthermore, given sufficient information about absolute welfare levels, this approach could also be used to identify a window of effect sizes where an intervention is expected to increase total welfare relative to the natural long-term size of a population.
The effects of varying levels of density on survival and reproductive rates are exceedingly difficult to determine for any population, given the generational timescales involved and the fact that any population density other than K must by definition be unstable without outside intervention. As a result, precise estimates of density-dependence are rare in the literature, though there is empirical and theoretical support for certain generalizations. Direct evidence on wild animal welfare is also lacking, though we can make inferences from survival rates, body condition and behavior. Research in both of these areas could be high-impact, as an understanding of how welfare expectancy varies with population size would be crucial for planning many large-scale wild animal welfare interventions.
-
World Wildlife Federation. 2018. Living Planet Report - 2018: Aiming Higher. ↩︎
-
Andren, H. (1994). Effects of habitat fragmentation on birds and mammals in landscapes with different proportions of suitable habitat: a review. Oikos, 355-366. ↩︎
-
Ripple, W. J., Wolf, C., Newsome, T. M., Hoffmann, M., Wirsing, A. J., & McCauley, D. J. (2017). Extinction risk is most acute for the world’s largest and smallest vertebrates. Proceedings of the National Academy of Sciences, 114(40), 10678-10683. ↩︎
-
Senar, J. C., Montalvo, T., Pascual, J., & Peracho, V. (2017). Reducing the availability of food to control feral pigeons: changes in population size and composition. Pest management science, 73(2), 313-317. ↩︎
-
Doidge, D. W., Croxall, J. P., & Baker, J. R. (1984). Density‐dependent pup mortality in the Antarctic fur seal Arctocephalus gazellu at South Georgia. Journal of Zoology, 202(3), 449-460. ↩︎
-
Murphy, S. M., Augustine, B. C., Ulrey, W. A., Guthrie, J. M., Scheick, B. K., McCown, J. W., & Cox, J. J. (2017). Consequences of severe habitat fragmentation on density, genetics, and spatial capture-recapture analysis of a small bear population. PloS one, 12(7), e0181849. ↩︎
-
McMahon, C. R., Harcourt, R. G., Burton, H. R., Daniel, O., & Hindell, M. A. (2017). Seal mothers expend more on offspring under favourable conditions and less when resources are limited. Journal of Animal Ecology, 86(2), 359-370. ↩︎
-
Nettle, D., Monaghan, P., Gillespie, R., Brilot, B., Bedford, T., & Bateson, M. (2015). An experimental demonstration that early-life competitive disadvantage accelerates telomere loss. Proceedings of the Royal Society B: Biological Sciences, 282(1798), 20141610. ↩︎
-
Civitello, D. J., Allman, B. E., Morozumi, C., & Rohr, J. R. (2018). Assessing the direct and indirect effects of food provisioning and nutrient enrichment on wildlife infectious disease dynamics. Philosophical Transactions of the Royal Society B: Biological Sciences, 373(1745), 20170101. ↩︎
-
Boulenger, C., Acou, A., Gimenez, O., Charrier, F., Tremblay, J., & Feunteun, E. (2016). Factors determining survival of European eels in two unexploited sub‐populations. Freshwater Biology, 61(6), 947-962. ↩︎
-
Cayuela, H., Schmidt, B. R., Weinbach, A., Besnard, A., & Joly, P. (2019). Multiple density‐dependent processes shape the dynamics of a spatially structured amphibian population. Journal of Animal Ecology, 88(1), 164-177. ↩︎
-
Eberhardt, L. L. (1977). "Optimal" Management Policies for Marine Mammals. Wildlife Society Bulletin, 162-169. ↩︎
-
Gaillard, J. M., Festa-Bianchet, M., & Yoccoz, N. G. (1998). Population dynamics of large herbivores: variable recruitment with constant adult survival. Trends in Ecology & Evolution, 13(2), 58-63. ↩︎
-
Bergman, E. J., Doherty, P. F., White, G. C., & Holland, A. A. (2015). Density dependence in mule deer: a review of evidence. Wildlife Biology, 21(1), 18-30. ↩︎
-
Figler, M. H., Cheverton, H. M., & Blank, G. S. (1999). Shelter competition in juvenile red swamp crayfish (Procambarus clarkii): the influences of sex differences, relative size, and prior residence. Aquaculture, 178(1-2), 63-75. ↩︎
-
Fletcher, W. J. (1988). Intraspecific interactions between adults and juveniles of the subtidal limpet, Patelloida mufria. Oecologia, 75(2), 272-277. ↩︎
-
Briggs, R. A., "Normative Theories of Rational Choice: Expected Utility", The Stanford Encyclopedia of Philosophy (Fall 2019 Edition), Edward N. Zalta (ed.). ↩︎
-
Bradshaw, E. L., & Bateson, P. (2000). Welfare implications of culling red deer (Cervus elaphus). Animal Welfare, 9(1), 3-24. ↩︎
-
Clarke, M., & Ng, Y. K. (2006). Population dynamics and animal welfare: issues raised by the culling of kangaroos in Puckapunyal. Social Choice and Welfare, 27(2), 407-422. ↩︎

This is really amazing, and it'll be interesting to see it applied to wild animal welfare work in the future. I also imagine that there are a lot of applications for farmed animal welfare improvements, etc. Thanks for sharing!
I'm struggling to think of non-human-animal-relevant examples of this, but it seems in principle possible to have welfare effects which depend on total population rather than density. Ideas and technological innovation are (roughly) an example of this in humans. That is, more total humans means more freely shareable ideas/innovations means more welfare. (See e.g. Population growth and technological change: One million BC to 1990.)
Thought I'd just throw it out there in case someone can think of a way to make this relevant to animals.
Good points. If I understand you correctly, these sorts of benefits from population size (independent of the amount of resources/habitat area available) would be essentially the converse of density-independent mortality factors. I've tried to use the term "density" quite broadly here so that effects like these could be accounted for in a single density-dependent welfare curve.
Maybe more standing variation and population resilience which could have indirect effects on welfare over the long-term?