- discounting, and implications for cause prioritization
Introduction
This post works to acknowledge the fact that future people might not exist, within the act of cause prioritization. Doing so entails some form of discounting, with implications for cause prioritization, in particular for neglectedness – a part of the common ITN-framework [1].
Model Setup
I am trained as an economist instead of a philosopher. As such I will not present many words but instead a simple model. Consider the following two variables as primitives:
D(t) – Donation of amount D > 0 at time t
R(t) – Extinction risk in the interval from time 0 to time t
For simplicity, and the sake of argument, consider that:
R(t)/t > 0 is constant
The value of money is constant over time
Result
So we ask ourselves: should we donate now or in the future? Should we donate to a current or a future person?
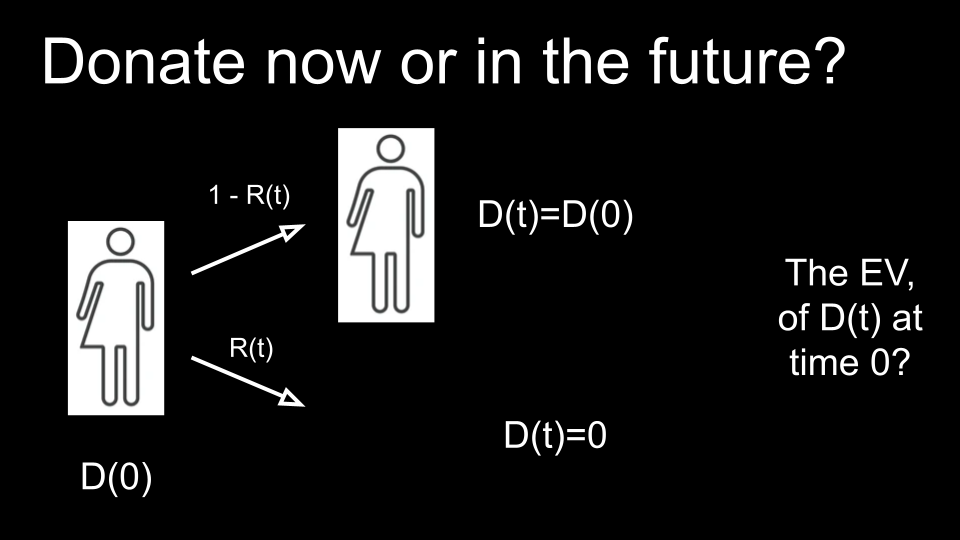
To a current person we can donate D(0) now. This is illustrated at the left side in Illustration 1 below. There you see a current person, now, at time zero. To the right, time t is illustrated. In the future at time t people might still exist, if in the absence of extinction. This occurs with probability 1 - R(t). This hopefully likely scenario is depicted with the top arrow.
With probably R(t), however, extinction does occur, and instead, people no longer exist. When people have gone extinct, the donation D(0) can not find a destination at time t. With the donation non-existent in this scenario, it is effectively zero.
Now what, the illustration finally asks, is the expected value (EV) of D(t), a donation to a future person, at time zero, i.e. now?
We can calculate this with the following mathematics. Applying the definition of an expected value, we sum the probability of each scenario occurring multiplied with its value. We maintain the same order, thus first considering the scenario of non-extinction and then of extinction: (1 - R(t)) * D(0) + R(t) * 0 = (1 - R(t)) * D(0)
The resulting right hand side is smaller than D(0): (1 - R(t)) * D(0) < D(0)
Or without the brackets: D(0) - R(t) * D(0) < D(0)
Thus, if we want to donate D(0) in expected value at time t, i.e. E[D(t)]=D(0), we need to donate D(0) / (1 - R(t)) > D(0) now, into the future. Since, plugging this in for D(0) in the above expected value yields D(0): (1 - R(t)) * D(0) / (1 - R(t)) + R(t) * 0 = D(0)
In conclusion
Future people might not exist. Therefore, to donate D(0) as effectively in future time t to a future person as D(0) now to a current person, we need to add to the donation an additional: D(0) / (1 - R(t)) - D(0)
In other words, to be indifferent between donating some amount D now to a current person and the same amount D at future time point t to a future person, future people need to be positively discriminated by a factor: D(0) / (1 - R(t)).
This (positive discrimination) might thus be advised against, as it is not in line but in conflict with non-discrimination based on time of birth. The first take home message is: To not discriminate between current people and future people we need to care less about future people than about current people, precisely by the risk of their extinction. We could see this as, e.g., analogous to a corrupt government skimming R(t)% off each donation D(t). Or as analogous to the “multiplier effect”, which we know from the difference in cost of living and thereby cost-effectiveness of interventions in ‘developed’ and ‘developing’ countries – terms I object to, since we should all be developing (based on Kate Raworth’s Doughnut model [2], which emphasizes current welfare and possible welfare for future generations).
Discussion
- additional considerations
In reflection we can consider some additional considerations. Distinct from what we assume would not happen – the value of money and/or the extinction rate changing – it might happen that the donation itself is at risk (of going extinct), or becomes obsolete (e.g., future people are very well off and thus have less or no need for it).
In my own schooling, these reasons are also the exact and classical reasons why an economist applies discounting, to consider people further into the future less. The just-mentioned events strengthen the conclusion, but one might also imagine similar events with an opposite effect, and morally we have to judge ourselves what is probable.
Another, final consideration might be that pay it forward effects might differ between people. Different people might have more positive effects than others as a consequence of the donation. Again this might work in either way, but one direction is likely more likely.
- usefulness
And notwithstanding these additional considerations, is the concluded result useful? I believe so. Foremost because it provides a slightly more accurate, and truthful ideal for effective altruism specifically with regards to the moral consideration of future people, thus thereby also slightly reducing an otherwise possible and unwarranted fanaticism.
I think the result we concluded is often already acknowledged but more often not. Messaging would I think be stronger if it was clear, unambiguous, truthful and united in this.
- an implied insight
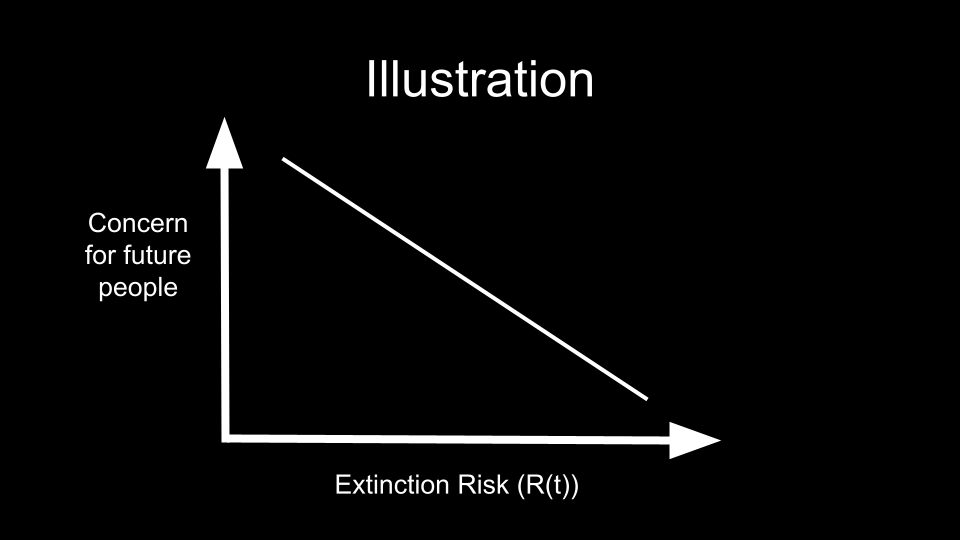
Another insight that results from the concluded result, and that perhaps is also useful, is that as extinction risk decreases we should care more about future (compared to current) people. And also vice versa, as extinction risk increases we should care less about future (compared to current) people. Next Illustration 2 illustrates the inverse relation in this insight.
Extension
In closing, I would like to mention one effect in addition to the inverse relation shown in Illustration 2. This concerns populations of individuals instead of single individuals. And particularly populations aimed at persistence, e.g. by procreating and attempting to survive. Also I will use existential risks now instead of extinction risks, the risk of permanently losing the possibility of a worthwhile future instead of no longer existing, which includes but is more general than only extinction risks.
The additional effect is that as existential risks decrease, the expected value of the whole future increases, and thus the concern for the future one should have and the value of further mitigating existential risks also increases. A positive feedback loop results (which could also take effect in the opposite direction).
Addressing one existential risk, thus increases the value of addressing the next existential risk. And this is also relevant for cause prioritization. (One can also note that with the definition of an existential risk, this positive feedback loop is already logical/intuitive. After all, an existential risk in the future, say at time t, conditions on the absence of an existential risk between time 0, now, and time t: if a worthwhile future has already been permanently lost, it cannot be lost again. Conceptually this also relates to Tarsney’s ENEs [3].)
A second take home message is thus that in prioritizing addressing existential risks, not neglectedness but non-neglectedness might – perhaps counter-intuitively – contribute
Acknowledgements
These thoughts were developed during and with thanks to the 2022 EA Munich Longtermism Fellowship and, before that, the Eon Essay writing contest regarding Ord’s The Precipice.
References
- The ITN framework: https://forum.effectivealtruism.org/topics/itn-framework
- Kate Raworth, Doughnut Economics: https://www.amazon.com/Doughnut-Economics-Seven-21st-Century-Economist/dp/1603586741
- Christian Tarsney, The epistemic challenge to longtermism: https://globalprioritiesinstitute.org/christian-tarsney-the-epistemic-challenge-to-longtermism/
