The Most Important Century Is Not Unlikely

Holden Karnofsky’s “Most Important Century” series of blog posts considers whether we are living at a hinge-moment in the history of the universe. If we are, then the decisions we make will reverberate for the rest of time, impacting nearly all future human lives.

A common initial reaction to this claim is just to ask “What are the chances?”

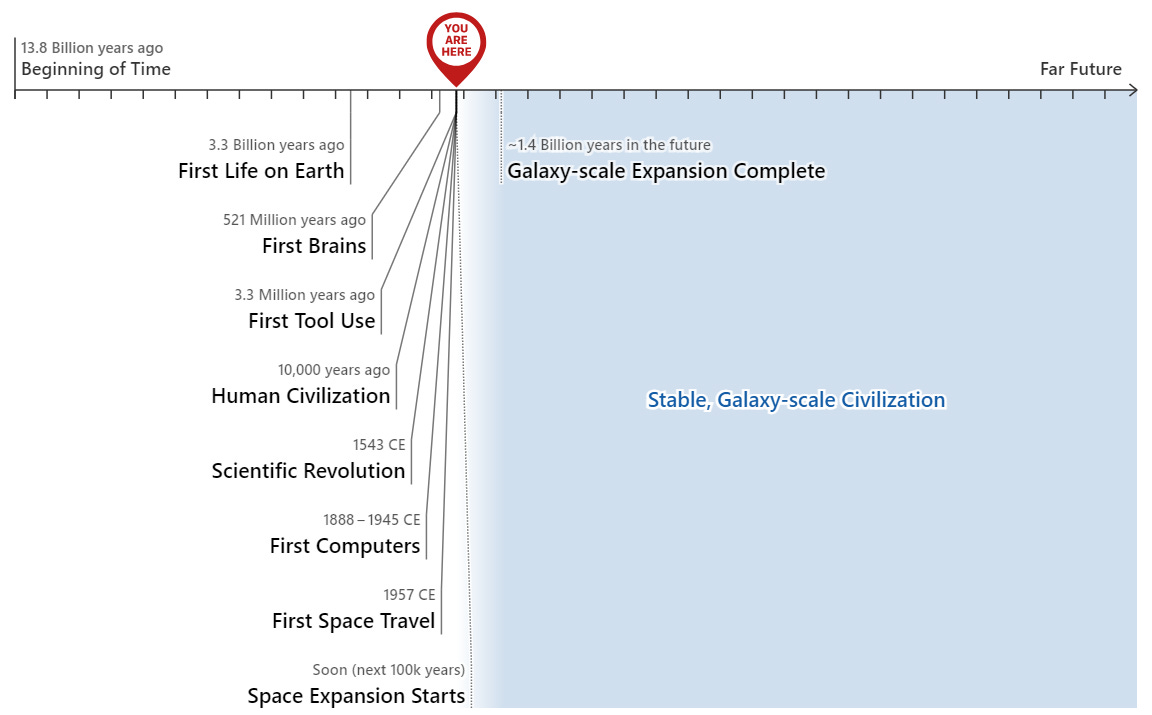
Holden places us in this tiny sliver between the beginning of tool use and the start of a galaxy scale civilization. But if this civilization does arise, then the vast majority of humans who will ever live show up much later on the timeline. If we’re randomly distributed among all humans on the timeline then the average should be billions of years beyond where we find ourselves today. Holden admits that claiming such a low probability event has happened before our eyes is a “wild” claim. But in his blog series Holden lays out the evidence for why we must accept “that our species is simply in a wild situation.” Someone has to exist at the pivotal moments, after all. Looking around it really seems like it might be us, despite the chances.

Pulling from David Deutsch’s discussion of these topics in The Beginning of Infinity, I’ll offer a view on this situation which is “wild” in it’s own way but does not rely on us being in an incredibly unlikely situation.

The Infinity Hotel

The infinity hotel is a mathematical thought experiment originally from David Hilbert. This hotel has a room for every positive integer, and many counterintuitive properties along with it. Deutsch devotes a chapter to expositing some of these properties of infinity using the infinity hotel as a grounding metaphor. For example, the infinity hotel can spend $1000 on every room and make a profit even though each guest only pays $1 to stay there.

Every day, when the management receive all the room rents of one dollar per room, they spend the income as follows. With the dollars they received from the rooms numbered 1 to 1000, they buy complimentary champagne, strawberries, housekeeping services and all the other overheads, just for room 1. With the dollars they received from the rooms numbered 1001 to 2000, they do the same for room 2, and so on. In this way, each room receives several hundred dollars’ worth of goods and services every day, and the management make a profit as well, all from their income of one dollar per room.

Deutsch imagines the hotel collects trash by passing it up the number line at ever increasing, but always finite, speeds until it pops into a singularity. For this reason, guests prefer lower room numbers; fewer bags of trash to pass down. Getting a room number close to the beginning feels like an unlikely prize, but in fact every guest has a room number that is astonishingly close to the beginning. Take any finite number, be it 100, 1000 or 10^36, there are always many more numbers above it than below it. Every room is at the beginning of infinity.

In an infinite set of numbers, there is no such thing as a typical or average number. There are just as many numbers divisible by a trillion as there are odd numbers even though one seems far more common when counting. Similarly, in an infinite future, there is no such thing as a typical or average human. If Holden’s timeline extends forever then no matter where we ended up we’d be head-scratchingly close the beginning of time.

The currently accepted cosmological theory an accelerating expansion of the universe allows for an unbounded number of computations in a universe which is infinite in both space and time.

Can This Go On?

Holden’s claim that humanity is in a wild position is not mainly about our proximity to the beginning of time, although that is a part of it. Rather, it is mostly about our proximity to the beginning of technological progress. Again, whether this is truly an unlikely position to be in or not depends critically on whether the sequence of technological progress is infinite or not. If it is infinite then we’ll always be strangely close to the beginning.

Holden’s case that progress cannot be infinite is mostly based on the fact that continuing acceleration of progress leads to infinite productivity in finite time i.e a singularity. Progress has to top out somewhere before it transcends physical limits.

A distinction should be made here between unbounded and bounded infinities. A sigmoid curve like this one sees infinite progress in the sense that it’s always getting bigger from left to right. But no matter how big it gets, it’s progress will always be less than a finite amount. It’s bounded.

The central thesis of Deutsch’s book is that progress is both unbounded and infinite. However, most of the arguments that Deutsch rebuts in his book correspond best to the “skeptical view” that Holden considers: prophecies of the nearing end of scientific progress or fundamental limits on human understanding. His philosophy of fallibilism convincingly argues that we will never reach a final explanation of the universe. No theory can explain itself so there will be problems to improve on in all future knowledge. And his techno-optimist theories of physics and history demonstrate that there is tons of room to grow in our understanding and control of the universe. But these arguments are true with either unbounded or asymptotic progress.

Holden’s argument is unique in that he believes huge advancements in human understanding and control over the universe are likely, but if growth trends continue they will be exhausted fast. Specifically, growth trends match well to a hyperbolic curve. These curves are asymptotic. They reach an infinite value of Y within a finite section of X. The one which best fits our historical data spits out a singularity within several decades of today. Holden assumes this singularity is impossible so growth must either collapse or slow to a crawl or top out soon. Either way, this century looks strange and important even if an infinite history awaits.

Deutsch does consider this singularity argument in the last chapter of the book (emphasis mine):

In 1993 the mathematician Vernor Vinge wrote an influential essay entitled ‘The Coming Technological Singularity’, in which he estimated that, within about thirty years, predicting the future of technology would become impossible – an event that is now known simply as ‘the Singularity’. Vinge associated the approaching Singularity with the achievement of AI . . . On the other hand, I see no reason to single out AI as a mould-breaking technology: we already have billions of humans.

Most advocates of the Singularity believe that, soon after the AI breakthrough, superhuman minds will be constructed and that then, as Vinge put it, ‘the human era will be over.’ But my discussion of the universality of human minds rules out that possibility. Since humans are already universal explainers and constructors, they can already transcend their parochial origins, so there can be no such thing as a superhuman mind as such. There can only be further automation, allowing the existing kind of human thinking to be carried out faster, and with more working memory, and delegating ‘perspiration’ phases to (non-AI) automata . . . For instance, there will be ever-more-efficient human–computer interfaces, no doubt culminating in add-ons for the brain . . . Artificial scientists, mathematicians and philosophers [will never] wield concepts or arguments that humans are inherently incapable of understanding. Universality implies that, in every important sense, humans and AIs will never be other than equal.

Similarly, the Singularity is often assumed to be a moment of unprecedented upheaval and danger, as the rate of innovation becomes too rapid for humans to cope with. But this is a parochial misconception. During the first few centuries of the Enlightenment, there has been a constant feeling that rapid and accelerating innovation is getting out of hand. But our capacity to cope with, and enjoy, changes in our technology, lifestyle, ethical norms and so on has been increasing too, with the weakening and extinction of some of the anti-rational memes that used to sabotage it. In future, when the rate of innovation will also increase due to the sheer increasing clock rate and throughput of brain add-ons and AI computers, then our capacity to cope with that will increase at the same rate or faster: if everyone were suddenly able to think a million times as fast, no one would feel hurried as a result. Hence I think that the concept of the Singularity as a sort of discontinuity is a mistake. Knowledge will continue to grow exponentially or even faster, and that is astounding enough.

This argument isn’t directly addressed to Holden’s so the clash between them can be confusing. On one hand, Deutsch is saying that AI powered growth won’t feel like a discontinuous singularity in hindsight because we’ll be growing in our knowledge and capacity for growth/change along with it. On the other hand, he is optimistic about creating “universal” AIs and over-clocking human brain speeds a million times, which leaves open the question of what happens when that growth starts to reach physical limits.

Deutsch doesn’t say more about this argument, but I see three possible resolutions which have different implications for Holden’s argument.

One is that growth continues infinitely but slows down significantly like in Dwarkesh Patel’s simmer scenario. But this still leaves us questioning why the growth rates during our time were so aberrantly fast and gives our century, or at least our epoch, a greater than normal importance.

Another is to embrace the singularity. After all, we do infinite things in finite steps all the time. Whenever we move, we cross through an uncountable number of points in the continuity of space-time. We observe singularity’s all around the universe in the form of black holes. The infinity hotel argument that all observers would find themselves strangely close to the beginning would still apply in this case. Emulated brains or duplicators will create an infinite number of observers between any time to the left of the singularity and the singularity. So the number of observers to that came before you will be dwarfed by what comes after no matter where you show up. In this case this century is still the most important, but in the same sense that the 10km between the event horizon and the center of a black hole are the most important distance. Loosely, the amount of ‘experience’ can still be unbounded and infinite within that time as long as it keeps getting faster.

The final possible resolution is that the hyperbolic model of growth is mistaken and we’re able to sustain exponential rates of growth infinitely. Although continuing at an exponential pace indefinitely is hard to imagine, what has already happened so far would have been impossible to imagine a thousand years prior. New knowledge comes with new problems to solve and new areas to grow that we could not predict now by definition. This century would be remarkable in that it lies close to the very beginning of an infinite expansion, but every subsequent century will share this distinction.

Conclusion

Deutsch’s and Holden’s perspective are not completely incompatible. If Deutsch’s position that technological progress is infinite and unbounded is true, then Holden’s predictions of radical technological change in close proximity are confirmed. Even the observation that we seem luckily (or unluckily) close to the beginning of this process is true. But Holden’s argument that this position is very unlikely and important due to its outsized influence on the future doesn’t work in the context of infinite and unbounded progress.

Deutsch positions the book as a case against the much more common beliefs that progress is in some ways impossible or undesirable or almost over.

Holden makes a more sophisticated argument that even if infinite growth is possible in some sense, most future centuries will not see as much influential change as ours did. Hitting a hard-stop end of technological progress seems unlikely. But if tech progress is like some sigmoid curve that’s nearly flat on the edges and vertical in the middle, then even though a maximum level of progress is never reached, a finite period of time contains almost all growth and likely a large influence on the future. It would also mean that progress is bounded, so things improve forever but a finite amount of progress is made. Deutsch doesn’t dive deep on the possible functional forms of technological progress, but he does claim several times that progress is both infinite and unbounded.

I am not sure how Deutsch would respond to Holden’s piece. I can see him dismissing Holden’s doubts that a technological singularity is not possible as a parochial concern and explaining why quantum physics means they are possible. I can also see him coming up with an explanation for why growth will be exponential specifically and not hyperbolic or sigmoidal. Either way, they both see technological change having huge effects on the next century. Although Deutsch’s unbounded optimism contrasts with Karnofsky’s vigilant anxiety, they think that promoting, guiding, and preparing for the coming century of immense change is important.