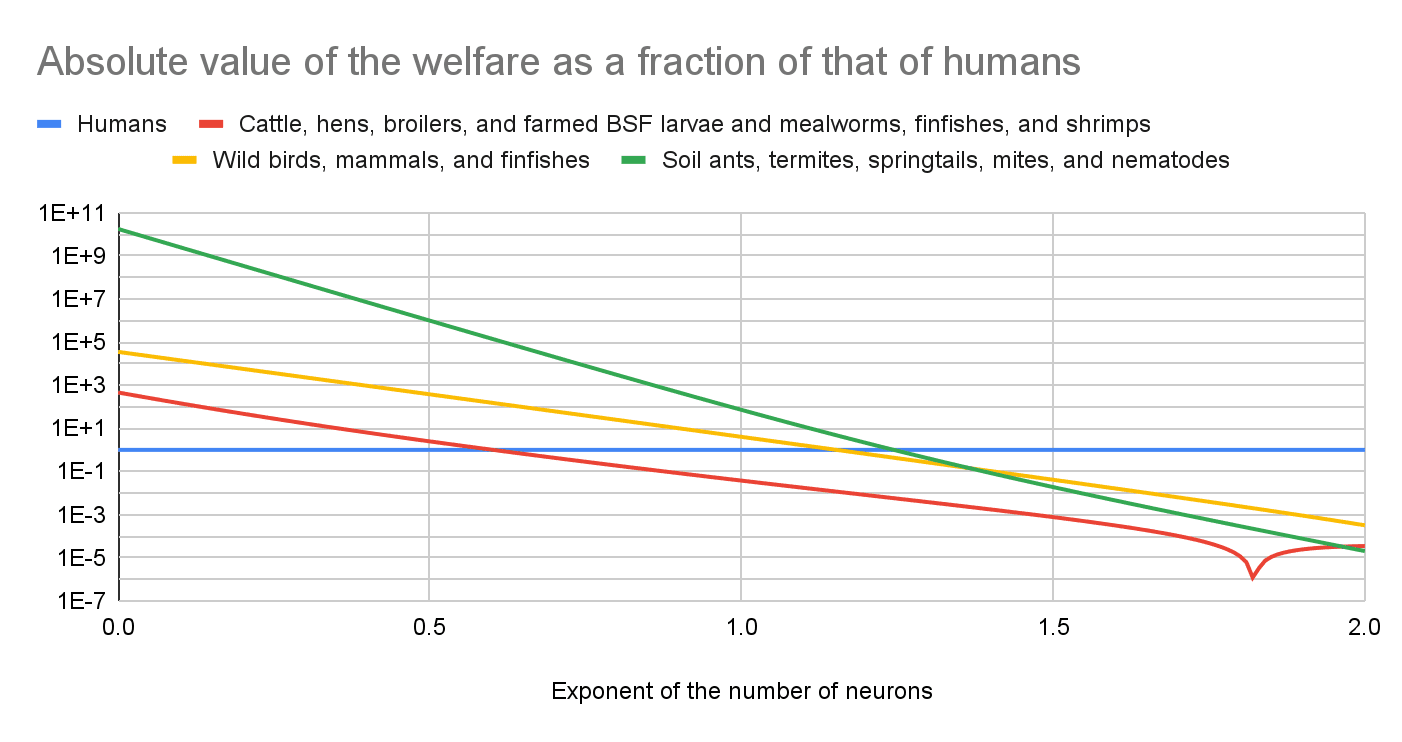
Thanks for the clarifying comment, Jim. I agree with all your points. For individual (expected hedonistic) welfare per fully-healthy-animal-year proportional to "individual number of neurons"^"exponent 1", and "exponent 1" from 0.5 to 1.5, which I believe covers reasonable best guesses, I estimate that the absolute value of the total welfare of:

• Farmed shrimps ranges from 2.82*10^-7 to 0.282 times that of humans.
• Soil nematodes ranges from 0.00252 to 902 k times that of humans.

Moreover, the above ranges underestimate uncertainty due to considering a single type of model for the individual welfare per fully-healthy-animal-year. At the same time, the results for individual welfare per fully-healthy-animal-year proportional to "individual number of neurons"^"exponent 1" can be used to get results for individual welfare per fully-healthy-animal-year proportional to "proxy"^"exponent 2" if "proxy" is proportional to "individual number of neurons"^"exponent 3". All of "exponent 1", "exponent 2", and "exponent 3" can vary. I am using different numbers because they are not supposed to be the same.

And you said things that suggests you agree in this recent interview. You seemed to have deviated from your previous "nematodes obviously dominate" view. Or did I miss something?

I think my previous view was more "it is very difficult for effects on soil animals or ones with a similar number of neurons not to be the major driver of the overall effect in expectation". I would say this was my view in this post. The bullet of the summary starting with the following summarises it well. "I believe effects on soil animals are much larger than those on target beneficiaries". In any case, I was certainly overconfident about the dominance of effects on soil animals or ones with a similar number of neurons.

1. In all the cases you're describing there was a shift from battery cages to enriched cages. So that is two eras of cages potentially in one overall housing unit. 2. I think there is also additional years in advance of a ban to be considered, markets, particularly now on cage-free in Europe have shifted significantly in advance of the bans announced and I think the same thing is happening in countries we will soon see bans from.

Makes sense.

Hi. You tested prior distributions for the probability of consciousness with means ranging from 10 % (= 1/(1 + 9)) for "low" to 90 % (= 9/(1 + 9)) for "high". I feel like this underestimates the uncertainty considering "The choice of a prior is often somewhat arbitrary". Have you considered testing prior distributions with means ranging, for example, from 10^-6 to 99.999 %? Relatedly, how much would the uncertainty increase if you had considered a wider range of possible updates via allowing for stronger levels of support and demandingness, whose corresponding likelohood ratios range from 2 % (= 1/50) to 50 (from Table 2 of the report)? I worry the range of results one gets is overwhelmingly determined by the range of priors and updates. I suspect the final probabilities of consciousness with span many orders of magnitude for priors with means ranging from 10^-6 to 99.999 %, and possible updates with likelihood ratios randing from 10^-6 to 10^6. You focus on updates in the probability of consciousness in light of the evidence, not on the values of the probability of consciousness. However, it might be better to neglect these even more.

Hi Alfredo. I would be curious to know your thoughts on my post All pains are comparable?. You are welcome to comment there.

Summary

• I agree there are pains which feel qualitatively different in the sense of having distinct properties. For example, annoying and excruciating pain as defined by the Welfare Footprint Institute (WFI).
• Some think there are pains whose intensity is incomparably/qualitatively worse than others. For instance, some believe averting an arbitrarily short time of excruciating pain in humans is better than averting an arbitrarily long time of annoying pain in humans. In contrast, I would prefer warming up slightly cold patches of soil for sufficiently many nematodes over averting 1 trillion human-years of extreme torture.
• Consider a human body as described by the state of all of its fundamental particles. Are there any 2 states which are only infinitesimally different whose pain intensities are not quantitatively comparable? I do not see how this could be possible. So I conclude the pain intensities for any 2 states of a human body are quantitatively comparable.

Hi Wladimir.

Point 2: The Risks of Aggregating Intensities and Durations

I would be curious to know your thoughts on my post All pains are comparable?. You are welcome to comment there.

Summary

• I agree there are pains which feel qualitatively different in the sense of having distinct properties. For example, annoying and excruciating pain as defined by the Welfare Footprint Institute (WFI).
• Some think there are pains whose intensity is incomparably/qualitatively worse than others. For instance, some believe averting an arbitrarily short time of excruciating pain in humans is better than averting an arbitrarily long time of annoying pain in humans. In contrast, I would prefer warming up slightly cold patches of soil for sufficiently many nematodes over averting 1 trillion human-years of extreme torture.
• Consider a human body as described by the state of all of its fundamental particles. Are there any 2 states which are only infinitesimally different whose pain intensities are not quantitatively comparable? I do not see how this could be possible. So I conclude the pain intensities for any 2 states of a human body are quantitatively comparable.

Hi Alex. Thanks for the summary and additional points.

Furnished cages typical lifespans are considered to be 15-25 years. 

I agree with this range. This assessment of the economic impact of phasing out furnished cages in Flanders analyses depreciation periods of 20 and 25 years in Figure 7, whose translation to English is below.

This report exploring the consequences of banning enriched cages in the Netherlands (here is an English translation) discusses "a depreciation period of 15 years".

Beyond just the systems, the houses they are built in have lifespans of around 50 years.

I assume this is not a determinant factor. Otherwise, I would have expected economic assessments to consider a longer depreciation period than 15 to 25 years, and transition periods longer than this too. Across 10 bans in Europe, I got a time between the annoucement of the ban until it starts applying to all systems ranging from 4 to 28 years, with the mean being 12.2 years.

@JamesÖz 🔸  points about advocacy cost and public support resonate with me. My understanding is where we have seen furnished/larger cages pop up, like in Europe, Canada, Australia, South Korea briefly in the US. This hasn't been an advocate push. The push has been for cage-free and the industry has lobbied to have that lowered to furnished/larger cages.

I wonder whether some sympathy from animal advocates towards furnished cages relative to conventional cages was needed to get furnished cages. Without that sympathy, in cases where cage-free was not really on the table, the outcome could have been conventional instead furnished cages? If so, animal advocates could still advocate for cage-free, but make it clear that furnished cages are better than conventional cages.

@Mia Fernyhough point about any cage putting a cap on welfare improvement resonates. I see

Did you mean to add something else? The sentence above does not end with a dot.

@Joren Vuylsteke shared a chart of the change and I think by starting from 2009, it misses some of the shift to cage-free which was already happening in advance of that. I can share a chart in DM if anyone would like. ~50M was cage-free in 2003, ~75M in 2006. Countries like Germany leading this.

Eyeballing Figure 3 of this report from Compassion in World Farming (CIWF), the one below which Joren was referring to, there were around 80 M cage-free hens at the start of 2009 in the countries in the EU today, 60 M in barns, and 20 M in free-range. In addition, it looks like there were 220 M in cages, which implies a total of 300 M (= (220 + 80)*10^6), of which 26.7 % (= 80*10^6/(300*10^6)) were cage-free. The EU banned conventional cages 3 years later. It looks like around 10 % of laying hens in China are cage-free. So I wonder whether there are tractable ways of pushing for a ban on conventional cages there, or more states in India.

Overall, one of the strongest things points from my perspective is being aware that there are definitely waves of change in the systems that we can benefit on focussing on.

Agreed.

Hi Michael. That is fair. On the other hand, what readers ignore or not depends on how the results are communicated. It would be harder to ignore uncertainty about AI timelines if AI2027 was e.g. AI2027-2047, and this would still undercommunicate uncertainty. The difference between the 90th and 10th percentile dates of artificial superintelligence (ASI), as defined below, is more than 100 years for Daniel Kokotajlo and Eli Lifland, the 2 main forecasters of the AI Futures Model (which superseded AI2027).

Thanks for the post, Zoe.

Thanks for the very relevant sources you have been sharing too. I strongly upvoted your initial comment because I have found this thread valuable.

The report you linked exploring the consequences of banning enriched cages in the Netherlands (here is an English translation) says conventional cages had fully depreciated in 2012.

Generally speaking, the majority of cage rearing systems were built between 1995 and 1998. 1999. With a depreciation period of 15 years, these systems had an average book value of zero in 2012.

2012 is when the ban on conventional cages in the EU started. So the above supports your take that cages will only be banned when they are near the end of their lifetime. However, I do not think this means a ban on cages in the EU will start, for example, in either 2032 or 2047 (= 2032 + 15). I think it just means the ban will have to be announced 15 years before it enters into force such that the economic loss is minimised. This is in agreement with the report above.

The total financial loss from the inventory of enriched cages, cages to be enriched, and rearing cages is €11.8 million. The loss calculation is based on a ban effective in 2012. If the period of use is shorter or longer, the financial loss will also be proportionally higher or lower. If the ban were to take effect in 2017, the financial loss would be €2.1 million. If the end date were to be postponed to 2020, the financial loss would be €0.7 million. In 2022 [15 years after 2007, when the report was published], the financial loss will be zero because the inventory, after a 15-year depreciation period, will have a residual value of zero.

As a result, if the EU announces a ban on furnished cages in 2026, I guess it will only start applying to all cages (instead of just new cages) in 2041 (= 2026 + 15) or so. Here is an estimate of the economic loss from shortening the transition period. From Table 1.1 of van Horne and Bondt (2023), the housing cost for furnished cages is 3.39 2021-€/hen, 4.84 $/hen (= 3.39*1.22*1.17). For hens with a lifespan of 70 weeks (WFI assumes "60 to 80 weeks for all systems"), 1.34 hen-years (= 70*7/365.25), the housing cost of furnished cages is 3.61 $/hen-year (= 4.84/1.34). I estimate there were 149 M hens in furnished cages in the EU in 2024. So I think renewing all furnished cages in the EU would cost 538 M$ (= 3.61*149*10^6), 1.20 $/citizen (= 538*10^6/(450*10^6)). I speculate 50 % of the value can be recovered via exporting the cages to countries outside the EU. Consequently, for cages fully depreciating in 15 years, the cost of shortening the transition period by 1 year would be 17.9 M$ (= 538*10^6*(1 - 0.50)/15), 0.0398 $/citizen (= 17.9*10^6/(450*10^6)).

As a side note, the calculations for the Netherlands did not account for the possibility of exporting the cages.

Because the systems are permitted in other EU countries, it is possible to sell enriched cages, and to a lesser extent, enriched cages, on the international market. Any potential proceeds from such a sale have not been taken into account in these calculations.

Hi Angelina.

It is also really interesting and encouraging to hear that you think welfare in some cage-free systems is continuing to improve over time.

Relatedly, Schuck-Paim et al. (2021) "conducted a large meta-analysis of laying hen mortality in conventional cages, furnished cages and cage-free aviaries using data from 6040 commercial flocks and 176 million hens from 16 countries". Here is how they describe their findings in the abstract.

We show that except for conventional cages, mortality gradually drops as experience with each system builds up: since 2000, each year of experience with cage-free aviaries was associated with a 0.35–0.65% average drop in cumulative mortality, with no differences in mortality between caged and cage-free systems in more recent years. As management knowledge evolves and genetics are optimized, new producers transitioning to cage-free housing may experience even faster rates of decline. Our results speak against the notion that mortality is inherently higher in cage-free production and illustrate the importance of considering the degree of maturity of production systems in any investigations of farm animal health, behaviour and welfare.