It’s important to estimate the long-term impacts of our actions, but we often can’t observe long-term outcomes within a decision-relevant time frame. David Rhys Bernard, a PhD candidate at the Paris School of Economics, recently tested an alternative approach — measuring the short-term impacts of different interventions on a variety of “surrogate” outcomes, then using those outcomes to reach a long-term impact estimate. In this talk, he explains his findings and their implications.

Below is a transcript of David’s talk, which we’ve lightly edited for clarity. You can also watch it on YouTube and read it on effectivealtruism.org.

The Talk

This talk is about how to estimate the long-term effects of a program. I think there are two main takeaways:

1. How economists, and in particular microeconomists, think about long-term effects and the methods we might use to estimate them. 
2. Whether the method for estimating long-term effects that I’ve researched and generated works well.

So why do we care about long-term impacts? Well, I think they are important in many different domains. Christian [Tarsney] gave an EA Global talk on whether we could predict the impact of our actions now on the far future of humanity in thousands or millions of years. Clearly, these super-long-term impacts are important. 

However, I think our focus shouldn't solely be on super-long-term impacts, but on short long-term impacts, [to use a] slightly awkward [turn of phrase]. There are a few reasons why we should focus on these. First, I don't think we know yet whether we can predict long-term outcomes — not even in the range of five, 10, or 20 years. So it seems pretty clear to me that we want to make sure that we can do this for a 10-year period before we think about doing it for a 100-year period. 

Second, these short long-term impacts are important in and of themselves. GiveWell recommends [donating to] deworming [charities] mostly on the basis of one randomized controlled trial [RCT], which found that deworming during childhood had persistent impacts on outcomes like adult income and food consumption 15 years after the deworming. This randomized controlled trial was run, in part, by one of [the 2019] Nobel Prize winners, Michael Kremer. It's a really excellent RCT on a really important topic. It’s producing a lot of policy-relevant information. 

The problem with these long-term randomized controlled trials is that they're super difficult to do. You have to follow thousands of people over dozens of years. You have to have a lot of patience, a lot of planning, and a lot of foresight. So the question is: Given that we don't want to wait 20 years — and don't want to go to all of this effort to estimate long-term effects — how can we do it? How can we estimate long-term effects without having to wait a long time? 

This problem is one that people working in medicine face quite a lot as well. Medics often want to know what the impact of some new treatment or drug is on a long-term outcome such as life expectancy. So how do medics approach this?

 

They break it down into three steps. Let's say we're trying to estimate the impact of a new surgery to cut out a cancerous tumor on a long-term outcome like life expectancy:

1. The first step medics would take would be to look at the effect of the treatment on a short-term outcome or “surrogate outcome,” to be more technical. So in our case, we'd look at the effect of the surgery on tumor size.
2. The second step would be to look at the relationship between our short-term outcome and our long-term outcome. So we’d look at the relationship between tumor size and mortality rates. 
3. Once we have these two pieces of information, we can [take the third step]. We can combine the information on the effect of the surgery on tumor size with the relationship between tumor size and mortality rates to [estimate] the effect of the surgery on life expectancy.

This method works well in medicine because there's often only one mechanism — one channel — through which the short-term treatment affects the long-term outcome. In other words, the treatment only affects the long-term outcome of life expectancy through tumor size. In social science, this assumption is much less credible. There are many different mechanisms through which any given treatment can affect long-term outcomes. So how can we deal with this? 

A recent economic theory paper by some other economists — who will probably win the Nobel Prize in the future — has generalized this method to work with many different short-term outcomes. 

 

So how does this method work? We need two data sets. The first one is from an experiment and the second one is an observational data set. In this experiment [shown on the slide above] we have a randomly assigned treatment (T). So let's say this treatment is cash transfers.

We also have baseline characteristics. These are characteristics of the recipients of the cash transfer that are fixed at the time treatment is randomized. They could be things like the education of recipients’ parents, or their age.

And finally, we have the short-term outcomes of the experiment. These would be outcomes like whether a recipient is enrolled in school or what their test scores are. 

In the observational data set, we don't have a randomized treatment. That's why it's observational. So this data set could include things like censuses or household surveys. We need the same baseline characteristics and the same short-term outcomes that we have in the experimental data. Additionally, we need information on the long-term outcomes that we care about. So let's say this is whether recipients have enrolled in tertiary education — whether they go to university. If we have this long-term outcome and the experimental data, there'll be no problem, right? We could just take the average of the long-term outcome in the treatment group and subtract the average long-term outcome in the control group. This would give us the impact of the treatment because of the random assignment. 

We almost can think of this as a missing data problem. We don't have a Y or long-term outcome in the experiment. So how can we get it? There are three steps to this method:

 

1. Take the observational data and estimate a predictive model from it. With this model, we predict the long-term outcome as a function of the short-term outcomes and the baseline characteristics. Our model tells us what the relationship between the long-term and the short-term is. We can use a simple method like linear regression for this, or we can use fancy machine learning methods, whichever you prefer.
2. Fit this predictive model to the observational data. We can then use ĥ sub-0 to predict Y in the experiment. We feed the information on the short-term outcomes to the baseline characteristics in the experiment, and this produces predictions of the long-term outcome in the experiment. 
3. Treat the predictions of the long-term outcome as if they're the actual long-term outcome. We can take the average predicted long-term outcome in the treatment group, and the average predicted long-term outcome in the control group, and the difference between the two is the predicted impact of the program — even though we don't have actual information on the long-term outcome. 

So this is the surrogate-index method. The original paper also introduces another method, the surrogate-score method, which is slightly less intuitive. I don't have time to go through it, but it requires exactly the same data and exactly the same assumptions.

 

So what are the assumptions we need to make for this to work? 

The first assumption is the main one: surrogacy. [The assumption here is that] treatment is independent of the long-term outcome. It’s conditional on the short-term outcomes and the baseline characteristics. This is slightly confusing and almost meaningless, but luckily we can represent it in a graph, which is hopefully more clear. 

 

[The idea is that] the treatment has an impact on the short-term outcomes, [represented on the slide by] S. The short-term outcomes have an impact on the long-term outcome, and the baseline characteristics have an impact on both the short-term outcomes and the long-term outcome. But there's no relationship between the treatment and the baseline characteristics, because the treatment is randomized. Therefore, the surrogacy assumption requires two things. First, it requires that the treatment has no direct impact on the long-term outcome. There's no arrow going from T to Y. What this means is that the entire effect of the treatment on the long-term outcome must flow through the short-term outcomes. These short-term outcomes mediate the full impact of the treatment on the long-term outcome.

 

The second [requirement] of [the surrogate] assumption is that there are no unobserved baseline characteristics that affect both the short-term outcomes and the long-term outcome. There are no U variables. Any of these characteristics which affect both outcomes must be observed; they must be in this X. 

So this is a pretty demanding assumption. We need all of these channels through which the treatment affects the long-term outcome, and we need all of these potential “confounders” between the short-term outcomes and the long-term outcome. The assumption becomes more credible the more data we have. The more short-term outcomes we have, the more mechanisms we can account for between treatment and the long-term outcome, and the more baseline characteristics we have, the less likely it is for there to be an unobserved [characteristic] that affects both the short-term and the long-term outcome. 

The second assumption is the compatibility-of-samples assumption. This means that the distribution of the long-term outcome (conditional on the short-term outcome) and the baseline characteristics is the same in both the experimental and the observational data. 

Why do we need this assumption? Remember that we use observational data to estimate a predictive model for estimating the relationship between the long-term outcome and the short-term outcomes. If the relationship between the long-term outcomes and short-term outcomes is different in the experiment and the observational data, then obviously the model won't produce good predictions of the long-term outcome in the experimental data. 

If these two assumptions are satisfied, along with a few other minor technical ones, then the surrogacy approach should work; we should be able to predict long-term estimates of treatment. So the question, then, is: Do these assumptions hold up in real-world data? 

[For my research,] I take long-term randomized controlled trials from development economics, where I can exploit the fact that I have information on the treatment, the short-term outcomes, and the long-term outcome. And I compare the true long-term outcome from the RCT with an implementation of my surrogacy method.

 

The data I use is from a 2019 paper by Barrera Osorio and various coauthors. They’re studying conditional cash transfers in Colombia. They have two randomized controlled trials. One takes place in San Cristóbal, where they have two treatments. Students are randomly assigned to either the “basic” treatment or the “savings” treatment. Those in the basic group get $30 every two months, conditional on being enrolled in school. The savings-treatment students only get $20 every two months, but they also get $50 at the start of every academic year as a way to encourage them to buy school uniforms and supplies to help ensure that they return to school. 

In Suba, in the second randomized controlled trial, the treatment is also $20 every two months. But instead of $50 at the start of every academic year, it's $300, conditional on enrolling in tertiary education — a strong monetary incentive for students to continue their education.

The original paper studies the effects on the short- and long-term outcomes. The short-term outcomes they study include things like enrollment, whether the students have graduated from secondary school, and whether they've enrolled in tertiary education in 2012 (eight years after the start of the program). The long-term outcomes are observed 12 years after the start of the program, in 2016, and these include information on whether students have enrolled in tertiary education, whether they’ve enrolled on time, and whether they’ve graduated from tertiary education.

The headline results of this original paper are that the basic and the savings programs have zero long-term effect, while the incentive program has a positive long-term effect. This is the data I use. But how do I use it to test my surrogacy method?

 

Let's take Suba as our experimental data. Because we have the treatment, the baseline characteristics, the short-term outcome, and the long-term outcome, we can estimate the impact of the treatment on the long-term outcome. We simply take the average of the long-term outcome in the treatment group and the average of the long-term outcome in the control group. And this yields an unbiased estimate of the long-term effect of the treatment. We can think of this as the “true effect” that we're wondering if the surrogacy method can replicate.

Now let's implement the surrogacy method. Let's pretend that we don't have long-term data. We don't have the Y in the experiment. We just have the treatment, baseline characteristics, and short-term outcomes. This now mimics the experimental data set — the short-run experiment that we need for the surrogacy method. 

Now we can turn to San Cristóbal and pretend that we don't have information on treatment status. We just have baseline characteristics, short-term outcomes, and the long-term outcome. It now mimics the observational data that we need for the approach. So we've created these two sort of fake data sets, which we can use to implement the surrogacy approach. We take our observational data from San Cristóbal and we estimate a model to predict the long-term outcome as a function of the short-term outcomes and the baseline characteristics. Once we have this model, we fit it to our experimental data to produce predictions of our long-term outcome.

Then, with these predictions, we compare the average predicted long-term outcome in the treatment group with the average predicted long-term outcome in the control group. This produces a separate surrogacy estimate. So are these results similar to the RCT results? 

 

Along the top [of the above slide] are the three different treatments. So for the incentive treatment on the far right, I'm taking Suba as the experimental data and San Cristóbal as the observational data. (I can, of course, do the reverse and take San Cristóbal as my experimental data.) 

Along the bottom are three different outcomes: enrolled, enrolled on time, and graduated. So the red dots are the true estimates from the RCT — the ones we're trying to replicate. And the bar around them is in the 95% confidence interval. The green dots are from the surrogate index method that we explained earlier. And the blue dots are from the surrogate score method that we had to skip over. 

So what do we see? I think the most notable thing is that the blue and the green dots are always within the 95% confidence interval of the RCT. This means they're never statistically significantly different from the RCT estimate. This is good news for us. Even better, these dots are not only in the confidence interval, but often close to the center of it. So the actual estimates from these surrogacy methods are very similar to the actual estimates from the RCT. 

I was pretty happy when I got this news. This method seems to work really well and it has potentially a lot of use cases for predicting long-term impacts.

However, it's always good to test the robustness of your methods. How well do they work when we're not implementing them in ideal circumstances? That's what I do next.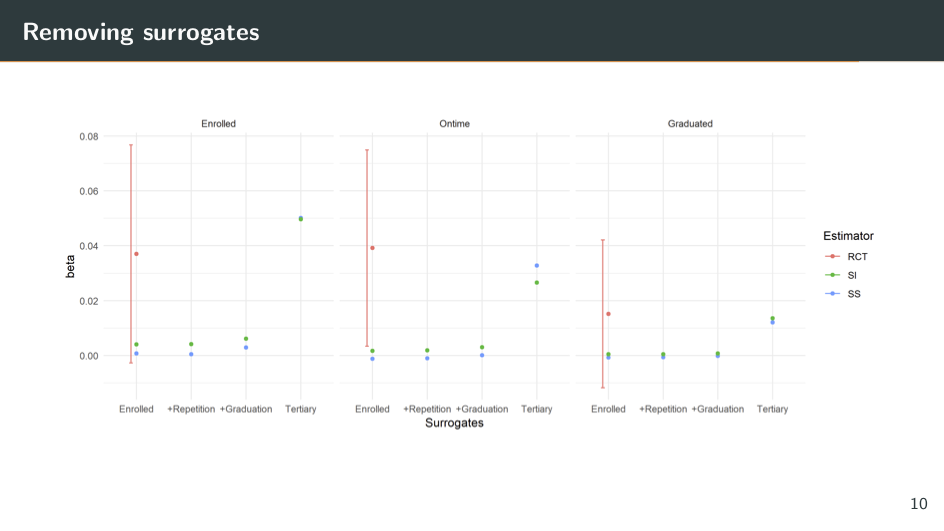 

 

Here I'm re-implementing the surrogacy method, but I'm only using a subset of the short-term outcomes to predict the long-term outcome. I'm not using the full set of them. So along the top [of the slide] are the three different outcomes: enrolled, enrolled on time, and graduated. And along the bottom, now I have different subsets of the short-term outcomes of the surrogates.

In the far left column, in each graph there’s just information on enrollment in secondary school from 2006 to 2008. Here, the surrogacy methods produce estimates pretty close to zero, which is also very far away from the RCT estimates. What this suggests is that these enrollment variables are not good surrogates. They're not mediating the impact of the treatment on the long-term outcome and they're not predictive of our long-term outcome, so they're not helping us estimate a long-term effect.

Next, I keep the enrollment variables. I also add information on where the students have repeated grades (whether they've been held back) or whether they've dropped out of secondary school. Their performance is almost identical again; this method is not helping us predict the long-term impact. 

Next, I took information on whether students have graduated from secondary school. If we squint really hard, I think we can see a slight improvement in the methods, but we're still very far away from the actual RCT estimate. 

Finally, I [ignore] all of these variables and just take information on whether students have enrolled in tertiary education in 2012. Now the method seems to be doing much better. The point estimates are much closer to the RCT estimate.

 

So what does this mean? It means that the variables on whether recipients enrolled in tertiary education by 2012 are the ones doing all of the work. These are the variables that are mediating the long-term impacts, the ones that are predictive of the long-term outcome. 

To some degree, this is really unsurprising. Of course tertiary enrollment in 2012 is going to be predictive of things like tertiary enrollment in 2016 or tertiary graduation. So I think this highlights that the surrogacy method can work, but it's very sensitive to having these key surrogates that are predictive of the long-term outcome. 

To summarize, I've tested a new method to estimate long-term effects, and the headline conclusion is that it works well on a time frame of four to five years, but once we go longer — 10 years or so — and we have fewer of these short-term outcomes, we're really struggling with this method. It doesn't work so well.

I think the broader takeaway is that estimating long-term impacts is really, really hard. Here we have an RCT, and trying to predict impacts over only 10 years is still a struggle. I think this means we should be pretty skeptical of strong claims that we can predict the impact of our actions now in 50 or 100 years, or even more.

However, this is just an economics perspective. I think it's highly likely that other disciplines have much better methods for estimating long-term effects. So I'm very interested in learning about those. I'm doing work on testing this method in different contexts, because currently I just know how it performs in one context. Maybe it performs better in others. 

I'm also trying to improve the method to work in longer time frames using fancier machine learning [methods]. But again, I'm very interested in hearing more from people who want to estimate long-term impacts — people in climate science and forecasting literature often have useful insights. So if you're interested in this topic, please send me an email at david.rhys.bernard@gmail.com. Thank you very much.

Discussant: Thank you very much, David. I'm going to give a summary of what I think Dave's contributions are. I think this is a big and important question. So, as David said at the beginning, there's a deficit of evidence on long-term effects. I think this paper helps address key changes related to EA causes.

First, [it helps address] global poverty, where the application is quite clear, and other short-termist causes like animal welfare, where there's just a lack of evidence on the longer-term effects of interventions (I'm talking about five or more years). And in these cases, whether these effects that we see in the short term in an RCT are persistent might dominate the accuracy of the short-run effect.

Here are some examples:

* If you dig into GiveWell’s cost-effectiveness analysis, quite often one of the really important factors is how long they think these effects are going to last. Are they going to last five years or 20 years? That can play a big role in the strength of evidence behind an intervention. 
* Blattman et al. look at a cash transfer program in Uganda and find that after nine years the treatment group converges with the control group.
* Two other papers by Banerjee et al., and Bandiera et al. actually find good evidence of long-run persistent effects of programs targeting the ultra-poor. These are programs which combine cash transfers or a productive asset with some training and some other intervention. 

Basically, the evidence on persistence of effects is normally quite small. We have a few examples where it turns out to be really important, but generally it's quite hard to [estimate], as David concluded. And [his approach] seems like a potentially useful method to improve the accuracy of our estimates over the long run.

The second area is to do with long-termism, where it's essentially very hard to predict long-run effects over timescales of 20, 50, 100, or maybe 1,000 or more years. And I think Dave makes a pretty good case that we need to make some progress on this, and that within the field of economics, we're pretty terrible at it. I pulled a quote from David's paper: “It's probable that if we're not able to first predict the impact of our actions in 10 years’ time, we'll also be unable to predict their effect in 100 years’ time.”

I think that's pretty compelling. And then David also uses the term “marginal long-termism,” arguing that one way of doing better on long-termism is to push people on the margin to think about longer-term effects. I think this work can help contribute to that. And what David does in his papers is basically [apply] a recently developed technique by future Nobel Prize winners: Athey, Imbens, Raj Chetty, and Kang. Look out for them. If you do want to place your bets [on future Nobel Prize winners], as David suggested, they are a pretty good bet. 

They've developed this technique, but as far as I know, this is the first empirical application and test of this multiple-surrogates approach. They put a paper out there in 2016, but there haven't been many applications. I think it's great that David has taken it and applied some real-world data. And this might improve our estimates of long-term effects of interventions which have short-run evaluations. David's results are encouraging and might help us make incremental progress toward understanding very long-run effects. 

In terms of next steps, which David and I have discussed, I think the next thing he might want to do is understand the variance of these estimates better. He showed you point estimates of this application and where they land relative to the long-run RCT. He has another application where he runs some bootstrap simulations, which tells us something about the variance of the performance of the estimator. And I think a key thing will be to look at additional applications — especially those with larger true effects.

In the paper that David shared, two of the three interventions have close to zero or statistically insignificant effects. My worry is that it's not a very high bar to clear, because if there's a close to zero effect on the intermediate and long-run outcomes, then you're obviously going to estimate a zero effect on the long-run outcomes when you see the intermediate ones. I think David has some ideas for [addressing] this, so maybe we'll talk about that a little bit. 

Another issue is understanding the relative performance of the two surrogate techniques. David mentioned that there are two different ways to do that, and it's not clear from a theoretical perspective which one will perform better. I think that's something to explore. 

I'm going to pose a few questions and then let you respond, David. The first one: Is there a theoretical reason to expect the bias to be toward zero? And if that is the case, might this be a very useful lower-bound estimate for long-run effects in cases where we don't know the true effects?

The second question or comment is: Do we have an understanding of when we might expect this method to perform well? So you started to address this in your last few slides, where you showed that different combinations of the intermediate outcomes perform in a variety of ways. And if we don't know the true effect, would you be confident in saying, “This data set seems to have the correct surrogates”? My sense is that this is quite hard to know, and it will be more of an art — not a science — when trying to understand when this method might perform well.

I have some suggestions that maybe we can discuss afterwards: 

* Can you develop an informal test of this if you have multiple rounds of surrogates, and then project that into the future? 
* Similarly, can you develop decision rules as to which estimates to use and how to implement the estimator? So for example, which variables do we need to include as a surrogate? Or which variables do we need to include as a control? 
* I'd be interested to hear your thoughts on the bias toward zero. Do you have a sense of when we expect this to perform well and how we might implement this? 

And remember to submit audience questions on the Whova app, because I will switch to those. Over to you, Dave.

David: Okay. I’ll start at the beginning, with theoretical reasons to expect a bias toward zero. I think your point is exactly right — that if there's no intermediate effect, then obviously we're going to predict no long-term effects. This is almost mechanical. 

However, in cases where there is an intermediate effect, I don't think there's any plausible reason why we should expect there to be a long-term effect estimate of zero. This is for the surrogate-index method. For the surrogate-score method, instead of predicting the long-term outcome with the observational data, essentially you do predictions of whether someone is treated in the experimental data, The structure of this estimator means that if your predictions are biased towards 0.5 (i.e., random), then that estimator is pushed toward zero.

So that's a potential concern. But I don't think there's any reason to expect your predictions of treatment probability to be biased towards 0.5. If there is noise, then it should be going both ways, up and down, not necessarily toward —

Discussant: So we can't use that to bound our estimates in any predictable way?

David: I don’t think so, no. I need to do more theoretical work on this as well.

The next question was “When will we expect the method to perform well?” I think the obvious thing is that the method works well over shorter time frames. In that case, the prediction problem is harder and you have more data to make a prediction. 

I also think it might work better with simpler interventions — for example, cash transfers, where effects seem to be persistent and slowly fade out. As long as there's some sort of consistent pattern, I expect it to work better. 

A counter-example to this would be deworming, where we have pretty large short-term effects, no medium-term effects, and then large long-term effects. Again, it's this really confusing pattern that we don't understand, and I think this method would not perform particularly well there.

But as I said, it also works better the more short-term outcomes and baseline characteristics we have. 

That leads to the next issue. I would like to do a further test with the deworming data. I'm waiting for it to come online; I've been promised many times it will be online soon. We're not quite there yet. But if you can nag someone, that'd be helpful.

Discussant: I'd be interested to hear a bit more about the other applications that you have in mind. What papers are already available that you could apply this to? And what would be the perfect hypothetical application for testing this method — what would that experiment look like?

David: So the other things I have in mind are deworming and a few other conditional cash transfer papers. The main problem is that these RCTs only started to be run 20 years ago in development economics. So these long-run follow-ups are happening right about now. People are trying to publish the long-term results themselves; currently, they're not willing to share the data, because they have to get their publications out. However, there are a few cash transfer papers, like that Blattman paper you mentioned, where there's potential. I’m looking into those.

From a theoretical perspective, it might be nice to stick with cash transfers to make the analysis simpler and reach stronger conclusions at least for cash transfers, even if they're not strong for other things. But I would like to explore this across many different data sets. 

[What was] your second question again?

Discussant: It was about the hypothetical best experimental method that you could test this method with.

David: Ideally, that would [involve] many waves of short-term data — from two, four, six, eight, 10 years after treatment. That would allow me to explore the effect [and answer questions like] Can I use the two-year outcomes to predict the four- or six-year outcomes? So the deworming data looks a little bit like that. I think they're on four or five rounds of data collection now. I’m just waiting for that.

Discussant: If anyone has an RCT with four or five rounds of data collection, please get in touch with David. I think we're out of time. Thank you very much.