Risk neutrality is the idea that a 50% chance of $2 is equally valuable as a 100% chance of $1. This is a highly unusual preference, but it sometimes makes sense:
Exampleville is infested with an always-fatal parasite. All 1,024 residents have the worm.
For each gold coin you pay, a pharmacist will deworm one randomly selected resident.
You only have one gold coin, but the pharmacist offers you a bet. Flip a weighted coin, which comes up heads 51% of the time. If heads, you double your money. If tails, you lose it all.
You can play as many times as you like.
It makes sense to be risk neutral here. If you keep playing until you've saved everyone or go broke, each resident gets a 0.51^10 = 1 in 840 chance of survival. If you don't play, it's 1 in 1,024.
For a few of the most scalable interventions, I think EA is like this. OpenPhil seems to expect a very low rate of diminishing returns for GiveWell's top charities. I wouldn't recommend a double-or-nothing on GiveWell's annual budget at a 51% win rate, but I would at 60%.[1]
Most interventions aren't like this. The second $100M of AI safety research buys much less than the first $100M. Diminishing returns seem really steep.
SBF and Caroline Ellison had much more aggressive ideas. More below on that.
Intro to the Kelly Criterion
Suppose you're offered a 60% double-or-nothing bet. How much should you wager? In 1956, John Kelly, a researcher at Bell Labs, proposed a general solution. Instead of maximizing Expected Value, he maximized the geometric rate of return. Over a very large number of rounds, this is given by
Where is the proportion of your bankroll wagered each round, and is the probability of winning each double-or-nothing bet.
Maximizing with respect to gives
Therefore, if you have a 60% chance of winning, bet 20% of your bankroll on each round. At a 51% chance of winning, bet 2%.
This betting method, the Kelly Criterion, has been highly successful in real life. The MIT Blackjack Team bet this way, among many others.
Implicit assumption in the Kelly Criterion
The Kelly Criterion sneaks in the assumption that you want to maximize the geometric rate of return.
This is normally a good assumption. Maximizing the geometric rate of return makes your bankroll approach infinity as quickly as possible!
But there are plenty of cases there the geometric rate of return is a terrible proxy for your underlying preferences. In the Parasite example above, your bets have a negative geometric rate of return, but they're still a good decision.
Most people also have a preference for reducing the risk of losing much of their starting capital. Betting a fraction of the Kelly Bet gives a slightly lower rate of return but a massively lower risk of ruin.
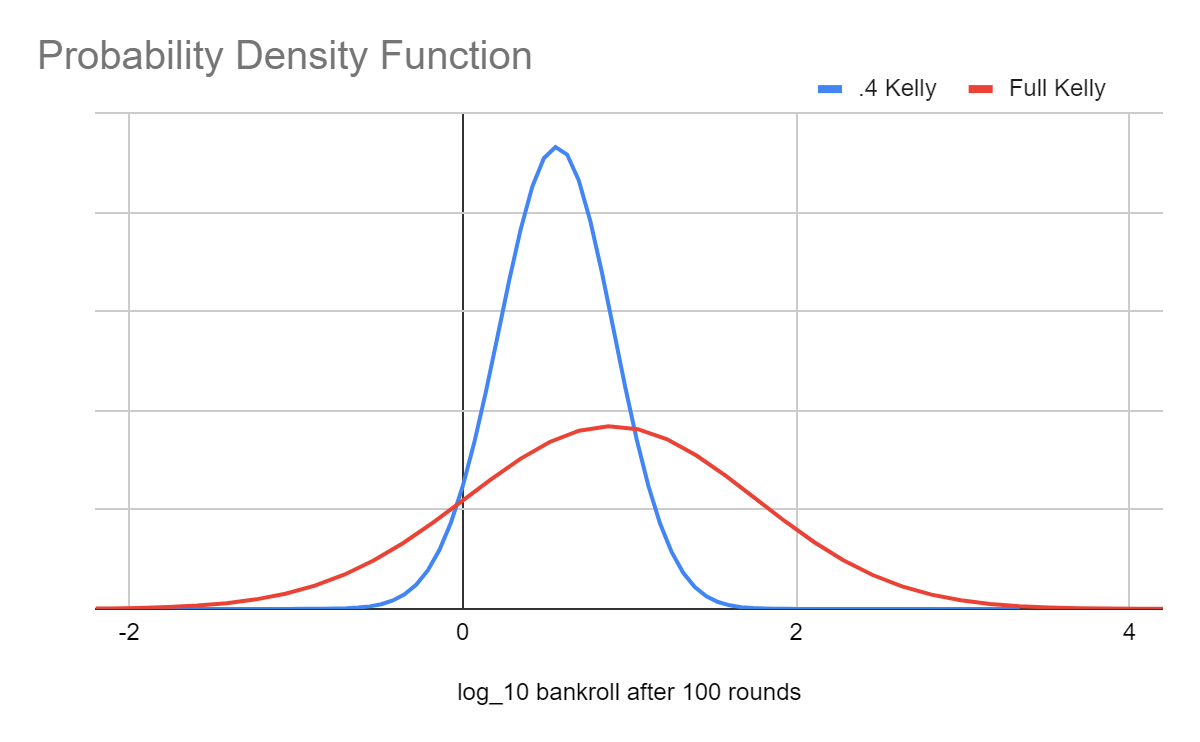
Above: distribution of outcomes after 100 rounds with a 60% chance of winning each bet. The red line (Full Kelly) wagers 20% of the bankroll on each round, while the blue (.4 Kelly) wagers 8%. The x-axis uses a log scale: "2" means multiplying your money a hundredfold, while "-1" means losing 90% of your money.
Crucially, neither of these distributions is better. The red gets higher returns, but the blue has a much more favorable risk profile. Practically, 0.2 to 0.5 Kelly seems to satisfy most peoples' real-world preferences.
Treat risk preferences like any other preference
SBF and Caroline Ellison both endorsed full Martingale strategies. Caroline says:
Most people don’t do this, because their utility is more like a function of their log wealth or something and they really don’t want to lose all of their money. Of course those people are lame and not EAs; this blog endorses double-or-nothing coin flips and high leverage.
She doesn't specify that it's a weighted coin, but I assume she meant a positive EV bet.
Meanwhile, SBF literally endorses this strategy for the entire Earth in an interview with Tyler Cowen
[TYLER] ... 51 percent, you double the Earth out somewhere else; 49 percent, it all disappears. Would you play that game? And would you keep on playing that, double or nothing?
SBF agrees to play the game repeatedly, with the caveats that the new Earths are created in noninteracting universes, that we have perfect confidence that the new Earths are in fact created, and that the game is played a finite number of times.
I strongly disagree with SBF. But it's a sincerely held preference, not a mistake about the underlying physical reality. If the game is played for 10 rounds, the choices are
A. One Earth, as it exists today
B. 839/840 chance that Earth is destroyed and a 1/840 chance of 1,024 Earths
I strongly prefer A, and SBF seems to genuinely prefer B
One of my objections to B is that I don't believe a life created entirely makes up for a life destroyed, and I don't believe that two Earths, even in noninteracting universes, is fully twice as valuable as one. I also think population ethics is very unsolved, so I'd err toward caution.
That's a weak objection though. Tyler could keep making the odds more favorable until he's overcome each of these issues. Here's Tyler's scenario on hard mode:
50%, you create a million Earths in noninteracting universes. 50 percent, it all disappears. Would you play that game? For how many rounds? Each round multiplies the set of Earths a millionfold.
I still wouldn't play. My next objection is that it's terrible for SBF to make this decision for everyone, when I'm confident almost the entire world would disagree. He's imposing his preferences on the rest of the world, and it'll probably kill them. That sounds like the definition of evil.
That's still a weak objection. It doesn't work in the least convenient world, because Tyler could reframe the scenario again:
50%, you create a million Earths in noninteracting universes. 50 percent, it all disappears. In a planetwide election, 60% of people agreed to play. You are a senior official with veto power. If you don't exercise your veto, then Earth will take the risk.
I won't answer this one. I'm out of objections. I hope I'd do the right thing, but I'm not sure what that is.
Did these ideas affect the FTX crash?
I think so. I predict with 30% confidence that, by end of 2027, a public report on the FTX collapse by a US Government agency will identify SBF or Caroline Ellison's attitude towards risk as a necessary cause of the FTX crash and will specifically cite their writings on double-or-nothing bets.
By "necessary cause" I mean that, if SBF and Caroline did not have these beliefs, then the crash would not have occurred. For my prediction, it's sufficient for the report to imply this causality. It doesn't have to be stated directly.
I have about 80% confidence in the underlying reality (risk attitude was a necessary cause of the crash), but that's not a verifiable prediction.
Of course, it's not the only necessary cause. The fraudulent loans to Alameda are certainly another one!
Conclusions
A fractional Kelly Bet gets excellent results for the vast majority of risk preferences. I endorse using 0.2 to 0.5 Kelly to calibrate personal risk-taking in your life.
I don't endorse risk neutrality for the very largest EA orgs/donors. I think this cashes out as a factual disagreement with SBF. I'm probably just estimating larger diminishing returns than he is.
For everyone else, I literally endorse wagering 100% of your funds to be donated on a bet that, after accounting for tax implications, amounts to a 51% double-or-nothing. Obviously, not in situations with big negative externalities.
I disagree strongly with SBF's answer to Tyler Cowen's Earth doubling problem, but I don't know what to do once the easy escapes are closed off. I'm curious if someone does.
Cross-posted to LessWrong
- ^
Risk neutral preferences didn't really affect the decision here. We would've gotten to the same decision (yes on 60%, no on 51%) using the Kelly Criterion on the total assets promised to EA

In Exampleville (parasite example), if money is infinitely divisible, Kelly betting will save everyone with probability 1.
If bets must be an integral number of coins (and you start with only one coin, a very inconvenient world!), the strategy of "bet the highest amount not more than Kelly, except always bet at least one coin and never bet more than necessary to reach 1024", will save everyone with probability of approximately 0.038, or about 1 in 26, which is significantly better than 1 in 840.
In an intermediate scenario where gold coins are divisible into 100 smaller units for betting purposes, the probability for an analogous strategy will exceed 0.94.
While these strategies do involve betting higher than Kelly in the sole situation that you bet your last betting unit instead of giving up, in general it is fair to call them Kelly variants in contrast to "always bet everything".
The reason that Kelly variants are vastly superior to always betting everything is that the terms of your hypothetical are that "You can play as many times as you like." It is difficult to conceive of why anyone would risk more than Kelly with this allowance (again with exceptions for your last betting unit).
You can salvage the example by saying that you are limited to 10 bets.
However, if you are limited to, for example, 20 bets, then the best strategy will be some intermediate that is riskier than Kelly but definitely less risky than "always bet everything".
My advice to readers is that betting more than Kelly is usually a terrible idea and if you think it's a good idea, you're probably making a mistake. The fact that a thought experiment, in an intelligently written article, went awry and gave an example where risk neutral betting is worse than Kelly variants when it was supposed to do the opposite, is a great example of the danger.
Nonetheless, I concede that for small and medium donors, betting 100% of your funds-to-be-donated on a 51% coin flip is fine if it is genuinely limited to your personal donation. However, the reason for this concession is not that I endorse risk-neutral betting for EA, but rather that the correct way to look at the bet in this scenario, when the funds are already "to be donated", is not as part of your personal bankroll, but rather as part of the bankroll of the cause for which you intend to donate them. Since any individual small or medium donor will in all likelihood represent less than 0.1% of the bankroll of the cause, such an individual betting such funds in isolation is in practice never exceeding Kelly betting.
I would still caution against 51% coin flips in a scenario where a large fraction of the EA community coordinates, spreads news of "an opportunity", etc., such that a large fraction of EA funds are risked on highly correlated 51% coin flips, for reasons which are hopefully quite obvious.
I read the example as one in which the pharmacist's only offer is for a series of double-or-lose-all wagers. That is unlikely to be a real-world scenario, admittedly.
Maybe a more realistic hypo would allow betting in tenths of a coin, but after each round, some small fraction of the population is killed by the parasite. Very conservative risk management always looks good if you have a practically infinite time to flip coins before you need to act.
I had the same reading, but then the thought experiment doesn't do anything to justify why double or nothing is better than Kelly betting. It's just better than... not doing anything, I guess, which isn't an impressive conclusion.
I think it's moderately effective as a simplified model that quickly demonstrates the premise in the title could be true in some scenarios.
The basic Kelly bet hypo, as I understand it, also contains some assumptions that are uncommon in the real world (indefinite number of available rounds that result instantly). It's a closer match to many real-world scenarios, but I'd be open to an argument that there are practical scenarios are closer to OP's simplified model than the basic Kelly model. That's what I would be interested in hearing more from OP about.
Thanks, it didn't occur to me that "double your money" in the example meant "double your entire bankroll" not "double some amount that you selected to bet". I think you're right that that's what the author meant, but I share Karthik's concern that you're then comparing "bet everything" to "do nothing".
I understand your concerns about the number of coin flips required. I loosely addressed it in my original comment, noting that even with a fixed limit of 20 bets in Exampleville (but with the ability to select bet size), the optimal approach will be clearly be less risky than "always bet everything".
Furthermore, it's important to consider that any scenario based on a limited number of bets is only applicable to the real world if the bets in the scenario will be the only positive-EV bets you can make in your entire life, or if the resource you are betting will never have any utility outside of the constrained scenario, or something very strange like that. In the real world, if you encounter a positive-EV bet denominated in USD that you are only able to make a limited number of times, even if you have a salient group of people to aid with the outcome of the bet, you need to consider that you may have other positive-EV bets in your life and you may be able to use the USD to help other people in the future if you manage risk more normally and don't blow your entire net worth on the first set of positive-EV bets that you encounter.
With respect, it is highly unusual to call full Kelly betting "very conservative risk management". Most people familiar with the concept consider full Kelly betting to be extremely aggressive.
I definitely wouldn't call full Kelly "very conservative." My point was that in Exampleville and other scenarios with a capped best outcome, a very conservative strategy (e.g., 0.001 Kelly) is trivially superior to even merely conservative strategies if there is practically infinite time to flip coins before you need to act, and flipping coins is a costless activity. So the specification of the constraints is what makes the problem interesting (and realistic). The example shows that there are constraints where very agressive betting makes sense; the rest of the post needs to demonstrate how those scenarios -- or at least somewhat similar scenarios -- might occur in real life.
Bets don't have to be in USD or anything else that is a store of value. One could imagine that the "currency" was virologists in a rapidly-moving pandemic. You can put them on safe research that will save a modest number of lives or tell them to roll the dice on speculative research with a possible big payoff. You can't really "store" their labor for a possible better bet that may appear ten years down the road, or use it for something else very effectively.