On the other extreme, we could imagine repeatedly flipping a coin with only heads on it, or a coin with only tails on it, but we don't know which, but we think it's probably the one only with heads. Of course, this goes too far, since only one coin flip outcome is enough to find out what coin we were flipping. Instead, we could imagine two coins, one with only heads (or extremely biased towards heads), and the other a fair coin, and we lose if we get tails. The more heads we get, the more confident we should be that we have the heads-only coin.
To translate this into risks, we don't know what kind of world we live in and how vulnerable it is to a given risk, and the probability that the world is vulnerable to the given risk at all an upper bound for the probability of catastrophe. As you suggest, the more time goes on without catastrophe, the more confident we should be that we aren't so vulnerable.
what’s the procedure for going the other way -- for extracting an implied annual risk based on a risk over a long timeframe (and an assumed credence)? i guess you’d model it in a pretty similar way.
this probably implies that many of the risk estimates we see in the wild are too high, right? i mean, there’s no way to really know, but i wouldn’t be surprised if many estimates on longer timeframes are actually projections of estimates on shorter timeframes, since the latter may be more manageable to reason about.
If you think there's an exchangeable model underlying someone else's long-run prediction, I'm not sure of a good way to try to figure it out. Off the top of my head, you could do something like this:
def model(a,b,conc_expert,expert_forecast): # forecasted distribution over annual probability of nuclear war prior_rate = numpyro.sample('rate',dist.Beta(a,b)) with numpyro.plate('w',1000): war = numpyro.sample('war',dist.Bernoulli(prior_rate),infer={'enumerate':'parallel'}) anywars = (war.reshape(10,100).sum(1)>1).mean() expert_prediction = numpyro.sample('expert',dist.Beta(conc_expert*anywars,conc_expert*(1-anywars)),obs=expert_forecast)
This is saying that the expert is giving you a noisy estimate of the 100 year rate of war occurrence, and then treating their estimate as an observation. I don't really know how to think about how much noise to attribute to their estimate, and I wonder if there's a better way to incorporate it. The noise level is given by the parameter conc_expert, see here for an explanation of the "concentration" parameter in the beta distribution.
I don't know! I think in general if it's an estimate for (say) 100 year risk with <= 100 years of data (or evidence that is equivalently good), then you should at least be wary of this pitfall. If there's >>100 years of data and it's a 100 year risk forecast, then the binomial calculation is pretty good.
I think it's worth emphasizing more general consequences from switching to this more accurate model, including for other risks. I think one important one is that the expected lifetime of Earth-originating civilizations is longer. Possibly much longer, right?
Do you know of work on this off the top of your head? I know if Ord has his estimate of 6% extinction in the next 100 years, but I don't know of attempts to extrapolate this or other estimates.
I think for long timescales, we wouldn't want to use an exchangeable model, because the "underlying risk" isn't stationary
I'm not sure I've seen any models where the discrepancy would have been large. I think most models with discount rates I've seen in EA use fixed constant yearly discount rates like "coin flips" (and sometimes not applied like probabilities at all, just actual multipliers on value, which can be misleading if marginal returns to additional resources are decreasing), although may do sensitivity analysis to the discount rate with very low minimum discount rates, so the bounds could still be valid. Some examples:
But I guess if we're being really humble, shouldn't we assign some positive probability to our descendants lasting forever (no heat death, etc., and no just as good or better other civilization taking our place in our light cone if we go extinct), so the expected future is effectively infinite in duration? I don't think most models allow for this. (There are also other potential infinities, like from acausal influence in a spatially unbounded universe and the many worlds interpretation of quantum mechanics, so duration might not be the most important one.)
Sorry, I wouldn't have the time, since it's outside my focus at work, animal welfare, and I already have some other things I want to work on outside of my job.
I know if Ord has his estimate of 6% extinction in the next 100 years, but I don't know of attempts to extrapolate this or other estimates.
This doesn't change the substance of your point, but Ord estimates a one-in-six chance of an existential catastrophe this century.
Concerning extrapolation of this particular estimate, I think it's much clearer here that this would be incorrect, since the bulk of the risk in Toby's breakdown comes from AI, which is a step risk rather than a state risk.
Subtitle: Exchangeable models are a better way to extrapolate forecasts
This is a cross-post from my new blog, that I started because of the blog prize.
This post has a companion notebook, check it out here, or clone the repo here.
Probability theory gives us some good tools for reasoning with uncertain knowledge. Probability does not solve every problem we have in this regard, but usually the relevant alternative is some ad-hoc approach using natural language. Many people, including myself, are excited about replacing ad-hoc approaches with more principled approaches based on the probability theory. Probabilities used to represent uncertain knowledge are called subjective probabilities or credences.
By analogy: a ruler doesn’t solve every length measuring problem, but we can still benefit a lot from replacing eyeball guessing with the use of a ruler.
However, if we want to use probability theory to reason with uncertain knowledge, we need to use it correctly. One error that I’ve seen a number of times is when people want to extrapolate credences. Say we have an expert opinion credence in nuclear war occurring in the next 12 months, and we’re interested in knowing the credence in nuclear war occurring in the next 100 years. One way to do this extrapolation is to assume that credences are just like coin flip probabilities. For example, the graph in this tweet makes this assumption:
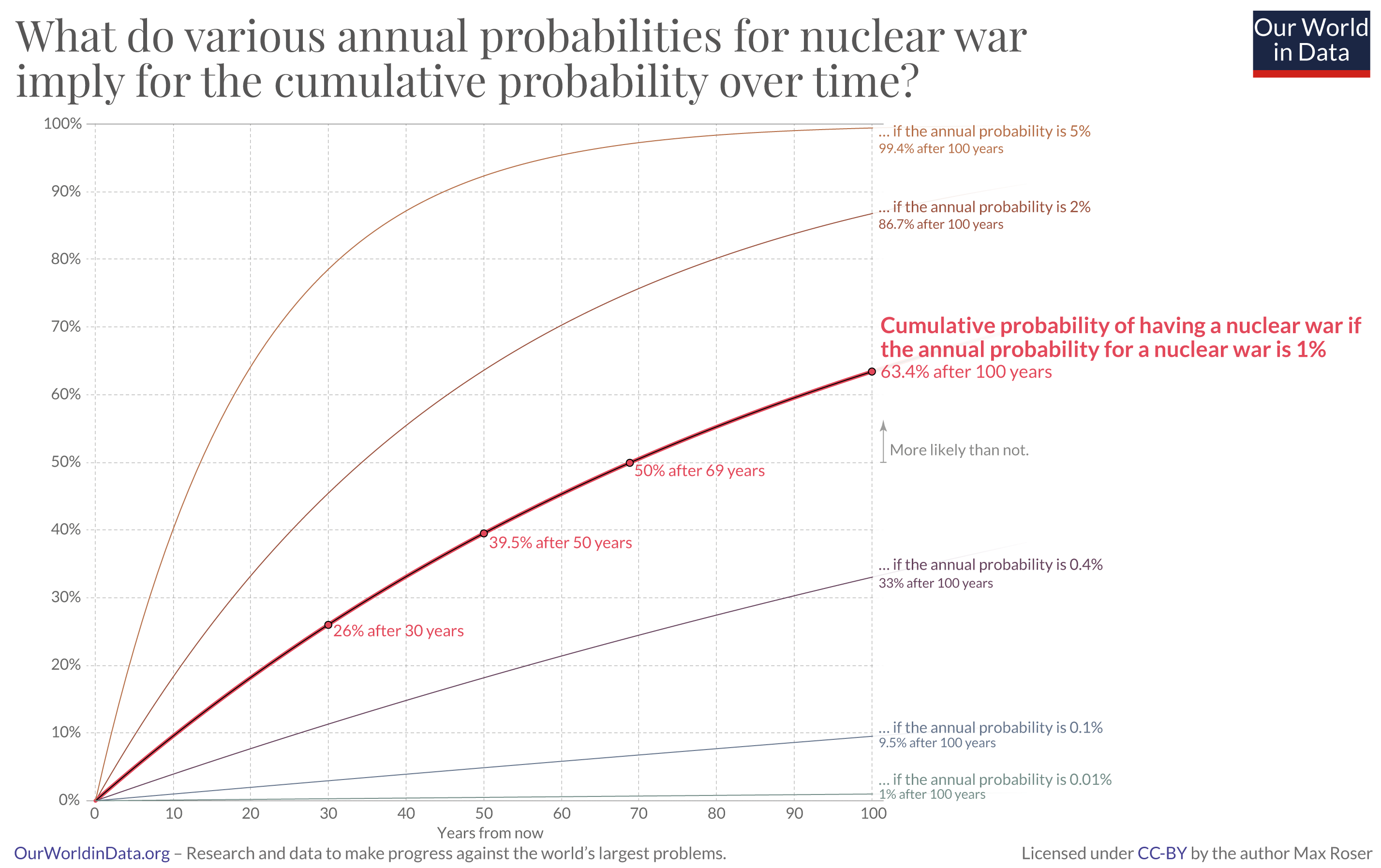
The tweet refers to this article, which notes how expert credences regarding nuclear (around 1%) war in the next year seem to imply fairly high credences in nuclear war in the next 100 year (over 50%).
Both the tweet and in the article assumes that “the probability of a nuclear war in 1 year” behaves like the “the probability of getting heads when you hypothetically flip a fair coin” in order to extrapolate from a 1 year credence to a 100 year credence. However, this is not a reasonable assumption. A hypothetical fair coin uses an independent and identically distributed (IID) probability model, and IID models are inappropriate for a modelling the probability of nuclear war over time given a credence of nuclear war this year.
What’s wrong with IID models?
If I am reasoning with uncertain knowledge, I expect my current state of knowledge to be revised as I learn more. For example, I might right now assign a credence of 1% per year to nuclear war, but if no war happens in the next 50 years I might reduce this credence
An IID model expresses with absolute certainty the long run limiting frequency, with no room for revision at all. I can say the long run relative frequency of heads I’ll get from hypothetically flipping my fair coin is 50%, and I won’t change my view at all even if I get 1 million heads in the first million flips
Our original aim was to reason with uncertain knowledge in a principled way. Never ever changing your views no matter what data you see is an unreasonable way to reason under uncertainty, and IID models are therefore unreasonable models for uncertain knowledge.
To see the difference, compare an IID model that assigns a 5% chance to nuclear war every year to models that starts out assigning a 5% credence to nuclear war, but update this view if years go by with no nuclear war:
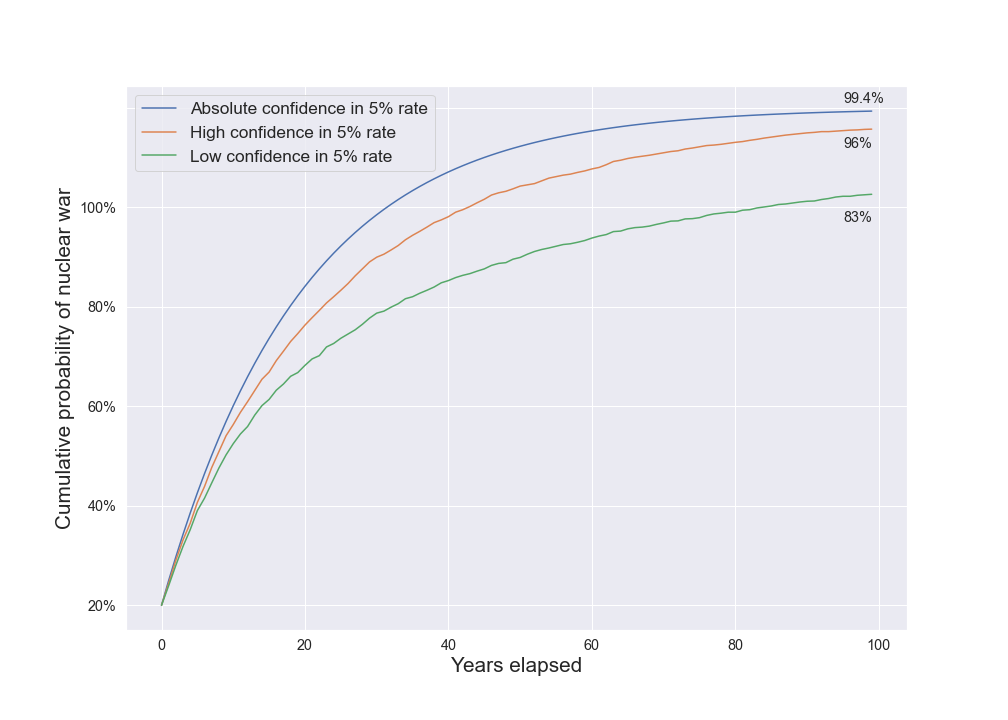
The IID model with this parameter regards nuclear war a near certainty after 100 years, giving only a 0.6% chance to avoiding it. The lower confidence model gives a comparatively much larger 17% chance of avoiding nuclear war in the next 100 years. The difference is because the lower confidence model, on seeing 40 years with no nuclear war, revises its annual credence of war downward while the IID model continues to assume the chance is 5%, whatever it sees along the way. 5% is a very high estimate, and it was chosen to highlight the differences.
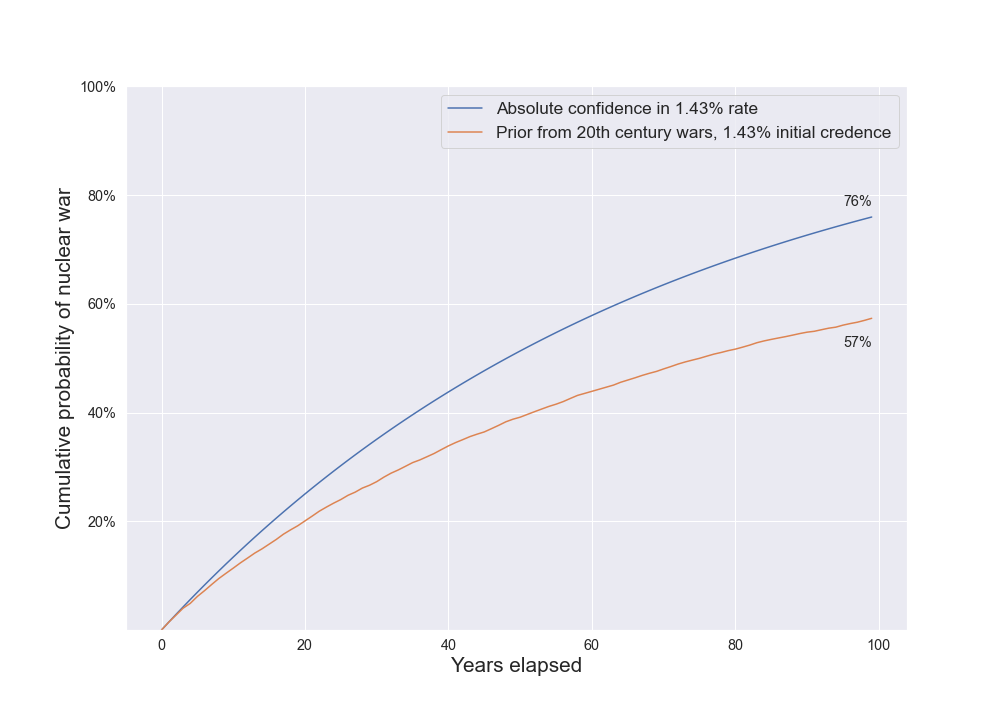
If I try to use more realistic inputs, an IID model give a 76% credence in nuclear war in the next 100 years, while a model with lower confidence in the rate gives a 57% credence.
Exchangeable models
We should not model credences in annual rates as IID. One way to improve is to use exchangeable models instead of IID models. This is what I did to produce the graphs above. We may wish to use a more complicated model again. Exchangeable models are a good first step, as they will allow us to learn from additional data with the minimal additional complexity.
I used numpyro to implement my model, but there are many great alternatives including stan and pymc3. Using numpyro is a bit of an overkill for this problem, but with a probabilistic programming language it is easy to make things a little bit more complicated, whereas with simpler methods we would quickly get stuck.
Conclusion
Forecasts of rates - whether they are annual, weekly or millennial - should not be treated as if they are parameters of an IID probability model. Instead, it is much better to treat them as expectations of exchangeable models; have a look at my notebook for some help getting started in doing this. If you run into trouble, some great resources are cross validated, as well as the project developers for numpyro, stan or pymc3. I would also love to hear if you are trying to implement a probability model and run into trouble.
This is a crosspost from the new Animal Welfare Alignment Newsletter by Anima International. You can subscribe on Substack if you are interested in following these efforts. Audio reading also available on Substack.
The goals of this post are to:
1. Raise a question I see as crucially important to the goal of aligning AI to animal welfare...
Hello! I'm Justin Portela. I got hired by GWWC to make YouTube videos after AI in Context did such a kickass job.
My channel is using that same cinematic, high-production value beauty to talk about everything in the EA universe that isn't AI.
...
This is a linkpost for Request for Proposals: Research and Applied Work on Digital Minds.
I'm glad to announce a request for proposals for research and applied work on digital minds at Longview Ph...
This is an important point. Thanks for sharing.
On the other extreme, we could imagine repeatedly flipping a coin with only heads on it, or a coin with only tails on it, but we don't know which, but we think it's probably the one only with heads. Of course, this goes too far, since only one coin flip outcome is enough to find out what coin we were flipping. Instead, we could imagine two coins, one with only heads (or extremely biased towards heads), and the other a fair coin, and we lose if we get tails. The more heads we get, the more confident we should be that we have the heads-only coin.
To translate this into risks, we don't know what kind of world we live in and how vulnerable it is to a given risk, and the probability that the world is vulnerable to the given risk at all an upper bound for the probability of catastrophe. As you suggest, the more time goes on without catastrophe, the more confident we should be that we aren't so vulnerable.
Nice explanation, thanks