[Crossposting from https://blog.jessriedel.com/2020/09/15/quantum-computing-timelines/ ]
IN SHORT: We attempt to forecast when quantum computers will be able to crack the common cryptographic scheme RSA2048, and develop a model that predicts less than 5% confidence that this capability will be reached before 2039. You can read the full article at https://arxiv.org/abs/2009.05045
Advanced quantum computing comes with some new applications as well as a few risks, most notably threatening the foundations of modern online security.
In light of the recent experimental crossing of the "quantum supremacy" milestone, it is of great interest to estimate when devices capable of attacking typical encrypted communication will be constructed, and whether the development of communication protocols that are secure against quantum computers is progressing at an adequate pace.
Beyond its intrinsic interest, quantum computing is also fertile ground for quantified forecasting. Exercises on forecasting technological progress have generally been sparse — with some notable exceptions — but it is of great importance: technological progress dictates a large part of human progress.
To date, most systematic predictions about development timelines for quantum computing have been based on expert surveys, in part because quantitative data about realistic architectures has been limited to a small number of idiosyncratic prototypes. However, in the last few years the number of device has been rapidly increasing and it is now possible to squint through the fog of research and make some tentative extrapolations. We emphasize that our quantitative model should be considered to at most augment, not replace, expert predictions. Indeed, as we discuss in our preprint, this early data is noisy, and we necessarily must make strong assumptions to say anything concrete.
Our first step was to compile an imperfect dataset of quantum computing devices developed so far, spanning 2003-2020. This dataset is freely available, and we encourage others to build on it in the future as the data continues to roll in.
To quantify progress, we developed our own index - the generalized logical qubit - that combines two important metrics of performance for quantum computers: the number of physical qubits and the error rate for two-qubit gates. Roughly speaking, the generalized logical qubit is the number of noiseless qubits that could be simulated with quantum error correction using a given number of physical qubits with a given gate error. Importantly, the metric can be extended to fractional values, allowing us to consider contemporary systems that are unable to simulate even a single qubit noiselessly.
To forecast historical progress into the future, we focus on superconducting-qubit devices. We make our key assumption of exponential progress on the two main metrics and use statistical bootstrapping to build confidence intervals around when our index metric will cross the frontier where it will be able to threaten the popular cryptographic protocol RSA 2048.
Note that since we are modelling progress on each metric separately we are ignoring the interplay between the two metrics. But a simple statistical check shows that the metrics are likely negatively correlated within each system - that is, quantum computer designers face a trade off between increasing the number of qubits and the gate quality. Ignoring this coupling between the metrics results in an optimistic model.
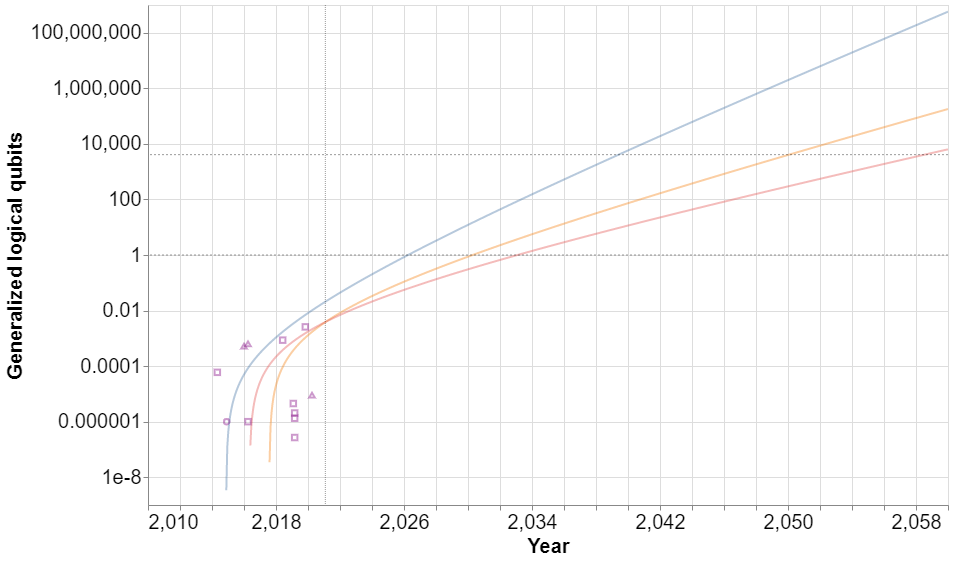
Our main result: the 5%, median and 95% confidence extrapolation for the generalized logical qubit metric using a bootstrapping procedure. The 4100 threshold is where we estimate quantum computing will be able to solve the popular cryptographic scheme RSA-2048. Past recorded values of the metric are shown as purple icons on the graph.
As a point of comparison, last year Piani and Mosca surveyed quantum computing experts and found that 22.7% think it is likely or highly likely that quantum computers will be able to crack RSA-2048 keys by 2030, and 50% think that is likely or highly likely that we will be able to crack RSA-2048 keys by 2035.
Will this be enough time to deploy adequate countermeasures? I discuss this in depth in this other article about quantum cryptanalysis. Given the current rate of progress on the standardization of quantum-resistant cryptography there seems to be little reason for concern (though it should be considered that the yearly base rate for discontinuous breakthroughs for any given technology is about 0.1%).

A plausible timeline of development and deployment of a quantum-resistant cryptography standard, for illustrative purposes. Also shown a summary of expert prediction on attack capabilities. As comparison, our statistical prediction assigns <5% confidence to having quantum computing hardware capable of breaking RSA 2048 before 2039. This figure originally appeared on Assessing the impact of quantum cryptanalysis. The figure is based on an interview with the leader of NIST's Cryptographic Technology Group Lily Chen and educated guesswork.
If you are interested in better understanding our model and assumptions, I encourage you to check out our preprint on the arXiv.

5% probability by 2039 seems way too confident that it will take a long time: is this intended to be a calibrated estimate, or does the number have a different meaning?
Jaime gave a great thorough explanation. My catch-phrase version: This is not a holistic Bayesian prediction. The confidence intervals come from bootstrapping (re-sampling) a fixed dataset, not summing over all possible future trajectories for reality.
It is not intended to be a calibrated estimated, though we were hoping that it could help others make calibrated estimations.
The ways that a calibrated estimate would differ include:
1. The result is a confidence interval, not a credence interval (most places in the paper where it says probability is should say confidence, I apologize for the oversight), so your choice of prior can make a big difference to the associated credence interval.
2. The model is assuming that no discontinuous progress will happen, but we do not know whether this will hold. (Grace, 2020) estimates a yearly rate of discontinous breakthroughs on any given technology of 0.1%, so I'd naively expect a 1-(1-0.1%)^20 = 2% chance that there is such a discontinuous breakthrough for quantum computing in the next 20 years.
3. The model makes optimistic assumptions of progress - namely that a) the rate of exponential progress will hold for both the physical qubit count and the gate error rate, b) there is no correlation between the metrics in a system (which we show it is probably an optimistic assumption, since it is easier to optimize only one of the metrics than both) and c) we ignore the issue of qubit connectivity due to lack of data and modelling difficulty.
If I was pressed to put a credence bound on it, I'd assign about 95% chance that EITHER the model is basically correct OR that the timelines are slower than expected (most likely if the exponential trend of progress on gate error rate does not hold in the next 20 years), for an upper bound on the probability that we will have RSA 2048 quantum attacks by 2040 of <5% + 95% 5% ~= 10%.
Either case, I think that the model should make us puzzle over the expert timelines, and inquire whether they are taking into account any extra information or being too optimistic.
EDIT: I made an artihmetic mistake, now corrected (thanks to Eric Martin for pointing it out)
Do you have a link for (Grace, 2020) ?
The citation is a link: (Grace, 2020)
Just in case: https://aiimpacts.org/discontinuous-progress-in-history-an-update/
It appears to be the extrapolation using exponential growth from current capacity using maximum likelihood to fit the growth rate. Whether you believe the date comes down to how well you think their generalized logical Qubit measures what they're trying to capture.
I think it's worth remembering that asking experts for timelines requiring more than 10 years often results in guessing 10 years, so I would tend to favor a data-based extrapolation over that.