This is interesting, but it feels like the difference needs a little more grounding. After all, "continuity" is always just an approximation - we are not literally building a continuum of AIs, one for each point along the curve. Progress from GPT-2 to GPT-3 or DALL-E to DALL-E 2 is clearly discrete. It seems like the difference is in how discrete it is, which is more of a quantitative difference than a qualitative difference.
The problem is that sometimes you can see a process is actually continuous only ex post. I think I saw this argument in Yudkowski's writing that sometimes you just don't know what variable to observe, so then a discontinuous event surprises you and only after that you realize you should have been observing X, which would make it seem continuous.
Im not up on the literature , but it seems that continuity of technical progress is not a meaningful discussion. Events can be seen as discontinuous or not depending on time scale, information availability, and technical expertise. To me, continuity is a way of operationalizing the question "will we be surprised by AI competence?". If our alignment techniques are always sufficient, then the point is moot regardless of how fast AI improves.
Ps. an interesting possibility is "Lipshitz Continuity", which means that the derivative is bounded. ie. "What's the fastest rate that technology can progress?"
This post will try to explain what I mean by continuity assumptions (and discontinuity assumptions), and why differences in these are upstream of many disagreements about AI safety. None of this is particularly new, but seemed worth reiterating in the form of a short post.
Start with a cliff:
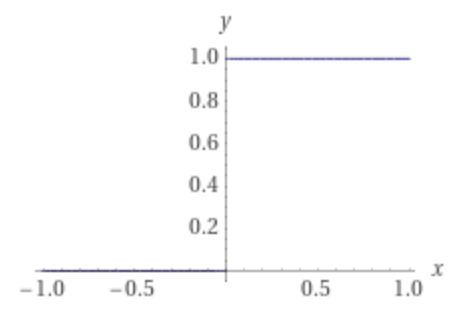
This is sometimes called the Heaviside step function. This function is actually discontinuous, and so it can represent categorical change.
In contrast, this cliff is actually continuous:
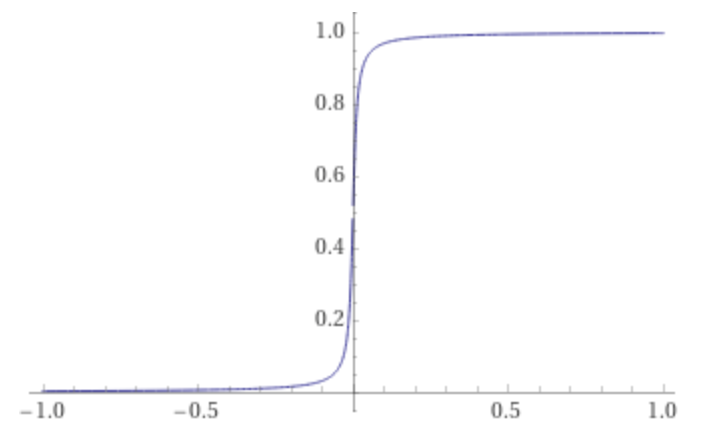
From a distance or in low resolution, it looks like a step function; it gets really steep. Yet it is fundamentally different.
Over the years, I've come to the view that intuitions about whether we live in a "continuous” or "discontinuous” world are one of the few top principal components underlying all disagreements about AI safety. This includes but goes beyond the classical continuous vs. discrete takeoff debates.
A lot of models of what can or can't work in AI alignment depends on intuitions about whether to expect "true discontinuities" or just "steep bits". This holds not just in one, but many relevant variables (e.g. the generality of the AI’s reasoning, the speed or differentiability of its takeoff).
The discrete intuition usually leads to sharp categories like:
| Before the cliff | After the cliff |
| Non-general systems. Lack the core of general reasoning, that which allows thought in domains far from training data | General systems. Capabilities generalise far |
| Weak systems - that won't kill you, but also won't help you solve alignment | Strong systems - that would help solve alignment, but unfortunately will kill you by default, if unaligned |
| Systems which may be misaligned, but aren't competently deceptive about it | System which is actively modelling you at a level where the deception is beyond your ability to notice |
| Weak acts | Pivotal acts |
| … | … |
In Discrete World, empirical trends, alignment techniques, etc usually don't generalise across the categorical boundary. The right is far from the training distribution on the left. Your solutions don't survive the generality cliff, there are no fire alarms - and so on.
Note that while assumptions about continuity in different dimensions are in principle not necessarily related, and you could e.g. assume continuity in takeoff and discontinuity in generality - in practice, they seem strongly correlated.
Deep priors over continuity versus discontinuity seem to be a crux which is hard to resolve.
My guess is intuitions about continuity/discreteness are actually quite deep-seated: based more on how people do maths, rather than specific observations about the world. In practice, for most researchers, the "intuition" is something like a deep net trained on a whole lifetime of STEM reasoning - they won't update much on individual datapoints, and if they are smart, they are often able to re-interpret observations to be in line with their continuity priors.
(As an example, compare Paul Christiano's post on takeoff speeds from 2018, which is heavily about continuity, to the debate between Paul and Eliezer in late 2021. Despite the participants spending years in discussion, progress on bridging the continuous-discrete gap between them seems very limited.)
In basically every case, continuity implies the existence of systems "somewhere in between".
The existence of such systems helps us with two fundamental difficulties of AI alignment as a field - that "you need to succeed on the first try" and "advanced AIs much more cognitively powerful than you are very difficult to align". In-between systems mean you probably have more than one try to get alignment right, and implies that bootstrapping is at least hypothetically possible - that is, aligning a system of similar power to you, and then attempting to set up a system that preserves the alignment of these early systems when we train successor systems.
A toy example:
A large model is trained, using roughly the current techniques. Apart from its performance on many other tasks, we constantly watch its performance on tripwires, a set of ''deception" or "treacherous turn" tasks. Assuming continuity, you don’t get from "the model is really bad at deception" to "you are dead" in one training step.
If things go well, at this moment we would have an AI doing interesting things, maybe on the border of generality, and has some deceptive tendencies but sort of sucks at it.
This would probably help: for example, we would gain experimental feedback on alignment ideas, which can help with finding ideas which actually work. The observations would make the "science of intelligent systems" easier. More convincing examples of deception would convince more people, and so on.
For more generality, in a different vocabulary, you can replace performance on tripwires by more general IDA-style oversight.
Continuity makes a difference: if you are in truly-discontinuous mode, you are usually doomed at the point of the jump. In the continuous mode, oversight can notice the increasing steepness of some critical variables, and slow down, or temporarily halt.
Continuity does not solve alignment.
In the continuous view, some problems may even become harder - even if you basically succeed in aligning a single human-level system, it does not mean you have won. You can easily imagine worlds, in which alignment of single systems at human-level is almost perfect – and yet in which, in the end, humans find themselves in a world where they are completely powerless and also clueless about what's actually happening with the world. Or in worlds in which the lightcone is filled with computations of little moral value, because we succeed in alignment with highly confused early 21st century moral values.
I claim that most reasoning about AI alignment and strategy is downstream of your continuity assumptions.
One reason why: once you assume a fundamental jump in one of the critical variables, you can often carry it to other variables, and soon, instead of multiple continuous variables, you are thinking in discrete categories.
Continuity is a crux for strategy. Assuming continuity, things will get weird before getting extremely weird. This likely includes domains such as politics, geopolitics, experience of individual humans... In contrast, discrete takeoff usually assumes just slightly modified politics – quite similar to today’s. So continuity can paradoxically imply that many intuitions from today won't generalise to the takeoff period, because world will be weirder.
Again, the split leads people to focus on different things – for example on "steering forces" vs. "pivotal acts".
Most of them are actually covered in Paul's writing from 2018.
One new class of objections against continuity comes from observations of jumps in capabilities in training language models. This points to a possibly important distinction between continuity in real-time variables, and continuity in learning-time variables. Which seems similar to AlphaGo and AlphaZero - where the jump is much less pronounced when the time axis is replaced by something like "learning effort spent".
It's probably worth reiterating: continuity does not imply safety. At the same time, continuity is at tension with some popular discrete assumptions about doom. For example, in Eliezer's recent post, discontinuity is a strong component of points 3, 5, 6, 7, 10, 11, 12, 13, 26, 30, 31, 34, 35 – either it's the whole point, or a significant part of its hardness and lethality.
On the continuous view, these stories of misalignment and doom seem less likely; different ones take their place.
Thanks Gavin for help with editing and references.
Thanks for the post, Jan! I follow AI Alignment debates only superficially and I had heard of the continuity assumption as a big source of disagreement, but I didn't have a clear concept of where it stemmed from and what were it's practical implications. I think your post does a very good job at grounding the concept and filling those gaps.