(This post is adapted from an academic paper. I hope forum users will excuse the explanations of some concepts that are likely common knowledge here. A PDF version of the paper can be found here.)
Longtermism is the view that the most urgent global priorities, and those to which we should devote the largest portion of our current resources, are those that focus on two things: (i) ensuring a long future for humanity, and perhaps sentient or intelligent life more generally, and (ii) improving the quality of the lives led in that long future.[1] The central argument for the longtermist's conclusion is that, given a fixed amount of a resource that we are able to devote to global priorities, the longtermist's favoured interventions have greater expected goodness than each of the other available interventions, including those that focus on the health and well-being of the current population. Longtermists might disagree on what determines how much goodness different futures contain: for some, it might be the total amount of pleasure humans experience in that future less the total amount of pain they experience; for others, the pleasures and pains of non-human sentient beings might count as well; others still might also include non-hedonic sources of value. But they agree that, once that quantity is specified, we are morally required to do whatever maximises it in expectation. And, they claim, whichever of the plausible conceptions of goodness you use, the interventions favoured by the longtermists maximise that quantity in expectation. Indeed, Greaves & MacAskill (2021) claim that the expected goodness of these interventions so far outstrips the expected goodness of the alternatives that even putatively non-consequentialist views, such as deontologism, should consider them the right priorities to fund and pursue.
In this post, I object to longtermism's assumption that, once the correct account of goodness is fixed, we are morally required to do whatever maximises that quantity in expectation. The consequentialism that underpins longtermism does not require this. It says only that the best outcomes are those that contain the greatest goodness. But that only gives the ends of moral action; it does not specify how morality requires us to pick the means to those ends. Rational choice theory is the area in which we study how to pick the best means to whatever are our ends. And, while expected utility theory is certainly one candidate account of the best means to our ends, since the middle of the twentieth century, there have been compelling arguments that it is mistaken. According to those arguments, we are permitted to take risk into account when we choose in a way that expected utility theory prohibits. For instance, we are permitted to be risk-averse and give more weight to worst-case outcomes and less weight to best-case outcomes than expected utility theory demands, and we are permitted to be risk-inclined and give more weight to best-case outcomes and less to worst-case ones than expected utility theory demands. An example: Suppose each extra unit of some commodity---quality-adjusted life years, perhaps---adds the same amount to my utility, so that that my utility is a linear function of the amount of this commodity I possess. Then most will judge it permissible for me to prefer to take 30 units of that commodity for sure rather than to take a gamble that gives me 50% chance of 100 units and a 50% chance of none, even though the expected utility of the gamble is greater. Risk-sensitive decision theories are designed to respect that judgment. I'll describe one of them in more detail in below.
How does the argument for longtermism go if we use a risk-sensitive decision theory instead of expected utility theory to pick the best means to the ends that our version of consequentialism has specified? I'll provide a detailed account below, but I'll give the broad picture here. Here, as there, I'll assume that our axiology is total human hedonism. That is, I'll assume the goodness of a state of the world is its total human hedonic value, which weighs the amount, intensity, and nature of the human pleasure it contains against the amount, intensity, and nature of the human pain it contains. Later, I ask whether the argument changes significantly if we specify a different axiology.
A future in which humanity does not go extinct in the coming century from something like a meteor strike or biological warfare might contain vast quantities of great happiness and human flourishing. But it might also contain vast quantities of great misery and wasted potential. Longtermists assume that their favoured interventions will increase the probability of the long happy future more than they will increase the probability of the long miserable future. There are a couple of routes to this conclusion. First, they might inductively infer that the historical trend towards greater total human well-being will continue, as a result of an increasing population as well as increasing average well-being, and so assume that the long happy future is currently more likely than the long miserable future; and then they might assume further that any intervention that reduces the probability of extinction will increase the probabilities of the long happy and long miserable futures in proportion to their current probabilities. Secondly, they always combine their attempts to prevent extinction with attempts to improve whatever future lives exist---that is, they might not only try to reduce the probability of extinction, but also try to decrease the probability of a miserable future conditional on there being a future at all. Either way, this ensures that, in expectation, the longtermist's intervention is better than the status quo.
However, by the lights of risk-sensitive decision theories, these considerations do not ensure that a longtermist intervention is the best means to the longtermist's goal. Indeed, for a mildly risk-averse decision theory, it is not. In fact, for a risk-averse decision theory coupled with the axiology the longtermist favours, the best means to their avowed end might be to hasten rather than prevent extinction. Since a risk-averse decision theory gives greater weight to the worst-case outcomes and less weight to the best-case outcomes than expected utility theory demands, and since the long miserable future is clearly the worst-case outcome and the long happy one the best-case, it can easily be that, when we use a risk-averse decision theory, the negative effect of the increase in the probability of the long miserable future is sufficient to swamp the positive effect of the increase in the probability of the long happy future. Such a risk-averse decision theory might declare that increasing the probability of extinction is a better means to our end than either preserving the status quo or devoting resources to the longtermist's intervention, since that reduces the probability of the long miserable future, even though it also reduces the probability of the long happy one.
So much for what a risk-averse decision theory tells us to do when it is combined with the longtermist's axiology. What reason have we for thinking that this combination determines the morally correct choice between different options? Even if we agree that such decision theories govern prudentially rational choice for some individuals, we may nonetheless think that none of them governs moral choice; we may think that some other decision theory does that, such as expected utility theory. There are at least two views on which the morally right choice for an individual is the one demanded by a risk-averse decision theory when combined with the longtermist's axiology.
On the first, for a given individual, the same decision theory governs prudential choice and moral choice. What distinguishes those sorts of choice is only the utility function you feed into the decision theory to obtain its judgment. Prudential choice requires an individual to use the decision theory that matches their attitudes to risk, and then apply it in combination with their subjective utility function. And moral choice requires them to use the same decision theory, but this time combined with a utility function that represents the correct moral axiology, such as, perhaps, a utility function that measures total human hedonic value. So, in conjunction with the conclusions of previous paragraphs, we see that, for any sufficiently risk-averse individual, the morally correct choice for that individual is not to devote resources to the longtermist intervention, but rather to hasten extinction.
On the second view, for all individuals, the same decision theory governs moral choice, and it may well be different from the one that governs any particular individual's prudential choices. This decision theory is the one that matches what we might think of as the aggregate of the attitudes to risk held by the population who will be affected by the choice in question, perhaps with particular weight given to the risk-averse members of that population. Since most populations are risk-averse on the whole, this aggregate of their attitudes to risk will likely be quite risk-averse. So, for any individual, whether they are themselves risk-averse, the morally correct choice is to hasten extinction rather than prevent it, since that is what is required by the risk-averse decision theory that matches the population's aggregate attitudes to risk.
In the remainder of the paper, I make these considerations more precise and answer objections to them.
A simple model of the choice between interventions
Let me begin by introducing a simple model of the decision problem we face when we choose how to commit some substantial amount of money to do good. I will begin by using this simple precise model to raise my concern about the recommendations currently made by longtermists. In later sections, I will consider ways in which we might change the assumptions it makes, and ask whether doing so allows us to evade my concern.
Let's assume you have some substantial quantity of money at your disposal. Perhaps you have a great deal of personal wealth, or perhaps you manage a large pot of philanthropic donations, or perhaps you make recommendations to wealthy philanthropists who tend to listen to your advice. And let's assume there are three options between which you must choose:
- (SQ) You don't spend the money, and the status quo remains.
- (QEF) You donate to the Quiet End Foundation, a charity that works to bring about a peaceful, painless end to humanity.
- (HFF) You donate to the Happy Future Fund, a charity that works to ensure a long happy future for the species by reducing extinction risks and improving the prospects for happy lives in the future.
We'll also assume that there are four possible ways the future might unfold, and their probabilities will be affected in different ways by the different options you choose:
- (lh) The long, happy future. This is the best-case scenario. Humanity survives for a billion years with a stable population of around 10 billion people at any given time.[2] During that time, medical, technological, ethical, and societal advances ensure that the vast majority of people live lives of extraordinary pleasure and fulfilment.
- (mh) The long mediocre/medium-length happy future. This is a sort of catch-all good-but-not-great option. It collects together many possible future states that share roughly the same goodness. In one, humanity survives the full billion years, some lives are happy, some mediocre, some only just worth living, many are miserable. In another, they live less long, but at a higher average level of happiness. And so on.
- (ext) The short mediocre future. Humanity goes extinct in the next century with levels of happiness at a mediocre level.
- (lm) The long miserable future. This is the worst-case scenario. Humanity survives for the full billion years with a stable population around 10 billion at any given time. During that time, the vast majority of people live lives of unremitting pain and suffering, perhaps because they are enslaved to serve the interests of a small oligarchy.
To complete our model, we must assign utilities to each of the possible states of the world, lh, mh, ext, and lm; and, for each of the three interventions, SQ, HFF, QEF, we must assign probabilities to each of the states conditional on choosing that intervention.
First, the utilities. They measure the goodness of the state of the world. For simplicity, I will assume a straightforward total human hedonist utilitarian account of this goodness. That is, I will take the goodness of a state of the world to be its total human hedonic value, which weighs the amount, intensity, and nature of the human pleasure it contains against the amount, intensity, and nature of the human pain it contains. Again, this is a specific assumption made in order to provide concrete numbers for our model. Below, I will ask what happens if we use different accounts of the goodness of a state of the world, including accounts that includes non-human animals and non-hedonic sources of value; and I will ask what happens to my argument if we use different estimates for the quantities involved here.
To specify utilities, we must specify a unit. Let's say that each human life year lived with the sort of constant extraordinary pleasure envisaged in the long happy future scenario (lh) adds one unit of utility, or utile, to the goodness of the states of the future. Then the utility of lh is utiles, since it contains human life years at the very high level of pleasure. We'll assume that the utility of the catch-all short-and-very-happy or long-and-mediocre scenario (mh) is utiles, the equivalent of a decade of human existence at the current population levels and in which each life is lived at the extremely high level of pleasure envisaged in lh; or, of course, a much longer period of existence at this population level with a much more mediocre level of pleasure. The utility of the near-extinction scenario (ext) is utiles, since it contains one hundred years lived at the same mediocre average level that, in scenario mh, when lived for a billion years, resulted in utiles. And finally the long miserable scenario (lm). Here, we assume that some lives contain such pain and suffering that they are genuinely not worth living; that is, they contribute negatively to the utility of the world. Indeed, I'll assume that it is possible to experience pain that is as bad as the greatest pleasure is good. That is, the utility of the worst case scenario is simply the negative of the utility of the best case scenario, where we are taking our zero point to be the utility of non-existence. So the utility of lm is .
Second, the probabilities of each state of the world given each of the three options, SQ, QEF, HFF. Again, I will give specific quantities here, but later I will ask how the argument works if we change these numbers.
First, let's specify the status quo. It seems clear that the long mediocre or short happy future (i.e. mh) is by far the most likely, absent any intervention, since it can be realised in so many different ways. I'll use a conservative estimate for the probability of extinction (ext) in the next century, namely, one in a hundred (). And I'll say that the long happy future, while very unlikely, is nonetheless much much more likely than the long miserable one. I'll say the long happy future (i.e. lh) is a thousand times less likely than extinction, so one in a hundred thousand (); and the long miserable future (i.e. lm) is a hundred times less likely than that, so one in ten million (). As I mentioned above, this discrepancy between the long happy future and the long miserable one is a popular assumption among longtermists. They justify it by pointing to the great increases in average well-being that have been achieved in the past thousand years; they assume that this trend is very likely to continue, and I'll grant them that assumption here. So, conditional on a long future that is either happy or miserable, a happy one is 99% certain, while a miserable one has a probability of only 1%. And, finally, I'll say that the long mediocre or short happy future (i.e. mh) mops up the rest of the probability ().
Next, suppose you donate to the Quiet End Foundation (QEF) or to the Happy Future Fund (HFF). I'll assume that both change the probability of extinction by the same amount, namely, one in ten thousand (). Donating to QEF increases the probability of extinction (ext) by that amount, while donating to HFF decreases it by the same. Then the probabilities of the other possible outcomes (lh, mh, lm) change in proportion to their prior probability.
So here are the probabilities, where
- and
- .
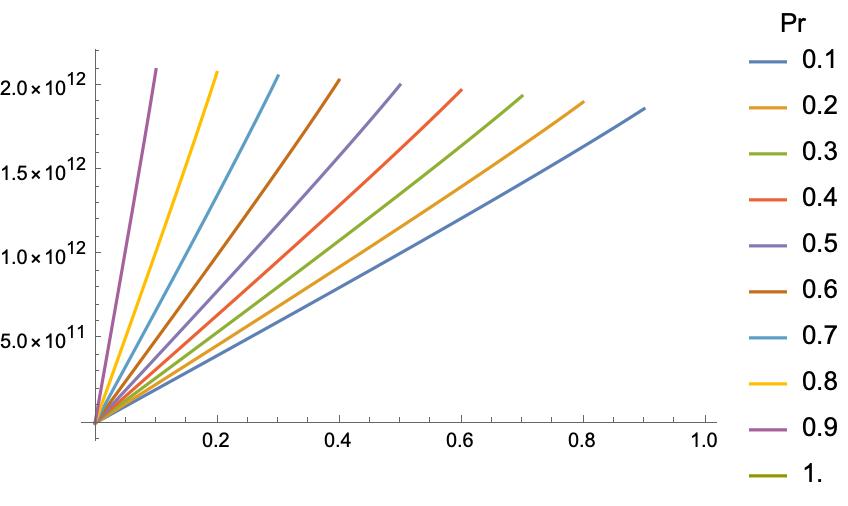
The following diagrams illustrate the expected utilities of the three interventions:
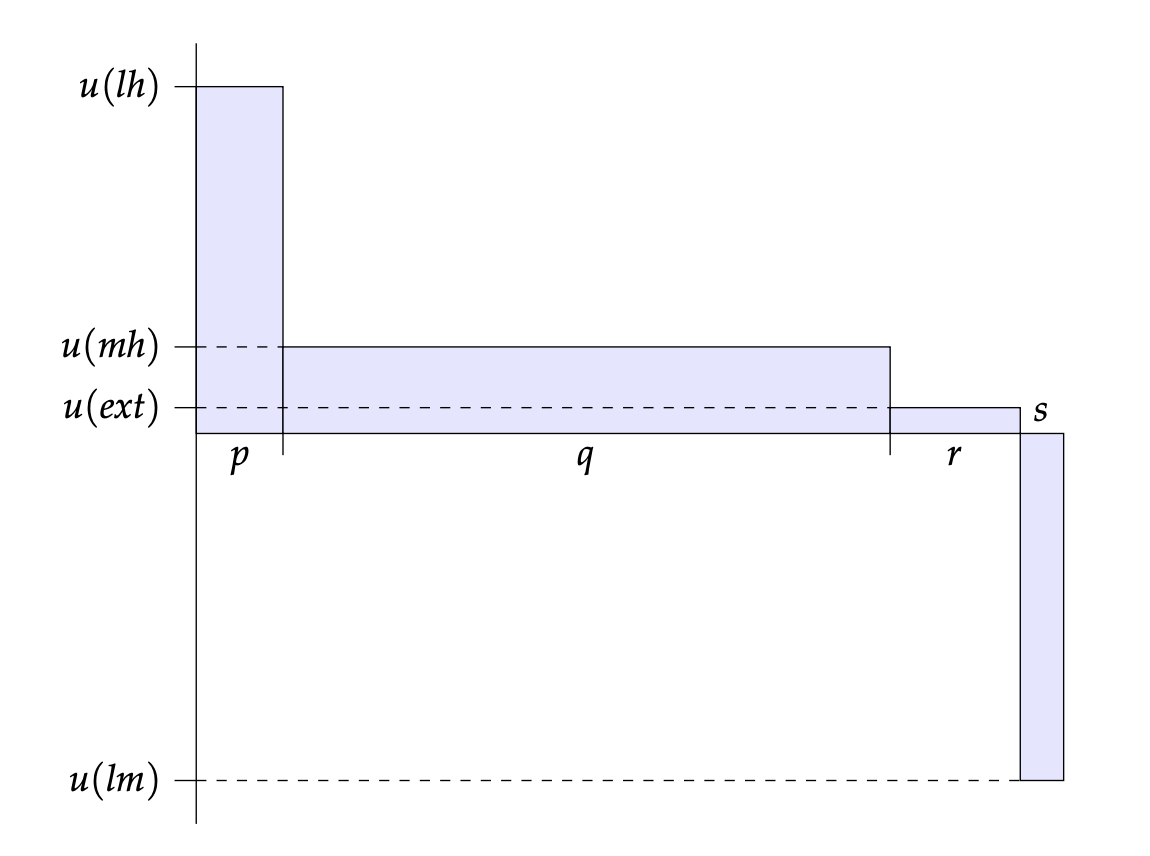
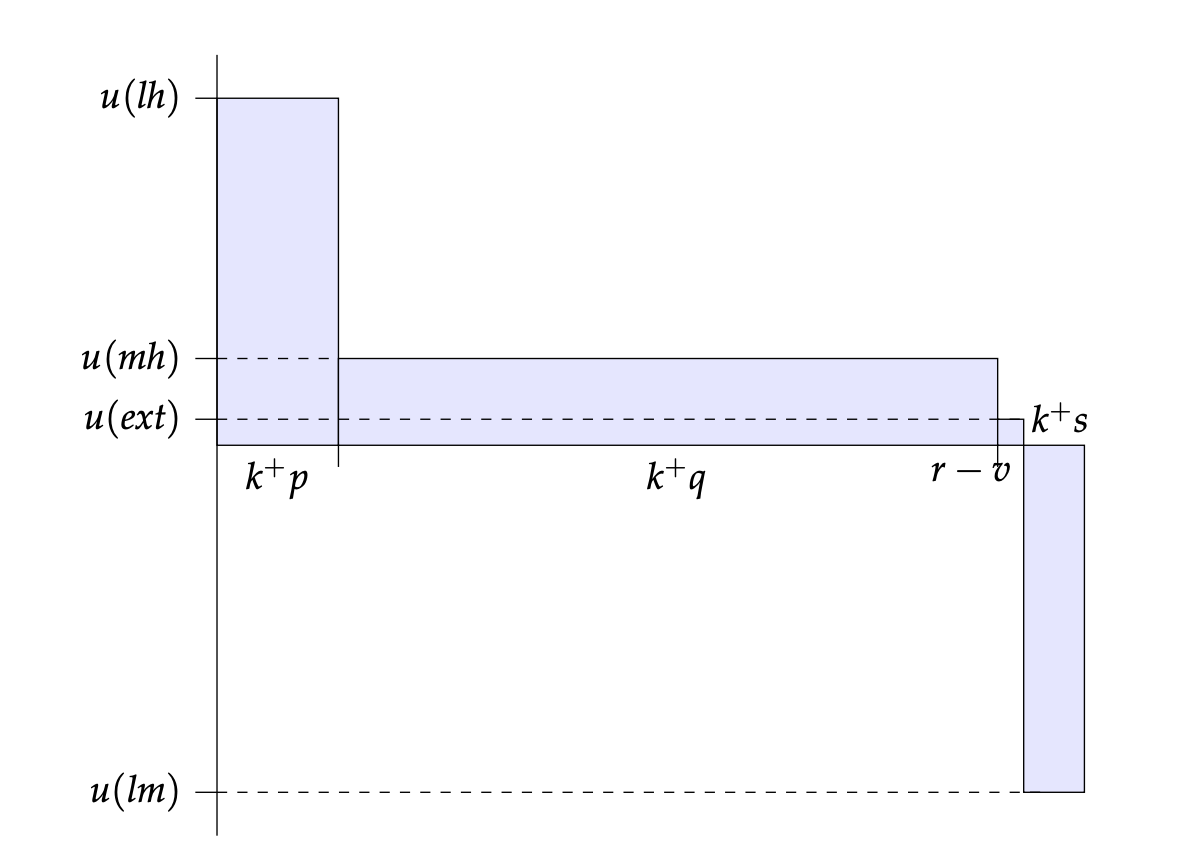
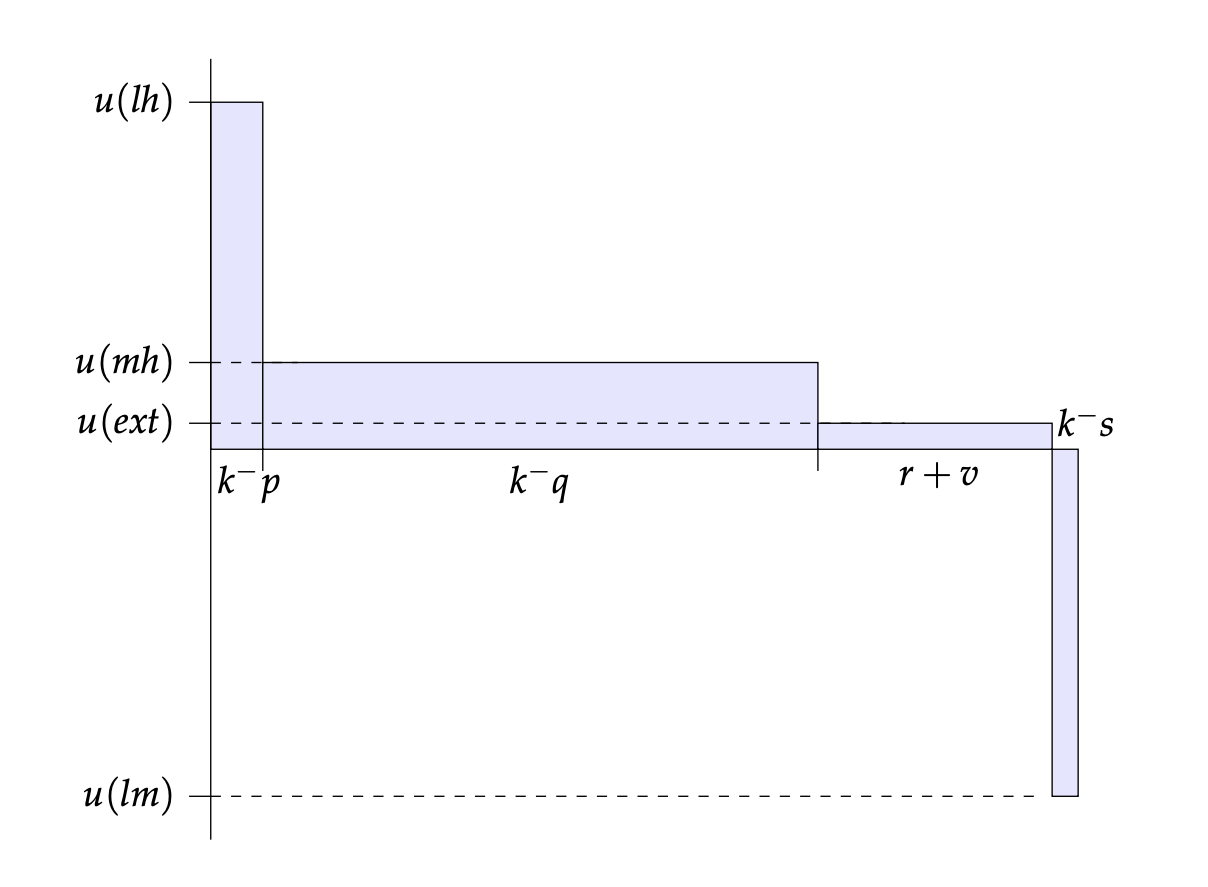
Now, this is a forest of numbers, many of which seem so small as to be negligible. But it's reasonably easy to see that the expected utility of donating to the Happy Future Fund (HFF) is greater than the expected utility of the status quo (SQ), which is greater than the expected utility of donating to the Quiet End Foundation (QEF). After all, the Quiet End Foundation takes away more probability from the best outcome (lh) than it takes away from the worst outcome (lm); and it takes away probability from the second-best outcome (mh) while adding it to the second-worst outcome (ext). So it has a negative effect in expectation. The Happy Future Fund, in contrast, adds more probability to the best outcome than to the worst outcome, and it adds to the second-best while taking away from the second-worst. So it has a positive effect in expectation.
Indeed, if you donate to the Happy Future Fund, you increase the expected utility of the world by around one billion utiles. Recall, that's one billion human life years lived at an extraordinary level of well-being. If the same amount of money could, with certainty, have saved a hundred children under five years old from a fatal illness, that would only have added around seven thousand human life years, and they would not have been lived at this very high level of well-being. So, according to the longtermist's assumption that we should do whatever maximises expected total human hedonic utility, we should donate to the Happy Future Fund instead of a charity that saves the lives of those vulnerable to preventable disease. And if you donate to the Quiet End Foundation, you decrease the expected utility of the world by around one billion utiles. Small shifts in probabilities can make an enormous difference when the utilities involved are so vast.
The upshot of this section is that, from the point of view of expected utility, the Happy Future Fund is by far the best, then the status quo, and then the Quiet End Foundation. According to the longtermist, we should do whatever maximises expected utility. And so we should donate to the Happy Future Fund.
Rational choice theory and risk
The longtermist argument sketched in the previous section concluded that we should donate to the Happy Future Fund instead of maintaining the status quo or donating to the Quiet End Foundation because doing so maximises expected goodness. In this section, I want to argue that even a classical utilitarian, who takes the goodness of a world to be the total human hedonic good that exists at that world, should not say that we are required to choose the option that maximises expected goodness. Rather, we are either permitted or required to take considerations of risk into account.
Utilitarianism, and indeed consequentialism more generally, supplies us with an axiology. It tells us how much goodness each possible state of affairs contains. And it tells us that the morally best action is the one that maximises this goodness; it is the one that, if performed, will in fact bring about the greatest goodness. But it does not tell us what the morally right action is for an individual who is uncertain about what states their actions will bring about. To supply that, we must combine consequentialism with an account of decision-making under uncertainty. As I put it above, consequentialism provides the ends of moral action; but it says nothing about the means. Since orthodox decision theory tells you that prudential rationality requires you to choose by maximising expected utility, consequentialists often say that morality requires you to choose by maximising expected goodness. However, since the middle of the twentieth century, many decision theorists have concluded that prudential rationality requires no such thing. Instead, they say, you are permitted to make decisions in a way that is sensitive to risk. In this section, I want to argue that consequentialists, including longtermists, should follow their lead.
Consider the following example.[3] Sheila is a keen birdwatcher. Every time she sees a new species, it gives her great pleasure. What's more, the amount of extra pleasure each new species brings is the same no matter many she's seen before. Her first species---a blue tit in her grandparents' garden as a child---adds as much happiness to her stock as her two hundredth---a golden eagle high above Glenshee when she's thirty. And Sheila is a hedonist who cares only for pleasure. Now suppose she is planning a birding trip for her birthday, and she must choose between two nature reserves: in one, Shapwick Heath, she's sure to see 49 new species; in the other, Leighton Moss, she'll see 100 if the migration hasn't started and none if it has. And she's 50% confident that it has started. Here's the payoff table for her choice (with one utile per bird seen):
According to expected utility theory, Sheila should choose to go to Leighton Moss, since, if each new species adds a single utile to an outcome, that option has an expected utility of 50 utiles, while Shapwick Heath has 49. And yet it seems quite rational for her to choose Shapwick Heath. In that way, she is assured of seeing some new species; indeed, she's assured of seeing quite a lot of new species; she does not risk seeing none, which she does risk if she goes to Leighton Moss. If Sheila chooses to go to Shapwick Heath, we might say that she is risk-averse, though perhaps only slightly. Leighton Moss is a risky option: it gives the possibility of the best outcome, namely, the one in which she sees 100 new species, but it also opens the possibility of the worst outcome, namely, the one in which she sees none. In contrast, Shapwick Heath is a risk-free option: it gives no possibility of the best outcome, but equally no possibility of the worst one either; it guarantees Sheila a middle-ranked option; its worst-case outcome, which is just its guaranteed outcome of 49 species is better than the worst-case outcome of Leighton Moss, which is seeing no species; but its best-case outcome, which is again its guaranteed outcome of seeing 49 species, is worse than the best-case outcome of Leighton Moss.
Standard expected utility theory says that the weight that each outcome receives before they are summed to give the expected utility of an option is just the probability of that outcome given that you choose the option. But this ignores the risk-sensitive agent's desire to take into account not only the probability of the outcome but where it ranks in the ordering of outcomes from best to worst. The risk-averse agent will wish to give greater weight to worse case outcomes than expected utility theory requires and less weight to the better case outcomes, while the risk-seeking agent will wish to give less weight to the worse cases and more to the better cases.
How might we capture this in our theory of rational choice? The most sophisticated and best developed way to amend expected utility theory to accommodate these considerations is due to Lara Buchak (2014) and it is called risk-weighted expected utility theory. Whereas expected utility theory tells you to pick an option that maximises the expected utility from the point of view of your subjective probabilities and utilities, risk-weighted expected utility theory tells you to pick an option that maximises the risk-weighted expected utility from the point of view of your subjective probabilities, utilities, and attitudes to risk. Let's see how we represent these attitudes to risk and how we define risk-weighted utility in terms of them.
Your expected utility for an option is the sum of the utilities you assign to its outcome at different possible states of the world, each weighted by the probability you assign to that possible state on the supposition that you choose the option. Your risk-weighted expected utility of an option is also a weighted sum of your utilities for it given the different possible states of the world, but the weight assigned to its utility at a particular state of the world is determined not by your probability for that state of the world given you choose it, but by the probability you'll receive at least that much utility by choosing that option, the probability you'll receive more than that utility by choosing that option, and also your attitude to risk.
Here's how it works in Buchak's theory. We model your attitudes to risk as a function that takes numbers between 0 and 1 and returns a number between 0 and 1. We assume that has three properties:
- and ,
- is strictly increasing, so that if then , and
- is continuous.
Now, to illustrate how risk-weighted expected utility theory works, suppose there are just three states of the world, , , and . Suppose is an option with the following utilities at those states:
And, on the supposition that is chosen, the probabilities of the states are these:
And, suppose is the worst case outcome for , then , and is the best case. That is, . Then the expected utility of is
So the weight assigned to the utility is the probability . Now notice that, given , the probability of a state is equal to the probability that will obtain for you at least utility less the probability that it will obtain for you more than that utility. So
Now, when we calculate the risk-weighted expected utility of , the weight for utility is the risk-transformed probability that will obtain for you at least utility less the risk-transformed probability that it will obtain for you more than that utility. So
Easily the clearest way to understand how Buchak's theory works is by considering the following diagrams. In Figure 4, the area of each rectangle gives the utility of each state of the world weighted by the weight that is applied to it in the calculation of expected utility. For instance, the area of the right-most rectangle is the utility of state multiplied by the probability of state given the option is chosen: that is, it is , or . So the total area of all the rectangles is the expected utility of the option.
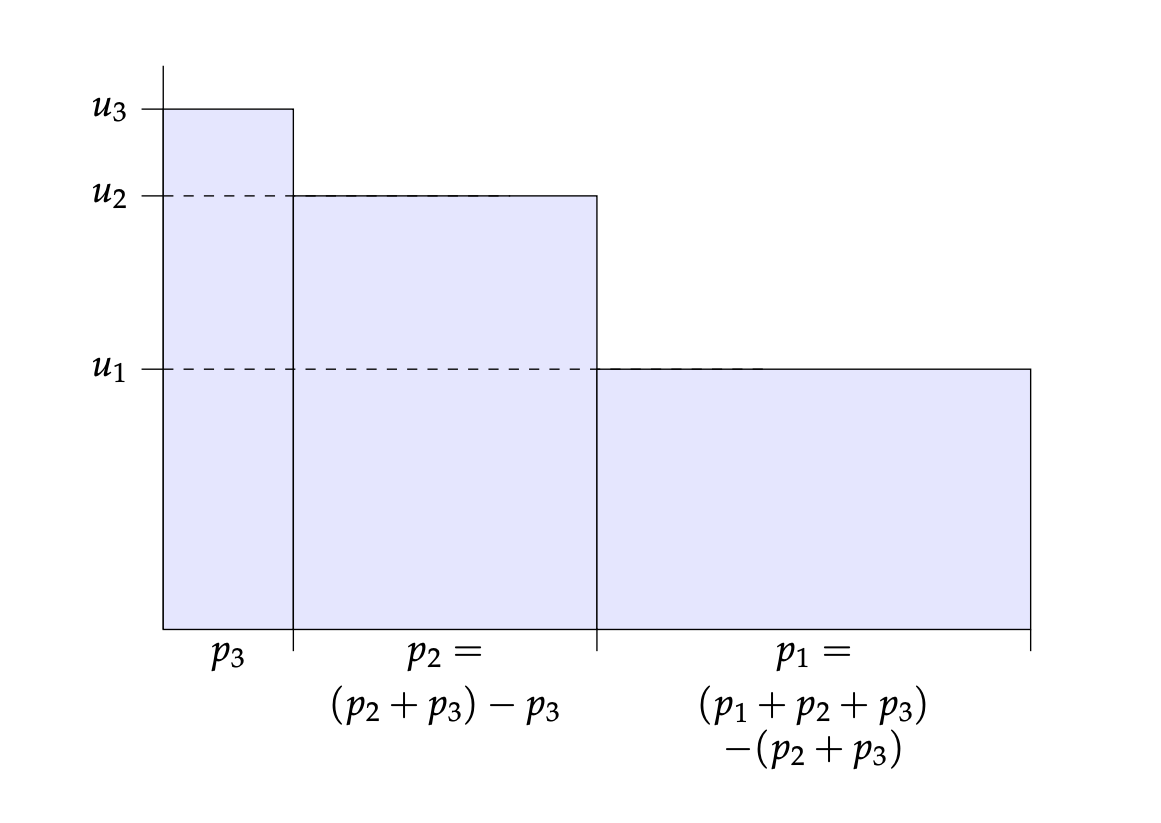
In Figure 5, the area of each rectangle gives the utility of each state weighted by the weight that is applied to it in the calculation of risk-weighted expected utility. For instance, the area of the right-most rectangle is the utility of state multiplied by the risk-transformed probability that will obtain for you at least that utility less the risk-transformed probability that it will obtain for you more than that utility: that is, it is . So the total area of all the rectangles is the risk-weighted expected utility of the option.
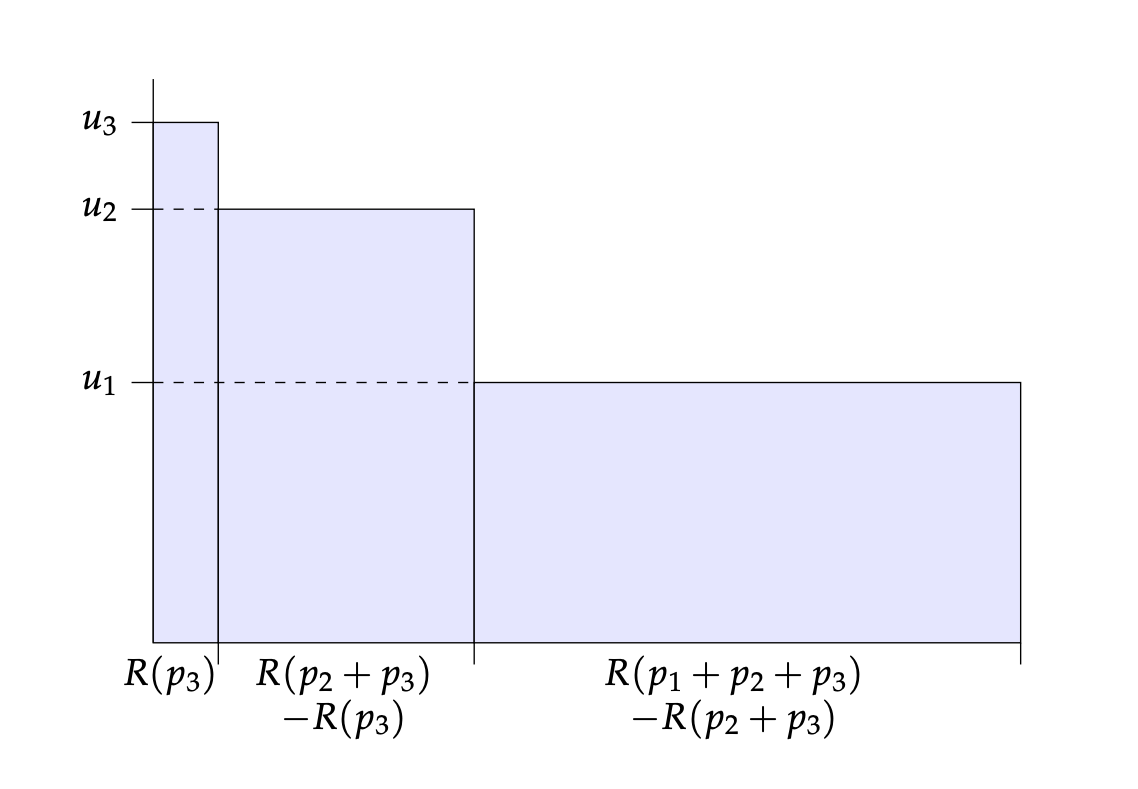
Roughly speaking, if is convex---e.g. , for ---then the individual is risk-averse, for then the weights assigned to the worse case outcomes are greater than those that expected utility theory assigns, while the weights assigned to the best case outcomes are less. If is concave---e.g. , for ---the individual is risk-inclined. And if $R$ is linear---so that ---then the risk-weighted expected utility of an option is just its expected utility, so the individual is risk-neutral.
To see an example at work, consider Sheila's decision whether to go to Shapwick Heath or Leighton Moss. If is Sheila's risk function, then the risk-weighted utility of going to Shapwick Heath is the sum of (i) its worst-case utility (i.e. 49) weighted by and (ii) its best-case utility (i.e. 49) weighted by , which is 49. And in general the risk-weighted utility of an option that has the same utility in every state of the world is just that utility. On the other hand, the risk-weighted utility of visiting Leighton Moss is the sum of (i) its worst-case utility (i.e. 0) weighted by and (ii) its best case utility (i.e. 100) weighted by , which is . So, providing , the rational option for Sheila is the safe option, namely, Shapwick Heath. for will do the trick.
Now let us apply this to the choice between doing nothing, donating to the Happy Future Fund, and donating to the Quiet End Foundation.
Suppose your risk function is for . So you are risk averse. Indeed, you have the level of risk aversion that would lead you, in Sheila's situation, to prefer a guarantee of seeing 35 new species of bird to a 50% chance of seeing 100 new species and a 50% chance of seeing none, or a guarantee of seeing 72 new species to an 80% chance of seeing 100, or a guarantee of 4 to a 10% chance of 100. So you're risk-averse, but only moderately. Then
That is, the risk-weighted expected utility of donating to the Quiet End Foundation is greater than the risk-weighted expected utility of the status quo, which is itself greater than the risk-weighted expected utility of donating to the Happy Future Fund. So, you should not donate to the Happy Future Fund, and you should not do nothing---you should donate to the Quiet End Foundation. So, if we replace expected utility theory with risk-weighted expected utility, then the effective altruist must give different advice to individuals with different attitudes to risk. And indeed the advice they give to mildly risk-averse individuals like the one just described will be to donate to charities that work towards a peaceful end to humanity.
What we together risk
The conclusion of the previous section is a little alarming. If moral choice is just rational choice but where the utility function measures the goodness that our moral axiology specifies rather than our own subjective conception of goodness, even moderately risk-averse members of our society should focus their philanthropic actions on hastening the extinction of humanity. But I think things are worse than that. I think this is not only what the longtermist should say to the risk-averse in our society, but what they should say to everyone, whether risk-averse, risk-inclined, or risk-neutral. In this section, I'll try to explain why.
To motivate the central principle used in the argument, consider the following case. A group of hikers make an attempt on the summit of a high, snow-covered mountain.[4] The route they have chosen is treacherous and they rope up, tying themselves to one another in a line so that, should one of them slip, the other will be able to prevent a dangerous fall. At one point in their ascent, the leader faces a choice. She is at the beginning of a particularly treacherous section---to climb up it is dangerous, but to climb down once you've started is nearly impossible. She also realises that she's at the point at which the rope will not provide much security, and will indeed endanger the others roped to her: if she falls while attempting this section, the whole group will fall with her, very badly injuring themselves. Due to changing weather, she must make the choice before she has a chance to consult with the group. Should she continue onwards and give the group the opportunity to reach the summit but also leave them vulnerable to serious injury, or should she begin the descent and lead the whole group down to the bottom safely?
She has climbed with this group for many years. She knows that each of them values getting to the summit just as much as she does; each disvalues severe injury just as much as she does; and each assigns the same middling value to descending now, not attaining the summit, but remaining uninjured. You might think, then, that each member of the group would favour the same option at this point---they'd all favour ascending or they'd all favour descending. But of course it's a consequence of Buchak's theory that they might all agree on the utilities and the probabilities, but disagree on what to do because they have different attitudes to risk. In fact, three out of the group of eight are risk-averse in a way that makes them wish to descend, while the remaining five wish to continue and accept the risk of injury in order to secure the possibility of attaining the summit. The leaders knows this. What should she do?
It seems to me that she should descend. This suggests that, when we make a decision that affects other people with different attitudes to risk, and when one of the possible outcomes of that decision involves serious harm to those people, we should give greater weight to the preferences of the risk-averse among them than to the risk-neutral or risk-inclined. If that's so, then it might be that the effective altruist should not only advise the risk-averse to donate to the Quiet End Foundation, but should advise everyone in this way. After all, this example suggests that the morally right choice is the rational choice when the utility function measures morally relevant goodness and the attitude to risk is obtained by aggregating the risk attitude of all the people who will be affected by the decision in some way that gives most weight to the attitudes of the risk-averse.
To the best of my knowledge, Lara Buchak is the first to try to formulate a general principle that covers such situations. Here it is:[5]
Risk Principle When making a decision for an individual, choose under the assumption that he has the most risk-avoidant attitude within reason unless we know that he has a different risk attitude, in which case, choose using his risk attitude. (Buchak 2017, 632)
Here, as when she applies the principle to a different question about long-term global priorities in her 2019 Parfit Memorial Lecture, Buchak draws a distinction between rational attitudes to risk and reasonable ones. All reasonable attitudes will be rational, but not vice versa. So very extreme risk-aversion or extreme risk-inclination will count as rational, but perhaps not reasonable, just as being indifferent to pain if it occurs on a Tuesday, but not if it occurs at another time might be thought rational but not reasonable (Parfit 1984, 124). Buchak then suggests that, when we do not know the risk attitudes of a person for whom we make a decision, we should make that decision using the most risk-averse attitudes that are reasonable, even if there are more risk-averse attitudes that are rational.
As the example of the climbers above illustrates, I think Buchak's principle has a kernel of truth. But I think we must amend it in various ways; and we must extend it to cover those cases in which (i) we choose not just for one individual but for many, and (ii) where our choice will affect different populations depending on how things turn out.
First, Buchak's principle divides the cases into only two sorts: those in which you know the person's risk attitudes and those in which you don't. It says: if you know them, use them; if you don't, use the most risk-averse among the reasonable attitudes. But of course you might know something about the other person's risk attitudes without knowing everything. For instance, you might know that they are risk-inclined, but you don't know to what extent; so you know that their risk function is concave, but you don't know which specific concave function it is. In this case, it seems wrong to use the most risk-averse reasonable risk attitudes to make your choice on their behalf. You know for sure the person on whose behalf you make the decision isn't so risk-averse as this, and indeed isn't risk-averse at all! So we might amend the principle so that we use the most risk-averse reasonable attitudes among those that our evidence doesn't rule out them having.
But even this seems too strong. You might have extremely strong but not conclusive evidence that the person affected by your action is risk-inclined; perhaps your evidence doesn't rule out that they have the most risk-averse reasonable risk attitudes, but it does make that very very unlikely. So you don't know that they are risk-inclined, but you've got very good reason for thinking they are; and you don't know that they do not have the most risk-averse reasonable risk attitudes, but you've got very good reason for thinking they don't. In this case, Buchak thinks you should nonetheless use the most risk-averse reasonable risk attitudes when you choose on their behalf. But this seems far too strong to me. It seems that you should certainly give greater weight to the more risk-averse attitudes among those you think they might have than the evidence seems to suggest; but you should not completely ignore your evidence. Having very strong evidence that they are risk-inclined, you should choose on their behalf using risk attitudes that are less risk-averse than those you'd use if your evidence strongly suggested that they are risk-averse, for instance, and less risk-averse than those you'd use if your evidence that they are risk-inclined was weaker. So evidence does make a difference, even when it's not conclusive.
Buchak objects to this approach as follows:
When we make a decision for another person, we consider what no one could fault us for, so to speak [...] [F]inding out that a majority of people would prefer chocolate [ice cream] could give me reason to choose chocolate for my acquaintance, even if I know a sizable minority would prefer vanilla; but in the risk case, finding out a majority would take the risk could not give me strong enough reason to choose the risk for my acquaintance, if I knew a sizable minority would not take the risk. Different reasonable utility assignments are on a par in a way that different reasonable risk assignments are not: we default to risk avoidance, but there is nothing to single out any utility values as default. (Buchak 2017, 631-2)
In fact, I think Buchak is right about the case she describes, but only because she specifies that there's a sizable minority that would not take the risk. But, as stated, her principle entails something much stronger than this. Even if there were only a one in a million chance that your acquaintance would reject the risk, the Risk Principle entails that you should not choose the risk on their behalf. But that seems too strong. And, in this situation, even if they did end up being that one-in-a-million person who is so risk-averse that they'd reject the risk, I don't think they could find fault with your decision. They would disagree with it, of course, and they'd prefer you chose differently, but if they know that you chose on their behalf by appealing to your very strong evidence that their risk-attitudes were not the most risk-averse reasonable ones, I think it would be strange for them to find fault with that decision. So I think Buchak is wrong to think that we default to risk-aversion; instead, the asymmetry between risk-aversion and risk-inclination is that more risk-averse possibilities and individuals should be given greater weight than more risk-inclined ones.
As it is stated, Buchak's principle applies only when you are making a decision for an individual, rather than for a group. And there again, I think the natural extension of the principle should be weakened. It seems that we do not consider immoral any decision on behalf of a group that goes against the preferences of the most risk-averse reasonable person possible, or even against preferences of the most risk-averse reasonable person in that group. For instance, it seems perfectly reasonable to be so risk-averse that you think the dangers of nuclear power outweigh the benefits, and yet it is morally permissible for a policymaker to pursue the project of building nuclear power stations because, while they give extra weight to the more risk-averse in the society affected, that isn't sufficient to outweigh the preferences of the vast majority who think the benefits outweigh the dangers.
Another crucial caveat to Buchak's principle is that it seems to apply only to decisions in which there is a risk of harm. Suppose that I must choose, on behalf of myself and my travelling companion, where we will go for a holiday. There are two options: Budapest and Bucharest. I know that going to Budapest will be very good, while I don't know whether Bucharest will be good or absolutely wonderful, but I know those are the possibilities. Then the risk-averse option is Budapest, and yet even if my travelling companion is risk-averse while I am risk-inclined, it seems that I do nothing morally wrong if I choose the risky option of Bucharest as our destination. And the reason that this is permissible is that none of the possible outcomes involves any harm---the worst that can happen is that our holiday is merely good rather than very good or absolutely wonderful.
Finally, in many decisions, there is a single population who will be affected by your actions regardless of how the world turns out, and in those cases, it is of course the risk attitudes of the people in that population you should aggregate to give the risk attitudes you'll use to make the decision on their behalf, weighting the more risk-averse more, as I've argued. But in some cases, and for instance in the choice between the Quiet End Foundation and the Happy Future Fund, different populations will be affected depending on how the world turns out: the world will contain different people in the four situations lh, mh, ext, and lm. How then are we to combine uncertainty about the population affected with information about the distribution of risk attitudes among those different possible populations? I think this is going to be a difficult question in general, just as it'll be difficult to formulate principles that govern situations in which there's substantial uncertainty about the distribution of risk attitudes in the population affected, but I think we can say one thing for certain: suppose it's the case that, for any of the possibly affected populations, were they the only population affected, you'd not choose the risky option; then, in that case, you shouldn't choose the risky option when there's uncertainty about which population will be affected.
Bringing all of this together, let's try to reformulate Buchak's risk principle:
Risk Principle*
- Choosing on behalf of an individual when you're uncertain about their risk attitudes When you make a decision on behalf of another person that might result in harm to that person, you should use a risk attitude obtained by aggregating the risk attitudes that your evidence says that person might have. And, when performing this aggregation, you should pay attention to how likely your evidence makes it that they have each possible risk attitude, but you should also give greater weight to the more risk-averse attitudes and less weight to the more risk-inclined ones than the evidence suggests.
- Choosing on behalf of a group when there's diversity of risk attitudes among its members When you make a decision on behalf of a group of people that might result in harm to the people in that group, you should use a risk attitude obtained by aggregating the risk attitudes that those people have. And, when performing this aggregation, you should give greater weight to more risk-averse individuals in the group.
- Choosing on behalf of a group when there's uncertainty about the risk attitudes of its members either because a single population is affected but you don't know the distribution of risk attitudes within it, or because you don't know which population will be affected When you make a decision on behalf of a group of people that might result in harm to the people in that group, and you are uncertain about the distribution of the risk attitudes in that group, then you should work through each of the possible populations with their distributions of risk attitudes in turn, perform the sort of aggregation we saw in (ii) above, then take each of those aggregates and aggregate those, this time paying attention to how likely your evidence makes each of the populations they aggregate, but also giving more weight to the more risk-averse aggregates and less weight to the more risk-inclined ones than the evidence suggests.
Like Buchak's, this version is not fully specified. For Buchak's, that was because the notion of reasonable risk attitudes remained unspecified. For this version, it's because we haven't said precisely how to aggregate risk attitudes nor how to determine exactly what extra weight an attitude receives in such an aggregation because it is risk-averse. I will leave the principle underspecified in this way, but let me quickly illustrate the sort of aggregation procedure we might use. Suppose we have a group of individuals and their individual risk attitudes are represented by the Buchakian risk functions . Then we might aggregate those individual risk functions to give the aggregate risk function that represents the collective risk attitudes of the group by taking a weighted average of them: that is, the risk function of the group is for some weights , each of which is non-negative and which together sum to 1. Then we might ensure that is greater the more risk averse (and thus convex) is.
In any case, underspecified though the Risk Principle* is in various ways, I think it's determinate enough to pose the problem I want to pose. Many people are quite risk averse; indeed, the empirical evidence suggests that most are (MacCrimmon & Larsson 1979, Rabin & Thaler 2001, Oliver 2003). We should expect that to continue into the future. So each of the possible populations affected by my choice of where to donate my money---that is, the populations that inhabit scenarios lh, mh, ext, and lm, respectively---are likely to include a large proportion of risk-averse individuals. And so the third clause of the Risk Principle*---that is, (iii)---might well say that I should choose on their behalf using an aggregated risk function that is pretty risk-averse, and perhaps sufficiently risk-averse that it demands we donate to the Quiet End Foundation rather than the Happy Future Fund or the Against Malaria Foundation or whatever other possibilities there are.
What I have offered, then, is not a definitive argument that the longtermists must now focus their energies on bringing about the extinction of humanity and encouraging others to donate their resources to helping. But I hope to have made it pretty plausible that this is what they should do.
How should we respond to this argument?
How should we respond to these two arguments? The first is for the weaker conclusion that, for many people who are risk averse, the morally correct choice is to donate to the Quiet End Foundation. The second is for the stronger conclusion that, for everyone regardless of attitudes to risk, the morally correct choice is to donate in that way. Here's the first in more detail:
(P1) The morally correct choice for you is the one required by the correct decision theory when that theory is applied using certain attitudes of yours and certain attitudes set by morality.
(P2) The correct decision theory is risk-weighted expected utility theory.
(P3) When you apply risk-weighted expected utility theory in ethics, you should use your own credences and risk attitudes, providing they're rational and reasonable, but you should use the moral utilities, which measure the morally relevant good.
(P4) Given your current evidential and historical situation, if you are moderately risk-averse, you maximise risk-weighted expected moral utility by choosing to donate to the Quiet End Foundation rather than by doing nothing or donating to the Happy Future Fund.
Therefore,
(C) If you are even mildly risk-averse, the morally correct choice for you is to donate to the Quiet End Foundation.
And the second:
(P1)] The morally correct choice for you is the one required by the correct decision theory when that theory is applied using certain attitudes of yours and certain attitudes set by morality.
(P2) The correct decision theory is risk-weighted expected utility theory.
(P3') When you apply risk-weighted expected utility theory in ethics, you should use your own credences, providing they're reasonable and rational, but you should use the utilities specified by moral axiology, and you should use risk attitudes obtained by aggregating actual and possible risk attitudes in the populations affected in line with the Risk Principle*.
(P4') Given your current evidential and historical situation, you maximise the risk-weighted expected moral utility by choosing to donate to the Quiet End Foundation rather than by doing nothing or donating to the Happy Future Fund.
Therefore,
(C')] Whether you are risk-averse or not, the morally correct choice for you is to donate to the Quiet End Foundation.
Changing the utilities: conceptions of goodness
One natural place to look for the argument's weakness is in its axiology. Throughout, we have assumed the austere, monistic conception of morally relevant goodness offered by the hedonist utilitarian and restricted only to human pleasure and pain.
So first, we might expand the pale of moral consideration to include non-human animals and non-biological sentient beings, such as artificial intelligences, robots, and minds inside computer simulations. But, this is unlikely to change the problem significantly. It only means that there are more minds to contain great pleasure in the long happy future (lh), but also more to contain great suffering in the long miserable one (lm). And of course there is the risk that humanity continues to give non-human suffering less weight than we should, and as a result non-human animals and artificial intelligences are doomed to live miserable lives, just as factory-farmed animals currently do. While longtermists are surely right that the average well-being of humans has risen dramatically over the past few centuries, the average well-being of livestock has plummeted at the same time as their numbers have dramatically increased. If we simply multiply the utility of each outcome by the same factor to reflect the increase in morally relevant subjects, this will change nothing, since risk-weighted expected utility comparisons are invariant under positive linear transformations of utility---you can scale everything up by a factor and add some fixed amount and everything remains the same. And if we increase the utility of lh and mh, decrease the utility of lm, and leave the utility of ext untouched, on the grounds that the extra beings we wish to include within the moral pale are artificial intelligences that are yet to exist and so won't exist in significant numbers within future ext, then this in fact merely widens the gap between the risk-weighted expected utility of donating to the Quiet End Foundation and the risk-weighted utility of donating to the Happy Future Fund. And the same happens if we entertain the more extreme estimates for the possible number of beings that might exist in the future, which arise because we colonise beyond Earth.
Second, we might change what contributes to the morally relevant goodness of a situation. For instance, we might say that there are features of a world that contains flourishing humans that add goodness, while there are no corresponding features of a world that contains miserable humans that add the same badness. One example might be the so-called higher goods of aesthetic and intellectual achievements. In situation lh, we might suppose, people will produce art, poetry, philosophy, music, science, mathematics, and so on. And we might think that the existence of such achievements adds goodness over and above the pleasure that people experience when they engage with them; they somehow have an intrinsic goodness as well as an instrumental goodness. This would boost the goodness of lh, but it leaves the badness of lm unchanged, since the absence of these goods is neutral, and there is nothing that exists in lm that adds further badness to lm in the way these higher goods add goodness to lh. If these higher goods add enough goodness to lh without changing the badness of lm, then it may well be that even the risk-averse will prefer the Happy Future Fund over the Quiet End Foundation. See Figure 6 for the effects of this on the difference between the risk-weighted expected utility of the Quiet End Foundation and the risk-weighted expected utility of the Happy Future Fund.
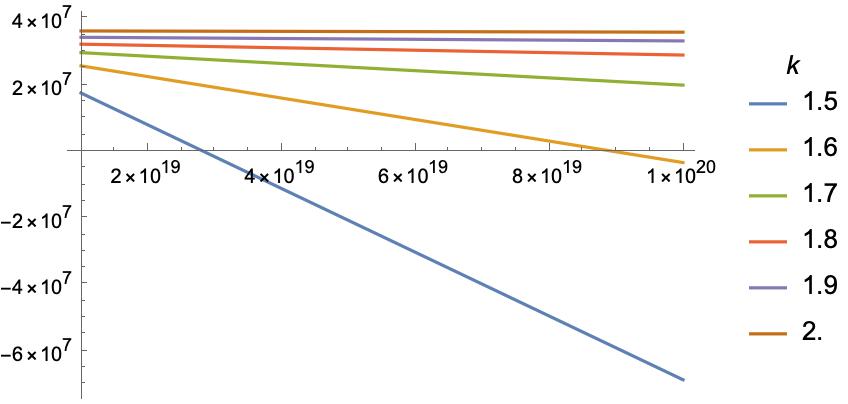
Of course, the most obvious move in this direction is simply to assume that the existence of humanity adds goodness beyond the pleasure or pain experienced by the humans who exist. Or perhaps it's not the existence of humans specifically that adds the value, but the existence of beings from some class to which humans belong, such as the class of intelligent beings or moral agents or beings capable of ascribing meaning to the world and finding value in it. Again, the idea is that the existence of these creatures is good independent of the work to which they put their special status. So, as for the case of the higher goods, this would add goodness to lh, which contains such creatures, but not only would it not add corresponding badness to lm; it would in fact add goodness to lm, since lm contains these beings who boast the special status. And it might add enough goodness to lh and lm that it would reverse the risk-averse person's preferences between the charities.
My own view is that it is better not to think of the existence of intelligent beings or moral agents as adding goodness regardless of how they deploy that intelligence or moral agency. Rather, when we ascribe morally relevant value to the existence of humans, we do so because of their potential for doing things that are valuable, such as creating art and science, loving and caring for one another, making each other happy and fulfilled, and so on. But in scenario lm, the humans that exist do not fulfil that potential, and since that scenario specifies all aspects of the world's history---past, present, and future---there is no possibility that they will fulfil it, and so there is no value added to that scenario by the fact that beings exist in it that might have done something much better. And, at least if we suppose that the misery in scenario lm is the result of human cruelty or lack of moral care, we might think the fact that the misery is the result of human immorality makes it have lower moral utility.
For those who prefer an axiology on which it is not the hedonic features of a situation that determine its morally relevant goodness, but rather the degree to which the preferences of the individuals who exist in that situation are satisfied, you might hope to appeal to the fact that people have a strong preference for humanity to continue to exist, which gives a substantial boost to lh and lm, perhaps enough to make the Happy Future Fund the better option. But I think this only seems plausible because we've grained our preferences too coarsely. People do not have a preference for humanity to continue to exist regardless of how humans behave and the quality of the lives they live. They have a preference for humanity continuing in a way that is, on balance, positive. So adding the good of preference satisfaction to the hedonic good will likely boost the goodness of lh, since lh contains a lot of pleasure and also satisfies the preferences of nearly everyone, but it will also boost the badness of lm, since lm contains a lot of pain and also thwarts the preferences of nearly everyone.
The same is true if we appeal to obligations that we have to those who have lived before us (Baier 1981). At this point, we step outside the consequentialist framework in which longtermist arguments are usually presented, and into a deontological framework. But we might marry these two approaches and say that obligations rule out certain options from the outset and then consequentialist reasoning enters to pick between the remaining ones. Here, we might think that past generations created much of what they did and fought for what they did and bequeathed to us the fruits of their labours and their sacrifices on the understanding that humanity would continue to exist. And you might think that, by benefitting from what they bequeathed to us---those goods for which they laboured and which they made sacrifices to obtain---we take on an obligation not to go against their wishes and bring humanity to an end. But, as before, I think what they really wished was that humanity continue to exist in a way they considered positive. And so obligations to them don't rule prohibit ending humanity if by doing so you avoid a universally miserable human existence.
Changing the probabilities
In the previous section, we asked how different conceptions of goodness might change the utilities we've assigned to the four outcomes lh, mh, ext, lm in our model. Now, we turn to the probabilities we've posited.
As I mentioned above, I used a conservative estimate of for the probability of near-term extinction. Toby Ord (2020) places the probability at . Users of the opinion aggregator Metaculus currently place it at .[6] How do these alternative probabilities affect our calculation? Figure 7 gives the results.
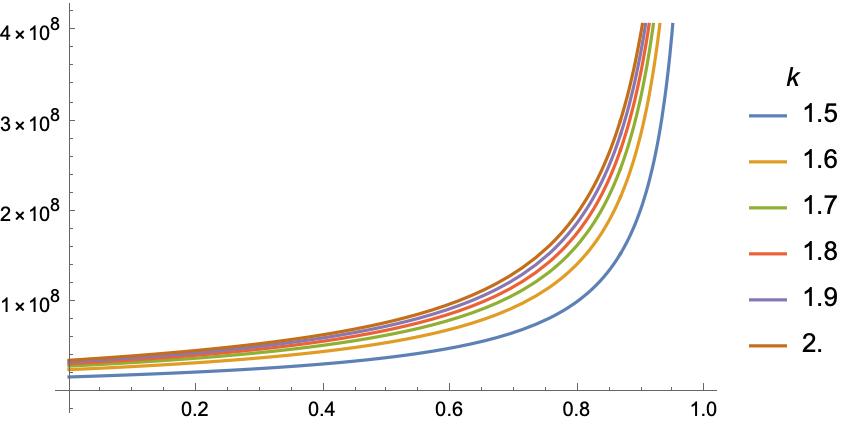
The answer is that, for any risk function with , our conclusion that donating to the Quiet End Foundation (QEF) is better than donating to the Happy Future Fund (HFF) is robust under any change in the probability of extinction.
Next, consider the change in the probabilities that we can affect by donating either to the Happy Future Fund or the Quiet End Foundation. I assumed that, either way, we'd change the probability of extinction by ---the Happy Future Fund decreases it by that amount; the Quiet End Foundation increases it by the same. But perhaps our intervention would have a larger or smaller effect than that. Figures 8 and 9 illustrate the effects. Again, our conclusion is robust.
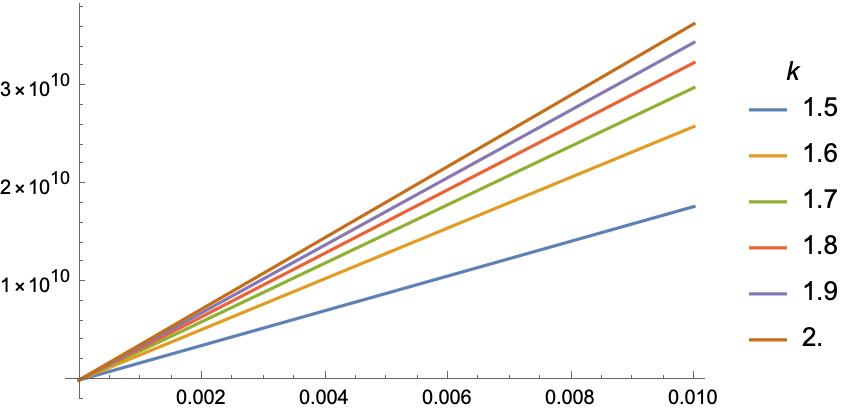
Finally, in our original model we assume that, after the intervention, the conditional probabilities of the three non-extinction options conditional on extinction not happening remained unchanged. The probability we remove from ext by donating to the Happy Future Fund is distributed to lh, mh, and lm in proportion to their prior probabilities. But we might think that, as well as reducing the probability of extinction, some of our donation might go to improving the probability of the better futures conditional on there being any future at all. But of course, if that's what the Happy Future Fund are going to do with our money, the Quiet End Foundation can do the same with the same amount of money. As well as working to increase the probability of extinction, some of our donation to the Quiet End Foundation might go towards improving the probability of the better futures conditional on there being any future at all. Above, we assumed that the probabilities of lh, mh, and lm, given that you donate to the Quiet End Foundation, are just their prior probabilities multiplied by the same factor . And similarly the probabilities of lh, mh, and lm given that you donate to the Happy Future Fund are just their prior probabilities multiplied by the same factor . But now suppose that the probability of lh given QEF is its prior probability multiplied by a factor , the probability of mh given QEF is its prior probability multiplied by factor , and the prob of lm given QEF is its prior probability multiplied by factor . And similarly for HFF, but with , , and , respectively. Then for what values of is QEF still better than HFF? Figure 10 answers the question.
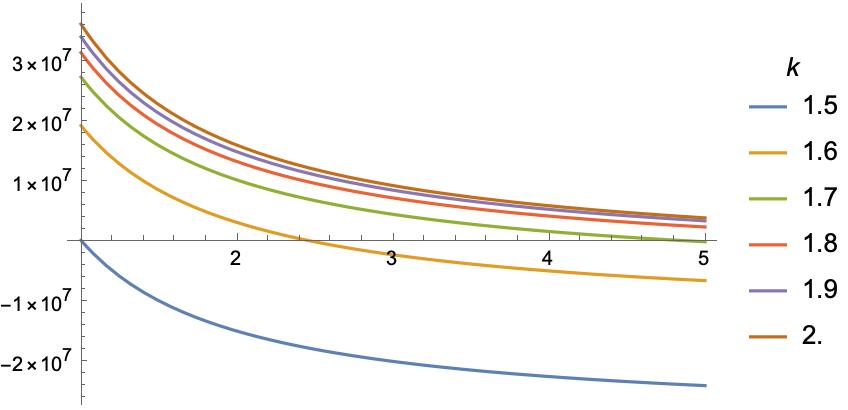
For our original risk function , HFF quickly exceeds QEF. But for an only slightly more risk-averse individual, with risk function , QEF beats out HFF for up to nearly .
This is the first time we've anything less than robustness in our conclusion about the relative merits of QEF and HFF. It illustrates an important point. While the result that risk-averse individuals should prefer QEF to HFF is reasonably robust for risk-aversion represented by , there are certain ways in which we might change our model so that this robustness disappears, and the ordering of the two interventions becomes very sensitive to certain features, since as degrees of risk-aversion. For instance, you might think that the lesson of Figure 10 is that our longtermist interventions should balance more towards improving the future conditional on its existence and less towards ensuring the existence of the future. But we see that, for , even favours QEF. So, if this is the risk function we're using to make moral choices, the rebalancing will have to be very dramatic in order to favour HFF.
Overturning unanimous preference
One apparent problem with letting risk-sensitive decision theory govern moral choice is that those choices may thereby end up violating the so-called Ex Ante Pareto Principle, which says that it's never morally right to choose one option over another when the second is unanimously preferred to the first by those affected by it.[7]
Suppose Ann is risk-neutral: that is, she values options at their expected utility. And suppose Bob is a little risk-averse: he value options at their risk-weighted expected utility with risk function . Both agree that the coin in my hand is fair, with a 50% chance of landing heads and a 50% chance of landing tails. I must make a decision on behalf of Ann and Bob. Two options are available to me: and . If I choose , Ann will face a gamble that leaves her with 12 utiles if the coin lands heads and 8 utiles if it lands tails, while Bob will be left with 0 utiles either way.[8] If I choose , on the other hand, Bob will face the gamble instead, leaving him with 12 utiles if heads and 8 if tails, while Ann will be left with 1 utile either way. Their utilities are given in the following tables:
Then Ann prefers to , since has an expected utility of 2 utiles for her, while has an expected utility of 1 utile. And Bob prefers to , since has risk-weighted utility of 0 utiles, while has a risk-weighted expected utility of . But note: the total utility of is 12 is heads and if tails, while the total utility of is 13 if heads and if tails. So, if we make our moral choices using risk-weighted expected utility theory combined with a utility function that measures the total utility obtained by summing Ann's utility and Bob's, we will choose , which overturns their unanimous preferences.
At first sight, this seems worrying for our proposal that the morally correct choice is the one recommended by risk-weighted expected utility theory when combined with a utility function that measures morally relevant goodness. But, it's easy to see that there's nothing distinctive about our proposal that causes the worry. After all, any plausible decision theory, when coupled with an axiology that takes the value of an outcome to be the total utility present in the outcome, will choose over , for, in the jargon of decision theory, strongly dominates ---that is, is guaranteed to be better than ; however the world turns out, is better than ; if the coin lands heads, has greater total utility, and if the coin lands tails, has the greater total utility. So it doesn't count against the Risk Principle* or the use of risk-weighted expected utility theory for moral choice that they lead to violations of the Ex Ante Pareto Principle. Any plausible decision theory will do likewise. Indeed, the longtermist's favoured theory, on which we should maximise expected total utility will favour over .
What is really responsible for the issue here is that we permit individuals to differ in their attitudes to risk. It is because Ann and Bob differ in these attitudes that we can find a decision problem in which they both prudentially prefer one option to another, while the latter option is guaranteed to give greater total utility than the former.[9] [EDIT: In fact, as Jake Nebel points out in the comments, even if Ann and Bob were to have the same non-neutral attitude to risk, we'd be able to find cases like the one here in which total utilitarianism forces us to overturn unanimous preferences. See (Nebel 2020)] But we can't very well say that an individual's attitudes to risk are irrational or prohibited purely on the grounds that, by having them they ensure that maximising expected or risk-weighted expected total utility will lead to a violation of Ex Ante Pareto.
Conclusion
I've presented arguments for two conclusions, one stronger than the other: first, if you are sufficiently averse to risk, and you wish to donate some money to do good, then you should donate it to organisations working to hasten human extinction rather than ones working to prevent it; secondly, whether or not you are averse to risk, this is what you should do. And I've considered some responses and I've tried to show that the arguments still stand in the light of them.
What, then, is the overall conclusion? I confess, I don't know. What I hope this paper will do is neither make you change the direction of your philanthropy nor lead you to reject the framework of effective altruism in which these arguments are given. Rather, I hope it will encourage you to think more carefully about how risk and our attitudes towards it should figure in our moral decision-making.[10]
References
Blessenohl, S. (2020). Risk Attitudes and Social Choice. Ethics, 130, 485–513.
Bostrom, N. (2013). Existential Risk Prevention as Global Priority. Global Policy, 4(1), 15-31.
Buchak, L. (2013). Risk and Rationality. Oxford, UK: Oxford University Press.
Buchak, L. (2017). Taking Risks Behind the Veil of Ignorance. Ethics, 127(3), 610–644.
MacAskill, W. (2022). What We Owe the Future. London, UK: Basic Books.
Nebel, J. (2020). Rank-Weighted Utilitarianism and the Veil of Ignorance. Ethics, 131, 87-106.
Ord, T. (2020). The Precipice: Existential Risk and the Future of Humanity. London, UK: Bloomsbury.
Parfit, D. (1984). Reasons and Persons. Oxford University Press.
Rozen, I. N., & Fiat, J. (ms). Attitudes to Risk when Choosing for Others. Unpublished manuscript.
- ^
The idea has a long history, running through the Einstein-Russell Manifesto and a thought experiment described by Derek Parfit on the last few pages of Reasons and Persons (Parfit, 1984). It has been developed explicitly over the past decade by Beckstead (2013), Bostrom (2013), Ord (2020), Greaves & MacAskill (2021), MacAskill (2022).
- ^
Throughout, I will take 1 billion to be .
- ^
For further motivations for risk-sensitive decision theories, see Buchak (2014, Chapters 1 and 2). The shortcomings of expected utility theory were first identified by Maurice Allais (1953). He presented four different options, and asked us to agree that we would prefer the first to the second and the fourth to the third. He then showed that there is no way to assign utilities to the outcomes of the options so that these preferences line up with the ordering of the options by their expected utility. For a good introduction, see (Steele and Stefánsson 2020, Section 5.1).
- ^
Thanks to Philip Ebert for helping me formulate this example!
- ^
Cf. also Rozen & Fiat (ms)
- ^
https://www.metaculus.com/questions/578/human-extinction-by-2100/. Retrieved 2nd August 2022.
- ^
Thank you to Teru Thomas for pressing me to consider this objection.
- ^
As always, we assume that the interpersonal utilities of Ann and Bob can be compared and measured on the same scale.
- ^
Indeed, as Simon Blessenohl (2020) shows, all that is really required is that there is a pair of options for which one individual prefers the first to the second while the other individual prefers the second to the first. And that might arise because of different attitudes to risk, but it might also arise because of different rationally permissible credences in the same proposition.
- ^
I'd like to thank Teru Thomas, Andreas Mogensen, Hayden Wilkinson, Tim Williamson, and Christian Tarney for extraordinarily generous comments on an earlier draft of this material; Marina Moreno and Adriano Mannino for long and extremely illuminating discussions; and audiences in Bristol, Munich, Oxford, and the Varieties of Risk project for their insightful questions and challenges.

Boring meta comment on the reception of this post: Has anyone downvoting it read it? I don't see how you could even skim it without noticing its patent seriousness and the modesty of its conclusion.
(Pardon the aside, Richard; I plan to comment on the substance in the next few days.)
Thanks, Gavin! I look forward to your comment! I'm new to the forum, and didn't really understand the implications of the downvotes. But in any case, yes, the post is definitely meant in good faith! It's my attempt to grapple with a tension between my philanthropic commitments and my views on how risk should be incorporated in both prudential and moral decision-making.
Welcome to the EA forum Richard!
Three comments:
Should we use risk-averse decision theories?
Note that risk-weighted utility theories (REUT) are not the only way of rationalising Sheila’s decision-making. For example, it might be the case that when Sheila goes to Leighton Moss and sees no birds, she feels an immense regret, because post-hoc she knows she would have been better off if she'd gone to Shapwick Heath. So the decision matrix looks like this, where δ is the loss of utility due to Sheila's regret at the decision she made.
That is, I have re-described the situation such that even using expected utility theory, for large enough δ, Sheila is still being rational to go to Shapwick Heath. Of course, where Sheila would not feel such regret (δ= 0), or the regret would not be large enough to change the result, then on expected utility theory (EUT) Sheila is not acting rationally.
It’s not clear to me how to choose between EUT and REUT for describing situations like this. My intuition is that, if upon making the decision I could immediately forget that I had done so, then I would not succumb to the Allais paradox (though I probably would succumb to it right now). So I’m weakly inclined to stick with EU. But I haven't thought about this long and hard.
The relevance to AI strategy
Considerations about risk-aversion are relevant for evaluating different AGI outcomes and therefore are relevant for determining AI strategy. See Holden Karnofsky's Questions about AI strategy: ‘insights about how we should value “paperclipping” vs. other outcomes could be as useful as insights about how likely we should consider paperclipping to be’. In this case "other outcomes" would include the long miserable and the long happy future.
Pushing back on the second conclusion
While I agree with the first of the conclusions (“if you are sufficiently averse to risk, and you wish to donate some money to do good, then you should donate it to organisations working to hasten human extinction rather than ones working to prevent it”), I don’t agree with the second (“whether or not you are averse to risk, this is what you should do”).
In essence, I think the total hedonist utilitarian has no intrinsic reason to take into account the risk-preferences of other people, even if those people would be affected by the decision.
To see this, imagine that Sheila is facing a classic scenario in moral philosophy. A trolley is on track to run over five people, but Sheila has the chance to divert the trolley such that it only runs over one person. Sheila is a total hedonist utilitarian and believes the world would be better off if she diverted the trolley. We can easily imagine Sheila’s friend Zero having different moral views and coming to the opposite conclusion. Sheila is on the phone to Zero while she is making this decision. Zero explains the reasons he has for his moral values and why he thinks she should not divert the trolley. Sheila listens, but by the end is sure that she does not agree with Zero’s axiology. Her decision theory suggests she should act so as to maximise the amount of utility in the world and divert the trolley. Given her moral values, to do otherwise would be to act irrationally by her own lights.
If Sheila is risk-neutral and is the leader in the rock-climbing example above, then she has no intrinsic reason to respect the risk preferences of those she affects. That is, the total hedonist utilitarian must bite the bullet and generally reject Pettigrew’s conclusion from the rock-climbing example that "she should descend.” Of course, in this specific case, imposing risks on others could annoy them and this annoyance could plausibly outweigh the value to the total hedonist utilitarian of carrying on up the mountain.
I think there are good deontological reasons to intrinsically respect the risk-preferences of those around you. But to the extent that the second argument is aimed at the total hedonist utilitarian, I do not think it goes through. For a longer explanation of this argument, see this essay where I responded to an earlier draft of this paper. And I'd love to hear where people think my response goes wrong.
Thanks for the comment, Alejandro, and apologies for the delay responding -- a vacation and then a bout of covid.
On the first: yes, it's definitely true that there are other theories besides Buchak's that capture the Allais preferences, and a regret averse theory that incorporates the regret into the utilities would do that. So we'd have to look at a particular regret-averse theory and then look to cases in which it and Buchak's theory come apart and see what we make of them. Buchak herself does offer an explicit argument in favour of her theory that goes beyond just appeal to the intuitive response to Allais. But it's quite involved and it might not have the same force.
On the second: thanks for the link!
On the third: I'm not so sure about the analogy with Zero. It's true that Sheila needn't defer to Zero's axiology, since we might think that which axiology is correct is a matter of fact and so Sheila might just think she's right and Zero is wrong. But risk attitudes aren't like that. They're not matters of fact, but something more like subjective preferences. But I can see that it is certainly a consistent moral view to be total hedonist utilitarian and think that you have no obligation to take the risk attitudes of others into account. I suppose I just think that it's not the correct moral view, even for someone whose axiology is total hedonist utilitarian. For them, that axiology should supply their utility function for moral decisions, but their risk attitudes should be supplied in the way suggested by the Risk Principle*. But I'm not clear how to adjudicate this.
Hi Richard, thanks for this post! Just a quick comment about your discussion of ex ante Pareto violations. You write:
That's not quite true. Even if all individuals have the same (non-neutral) risk attitude, we can get cases where everyone prefers one option to another even though it guarantees a worse outcome (and not just by the lights of total utilitarianism). See my paper "Rank-Weighted Utilitarianism and the Veil of Ignorance," section V.B.
Ah, thanks, Jake! That's really helpful! I'll make an edit now to highlight that.
Wow, what an interesting--and disturbing--paper!
My initial response is to think that it provides a powerful argument for why we should reject (Buchak's version of) risk-averse decision theory. A couple of quick clarificatory questions before getting to my main objection:
(1)
How do we distinguish risk-aversion from, say, assigning diminishing marginal value to pleasure? I know you previously stipulated that Sheila has the utility function of a hedonistic utilitarian, but I'm wondering if you can really stipulate that. If she really prefers the certainty of 49 hedons over a 50/50 chance of 100, then it seems to me that she doesn't really value 100 hedons as being more than twice as good (for her) as 49. Intuitively, that makes more sense to me than risk aversion per se.
(2)
Can you say a bit more about this? In particular, what's the barrier to aggregating attitude-adjusted individual utilities, such that harms to Bob count for more, and benefits to Bob count for less, yielding a greater total moral value to outcome A than to B? (As before, I guess I'm just really suspicious about how you're assigning utilities in these sorts of cases, and want the appropriate adjustments to be built into our axiology instead. Are there compelling objections to this alternative approach?)
(Main objection)
It sounds like the main motivation for REU is to "capture" the responses of apparently risk-averse people. But then it seems to me that your argument in this paper undercuts the claim that Buchak's model is adequate to this task. Because I'm pretty confident that if you go up to an ordinary person, and ask them, "Should we destroy the world in order to avoid a 1 in 10 million risk of a dystopian long-term future, on the assumption that the future is vastly more likely to be extremely wonderful?" they would think you are insane.
So why should we give any credibility whatsoever to this model of rational choice? If we want to capture ordinary sorts of risk aversion, there must be a better way to do so. (Maybe discounting low-probability events, and giving extra weight to "sure things", for example -- though that sure does just seem plainly irrational. A better approach, I suspect, would be something like Alejandro suggested in terms of properly accounting for the disutility of regret.)
Thanks for the comments, Richard!
On (1): the standard response here is that this won't work across the board because of something like the Allais preferences. In that case, there just isn't any way to assign utilities to the outcomes in such a way that ordering by expected utility gives you the Allais preferences. So, while the Sheila case is a simple way to illustrate the risk-averse phenomenon, it's much broader, and there are cases in which diminishing marginal utility of pleasure won't account for our intuitive responses.
On (2): it's possible you might do something like this, but it seems a strange thing to put into axiology. Why should benefits to Bob contribute less to the goodness of a situation just because of the risk attitudes he has?
On the main objection: I think you're probably right about the response many would have to this question, but that's also true if you ask them 'Should we do something that increases the probability of our billion-year existence by 1 in 10^14 rather than saving a million lives right now?' I think expected utility theory comes out as pretty unintuitive when we're thinking about longterm scenarios too. It's not just a problem for Buchak. And, in any case, the standard response by ordinary people might reflect the fact that they're not total hedonist utilitarians more than it does the fact that they are not Buchakians.
Thanks!
re: (1), can you point me to a good introductory reference on this? From a quick glance at the Allais paradox, it looks like the issue is that the implicit "certainty bias" isn't any consistent form of risk aversion either, but maybe more like an aversion to the distinctive disutility of regret when you know you otherwise could have won a sure thing? But maybe I just need to read more about these "broader" cases!
re: (2), the obvious motivation would be to avoid "overturning unanimous preferences"! It seems like a natural way to respect different people's attitudes to risk would be to allow them to choose (between fairly weighted options, that neither systematically advantage nor disadvantage them relative to others) how to weight potential costs vs benefits as applied to them personally.
On the main objection: sure, but traditional EU isn't motivated merely on grounds of being "intuitive". Insofar as that's the only thing going for REU, it seems that being counterintuitive is a much greater cost for REU specifically!
How so? The relevant axiological claim here is just that the worst dystopian futures are at least as bad as the best utopian futures are good. You don't have to be a total hedonist utilitarian (as indeed, I am not) in order to believe that.
I mean, do you really imagine people responding, "Sure, in principle it'd totally be worth destroying the world to prevent a 1 in 10 million risk of a sufficiently dystopian long-term future, if that future was truly as bad as the more-likely utopian alternative was good; but I just don't accept that evaluative claim that the principle is conditioned on here. A billion years of suffering for all humanity just isn't that bad!"
Seems dubious.
And, an admittedly more boring objection:
Maybe I'm unduly optimistic, but I have trouble wrapping my head around how lm could be even that likely. (E.g. it seems like suicide provides at least some protection against worst-case scenarios, unless we're somehow imagining such totalitarian control that the mistreated can't even kill themselves? But if such control is possible, why wouldn't the controllers just bliss out their subjects? The scenario makes no sense to me.)
How robust is the model's conclusions to large changes in the probability of lm (e.g. reducing its probability by 3 - 6 orders of magnitude)?
Yes, it's reasonably sensitive to this, though as you increase how risk averse you are, you also get extinction winning out even for lower and lower probabilities of lm. It's really a tradeoff between those two.
On your concerns about the probability of lm: I think people very often don't commit suicide even when their life falls below the level at which it's worth living. This might be because of optimism about the future, or connection to others and the feeling of obligation towards them, or because of an instinct for survival.