Weighted wellbeing population theory

Summary

The weighted wellbeing population theory suggests that first, negative wellbeing is eliminated with the |h|^5/2 prioritization weighting, then, overall wellbeing height is raised to the 0.9 threshold with the e^-10h prioritization weighting, and after, maximum wellbeing height is continuously raised. These weights have been developed by trial-error emotional reasoning under the veil of ignorance. This theory assumes that the wellbeing of a population can only increase, due to institutional effects. The depth of individuals’ sentience is considered alongside their wellness height. I discuss the applicability of the axiological desiderata presented by Greaves (2017) and debate further population theory considerations.

Wellbeing growth sequence

1. Weighted wellbeing population theory
2. Wellbeing height and depth visualizations
3. Visual analog scale wellbeing data gathering method

Theory with values discussion

Considering that momentary wellbeing of an individual, mw_i, is calculated as the product of that individual’s momentary wellbeing height, h_i, and depth of perception, d_i:

I suggest that

1. Negative wellbeing is eliminated with |h|^5/2 prioritization weighting, then
2. 0.9 wellbeing height threshold is met with e^-10h prioritization weighting, then
3. Maximum wellbeing height is continuously raised.

This theory assumes that the wellbeing of a population can only increase, due to institutional effects. Either, an institution continuously improves the wellbeing of a population or it leaves it constant. In the latter case an institutional improvement can be implemented to raise a population’s wellbeing. This model suggests that institutions that would deteriorate populations’ wellbeing do not exist and wellbeing-reducing institutional changes do not occur.

These prioritization weights and the threshold value have been found by trial-error emotional reasoning under the veil of ignorance. I have been graphing different curves and imagining a 0.1 wellbeing height increase at a few places alongside these curves. Visually, I have been comparing the areas under a derivative curve (and then integrated it and dropped the constants to get the weighing curve) and calculating how many times an improvement would be weighed more heavily than another one substituting values into the integrated function. I selected the curves where I felt that this would be overall approved under the veil of ignorance and thus perceived as fair. An analogy can be someone at the doctor seeing that they are prioritized or deprioritized according to an equation: if everyone approves it, then the equation is used. A shortcut to reason about this is imagining oneself with variously troubling issues and having scarce resources to maximize their improvement. I am suggesting that if the improvement of 1/62 of one’s wellbeing from -0.9 to -0.8 required the same resources as an improvement of 61/62 of one's wellbeing from -0.1 to 0.1, people would be just indecisive. However, I can imagine that a prioritization equation should be more complicated than this, so I am interested in a better under the veil of ignorance approved weighting function.

1) Eliminate negative wellbeing with the |h|^5/2 prioritization weighting

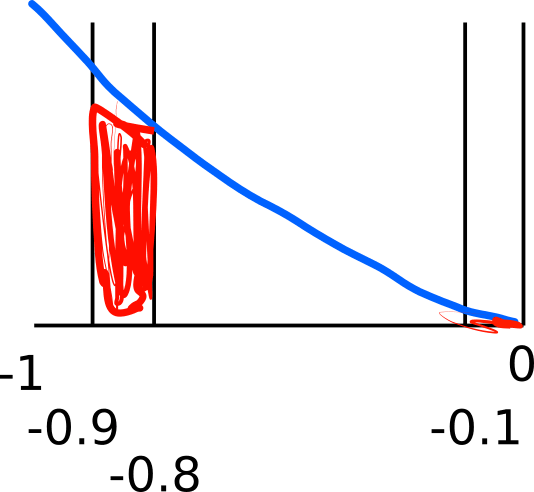
To eliminate negative wellbeing with equal consideration to all individuals, I suggest using the |h|^5/2 prioritization weighting. With this weighting, for example, reducing suffering from -0.9 to -0.8 is about 62× as valuable as reducing negative wellbeing from -0.1 to 0.¹ This can be visualized by comparing the two red areas under the |h|^3/2 curve.²

2) Raise overall wellbeing height to the 0.9 threshold with the e^-10h prioritization weighting

After negative wellbeing is eliminated, welfare should be increased to the 0.9 threshold, using the e^-10h weighting. Improving wellness by an additional 0.1 increment is always e× as valuable as improving wellness by an amount without such increment. For example, increasing welfare from  0.1 to 0.2 is e× as valuable as changing such from 0 to 0.1.³ Or, raising wellness from 0.4 to 0.5 is about 55× valuable as increasing wellbeing from 0 to 0.1.⁴ This can be visualized as the comparison of areas under the e^-10h curve.⁵ Also this weighing can be universally considerate.

3) Continuously raise the maximum wellbeing height

With high universal wellbeing, the maximum height can be continuously raised. A raised threshold will move some individuals below the 0.9 value. These persons’ wellbeing should be raised with the weighting suggested by this theory. The infinite continuation of this system should be prioritized over temporary raises of maximum wellness. Further sentience should be continuously sought on earth and in the universe in a manner that does not present a risk to the framework. Thus, the long-term wellness of all sentient beings should be secured and an emergence of a system that seeks other objective than universal wellbeing prevented.

Axiological discussion

This discussion is based on Population axiology (Greaves, 2017).

Repugnant conclusion

The repugnant conclusion does not apply since a high wellness threshold is used. By definition, a weak repugnant conclusion (pp. 9–10) occurs when a threshold is used. However, one may argue that using a high threshold, such as 90% of the maximum wellness that any individual has ever experienced, and continuously raising such threshold may be acceptable.

Sadistic conclusion

The sadistic conclusion is prevented by eliminating negative wellness before positive wellbeing is increased.

The mere addition principle

The mere addition principle does not apply under or above the wellness height threshold. The wellbeing of additional people whose welfare is below the threshold is raised above such critical level before maximum wellness is increased. The wellbeing of additional people above the threshold can be assumed comparable to that of any other persons whose welfare is above that level.

Variable value theory

Since individual consideration is independent of the number of already existing individuals, variable value theory principles do not apply.

Geometrism

Geometrism does not apply since individuals are considered independently of their order in a positive or negative wellbeing sequence. Further, the wellness of negative and positive wellbeing experiencing groups is not summed. However, since worse suffering is weighted more heavily, the calculation for individuals experiencing negative wellness is similar to that of the negative term of the geometrist axiology equation (p. 7). Positive wellness below the threshold is weighted more, not less, heavily, with decreasing wellbeing. Therefore, the positive term of the geometrist axiology equation does not function similarly as positive wellness weighting under the threshold. Wellness above the critical level is not weighted, thus, geometrism does not apply above such level.

Non-anti-egalitarianism

This theory is consistent with non-anti-egalitarianism. Since the derivative of both positive and negative weighting equation is convex, less extreme suffering, even if that is outweighed by the same linear increase in wellbeing, as well as well as less below-threshold positive wellbeing, even if that outweighed by the same linear increase in wellness, is preferred over vice versa situations.

Critical level theories

Since this theory uses a threshold, it can be broadly understood as a critical level theory. However, due to the prioritization of negative wellness elimination, the use of a threshold does not imply the sadistic conclusion.

Neutrality principle

The neutrality principle applies above the critical level and to positive wellness when suffering exists but does not apply to additional negative wellness or to additional positive wellbeing below the threshold if wellness below that threshold already exists.

The principle of equal existence

The principle of equal existence does not apply since the wellness level of additional persons is considered.

Non-impartial theories

This theory is impartial because it considers all individuals across times as well as persons whose future existence is uncertain.

Harm-minimisation theories

Since this theory considers the real, rather than the potential, wellness of individuals below the wellness threshold and does not differentiate wellbeing heights above the critical level, it does not use the harm-minimisation principle at any point in time. However, since the maximum wellness is continuously increased when overall wellness is above the threshold, wellbeing potential is developed.

Theories with widespread incomparability

Since this theory addresses populations with different numbers of individuals by the same principle, the widespread incomparability principle does not apply.

Impossibility theorems

I suggest that a theory that considers continuous improvement, prioritizes negative wellbeing elimination, and uses a high wellness threshold satisfies the axiological desiderata summarized by Greaves. In addition, by using wellbeing height and depth weighting, I suggest an efficient and impartial way of increasing wellness.

Further discussion

Utility monsters

This theory addresses the utility monster problem by aiming for a framework endorsed by all, regardless of their relative wellness depth. For example, if a greatly suffering utility monster is discovered in the future, its wellbeing should be raised above the threshold. Or, if a utility monster exists right below the threshold, it may be still worth improving their wellness above such level, forgoing the opportunity to improve the wellbeing of other individuals whose lives are barely worth living. For example, consider that such monster is billions of copies of a single individual. Perhaps, improving their wellness should be prioritized over raising the wellbeing of millions⁶ of the same wellness depth individuals by the same unweighted value.

Yet, one may avoid this discussion by allowing any individual, including a utility monster, to forgo further positive wellness improvement in order to prioritize such for other individuals. In addition, suffering individuals, including those with extensive wellbeing depth, who do not effect greater weighted wellness improvement, should be allowed to stop existing.

Practical impossibility

One may argue that achieving a very high universal wellness is impossible. It can be also argued that with technological advancements, wellness study, and institutional development, this may be possible.

Existential threat

It can be asserted that this theory presents an existential threat to different populations, such as those which are suffering or experiencing relatively low wellness. This is the objective of this framework: populations that are suffering or experiencing below-threshold wellness should eventually not exist. However, populations should not be defined by species, but rather by identities, that the individuals would change for higher wellness ones. In addition, since high wellness must be sustained (considering the risk of the emergence of an even more suffering system with worse population axiology), an infinitely sustainable number of individuals who can keep increasing overall wellbeing must always exist. Thus, this framework presents an existential threat only to identities that can experience higher wellness in the long term.

Universality

This framework only considers sentient experiences and enables the achievement of any objectives.

Footnotes

¹ (0.9^2.5-0.8^2.5)/(0.1^2.5-0^2.5) ≈ 62 

² d/dh |h|^5/2=5/2h|h|^1/2. For all negative h and omitting the constants, =|h|^3/2.

³ (e⁰-e^-1)/(e^-1-e^-2) = e

⁴ (e⁰-e^-1)/(e^-4-e^-5) ≈ 55

⁵ d/dh e^-10h = -10e^-10h. Omitting the constant, =e^-10h.

⁶ (e⁰-e^-1)/(e^-8-e^-9) ≈ 2981