Bayes' Theorem
Bayes' Theorem (also known as Bayes' Rule or Bayes' Law) is a law of probability that describes the proper way to incorporate new evidence into prior probabilities to form an updated probability estimate. It is commonly regarded as the foundation of consistent rational reasoning under uncertainty. Bayes' Theorem is named after Reverend Thomas Bayes, who proved the theorem in 1763.
See also: Bayesian probability, Priors, Likelihood ratio, Belief update, Probability and statistics, Epistemology, Bayesianism
Bayes' theorem commonly takes the form:
where A is the proposition of interest, B is the observed evidence, P(A) and P(B) are prior probabilities, and P(A|B) is the posterior probability of A.
With the posterior odds, the prior odds and the likelihood ratio written explicitly, the theorem reads:
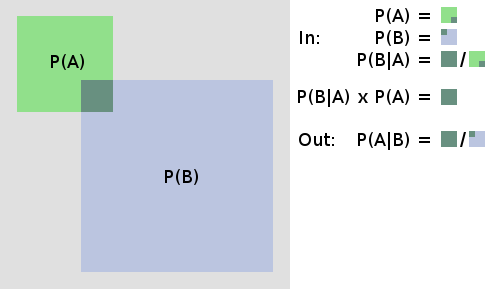
Visualization of Bayes' Rule
External links
- Arbital Guide to Bayes' Rule
- An Intuitive Explanation of Bayes' Theorem by Eliezer Yudkowsky
- Visualizing Bayes' theorem by Oscar Bonilla
- Using Venn pies to illustrate Bayes' theorem by oracleaide
- A Guide to Bayes’ Theorem – A few links by Alexander Kruel
- Bayes' Theorem, Wikipedia
- Joyce, James. 2003. Bayes’ theorem. In Edward Zalta (ed.), Stanford Encyclopedia of Philosophy.
- Wikipedia. 2016a. Base rate fallacy.
- Wikipedia. 2016b. False positive paradox.
