Vasco Grilo🔸
Bio
Participation4
I am a generalist quantitative researcher. I am open to volunteering and paid work. I welcome suggestions for posts. You can give me feedback here (anonymously or not).
How others can help me
I am open to volunteering and paid work (I usually ask for 20 $/h). I welcome suggestions for posts. You can give me feedback here (anonymously or not).
How I can help others
I can help with career advice, prioritisation, and quantitative analyses.
Posts 223
Comments2781
Topic contributions40
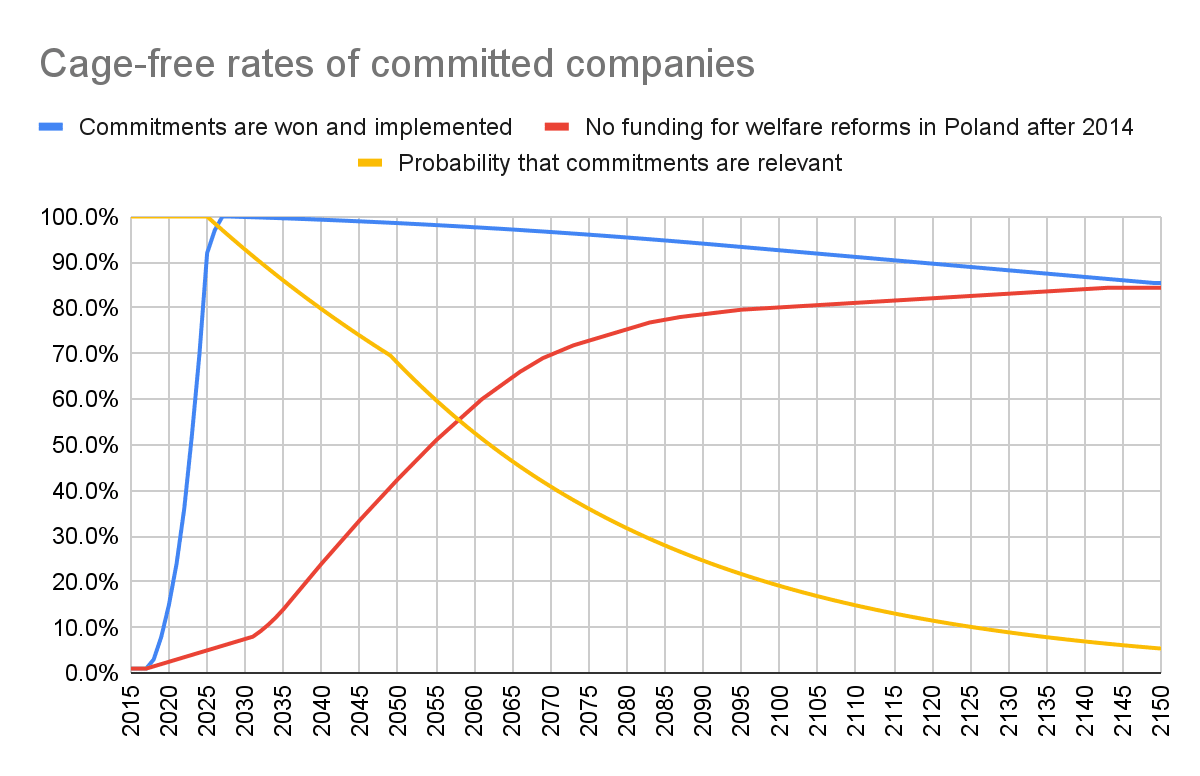
Hi Saulius.
I tried estimating years of impact using graphs like this:
[...]
The yellow line accounts for the possibility that commitments will stop being relevant due to things like x-risks, global catastrophic risks, societal collapse, cultured meat taking over, animals bred not to suffer, black swans, etc. [...]
[...]
Finally, we estimate the expected proportion of hens used by companies that will be cage-free each year as follows: (blue - red) ✕ yellow. And then we add up the result for all years to calculate years of impact.
I would estimate the number of layer-years improved in expectation in year Y from "expected population of layers in year Y"*("expected population of layers in cages in year Y without the intervention as a fraction of all of them in year Y" - "expected population of layers in cages in year Y with the intervention as a fraction of all of them in year Y") = P(Y)*(f_control(Y) - f_intervention(Y)), which is correct by definition. I would then calculate the total number of layer-years improved adding the effects from the year in which the intervention started on. I believe the annual effects should eventually go to 0, such that there is no need to add the effects of all the years until infinity. It is enough to consider the years accounting for the vast majority of the total number of layer-years improved.
P, f_control, and f_intervention relate to your yellow, red, and blue lines, but their meaning is more intuitive. In addition, the yellow line in your formula should not be strictly seen as a probability for it to work in all cases. A probability describes effects that would make the fraction of hens in cages the same with and without the intervention, which applies to, for example, human extinction. However, there are non-binary gradual effects like the raise of alternative proteins which make the fraction of hens in cages with and without the intervention more similar in expectation, but without all the effect coming from the possibility of the fraction with and without the intervention becoming the same.
I think the post The Selfish Machine by Maarten Boudry is relevant to this discussion.
Consider dogs. Canine evolution under human domestication satisfies Lewontin’s three criteria: variation, heritability, and differential reproduction. But most dogs are bred to be meek and friendly, the very opposite of selfishness. Breeders ruthlessly select against aggression, and any dog attacking a human usually faces severe fitness consequences—it is put down, or at least not allowed to procreate. In the evolution of dogs, humans call the shots, not nature. Some breeds, like pit bulls or Rottweilers, are of course selected for aggression (to other animals, not to its guardian), but that just goes to show that domesticated evolution depends on breeders’ desires.
How can we extend this difference between blind evolution and domestication to the domain of AI? In biology, the defining criterion of domestication is control over reproduction. If humans control an animal’s reproduction, deciding who gets to mate with whom, then it’s domesticated. If animals escape and regain their autonomy, they’re feral. By that criterion, house cats are only partly domesticated, as most moggies roam about unsupervised and choose their own mates, outside of human control. If you apply this framework to AIs, it should be clear that AI systems are still very much in a state of domestication. Selection pressures come from human designers, programmers, consumers, and regulators, not from blind forces. It is true that some AI systems self-improve without direct human supervision, but humans still decide which AIs are developed and released. GPT-4 isn’t autonomously spawning GPT-5 after competing in the wild with different LLMs; humans control its evolution.
By and large, current selective pressures for AI are the opposite of selfishness. We want friendly, cooperative AIs that don’t harm users or produce offensive content. If chatbots engage in dangerous behavior, like encouraging suicide or enticing journalists to leave their spouse, companies will frantically try to update their models and stamp out the unwanted behavior. In fact, some language models have become so safe, avoiding any sensitive topics or giving anodyne answers, that consumers now complain they are boring. And Google became a laughing stock when its image generator proved to be so politically correct as to produce ethnically diverse Vikings or founding fathers.
Thanks for clarifying, Erich. I believe Falk was referring to Yudkowsky and Soares. I have not read their book. I have just listened to podcasts they have done, and skimmed some of their writings. However, I think the broader point stands that they often use language that implies much greater confidence in and robustness of the possibility of human extinction than warranted by their arguments.
Hi Tom.
From a longtermist (~totalist classical utilitarian) perspective, there's a huge difference between ~99% and 100% of the population dying, if humanity recovers in the former case, but not the latter. Just looking at GCRs on their own mostly misses this nuance.
I would be curious to know your thougths on my post arguing that decreasing the risk of human extinction is not astronomically cost-effective.
From a longtermist (~totalist classical utilitarian) perspective, preventing a GCR doesn't differentiate between "humanity prevents GCRs and realises 1% of it's potential" and "humanity prevents GCRs realises 99% of its potential"
The same applies to preventing human extinction over a given period. Humans could go extinct just after the period, or go on to an astronomically valuable, and I believe the former is much more likely.
From a longtermist (~suffering focused) perspective, reducing GCRs might be net-negative if the future is (in expectation) net-negative
This also applies to reducing the risk of human extinction.
Thanks for sharing, Peter! Have you considered making the doc available for reading even if people do not make a copy? I wonder whether a few people would only check it this way, even though a copy can easily be deleted.
Here are some links shared in the doc which many may find useful regardless of whether they do quarterly reviews, although you note "the point is to do a review and plan!".
Appendix A: Get Inspired
Read…
- The 5-Step Process to Get What You Want Out of Life
- Humans are not automatically strategic
- How to be successful
- How to work hard
- There is no speed limit
- If you want to follow your dreams, you have to say no to all the alternatives
- Staring into the abyss
- You and your research
- The work-rest fractal
- Notes and Reflections on “Deep Work” by Cal Newport
- Notes on "A World Without Email", plus my practical implementation
- High density fun
- The Fifteen Commitments of Conscious Leadership
- List of my Favorite Named Adages, Aphorisms, Dictums, Laws, Maxims, and Rules to Live By
Though remember not to get too distracted here! Just read enough to get inspired and then stop. The point is to do a review and plan!
There is currently not any intervention which robustly increases welfare in expectation due to potentially dominant uncertain effects on soil animals and microorganisms. More research on how to compare welfare across species is needed to figure out whether these matter.
I see. I guess the probability over the next 10 years of something like what I described is lower than 0.001 %. I remain open to bets against short AI timelines, or what they supposedly imply, up to 10 k$. Do you see any that we could make that is good for both of us considering we could invest our money, and that you could take loans?

I completely agree with what you just stated (although I have not read the post you linked), but I do not understand why it would undermine the broader point I mentioned in my comment.