Moloch is a poetic way of describing failures of coordination and coherence inside an agent or between agents and the generation of harmful subcomponents or harmful agents. Perhaps this could be decomposed further, or at least partially covered, by randomly generated accidents, Goodhart’s law failures, and conflicts of optimization. Let’s zoom in on one aspect, conflicts of optimization.
What are conflicts of optimization? They are situations where more than one criterion is being optimized for and in practice improving one criterion causes at least one other criterion to become less optimal.
When does this occur? It occurs when you cannot find a way to improve all optimization criteria at the same time. For instance, if you cannot produce both more swords and more shields because you only have a limited amount of iron then you have a conflict of optimization.
This can be described by the concept of Pareto optimality. If you’re at a Pareto optimal point then there is no way to improve all criteria and the set of all such points is called the Pareto frontier.
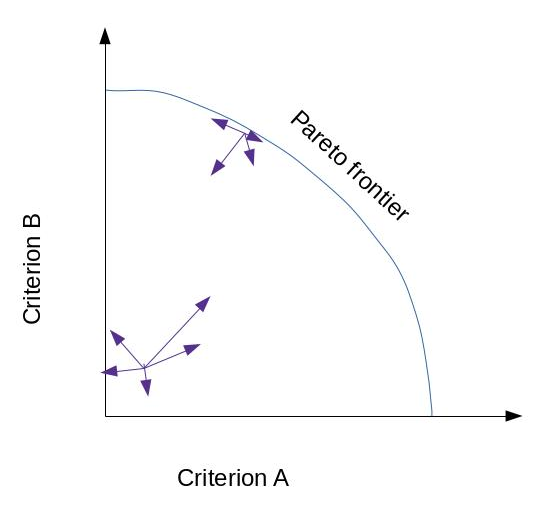
What this looks like is that if you’re near or on the Pareto frontier there are few to zero ways to improve all criteria and as you get further away there are more options for improving all criteria. Iteratively then you can imagine that around every point there are some known ways to move that may be visualized as vectors from that point. A sequence of such changes is then a sequence of movements along vectors. Generally what you’d expect (with caveats) is that the trajectory moves up and to the right until it hits the pareto optimal frontier and then skates along the frontier till one or the other optimization process wins or they are at equilibrium (relatedly).
An example of this dynamic is job negotiations done well. At first both parties are working towards finding changes that benefit them both but as time goes on such opportunities run out and the last parts of the negotiation proceed in a zero sum way (like perhaps salary).
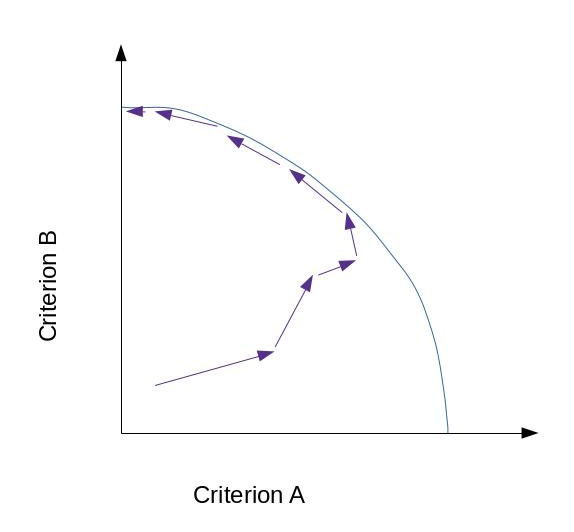
In practice the Pareto frontier isn’t necessarily static because background variables may be changing in time. As long as the process of moving towards the frontier is much faster than the speed at which the frontier changes though we’d continue to expect again the motion of going towards the frontier and then skating along it.
Between the criteria this then translates essentially to a bunch of positive sum transformations far away from the Pareto frontier and then as you get closer to it transformations become less and less positive sum, until finally becoming zero sum (one can only win at the expense of the other losing). This has natural implications about how game theory actors relate as progress occurs when going towards a Pareto frontier.
Let’s now relate this to Moloch. Let the x axis be optimizing for humanity’s ultimate values, the y axis be optimizing for competitiveness (things like winning in politics, wars, persuasion, and profit making), the points represent the world’s state in terms of x and y, and the trajectory through the points be how the world develops. Given the above we’d expect that at first competitiveness and the accomplishment of humanity’s ultimate values are both improved but eventually they come apart and the trajectory skates along the Pareto frontier (that roughly speaking happens when we are at maximum technology or technological change becomes sufficiently slow) until it maximizes competitiveness.
This is one of Moloch’s tools: The movement towards competitive advantage over achieving humanity’s ultimate values because the set of transformations is constrained near the Pareto frontier.

I like the first bit, but am a bit confused on the Moloch bit. Why exactly would we expect that it "maximizes competitiveness"?
The reason why we'd expect it to maximize competitiveness is in the sense that: what spreads spreads, what lives lives, what is able to grow grows, what is stable is stable... and not all of this is aligned with humanity's ultimate values; the methods that sometimes maximize competitiveness (like not internalizing external costs, wiping out competitors, all work and no play) much of the time don't maximize achieving our values. What is competitive in this sense is however dependent on the circumstances and hopefully we can align it better. I hope this clarifies.
I think I had the same thought as Ozzie, if I'm interpreting his comment correctly. My thought was that this all seems to make sense, but that, from the model itself, I expected the second last sentence to be something like:
And then that'd seem to lead to a suggestion like "Therefore, if the world is at this Pareto frontier or expected to reach it, a key task altruists should work on may be figuring out ways to either expand the frontier or increase the chances that, upon reaching it, we skate towards what we value rather than towards competitiveness."
That is, I don't see how the model itself indicates that, upon reaching the frontier, we'll necessarily move towards greater competitiveness, rather than towards humanity's values. Is that idea based on other considerations from outside of the model? E.g., that self-interest seems more common than altruism, or something like Robin Hanson's suggestion that evolutionary pressures will tend to favour maximum competitiveness (think I heard Hanson discuss that on a podcast, but here's a somewhat relevant post).
(And I think your reply is mainly highlighting that, at the frontier, there'd be a tradeoff between competitiveness and humanity's values, right? Rather than giving a reason why the competitiveness option would necessarily be favoured when we do face that tradeoff?)
Yes, the model in itself doesn't say that we'll tend towards competitiveness. That comes from the definition of competitiveness I'm using here and is similar to Robin Hanson's suggestion. "Competitiveness" as used here just refers to the statistical tendency of systems to evolve in certain ways - it's similar to the statement that entropy tends to increase. Some of those ways are aligned with our values and others are not. In making the axes orthogonal I was using the, probably true, assumption that most ways of system evolution are not in alignment with our values.
(With the reply I was trying to point in the direction of this increasing entropy like definition.)
I like this model but I think a more interesting example can be made with different variables.
Imagine x and y are actually both good things. You could then claim that a common pattern is for people to be pushing back and forth between x and y. But meanwhile, we may not be at the Frontier at all if you add z. So let's work on z instead!
In that sense, maybe we are never truly at the frontier, all variables considered.
Related to this line of thinking: affordance widths
Your comment also reminded me of Robin Hanson's idea that policy debates are typically like tug of war between just two positions, in which case it may be best to "pull the rope sideways". Hanson writes: "Few will bother to resist such pulls, and since few will have considered such moves, you have a much better chance of identifying a move that improves policy."
That seems very similar to the idea that we may be at (or close to) the Pareto frontier when we consider only two dimensions, but not when we add a third, so it may be best to move towards the three-dimensional frontier rather than skating along the two-dimensional frontier.
Nice! I would argue though that because we do not consider all dimensions at once generally speaking and because not all game theory situations ("games") lend themselves to this dimensional expansion we may, for all practical purposes, sometime find ourselves in this situation.
Overall though, the idea of expanding the dimensionality does point towards one way to remove this dynamic.
For a model of how conflicts of optimization (especially between agents pursuing distinct criteria) may evolve when the resource pie grows (i.e. when the Pareto frontier moves away from the origin), see Paretotopian Goal Alignment (Eric Drexler, 2019).
There can be a common interest for all parties to expand the Pareto frontier, since it expands the opportunities of everyone scoring better at the same time on their respective criteria.
This seems approximately right. I have some questions around how competitive pressures relate to common-good pressures. It's sometimes the case that they are aligned (e.g. in many markets).
Also, there may be a landscape of coalitions (which are formed via competitive pressures), and some of these may be more aligned with the common good and some may be less. And their alignment with the public good may be orthogonal to their competitiveness / fitness.
It would be weird if it were completely orthogonal, but I would expect it to naturally be somewhat orthogonal.
I agree with your thoughts. Competitiveness isn't necessarily fully orthogonal to common good pressures but there generally is a large component that is, especially in tough cases.
If they are not orthogonal then they may reach some sort of equilibrium that does maximize competitiveness without decreasing common good to zero. However, in a higher dimensional version of this it becomes more likely that they are mostly orthogonal (apriori, more things are orthogonal in higher dimensional spaces) and if what is competitive can sorta change with time walking through dimensions (for instance moving in dimension 4 then 7 then 2 then...) and iteratively shifting (this is hard to express and still a bit vague in my mind) then competitiveness and common good may become more orthogonal with time.
The Moloch and Pareto optimal frontier idea is probably extendable to deal with frontier movement, dealing with non-orthogonal dimensions, deconfounding dimensions, expanding or restricting dimensionality, and allowing transformations to iteratively "leak" into additional dimensions and change the degree of "orthogonality."
Overall I think this is pretty good!
Two comments:
1) It might be useful to imagine that since we're bounded-rational and have imperfect information, that in many cases we don't know where the frontier is, or we don't know our orientation and are uncertain about which actions lead to a world we care about.
2) Since it's easier to optimize for certain things like profit rather than value, certain movements on the board might be easier, meaning we will trend in the direction of those shifts.