A response to Puzzles for Everyone. 

Richard Yetter Chappell argues that problems in decision theory and population ethics are not just puzzles for utilitarians, but puzzles for everyone. I disagree. I think that the puzzles Richard raises are problems for people tempted by very formal theories of morality and action, which come with a host of auxiliary assumptions one may wish to reject.

Decision Theory

Richard’s post cites two examples: one from decision theory, and one from population ethics. 

To support his decision-theoretic case, Richard references this paper, in which you’re faced with the following payoff table:

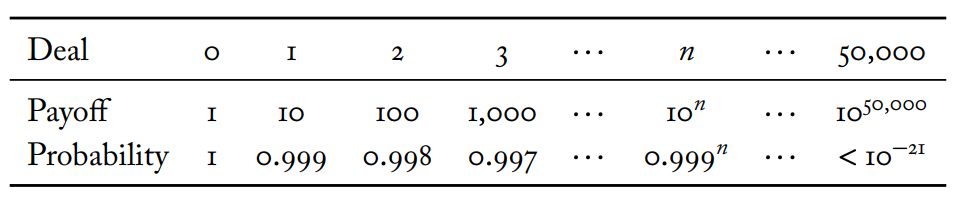
The case is nicely summarized by Tomi Francis: 

“You have one year left to live, but you can swap your year of life for a ticket that will, with probability 0.999, give you ten years of life, but which will otherwise kill you immediately with probability 0.001. You can also take multiple tickets: two tickets will give a probability 0.9992 of getting 100 years of life, otherwise death, three tickets will give a probability 0.9993 of getting 1000 years of life, otherwise death, and so on. It seems objectionably timid to say that taking n+1 tickets is not better than taking n tickets. Given that we don’t want to be timid, we should say that taking one ticket is better than taking none; two is better than one; three is better than two; and so on.” 

Sure, fine, we don’t want to be timid. 

… But, if we’re not timid, the end-point of this series of decisions looks objectionably reckless. If you act in line with a non-timid decision procedure telling you to take each ticket, you end up in a situation where you’re taking (potentially arbitrarily unlikely) moonshot bets for astronomically high payoffs. In their paper, Beckstead and Thomas argue that, alas, we’re caught in a bind — any possible theory for dealing with uncertain prospects will be one of: timid, reckless, or intransitive. 

1.1.

In many ways I’m sympathetic to the motivations behind Chappell's post, because I’ve encountered a lot of unfair derision of others who sincerely attempt to deal with problematic implications of their values. And, often, the sources of mockery do appear to come from people who “haven’t actually thought through any sort of systematic alternative” to the people they're deriding. 

Still, I think his post is wrong. So what do I actually do in a situation like this?

I’ll get to that. But first, I want to discuss some basic setup required for Beckstead and Thomas’ paper. While Beckstead and Thomas’ paper doesn’t explicitly rely on expected utility theory (EUT), I think their conception of deontic theory (i.e., the theory of right action) shares the following structure with EUT: we begin with an agent with some ends $E$(represented by some numerical quantity), a decision-context $D$ (represented by a subjective probability distribution over some exogenously given state space). 

Now, back to the gamble. What would I actually do in that situation? In practice, I think I’d probably decide to take actions via the following decision-procedure:

STOCHASTIC: Decide whether to take the next bet via a stochastic decision procedure, where you defer your decision to take each successive bet to some procedure which outputs Take with probability p, and Decline with probability (1-p), for some 0 < p < 1. 

So, for each bet, I defer to some random process. For simplicity, let's say I draw from an urn with $p\%$ black balls, in which I take Ticket 1 if I draw a black ball, and decline otherwise. If the ball is black, I iterate the process, until I draw a non-black ball. If I draw $n$black balls, I take $n$ tickets. This process, STOCHASTIC, determines the number of tickets I will take. 

I look at this strategy, and it seems nice. It's a bit clunky, but I was interested in decision theory because it offered a particular promise — the promise of a framework telling agents how to do better by their own values. And, here, I feel as though STOCHASTIC serves my ends better than alternatives I can imagine. Thus, absent some convincing argument telling me that this decision-procedure leads my awry in some way I’m unaware of, I’m happy to stick with it. I have my ends. And, relative to my ends, I endorse STOCHASTIC in this decision-context. It strikes, for me, an appropriate balance of risk and reward. 

1.2.

Of course, if you insist on viewing each action I take as expressing my attitude towards expected consequences, then my actions won’t make sense. If I accepted gamble $n$, why would I now refuse gamble $n+1$? After all, gamble $n+1$ is just the same gamble, but strictly better.  

But, well, you don’t have to interpret my actions as expressing attitudes towards expected payoffs. I mean this literally. You can just … not do that. Admittedly, I grant that my performing any action whatsoever could, in principle, be used to generate some (probability function, utility function) weighting which recovers my choice behavior. But I don’t see that anyone has established that whatever $p(.)U(.)$ weighting you use to represent my behavior contains the probability function that I must use to guide my behavior going forward. I don’t think you get that from Dutch Book arguments, and I don’t think you get it from representation theorems.

You may still say that deferring to a randomization process to determine my actions looks weird — but it’s a weird situation! I don't find it all that puzzling to believe, when confronted with a weird situation, that the best thing to do looks a little weird. STOCHASTIC is a maxim telling me how to behave in a weird situation. And, given that I'm in an unusual decision-context, deferring to an unusual decision-procedures doesn't feel all that counter-intuitive. I don’t have to refer back to a formal theory which tells me what to do, but rather refer back to the reasons I have for performing actions in this particular decision-context, given my ends. And, at bottom, my reasons for acting in this way include a desire for life-years, and some amount of risk-aversion. I don’t see why I’m required to treat every local action I take as expressing my attitude towards expected consequences, when this decision-procedure does globally worse by my ends.  

If you prefer some alternative maxim for decision-making, then, well, good for you. Life takes all sorts. But if you do prefer some other procedure for decision-making, then I don’t really think Beckstead and Thomas’ paper is really a puzzle for you, either.^[1] Either you’re genuinely happy with recklessness (or timidity), or else you have antecedent commitments to the methodology of decision theory — such as, for example, a commitment to viewing every action you take as expressing your attitude to expected consequences. But I take it (per Chappell) that this was meant to be a puzzle for everyone, and most people don’t share that commitment — I don’t even think those who endorse utilitarian axiologies need that commitment! 

1.3.

If you’re committed to a theory which views actions as expressing attitudes towards expected consequences, then this is a puzzle for you. But I’m not yet convinced, from my reading of the decision-theoretic puzzles presented, that these puzzles are puzzles for me. Onto ethics.

Population Ethics

When discussing population ethics, Chappell intimates at the complicated discussions surrounding Arrhenius’ impossibility proof for welfarist axiologies. 

Chappell's post primarily responds to a view offered by Setiya, and focuses on the implications of a principle called ‘neutrality’. That said, I interpret Richard to be making a more general point: we know, from the literature in population axiology, that any consistent welfarist axiology has to bite some bullet. Setiya (so claims Chappell) can’t avoid the puzzles, for any plausible moral theory has some role for welfare, and impossibility theorems are problems for all such theories.

Chappell is right to say that the puzzles of population axiology are not just puzzles for utilitarians, but rather (now speaking in the authorial voice) puzzles for theorists who admit well-defined, globally applicable notions of intrinsic utility. I certainly think that some worlds are better than others, and I also believe that there are contexts under which it makes sense to say that some population has higher overall welfare than another. But I’m not committed (and nor do I see strong arguments for being committed) to the existence of a well-defined, context-independent, and impartial aggregate welfare ranking.   

2.1.

Parfit is the originator of the field of population ethics. One of his famous cases is the Mere Addition Paradox. It starts with the bars below, and proceeds through argumentative steps well summarized on Wikipedia. We’ll recount it briefly here, but feel free to skip to 2.2 if you already know the deal.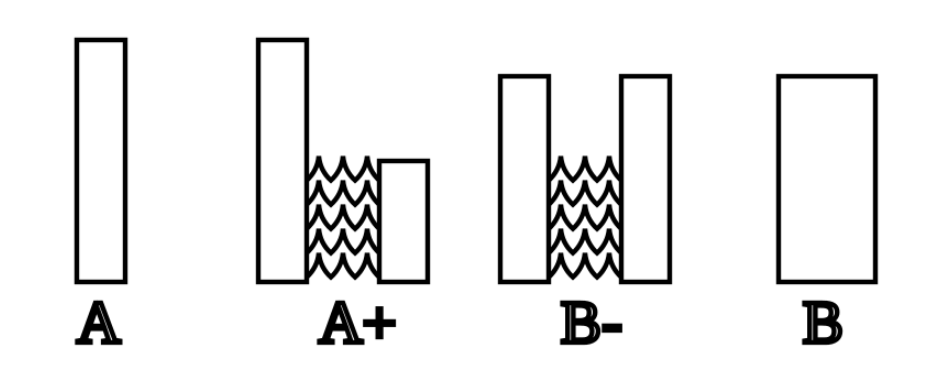

Start with World A, full of loads and loads (let’s say 10 billion) of super happy people. Then, someone comes along and offers to create a disconnected world full of merely very happy people. They’re happier than anyone alive today, but still far short of the super happy people. But no one has any resentment, and the worlds don’t interact. A+, we may think, is surely no worse than A. We’ve simply added a bunch of people supremely grateful to be alive.

Now someone comes along and says: “hey, how about we shift from A+ to B-”, where B- has higher total welfare, and also higher average welfare. You don’t actively hate equality, so it seems that B- is better than A+. Then, we merge the groups in B- to a single group in B. That’s surely no worse. So B > A. 

You iterate these steps. We end up with some much larger world, Z, full of people with lives that are worth living, but only just. If you endorsed all the previous steps, it seems that Z > A. That is, there’s some astronomically large population, Z, full of lives that are barely worth living — arrived at through a series of seemingly plausible steps — that you have to say is better than Utopia. Lots of people don’t like this, hence the name: the repugnant conclusion.

2.2.      

I have two qualms with the basic setup. First, I’m not convinced that you can universaly make these small, iterative differences to aggregate welfare levels in a way that gets you to the repugnant conclusion, because I’m not convinced that I’m committed to a concept of aggregate welfare which has a propety Arrhenius calls finite fine-grainedness. That is, the incremental steps in the Mere Addition Paradox (like the move from A+ to B) assume that it's always possible to make slight, incremental changes to aggregate welfare levels.

Second, even if I were committed to a (universally applicable) concept of aggregate welfare, Parfit’s initial presentation put forth bars of varying widths and heights, which are supposed to correspond to some set of creatures with valenced experiential states. I care about these creatures, and their experiences. However, in order to derive any practical conclusion from the bars of varying widths and heights, I need to have some idea of what mapping I’m meant to have between imaginable societies and the aforementioned bars of varying widths and heights.

I’ve not yet encountered someone who can show me, relative to a mapping between societies and bars (numbers, whatever) that I find plausible, that I’m in fact committed to some counterintuitive consequence which is meant to beset every plausible normative theory. I simply have judgments about the ranking of various concretely described worlds, and (largely implicit) decision procedures for what to do when presented with the choice of various worlds. The axioms required for various impossibility proofs assume that I already possess a global aggregate welfare ranking, defined in every context, and present various axioms which are meant to apply to this global welfare ranking. I'm much more inclined to think that models under which assume an impartial aggregate welfare ordering are useful in some contexts, but find myself unpersuaded that the assumption of an impartial aggregate welfare ordering is anything more than a convenient modeling assumption.

My conception of ethics is admittedly unsystematic, but I don’t see that as a failing by itself. I see the virtues in coherency, for — if I’m not coherent — then I don’t take myself to be saying anything at all about what I take to be better or worse. But, currently, I think that I am coherent. You can show that people are incoherent when you can show that they are jointly committed to two principles which are collectively inconsistent. And, I think, you can show that people have implicit commitments by showing that something follows from one of their more explicit commitments, or from showing that they engage in an activity which can only be justified if they endorse some other commitment. But, as far as I’m aware, no one has shown me that. 

If someone shows me that I’m incoherent, I’ll reconsider my principles. But, absent arguments showing me that I am committed to the principles required to get population ethics off the ground, I remain happy in claiming that Chappell poses puzzles for some, but not for me.

1. ^{^}

   Thanks to Richard for nudging me to say something about whether I avoid the puzzles, rather than just constructing a solution I personally find satisfying.