LW crosspost

This is the script of Rational Animations' video linked above. It's about how to take over the universe with amounts of energy and resources that are small compared to what is at our disposal in the Solar System. It's based on this paper, by Anders Sandberg and Stuart Armstrong. 

This is our highest-quality video so far. Below, the script of the video.

Let’s take over the universe in three easy steps

Welcome. We’ve heard that you want to take over the universe. Well, you’ve come to the right place. In this video, we’ll show you how to reach as many as four billion galaxies with just a few relatively easy steps and six hours of the Sun’s energy.

Here’s what you need to do:

1. Disassemble mercury and build a Dyson swarm: a multitude of solar captors around the sun. 
2. Build self-replicating probes
3. Launch the self-replicating probes to every reachable galaxy.

In science fiction, humanity’s expansion into the universe usually starts within our galaxy, the Milky Way. After a new star system is occupied, humanity jumps to the next star, and so on, until we take the whole galaxy. Then, humanity jumps to the nearest galaxy, and the process is repeated.

This is not how we’re going to do it. Our method is much more efficient. We're going to send self-replicating probes to all the reachable galaxies at once. Getting to the furthest galaxies is not more difficult than getting to the nearest ones. It just takes more time. When a probe arrives at its destination galaxy, it will search for a planet to disassemble, build another Dyson swarm, and launch a new wave of probes to reach every star within the galaxy. And then, each probe in that galaxy will restart civilization.

We already hear you protest, though: “this whole thing still seems pretty hard to me,” you say. “Especially the “disassembling mercury” part”. 

But actually, none of these steps are as hard as they first appear. If you analyze closely how they could be implemented you’ll find solutions that are much easier than you’d expect. And that’s exactly what Stuart Armstrong and Anders Sandberg do in their paper “Eternity in six hours: intergalactic spreading of intelligent life and sharpening the Fermi paradox.” This video is based on that paper.

Exploratory engineering and assumptions

What we mean by “easy” here, is that we will require amounts of energy and resources that are small compared to what is at our disposal in the solar system. Also, the technology required is not extremely far beyond our capabilities today, and the time required for the whole feat is insignificant on cosmic scales.

Not every potential future technology will make sense to include in our plan to spread to the stars. We need to choose what technologies to use by reasoning in the style of exploratory engineering: trying to figure out what techniques and designs are physically possible and plausibly achievable by human scientists. The requirement “physically possible'' is much easier to comply with than “achievable by human scientists”, therefore, we introduce two assumptions that serve to separate the plausible from the merely possible:

First: Any process in the natural world can be replicated with human technology. This assumption makes sense in light of the fact that humans have generally been successful at copying or co-opting nature. 

Second: Any task that can be performed can be automated. The rationale for this assumption is that humans have proven to be adept at automating processes, and with advances in AI, we will become even more so. 

Design of the Dyson swarm

Now, we’ve said we are going to launch probes to every reachable galaxy. This means a hundred million to a hundred billion probes. Where do we get the energy to power all these launches? We don’t need to come up with exotic sources of energy we can’t picture yet. We can use the Sun itself! That’s why we are going to build a Dyson swarm.

To be fair, in order to be sure that a Dyson swarm will be sufficient, we need to already have plausible designs for probes and launch systems in mind, but this is a tutorial for pragmatic wannabe grabby civilizations, so we’ll get to that later, when we actually use them.

A Dyson swarm is simply a multitude of solar captors orbiting around the sun. The easiest design is to use lightweight mirrors, beaming the sun’s radiation to focal points where it’s converted into useful work—for example, using heat engines and solar cells.

A Dyson swarm has major advantages compared to a rigid Dyson sphere. A Swarm isn’t subject to internal forces that would make it collapse, and it can be made with simple and conventional materials.

Even a swarm isn’t without potential problems though: the captors have to be coordinated to avoid collisions and occluding each other. But these are not major difficulties. There are already reasonable orbit designs in today’s literature, and the captors will have large amounts of reserves at their disposal to power any minor course correction. The efficiency of the captors will not be an issue either. We will need only a small amount of energy to power our expansion into the universe compared to the energy a Dyson swarm will be able to collect.

The biggest problem to solve is how to get all of the material necessary to build the solar captors. Even assuming the lightest design achievable with today’s materials, that is, lightweight mirrors, you’d need to take apart Mercury to get everything you need for the swarm. And that’s exactly what we’re going to do. 

There are potentially other pathways to get the material, but being able to take apart Mercury is the conservative assumption to make, as weird as it sounds. We are not assuming future super materials that would let us build a swarm with extremely thin and efficient captors, and therefore with way less material.

Mercury looks very convenient to use in comparison to the other planets and the asteroid belt. Its orbit is approximately at the same distance from the Sun as the Swarm’s, and it’s a rocky planet, 70% metallic and 30% silicate. This is material that we can transform into reflective surfaces for the swarm, and use to build heat engines and solar cells. 

The semi-major axis of Mercury's orbit is approximately 60 billion meters long. Therefore, a sphere around the Sun with that radius would have a surface area in the order of 10^22 square meters. The mass of mercury is in the order of 10^23 kilograms. Now let’s assume we’ll use about half of mercury to build the swarm. If we conservatively pretend that the swarm is a solid sphere around the sun, we can take the fraction between half of mercury’s mass and the surface of the sphere we just calculated to get the mass of the sphere per square meter, which is 3.92 kg/m^2. This is plenty! Iron has a density of 7874 kg/m^3, so we can obtain mirrors with a thickness of at least half a millimeter. We can already easily make mirrors this thin, you can order them online if you want. But most probably, we would use a structure with a much thinner film, of the order of 0.001mm, supported by a network of rigid struts.

Disassembling Mercury

Now, let’s disassemble Mercury and build this swarm, shall we? 

We are going to build the Dyson swarm during the process of disassembly. While we get material from the planet, we build more of the swarm, and as we build new captors we get more energy to power more of the planet’s disassembly, and so on. 

Essentially, we need a feedback loop like this:

We mine necessary material, 

We get the material into orbit, 

We make solar collectors out it, 

We get the energy from the collectors, 

And we use that energy to mine more material, and so the cycle repeats.

Sandberg and Armstrong assume a seed of 1 km^2 of solar panels constructed on Mercury to start the feedback loop. After the seed, the loop can begin with mining the initial material.

At each cycle we have more energy at our disposal to power more mining, and the process can easily speed up exponentially. 

In fact, the feasibility of Mercury's disassembly hinges on if we get an exponential feedback loop or not. If we can’t complete the loop, or if it’s not at least near exponential, then we’re out of luck. The process would grind to a halt or take too long to complete in any reasonable amount of time. If we want the energy at our disposal to increase exponentially, the number of captors must increase by a fixed percentage at each cycle. That means that the energy required to mine materials, get them into orbit, and make captors, must remain nearly constant or decrease at each cycle. But this is not a big concern. Mining material and making solar collectors shouldn't consume more energy as the disassembly progresses. On the contrary, towards the end of the disassembly, less energy will be required to get material into orbit, as Mercury’s gravity will be much easier to overcome. A potential problem could be cooling Mercury’s core, but this is a fixed cost, and Mercury’s heat might be harvested to get more energy.

And now, maybe you’re thinking: “Wait, even if we can get an exponential feedback loop in theory, how on Earth are we going to get the workers to do all this?” And that’s where our assumption that “any task that can be performed, can be automated” comes in. With automation, the sheer scale of projects is simply not a problem. New machines and factories can be built essentially without human intervention. Time, material, and energy become the only things we need. Encouragingly, NASA had a design for a self-replicating lunar factory in 1980. And surely, in the future we will be able to do much better than NASA in the eighties!

Sandberg and Armstrong make a few additional assumptions to precisely estimate how long it’ll take to complete the Dyson swarm. 

They assume: 

• Solar captors with an efficiency of ⅓.
• Only 1/10 of the energy will be used to propel material into space. The rest will be used for mining, reprocessing material, or simply lost.
• It takes five years to process the material into solar captors and place them into the correct orbit. 
• Only half of Mercury’s material will be used to construct the captors. 

Under these assumptions, the power available will increase exponentially every 5 year cycle. Mercury will be disassembled in 31 years, with most of the mass harvested in the last four years. 

But as long as the exponential feedback loop is possible, the details aren’t that important, and we will complete the disassembly within a few cycles and a short amount of time. 

And even if an exponential feedback loop turns out not to be possible, it doesn’t necessarily mean we can’t build the Dyson swarm. This is just one way to attack the problem, which relies on plausible future technology constrained by conservative assumptions. For example, if we're able to produce super materials, taking apart a large asteroid might be sufficient.

Design of the probes

Now that we've built the Dyson swarm, we have the energy to launch countless self-replicating probes into the universe. 

Our probes should be capable of safely landing on other planets or asteroids, use the resources there to make copies of themselves, build other dyson swarms, launch another wave of probes, and ultimately start civilization on other star systems.

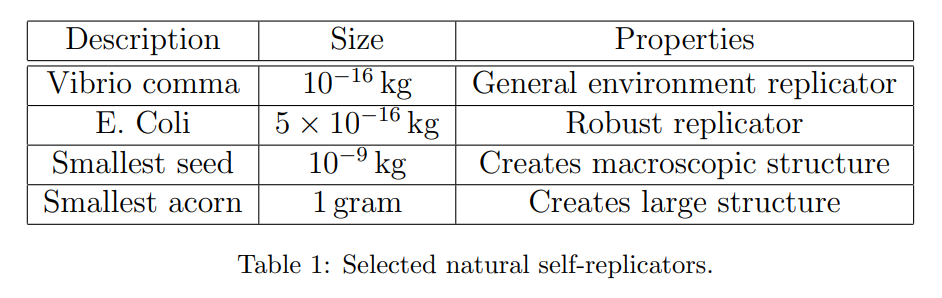
By guessing that building self-replicating probes will be possible with future technology, we are essentially making use of the assumption “Anything possible in the natural world can also be done under human control”. Every living thing is capable of replicating. Here’s a table of some of the smallest replicators in nature. The smallest seeds on Earth weigh a millionth of a gram, and the smallest acorn weighs 1 gram. Think about it: an acorn is a solar-powered factory for the production of more acorns that generates large structures in the process: namely, oak trees.
 

When thinking about the size of our probes, we need to make a distinction between the self-copying piece of the system, and the whole object that gets launched, which may include fuel, rockets for deceleration, and other equipment. 

A reasonable upper limit for the size of the replicators is 500 tons. This is the size of the replicator in NASA’s self-replicating lunar factory design, which made very conservative assumptions. 

As a lower limit we can use a design of molecular assembler by Robert Freitas and Ralph Merkle, from their landmark book “Kinematic Self-Replicating Machines”, a comprehensive review of self-replicating designs up until 2004. The mass of this replicator would be in the order of 10^-18kg. For reference, this is about thirty thousand times smaller than a red blood cell.

The data storage on the probe would probably be of insignificant mass. An extremely compact design would be diamond constructed with carbon 12 and carbon 13. The two isotopes would encode the bits 0 and 1. A memory like this would have a capacity of six billion terabytes per gram. Or we could use a data storage mechanism with the same compactness as DNA, in the order of a hundred million terabytes per gram. As a comparison, the total amount of data in the human world in 2020 could be stored in about 500 grams of DNA-level storage.

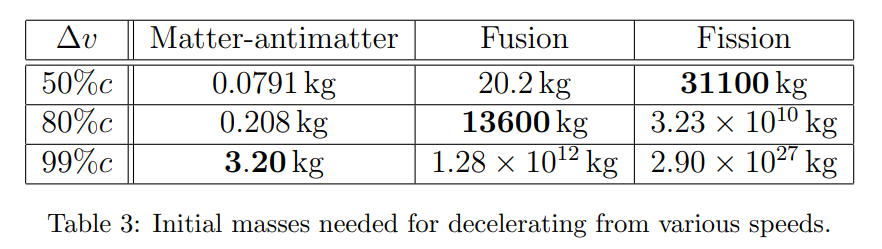
Apart from the replicator, the probe needs fuel to decelerate when approaching its destination. Sandberg and Armstrong hypothesize three possible types of fuel to power the deceleration. In order of increasing speculativeness and efficiency, they are: nuclear fission, nuclear fusion, and matter-antimatter annihilation. As you can see in this table, they calculated the mass of fuel needed given different deceleration amounts and type of fuel. In the table, the replicator is assumed to weigh 30 grams. You can take the “delta v” column as also indicating “starting velocities” if the probe then decelerates to zero. The values in bold are the kilograms of fuel needed given the most reasonable combinations of starting velocities and type of fuel available.

This table doesn’t take into account many things that could aid deceleration though:

For example, the trajectory of the probe might be designed to use gravitational assists to slow down. Or magnetic sails could be used to create drag against the local magnetic field in the destination galaxy. Moreover, the expansion of the universe means that some amount of deceleration will come for free, and probes launched to distant galaxies would arrive with little velocity. In that case, we would need fuel only for maneuvering at the end. There are many other speculative options to help decelerating, such as the Bussard ramjet, which uses enormous magnetic fields to collect hydrogen atoms from the interstellar medium and compress them to achieve nuclear fusion.

Another potential design choice for the probes is to equip them with shields. Intergalactic space is not empty. The probes might encounter dust, and at relativistic speeds, collisions can easily destroy our probes. Another solution is simply to launch redundant probes to compensate for the fact that some might be destroyed. Sandberg and Armstrong estimate that, for speeds of 50% to 80% the speed of light, launching two probes per galaxy is enough to expect that at least one will arrive. If the probes travel at 99% of the speed of light, then we’d need to launch 40 probes to each galaxy. 

The launch phase

Alright, now let’s say we’ve chosen a viable design for the probes. Their construction has taken little material compared to the Dyson swarm. The final combined mass of all of the probes, redundancy included, is in the order 10^11 to 10^12 kilograms. This is about the mass of a mountain. The Dyson swarm is operational, and provides us with all the energy we need. It is time to launch the probes.  

We will not use rockets, but a fixed launch system. Rockets would be needlessly difficult and inefficient to use for achieving acceleration to relativistic speeds. They need to carry fuel, which would in turn need to be accelerated, and the fuel needed increases exponentially with the change of speed we want to achieve. Fixed launch systems sidestep this, and are often reusable. For example we could use coilguns. Essentially, long barrels around which coils are arranged and switched on and off with precise timings, causing the probe in the barrel to accelerate due to the magnetic forces generated by the coils. With coilguns, we would shoot our probes into space. In combination, or by themselves, we can also use solar sails accelerated by lasers or particle beams.

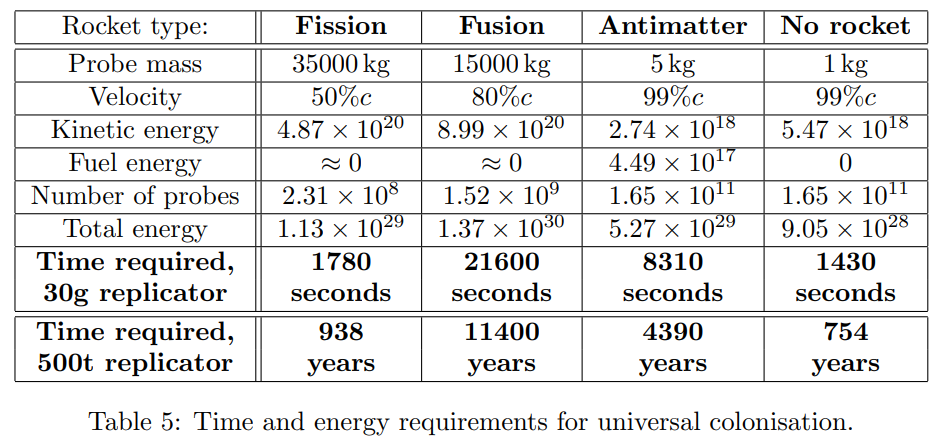
Now, look at this table: for each type of probe and for each type of replicator, you can find in bold the time required to power the launch if the energy of the Dyson swarm were entirely devoted to the task. In the case of the 30g replicator, the numbers are insignificant on a human scale. 6 hours of the sun’s energy is the maximum we would need. Instead, if the replicator is the 500 tons version, we would need hundreds of years of the Sun’s energy. But this also looks very feasible if you consider that humanity might survive millions of years, and over time might divert some energy from the dyson swarm to power launches, and not necessarily launch all the probes at once. 
 

After the universe, the galaxy

Now, picture a future President of the Solar System proclaiming: “everyone turn off their virtual reality sets for six hours, we’re taking over the universe!”

The probes are launched to every reachable galaxy and the travel begins. 

Once this first wave is enroute we can launch a new wave of probes within the milky way at lower speeds. So we’d start expanding into our own galaxy only after having started expanding into the wider universe! 

Meanwhile, the probes we’ve launched to other galaxies will progressively continue to start new civilizations for the following 10 billion years, and after that, our expansion will be complete. Ten billion years may sound like a lot, but the universe will last for trillions of years. Future humanity will have plenty of time to enjoy even the most distant galaxies.

Armstrong and Sandberg calculated that at speeds between 50% and 99% of the speed of light, the probes will reach 116 million to 4 billion galaxies. The higher the speed, the more galaxies the probes can reach, because the universe is expanding at an accelerating pace, and as time passes an increasingly large number of galaxies becomes forever out of reach if we can’t find a way to sidestep the speed of light limit. 

Final considerations

And now that every step is complete, you know how to take over the universe. You don’t need to do everything exactly in this way, though. This paper proposed many possible designs and methods at each step, but there are certainly many more ways to go. Moreover, Armstrong and Sandberg used conservative assumptions; the real designs will probably be better. The point of the paper was to illustrate that the feat is in principle possible with cosmically insignificant amounts of energy and time.

One additional point motivating the paper is that since spreading through the universe doesn’t require a lot of resources, that means that the Fermi paradox is a lot sharper than we imagined. There are millions of galaxies that could have potentially reached us by now. And yet, we don't see any alien colonization projects in our local neighborhood. This could simply mean that there is pretty much no one else out there, or another answer could be the one given in the grabby aliens videos. If we could have seen aliens they would be here now instead of us.

If there are indeed aliens out there, that means our time to begin expanding into the universe is even more limited than we previously thought. Not only is the universe expanding at an accelerating rate, making more and more galaxies forever out of reach, but aliens might also be out there grabbing galaxies instead of us! 

So, what are we waiting for? Let’s go and do it ourselves! Let's take over the universe!

Sources and more readings

Eternity in six hours: intergalactic spreading of intelligent life and sharpening the Fermi paradox, by Anders Sandberg and Stuart Armstrong:
http://www.fhi.ox.ac.uk/wp-content/uploads/intergalactic-spreading.pdf

NASA's self-replicating lunar factory design:

- https://space.nss.org/wp-content/uploads/1982-Self-Replicating-Lunar-Factory.pdf

- http://www.rfreitas.com/Astro/GrowingLunarFactory1981.htm

Kinematic self-replicating machines, by Freitas and Merkle: https://www.amazon.com/Kinematic-Self-Replicating-Machines-Robert-Freitas/dp/1570596905

The quote at 15:11 is almost an actual quote from the paper!