Dialogue
[Warning: the following dialogue contains an incidental spoiler for "Music in Human Evolution" by Kevin Simler. That post is short, good, and worth reading without spoilers, and this post will still be here if you come back later. It's also possible to get the point of this post by skipping the dialogue and reading the other sections.]
Pretty often, talking to someone who's arriving to the existential risk / AGI risk / longtermism cluster, I'll have a conversation like the following.
Tsvi: "So, what's been catching your eye about this stuff?"
Arrival: "I think I want to work on machine learning, and see if I can contribute to alignment that way."
T: "What's something that got your interest in ML?"
A: "It seems like people think that deep learning might be on the final ramp up to AGI, so I should probably know how that stuff works, and I think I have a good chance of learning ML at least well enough to maybe contribute to a research project."
T: "That makes sense. I guess I'm fairly skeptical of AGI coming very soon, compared to people around here, or at least I'm skeptical that most people have good reasons for believing that. Also I think it's pretty valuable to not cut yourself off from thinking about the whole alignment problem, whether or not you expect to work on an already-existing project. But what you're saying makes sense too. I'm curious though if there's something you were thinking about recently that just strikes you as fun, or like it's in the back of your mind a bit, even if you're not trying to think about it for some purpose."
A: "Hm... Oh, I saw this video of an octopus doing a really weird swirly thing. Here, let me pull it up on my phone."
T: "Weird! Maybe it's cleaning itself, like a cat licking its fur? But it doesn't look like it's actually contacting itself that much."
A: "I thought it might be a signaling display, like a mating dance, or for scaring off predators by looking like a big coordinated army. Like how humans might have scared off predators and scavenging competitors in the ancestral environment by singing and dancing in unison."
T: "A plausible hypothesis. Though it wouldn't be getting the benefit of being big, like a spread out group of humans."
A: "Yeah. Anyway yeah I'm really into animal behavior. Haven't been thinking about that stuff recently though because I've been trying to start learning ML."
T: "Ah, hm, uh... I'm probably maybe imagining things, but something about that is a bit worrying to me. It could make sense, consequentialist backchaining can be good, and diving in deep can be good, and while a lot of that research doesn't seem to me like a very hopeworthy approach, some well-informed people do. And I'm not saying not to do that stuff. But there's something that worries me about having your little curiosities squashed by the backchained goals. Like, I think there's something really good about just doing what's actually interesting to you, and I think it would be bad if you were to avoid putting a lot of energy into stuff that's caught your attention in a deep way, because that would tend to sacrifice a lot of important stuff that happens when you're exploring something out of a natural urge to investigate."
A: "That took a bit of a turn. I'm not sure I know what you mean. You're saying I should just follow my passion, and not try to work towards some specific goal?"
T: "No, that's not it. More like, when I see someone coming to this social cluster concerned with existential risk and so on, I worry that they're going to get their mind eaten. Or, I worry that they'll think they're being told to throw their mind away. I'm trying to say, don't throw your mind away."
A: "I... don't think I'm being told to throw my mind away?"
T: "Ok. The thing I'm saying might not apply much to you, I don't know. But there's a pattern that seems common to me around here, where people understandably feel a lot of urgency about the thing where the world might be destroyed, or at least they feel the urgency radiating off of everyone else around them, or at least, it seems as though everyone thinks that everyone ought to feel urgency. Then they sort of transmute that urgency, or the sense that they ought to be taking urgent action, into learning math or computer science urgently or urgently getting up to speed by reading a lot of blog posts about AI alignment. It's not a mistake to put a ton of effort into stuff like that, but doing that stuff out of urgency rather than out of interest tends to cause people to blot out other processes in themselves. Have you seen Logan's post on EA burnout?"
A: "Yeah, I read that one."
T: "Another piece of the picture is that there's an activity of a growing mind that I'm calling "following your interest" or "fun" or "play", or maybe I should say "thinking hard" or "serious play", and that activity is another thing that can get thrown under the bus. That activity is especially prone to be thrown under the bus, and it's especially bad to throw that activity under the bus. The activity of thinking hard as a result of play is especially prone to be thrown under the bus because it's a highly convergent subgoal, and so, like in Logan's post, it's one of those True Values that gets replaced by a Should Value. The activity of being drawn into playful thinking that becomes thinking hard is especially bad to throw under the bus because it's a central way that a mind grows. So if you're not giving yourself the space to sometimes be drawn into playful thinking, then you're missing out on deepening your understanding of stuff that you could have been playfully thinking hard with, and also you're letting that muscle atrophy."
A: "Let me see if I've got what you're saying. There's two kinds of thinking, the True thinking and the Should thinking. And the Should thinking is worse than the True thinking, but people do the Should thinking?"
T: "Er, something like that... except that the phrase "Should thinking" is ambiguous here, and that's important. There's fake Should thinking, or let me say "Urgent fake thinking", which isn't really thinking, in that it doesn't take in and integrate much information, or notice contradictions, or deduce consequences of beliefs, or search for hypotheses and concepts, or make falsifiable predictions, or distill ideas. For example, rehearsing arguments that you read in a blog post, in response to rehearsed questions, usually isn't thinking, it's usually fake thinking."
A: "Got it, got it."
T: "Then there's Urgent real thinking, which is actually thinking, and has the structure: there's this way I want the world to go; how can I make the world go that way? Both backward chaining and forward chaining would be Urgent real thinking. It would also be Urgent real thinking to ask: What sort of scientific understanding would I have to have, in order to satisfy this subgoal of making the world go the way I want it to? And then doing that science. All of that activity has the structure of: I see how thinking about this stuff should help with getting the world to go a certain way. On the other hand, there's Playful thinking. Playful thinking doesn't have to have a justification like that; it's coming from a different source. So Urgent thinking has a tendency to be fake thinking, and even Urgent real thinking has a tendency to squash Playful thinking, and that these two things are connected."
A: "Sorry, what do you even mean by Playful thinking?"
T: "Yeah, sorry, I should have been more clear. It's sort of subtle, or even sacred if you'll permit me to use that word, so it's hard to just define or, like, comprehensively describe. I know it as a phenomenon, something I encounter, without knowing what it really is and how it works and stuff. Anyway, it's something like: the thoughts that are led to exuberantly play themselves out in the natural course of their own time. This isn't supposed to be something alien and complicated, this is supposed to be a description of something that you're already intimately familiar with, even made out of, and that you definitely did when you were a kid. It's probably whatever was happening with you that led you to make hypotheses about what that octopus was doing."
A: "Could you give an example of Playful thinking?"
T: "Gah, I really need to write this up as a blog post. Giving an example that I'm not really into at the moment seems kind of bad. But ok, so, [[goes on a rambling five-minute monologue that starts bored and boring, until visibly excited about some random thing like the origin of writing or the implausibility of animals with toxic flesh evolving or emergent modularity enabled by gene regulatory networks or the revision theory of truth or something; see the appendix for examples]]"
A: "Ok I think I have some idea of what you're talking about. But it sure sounds like what you're recommending is just inefficient? It seems like there's a bunch of smart people who have thought about alignment a lot more than I have, and they've said that there's all this stuff like linear algebra and probability theory that's useful for alignment, so it seems reasonable to learn that stuff. And I can learn it faster if I focus on it, instead of getting distracted, right? I think if I followed your advice I'd just goof off a lot."
T: "I'm definitely not saying not to dive in deep, go fast, et cetera. I'm saying to not not also do non-Urgent thinking. Like, if you find yourself noodling or doodling, don't stop yourself due to the overwhelming urgency of reading the next page of the textbook. Even assuming that you're just trying to learn some list of material as fast as possible, playful thinking is still needed. There's a thing I like to do, where I'll stare at a mathematical object, and keep staring until it sort of reaches "semantic satiation", and I can see it in a more naive way. And then I can tweak it, or look at it upside down, or combine it with something else, or ask why it has to be this way or that way rather than some other way. And this feels like playing, but I think it gives me the ideas more thoroughly, and then they're more useful to me in other contexts. So even from a backchaining point of view it ends up getting you something that a more functional goal, like "can I do the exercises in the textbook", doesn't always get you."
A: "I'm a little confused. Before I thought you were saying that people should let themselves get nerdsniped more, instead of only thinking about stuff that's planning ahead to what they want to work on. Now it sounds like you're saying there's some other way to do math that's more useful for alignment work?"
T: "Those two recommendations are connected. Both of those recommendations are consequences of the following proposition: your mind knows a lot about what's worth thinking about that "you" don't know, in some sense. And you can't just get that stuff by asking your mind to tell you that stuff; you have to let your mind do its thing sometimes, without requiring a legible justification. The name "nerdsniping" doesn't seem quite right, though. "Nerdsniping" is where someone else crafts a puzzle that catches your attention. That can be fun and good, but to my taste, it tends to have a flavor of being a bit too cute or clever. I want to point instead at something that involves eternity and elegance. Things that have an eternity to them--e.g. Euclidean space, the invention of words, embryogenesis--are more likely to draw your mind along into thinking, and they do that without being clever or polished, because the natural world is just like that. Elegance has something to do with eternity, like how the architecture of a church evokes something that normal buildings don't, or how a clear mathematical definition doesn't have superfluous complications. Elegance is something that your mind instinctively tries to find or create."
A: "Would elegance really help with learning things faster? It seems like, yeah, I could spend a long time getting a really good understanding of one thing, and that would have some benefits, like I could apply it faster. But it seems more important to get a pretty good understanding of a lot of things, so I can start combining ideas and understanding where the alignment field is currently at and thinking about how I can contribute."
T: "An analogy here is that covering a lot of ground too quickly is like programming a project just using the built-ins you already know, using repetitive that hacks aren't easy to understand or modify later and that have interfaces enmeshed with other functions. You can go fast in the short term, but in the longer term, you're going to come back and have a hard time understanding why the code is the way it is, and you'll probably have to do a bunch of work refactoring things to separate concerns so that you can understand the code well enough to modify it efficiently. Playing with ideas is like learning the built-ins that are appropriate to the task at hand, and factoring your code so pieces are reusable, and taking the time to reduce terms that do stuff like have intermediate variable assignments that can be eliminated with no detriment, and factoring out repetitive pieces of code into a single generalized function."
A: "Would people around here really disagree with that? I still don't feel like I'm being told to throw my mind away."
T: "I don't know. Maybe most people would agree with what I'm saying, at least verbally, and even consider it obvious. But also empirically people tend to get the message that they should orient with some kind of urgency and all-consuming attention around existential risk. This could be mediated implicitly, through patterns of attention. Like, someone tells you "Give yourself plenty of time for other pursuits, and make sure to leave a line of retreat from this existential risk stuff.", which is good advice, and then also only get excited talking to you if you're describing your plan for how to prevent the world from being destroyed by AGI. Also, people arriving here with an attitude of deference, e.g. studying textbooks that other people told you to study, are prone to be very attuned to that sort of message. Even if no one were sending those messages, some people would impute those messages to their social context. A pattern I have noticed in myself, for example, is: "Oh, I'm feeling energetic at the moment, so now is a good time to sit down and actually think hard about alignment.", instead of seeing what I actually feel like doing given permission to decide to do something for the fun of it, and this behavior pattern seems like a recipe for getting into an unhelpful rut."
A: "Ok, I think I'm getting the picture. I'll make an effort to have more fun with math, and hopefully I'll learn it more deeply. That seems useful."
T: "Ack."
A: "Oh no. What did I do? :)"
T: "It's just that there's a danger in having fun with math because it helps you learn it more deeply, rather than because it's fun. Talking about how it helps you learn it more deeply is supposed to be a signpost, not always the main active justification. A signpost is a signal that speaks to you when you're in a certain mood, and tells you how and why to let yourself move into other moods. A signpost is tailored to the mood it's speaking to, so it speaks in the language of the mood that it's pointing away from, not in the language of the mood it's pointing the way towards. If you're in the mood of justifying everything in terms of how it helps decrease existential risk, then the justification "having fun with math helps you learn it better" might be compelling. But the result isn't supposed to be "try really hard to do what someone having fun would do" or "try really hard to satisfy the requirement of having fun, in order to decrease X-risk", it's supposed to be actually having fun. Actually having fun is a different mood from justifying everything in terms of X-risk. Imagine a six-year-old having fun; it's not because of X-risk."
A: "How am I supposed to try to have fun, without trying to have fun?"
T: "Come home to the unique flavor of shattering the grand illusion. Come home to Simple Rick's."
A: "That was a terrible Southern accent."
T: "Fair enough. Anyway, you might have been trained in school to falsify your preferences by pretending to have fun doing stupid activities. So you could try to do the opposite of everything you'd do in school. You could also try a "Do Nothing" meditation and see what happens. It might also help to think of having fun sort of like walking: you know how in some sense, and you even have an instinct for it; having fun, if you've forgotten, is more a question of letting those circuits--which don't require justification and just do what they do because that's what they do--letting those circuits do what they do, and enjoying that those circuits do what they do. Basically the main thing here is just: there's a thing called your mind, your mind likes to play seriously, and consider not preventing your mind from playing seriously."
A: "Got it."
T: "The end."
Synopsis
- Your mind wants to play. Stopping your mind from playing is throwing your mind away.
- Please do not throw your mind away.
- Please do not tell other people to throw their mind away.
- Please do not subtly hint with oblique comments and body-language that people shouldn't have poured energy into things that you don't see the benefit of. This is in conflict with coordinating around reducing existential risk. How to deal with this conflict?
- If you don't know how to let your mind play, try going for a long walk. Don't look at electronics. Don't have managerial duties. Stare at objects without any particular goal. It may or may not happen that some thing jumps out as anomalous (not the same as other things), unexpected, interesting, beautiful, relatable. If so, keep staring, as long as you like. If you found yourself staring for a while, you may have felt a shift. For example, I sometimes notice a shift from a background that was relatively hazy/deadened/dull, to a sense that my surroundings are sharp/fertile/curious. If you felt some shift, you could later compare how you engage with more serious things, to notice when and whether your engagement takes on a similar quality.
Highly theoretical justifications for having fun
Throwing your mind away makes life worse for you, and you should be wary of doing things that make life worse for you. This is the blatantly obvious central thing here.
Interrupting playful thinking causes learned helplessness about playful thinking. (Imagine knocking over a toddler's blocks whenever they are stacked three-high or more.) On the other hand, giving yourself to playful thinking makes it so that playful thinking expects to be given you, so playful thinking disposes itself to play.
Playful thinking puts ideas into a form where they're more ready to combine deeply with other ideas.
Playful thinking indexes ideas more thoroughly, so that they come up when helpful and in helpful ways.
Your senses of taste, interest, fun, and elegance know [stuff about what's worth thinking about] that isn't known by you or by those whose advice you take. Analogously, your sense of beautiful code knows stuff about good programming that you don't know.
Play is non-specific practice. It accesses canonical and practiceworthy structure.
Playful thinking sets up questions in your brain that you wouldn't have known how to set up just by explicitly trying to set up questions. A question is a record of a struggle to deal with some context. These questions, like the dozen problems Feynman carries around with him, set you up to connect with new ideas more thoroughly.
Play exercises the ability of setting up problem contexts and discerning interesting problem contexts. This ability is extremely under-exercised by more deferential ways of learning, and is especially needed in pre-paradigm fields.
Play is a long-term investment in deep understanding.
Many people are far from maximally exerting themselves. Someone who is far from maximally exerting themselves can't have very large and fundamental tradeoffs between exerting themselves towards one or another purpose, such as having fun vs. doing alignment research. Instead of trading off between two activities, they could exert themselves more if they had more exertion-worthy activities available. Playfully thinking hard is a suprisingly exertion-worthy activity.
Being initially drawn into playful thinking correlates with and grows into being drawn further into more elaborated playful thinking, which is continuous with any real thinking. Your thoughts about strategy, the alignment problem, or whatever important thing, can inform and be informed by your taste in what to playfully think about, without having to be the justification for your playful thinking.
Many ideas are provisional: they have yet to be fully grasped, made explicit, connected to what they should be connected to, had all their components implemented, carved at the joints, made available for use, indexed. Many important ideas are provisional. Playing with provisional ideas helps nurture them.
Your sense of fun usefully decorrelates you from others, leading you to do computations that others aren't doing, which greatly improves humanity's portfolio of computations.
You're more exercising ἀρετή ("excellence", cognate to "rational") when doing things that your mind is drawn to do by its own internal criteria.
Your sense of fun decorrelates you from brain worms / egregores / systems of deference, avoiding the dangers of those.
Brain worms / egregores / systems of deference that would punish you for devoting energy to playful thinking, are likely to be ineffective at achieving worthwhile goals, among other things because they cut off the natural influx of creativity that solves novel problems. A social coordination point can appear powerful just by being predominant, and therefore appears desirable to join, without actually being worthwhile to join.
Requiring that things be explicitly justified in terms of consequences forces a dichotomy: if you want to do something for reasons other than explicit justifications in terms of consequences, then you either have to lie about its explicit consequences, or you have to not do the thing. Both options are bad.
Intensity in the face of existential risk is appropriate. To enable intensity in the face of existential risk, don't require yourself to throw your mind away in order to be intense.
Appendix: What is this "fun" you speak of?
What's a circle?
Take a smooth closed curve C in the plane. These conditions are equivalent:
- There is a point p such that all points on C are equidistant from p.
- C has constant curvature.
- (If C bounds a disc) C bounds the maximum area that's possible to bound with a curve of the same length as C.
- The group of isometries of the plane that maps C to itself is a nontrivial connected compact topological group.
These conditions all define a circle in the plane. But what happens if instead of a plane, we look at some other manifold? See here for some disussion.
Hookwave
It's 0400 and it's raining heavily. Tributaries swell along curbs, then clatter down drains to join the subterranean sewerriver. In the middle of one street, the downward slope perpendicularly away from the curb exceeds the slope along the curb, sending the curb's tributary across to the other side of the streed. Hundreds of criss-crossing lines checker the flowing sheet of water that is spread out over the concrete. How does that make sense? It looks as though water is flowing in two skewed directions, one sheet flowing over or through the other sheet. Are these just wakes from the bumps in the asphalt? But it really looks like the water is flowing in both skew directions. Maybe all the little wakes are making ripples, so there are waves traveling in both directions?
In another curb's rivulet, there's an oddly-shaped wave. Most curb rivulets have lots of little wakes in them from bumps in the asphalt or from influxes reflecting off the curb. These little wakes usually curve so they join with the flow: they start off at some angle away from the boundary of the rivulet towards the center of the rivulet, and then curve to be more parallel with the direction of flow. But not this hookwave:

It's curving off flowward and to the right, so that its angle with the direction of flow increases flowward:

Why is it like that? Why is this wake different from all other wakes? This one and a few other hookwaves always come right after a divot in the concrete against the curb. If a foot (waterproofed, dry-socked) is placed just upstream of the divot, blocking the half of the rivulet that's further from the curb, then the hookwave straightens out a bit, like a more usual wake, contra the intuition that the flowing water should be "sweeping back" the hookwave. Does the flowing water instead "pile up" to form the hook?
Random smooth paths
This cemetary is large and round, so it has a network of internal paths. At each intersection there are 2 or 3, or occasionally 4 or 5 directions to continue in, "somewhat forwardly", without doubling straight back. Choosing randomly would follow a sort of constrained random walk: there's a kind of inertial or smoothness condition, where random turns are allowed but doubling back is disallowed. What sort of random walk is that? Staying on the paths and keeping off the grass reduces the random walk to a random (asymmetric) walk on a(nother) graph.
What if the grass isn't off limits, and there are choices at every moment which way to turn, rather than just at intersections? The Wiener process (which describes Brownian motion) could describe this kind of walk. But a Wiener process is infinitely jagged; the wheel gets turned arbitrarily sharply, arbitrarily densely in time. It's very far from smooth.
What if the path has to be an analytic function (comes from a Taylor series)? Then it's smooth, but it's also determined everywhere if it's determined on a small patch. So it's not intuitively random. A random path should have some independence between changes that happen at different points.
What about smooth paths? Smooth paths are nice, in that they at least have all derivatives at all points, and aren't determined by local patches, and can be stitched together (if given a bit of breathing room). Is there a nice notion of a smooth random walk? More detail here.
Mandala
Lying on the grass between the sidewalk and an Oakland street:

What sort of symmetry does this mandala have? The purple petals around the outer rim have sixteenfold rotational symmetry (and we could allow reflections, giving ). The purple petals near the center have eightfold rotational symmetry. Centerward of the innermore purple petals, we have 28-fold, 24-fold, and 32-fold symmetry, and then the red band has a full circle's symmetry. The innermost ring has 12-fold symmetry. So as a whole the mandala has 4-fold symmetry.
Abstractly, there's an embedding of into each of , , , , and , and is the biggest group that embeds into all those groups. That's just a fancy way of saying that four is the greatest common divisor of all those numbers. We could also say that there's an embedding of into each of , , , , and .
Given some set of groups, is there always a unique greatest common subgroup? What are greatest common subgroups for some pairs of finite groups? Given some groups and a greatest common subgroup , is there always a corresponding "mandala"--a geometric figure that's a union of figures such that the symmetry group of each is exactly and the symmetry group of is exactly ?
Water flowing uphill
The slope of this segment of the street is by all passerby accounts, eh, hard to tell but a bit uphill, coming from this direction. It has rained an hour ago. In the narrow channel between the curb and the retaining wall, there's water flowing. Which direction is it flowing? The water is flowing uphill. What.
Guitar chamber
The hollow chamber of an acoustic guitar makes the sound of a plucked string fuller. And louder? Does it? It's something about "resonance" and "interference". But how could the chamber make the sound louder? Isn't all the energy that's bleeding off from the vibrating string already being emitted as sound waves?
Maybe it's that the sound waves at the wavelengths that fit in the chamber don't interfere with themselves. But how would that make them louder? Do they "build up" over a few milliseconds? But that doesn't make them louder, the sound waves are still leaving the guitar pretty much the whole time while the string is picked, they're not built up and then released in a loud burst.
Maybe the chamber just redirects the sound forward, so it's all going in one direction, and it's louder in that direction but quieter behind the guitar?
Maybe the chamber isn't making the sound louder by adding energy, but just putting the soundwaves at different frequencies all into one frequency. That could make it sound louder, maybe? Why exactly would that sound louder? How does it put the energy from one frequency into another frequency? And also, how does whistling work? Or speaking, or howling wind?
Groups, but without closure
A group is a set of transformations that has an identity transformation that doesn't do anything, inverse transformations that undo transformations, and composite transformations that are the result of doing one transformation followed by doing another transformation.
What happens if we tweak this concept to see how it works? What if there isn't an identity transformation? Why, that's just an inverse semigroup, of course. Mathematicians have got names for all those sorts of things:
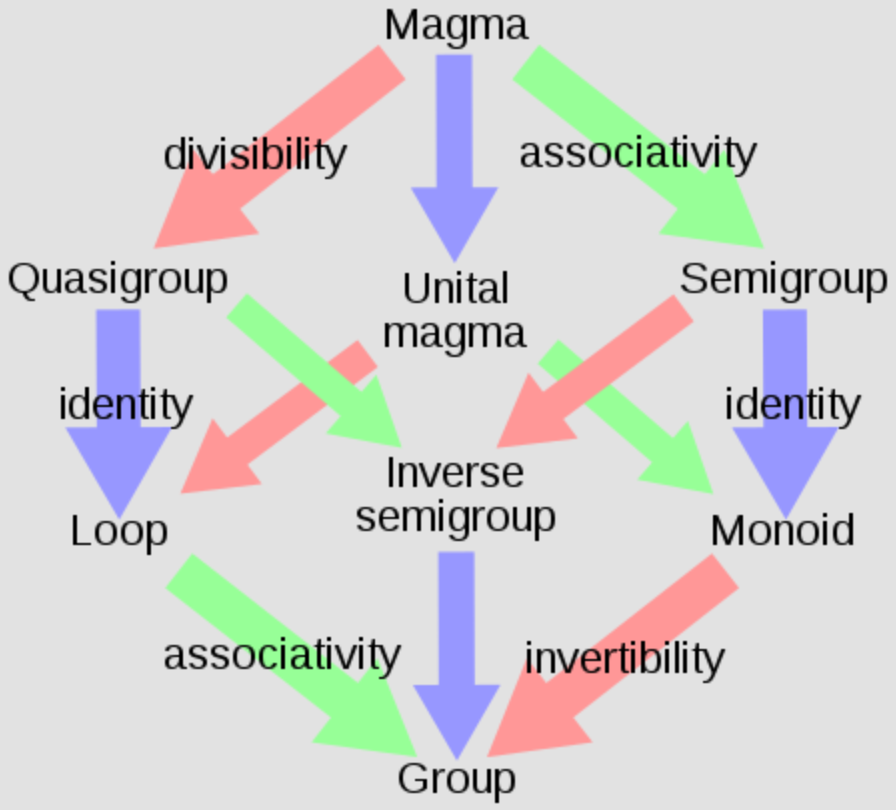
(From Wikipedia)
But what about closure under composition? It makes sense that transformations are closed under composition: if you do one transformation and then do another, you've done some kind of transformation. So whatever you've done, that's the transformation that's the composition of the two component transformations.
But what if there were two transformations that you could do individually, but that you couldn't do one after the other? For example, look at the set of transformations of the form: I pick up this heavy box and move it to another spot on the ground. There's an identity transformation (do nothing), and there's usually an inverse transformation (if I moved the box 10 feet northwest, now I move it 10 feet southeast, and now it's as if I've done nothing). But what if I get too tired of moving the box after moving it a mile? Then I can move the box 1 mile northwest, but I can't do that transformation twice.
So what we have is some kind of "almost a group". What do these things look like? What are some interesting things that can happen with "almost a group"s that can't happen with groups? Is there a nice classification of them? (Compare approximate groups.)
Wet wall
Sometimes walls are wet.




Sometimes they're wet shaped like a V, and sometimes like an A. Why, exactly?
Thanks to Justis Mills for feedback on this post.

This is a great post and I really agree. I'm becoming more suspicious lately of my former beliefs (aliefs?) of 'if you're not feeling emotional urgent about x cause or y activity, it's because your emotions are wrong'. Now, I see my felt senses of eagerness or interest or motivation as containing more information, even if they tell me to work on or care about things that EAs don't usually work on or care about.
People who like Logan's post on EA burnout will love Tyler Alterman's post on Effective altruism in the garden of ends. Both are close to my own experience.