BLUF: 3 000 and $3\cdot {10}^3$ are equivalent; so too a probability of 10% and 9-to-1 odds; and so too 0.002 and 1/500. Despite their objective equivalence, they can look very different to our mind’s eye. Different notation implies particular scales or distributions are canonical, and so can frame our sense of uncertainty about them. As the wrong notation is can bewitch us, it should be chosen with care.

Introduction

I presume it is common knowledge that our minds are woeful with numbers in general and any particular use of them in particular. 

I highlight one example of clinical risk communication, where I was drilled in medical school to present risks in terms of absolute risks or numbers needed to treat (see). Communication of relative risks was strongly discouraged, as:

Risk factor X increases your risk of condition Y by 50%

Can be misinterpreted as:

With risk factor X, your risk of condition Y is 50% (+ my baseline risk)

This is mostly base-rate neglect: if my baseline risk was 1 in a million, increasing this to 1.5 in a million (i.e. an absolute risk increase of 1 in 2 million, and a number needed to treat of 2 million) probably should not worry me.

But it is also partly an issue of notation: if risk factor X increased my risk of Y by 100% or more, people would be less likely to make the mistake above. Likewise if one uses different phrases than ‘increases risk by Z%’ (e.g. “multiples your risk by 1.5”). 

I think this general issue applies elsewhere

Implicit scaling and innocent overconfidence

A common exercise to demonstrate overconfidence is to ask participants to write down 90% credible intervals for a number of ‘fermi-style’ estimation questions (e.g. “What is the area of the Atlantic Ocean?”, “How many books are owned by the British Library?”). Almost everyone finds the true value lies outside their 90% interval much more often than 10% of the time.

I do not think poor calibration here is solely attributable to colloquial-sense overconfidence (i.e. an epistemic vice of being more sure of yourself than you should be). I think a lot it is a more innocent ineptitude at articulating their uncertainty numerically.

I think most people will think about an absolute value for (e.g.) how many books the British Library owns (“A million?”). Although they recognise they have basically no idea, life in general has taught them variance (subjective or objective) around absolute values will be roughly symmetrical, and not larger than the value itself (“they can’t have negative books, and if I think I could be overestimating by 500k, I should think I could be underestimating by about the same”). So they fail to translate (~appropriate) subjective uncertainty into corresponding bounds: 1 000 000 $\pm$ (some number less than 1 million)

I think they would fare better if they put their initial guess in scientific notation: $1\cdot {10}^6$. This emphasises the leading digit and exponent, and naturally prompts one to think in orders of magnitude (e.g. “could it be a thousand? A billion? 100 million?”), and that one could be out by a multiple or order of magnitude rather than a particular value (compare to the previous approach - it is much less natural to think you should be unsure about how many digits one should write down). $1\cdot {10}^{6\pm 2}$ would include the true value of 25 million.

Odds are odds are better than probabilities for small chances

Although there are some reasons (especially for Bayesians) to prefer odds to probability in general, reasons parallel to the above recommend them for weighing up small chances - especially sub-percentile chances. I suspect two pitfalls:

1. Translating appropriate levels of uncertainty is easier: more natural to contemplating adding zeros to the denominator of 1/x than adding zeros after the decimal for 0.x.
2. Percentages are not that useful notation for sub-percentile figures (e.g. 0.001% might make one wonder whether the ‘%’ is a typo). Using percentages for probabilities ‘by reflex’ risks anchoring one to the [1%, 99%] range (“well, it’s not impossible, so it can’t be 0%, but it is very unlikely...”)

Also similar to the above, although people especially suck with rare events, I think they may suck less if they develop the habit of at least cross-checking with odds. As a modest claim, I think people can at least discriminate 1 in 1000 versus 1 in 500000 better than 0.1% and 0.002%. There is expression in the ratio scale of odds that the absolute scale of probability compresses out.

The ‘have you tried fractions?’ solution to inter-theoretic value comparison

Consider this example from an Open Philanthropy report [h/t Ben Pace]:

The “animal-inclusive” vs. “human-centric” divide could be interpreted as being about a form of “normative uncertainty”: uncertainty between two different views of morality. It’s not entirely clear how to create a single “common metric” for adjudicating between two views. Consider:

Comparison method A: say that “a human life improved” is the main metric valued by the human-centric worldview, and that “a chicken life improved” is worth >1% of these (animal-inclusive view) or 0 of these (human-centric view). In this case, a >10% probability on the animal-inclusive view would lead chickens to be valued >0.1% as much as humans, which would likely imply a great deal of resources devoted to animal welfare relative to near-term human-focused causes.

Comparison method B: say that “a chicken life improved” is the main metric valued by the animal-inclusive worldview, and that “a human life improved” is worth <100 of these (animal-inclusive view) or an astronomical number of these (human-centric view). In this case, a >10% probability on the human-inclusive view would be effectively similar to a 100% probability on the human-centric view.

These methods have essentially opposite practical implications.

There is a typical two-envelopes style problem here (q.v. Tomasik): if you take the ‘human value’ or ‘chicken value’ envelope first, method A and method B (respectively) recommend switching despite saying roughly the same thing. But something else is also going on. Although method A and method B have similar verbal descriptions, their mathematical sketches imply very different framings of the problem.

Consider the trade ratio of chicken value: human value. Method A uses percentages, which implies we we are working in absolute values, and something like the real number line should be the x axis for our distribution. Using this as the x-axis also suggests our uncertainty should be distributed non-crazily across it: the probability density is not going up or down by multiples of zillions as we traverse it, and 0.12 is more salient than ${10}^{-7}$. It could look something like this:

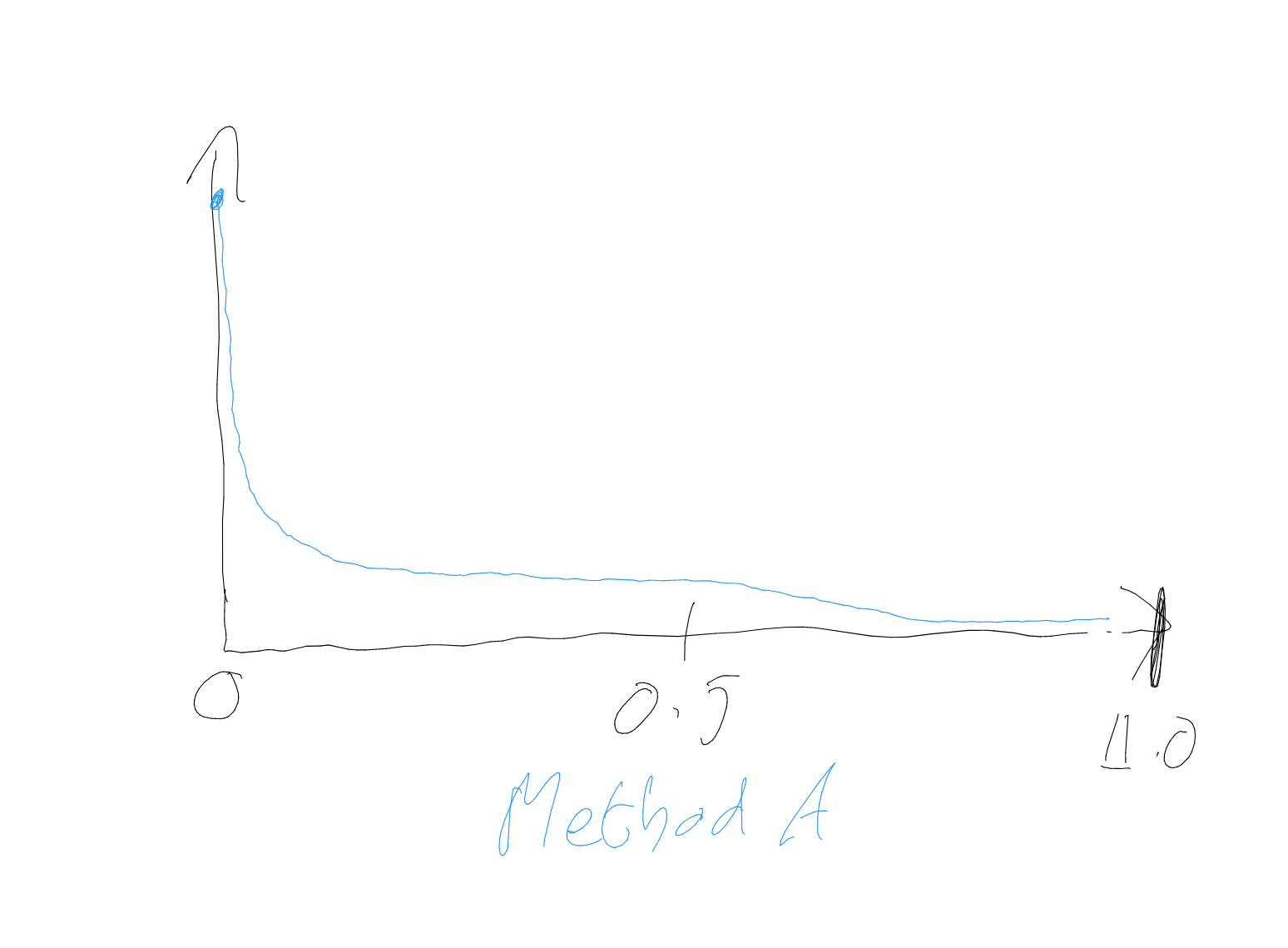
By contrast, method B uses a ratio - furthermore a potentially astronomical ratio. It suggests the x-axis has to be on something like a ${10}^{-x}$ scale (roughly unbounded below, although it does rule out zero or ${10}^{-\infty }$ - it is an astronomical ratio, not an infinite one). This axis, alongside the intuition the distribution should not look crazy, suggests our uncertainty should be smeared over orders of magnitude. ${10}^{-6}$ is salient, whilst $1.2\cdot {10}^{-1}$ is not. It could look something like:

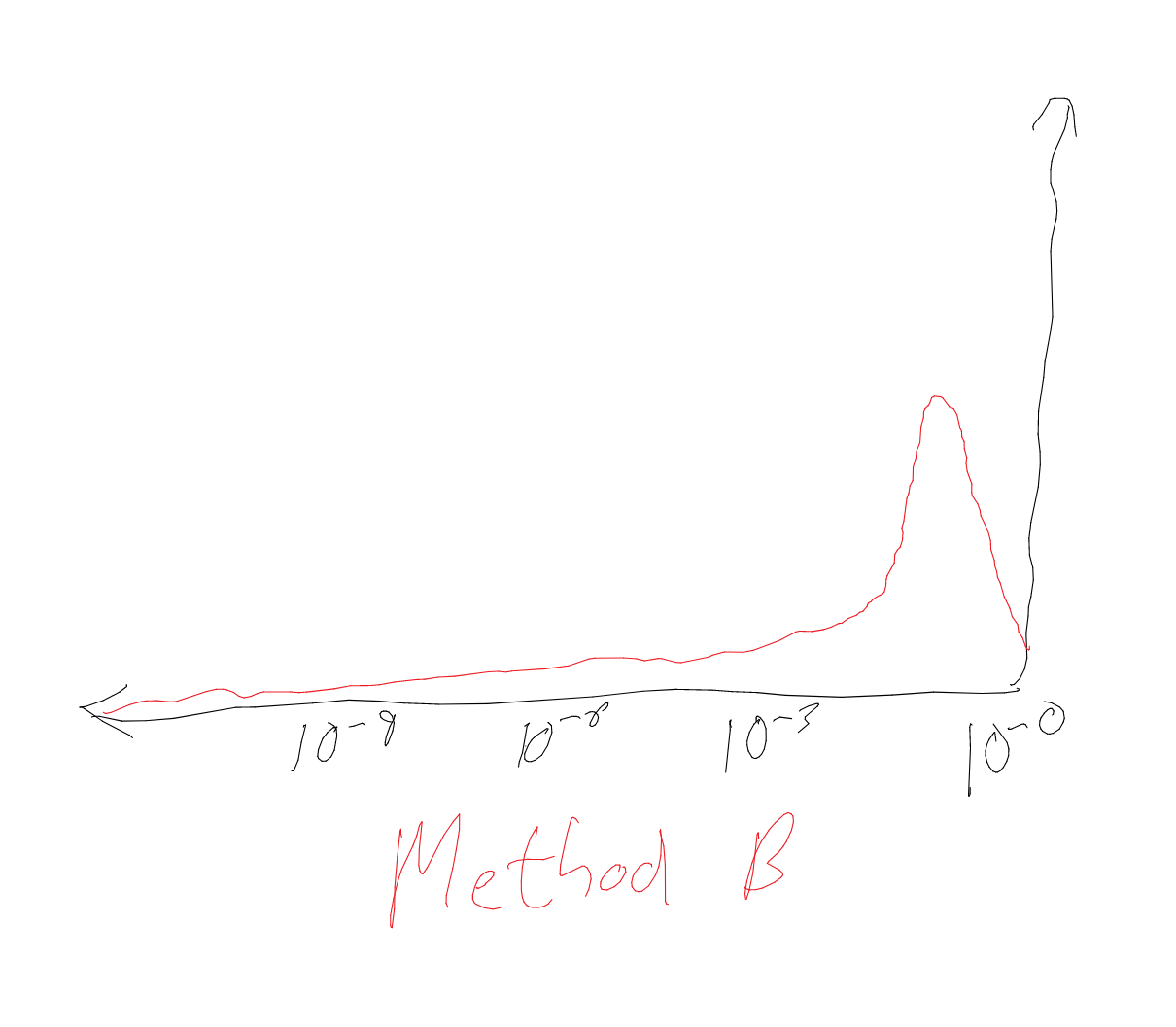
Yet these intuitive responses do look very crazy if plotted against one another on a shared axis. On method A’s implied scale, method B naturally leads us to concentrate a lot of probability density into tiny intervals near zero - e.g. much higher density at the pixel next to the origin ($<{10}^{-3}$) than ranges like [0.2, 0.3]. On method B’s implied scale, method A places infinite density infinitely far along the axis, virtually no probability mass on most of the range, and a lot of mass towards the top (e.g much more between $2\cdot {10}^{-1}$ and $3\cdot {10}^{-3}$ than ${10}^{-3}$ and ${10}^{-9}$):

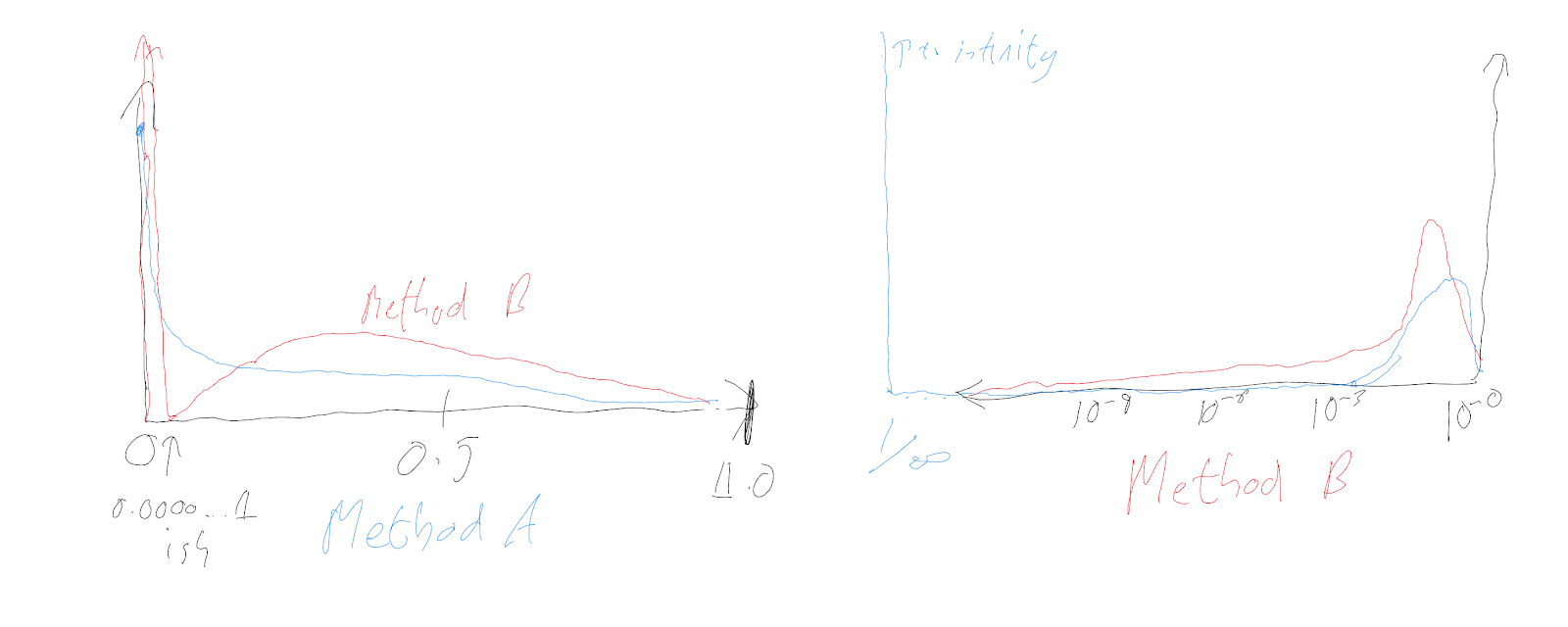
Which one is better? I think most will find method A’s framing leads them to more intuitive results on reflection. Contra method B, we think there is some chance chickens have zero value (so humans count ‘infinitely more’ as a ratio), and we think there’s essentially no chance of them being between (say) a billionth and a trillionth of a human, where they would ‘only’ count astronomically more. In this case, method B’s framing of an unbounded ratio both misleads our intuitive assignment, and its facially similar description to method A conceals the stark differences between them.

Conclusions

It would be good to have principles to guide us, beyond collecting particular examples. Perhaps:

1. One can get clues for which notation to use from one’s impression of the distribution (or generator). If the quantity results from multiplying (rather than adding) a lot of things together, you’re probably working on a log scale.
2. If one is not sure, one can compare and contrast by mentally converting into equivalent notation. One can then cross-check these against ones initial intuition to see which is a better fit.

Perhaps all this is belabouring the obvious, as all of this arises as pedestrian corollaries from other ideas in and around EA-land. We often talk about heavy-tailed distributions, managing uncertainty, the risk of inadvertently misleading with information, and so on. Yet despite being acquainted with all this since medical school, developing these particular habits of mind only struck me in the late-middle-age of my youth. By the principle of mediocrity - despite being exceptionally mediocre - I suspect I am not alone.