June 4, 2017
Below is an article based on a transcript of "The Moral Value of Information", a popular 2017 talk by the NYU philosopher Amanda Askell. She argues that we often underestimate the value of new information or knowledge when thinking of how to do good.
The Moral Value of Information
In this article I'm going to start with making two claims. The first claim is that we generally prefer interventions with more evidential support, all else being equal. I hope you find that claim plausible and I’ll go into detail later about what it means. The second claim I’m going to argue for is that having less evidence in favor of a given intervention means that your credences about the effectiveness of that intervention are what I call “low resilience”.
This second claim has been explored in decision theory to some extent. It holds even if your credences about the effectiveness of that intervention are the same value. So, if I thought there was a 50% chance that I would get $100, there’s a difference between a low resilience 50% and a high resilience 50%.
I’m going to argue that, if your credences in a particular domain are low resilience, then the value of information in this domain is generally higher than it would be in a domain where your credences are high resilience. And, I’m going to argue that this means in many cases, we should prefer interventions with less evidential support, all else being equal. Hopefully, you’ll find that conclusion counterintuitive and interesting.
The first thing to say is that we generally think that expected value calculations are a good way of estimating the effectiveness of a given intervention. For example, lets imagine that there are two diseases: (very novelly named) Disease A and Disease B [Figure 1].
Say these two diseases are virtually impossible to differentiate. They both have the same symptoms, and they cause the same reduction in life expectancy, etc. Their key difference is that they respond very differently to different treatments, so any doctor who finds themselves with a patient with one of these conditions is in a difficult situation.

They can prescribe Drug A which costs $100. If the patient has Disease A, then Drug A will extend their life by another 10 years. If on the other hand the patient had Disease B, it won’t extend their life at all. They will die of Disease B, because Disease B is completely non-responsive to Drug A. Therefore, the expected years of life that we get from Drug A is 0.05 per dollar. Drug B works in a very similar way, except it is used to treat Disease B. If you have Disease A, it will be completely non-responsive. So, it’s got the same expected value as Drug A.
Then, we have Drug C, which also costs $100. Both Disease A or Disease B are somewhat responsive to Drug C so this is a new and interesting drug. From Figure 1 we can see the expected value for Drug C is greater than the expected value for either Drug A or Drug B. So we think, “Okay, great. Kind of obvious we should prescribe Drug C.”
Suppose that Drug A and Drug B have been already heavily tested in numerous trials, and they’ve been shown in meta-analyses to be highly effective, and that the estimates in Figure 1 are extremely robust. Drug C on the hand, is completely new. It’s only had a single trial, in which it increased patients’ lives by many years. We assume that this was in a trial of patients with both diseases.
Say you have a conservative prior about the effectiveness of a drug; you think “In likelihood, most random drugs that we were to select would either be net neutral or net negative”. If you see one trial in which a drug massively extends someone’s life, then your prior might bring you down to something like six years, regardless of whether they have Disease A or Disease B. We have the same expectation for Drug C as before, but suddenly it seems a bit more questionable whether we should prescribe it.
This idea that we should favor interventions with more evidence, and that expected utility theory can’t capture this, is summed up in this blog post from GiveWell from 2016.
“There seems to be nothing in explicit expected value that penalizes relative ignorance or relatively poorly grounded estimates. If I can literally save a child I see drowning by ruining a $1,000 suit, but in the same moment that I make a wild guess that this $1,000 could save 2 lives if I put it toward medical research, then explicit expected value seems to indicate that I should opt for the latter.”
The idea is that there’s something wrong with expected value calculations because they kind of tell us to take wild guesses, as long as the expected value is higher. I want to argue that there are two claims that we might want to vindicate in these sorts of cases.
The first claim is one that I and hopefully you find quite plausible, and it’s the claim that evidence matters. How much evidence we have about an intervention can make a difference to what we should do.
The second claim is one that I think is implied by the above quote, which is that we should favor more evidence, all else being equal. So, if the expected value of two interventions is similar, we should generally favor investing in interventions that have more evidence supporting them.
Maybe we can say that this is relevantly similar to the case we have with Drugs A, B, and C. In a case where you have a lot of evidence that Drug A and Drug B have the effects as in Figure 1, this might favor giving one of these well known drugs over a new one, such as Drug C, that’s only been shown in one trial to be effective.
I’m going to consider both of these claims, and whether expected value calculations can vindicate either or both of them. As mentioned at the beginning, I’m going to argue that it can support the first claim (that evidence matters) but that it actually rejects the second claim (that we should favor interventions with more evidence, all else being equal).
Let's begin. I want to turn to this notion of resilience, and how we represent how much evidence we have, in terms of the credences we assign to propositions such as “This drug will cure this disease.”

See Figure 2. Take Case 1, which is an untested coin. I’ve given you no information about how biased this coin is. It could be completely biased in favor of heads, it could be completely biased in favor of tails, or it could be a completely fair coin. You have no information to distinguish between any of these hypotheses. It seems like, in this case where you have no idea about what the bias of a coin is, if I were to ask you “What is the chance it lands heads on the next throw?”, you’re going to have to reply “It’s about 50%" , because you have no reason to favor a heads bias over a tails bias.
Now consider a difference case, which is Case 2, the well-tested coin. When you flip the well-tested coin you get the following sequence: “Heads, heads, heads, tails, heads, heads, tails, tails,” until the coin has been flipped a million times. You had a very, very boring series of days flipping this coin.
For Case 1, in answer to the question “What’s the probability that the coin will land heads in the next flip?” you should say "0.5 or 50%.” In Case 2, where you tested the coin a lot and it’s come up heads roughly 50% of the time, tails roughly 50% of the time, you should also say that the next flip is 50% likely to be heads.
The difference between the untested coin and the well-tested coin cases is reflected in the resilience levels of your credences. One kind of simple formulation of resilience, the credo-resilience, is how stable you expect your credences to be in response to new evidence. If my credences are high resilience, then there’s more stability. I don’t expect them to vary that much as new evidence comes in, even if the evidence is good and pertinent to the question. If they’re low resilience, then they have low stability. I expect them to change a little in response to new evidence. This is the case with the untested coin, where I have no data about how good it is, so the resilience of my credence of 50% is fairly low.
It’s worth noting that resilience levels can reflect either the set of evidence that you have about a proposition, or your prior about the proposition. For example, if you saw me simply pick the untested coin up out of a stack of otherwise fair coins, you would have evidence that it’s fair. But if you simply live in a world that doesn’t include a lot of very biased coins, then your prior might be doing a lot of the work that your evidence would otherwise do. These are the two things that generate credo-resilience.
In both cases with the coins, your credence that the coin will land heads on the next flip is the same - it’s 0.5. Your credence of 0.5 about the tested coin is resilient, because you’ve done a million trials of this coin. Whereas, your credence about the untested coin is quite fragile. It could easily move in response to new evidence, as we can see in Figure 3.

Take this third case. You start to test the untested coin, so you perform a series of flips with the coin, and you start to see a pattern. In a case like this, it looks like the coin is pretty heavily heads biased, or you at least start to quite rapidly increase your credence that it’s heads biased. As a result, your credence that it’s going to come up heads next time is much higher. Because you had less evidence about the untested coin, your credence of 0.5 in it landing heads was much more fragile, and now your credence changes in response to evidence.
You wouldn't change your credence if you got this sequence of all-heads on the well-tested coin, because more evidence means that your credences are more resilient. If you saw a series of five heads after performing a million trials where it landed heads roughly half the time, this all-heads sequence is just not going to make a huge difference to what you expect the next coin flip to be.
I think credo-resilience has some interesting implications. A lot of people seem to be kind of unwilling to assert probability estimates about whether something is going to work or not. I think a really good explanation for this is that, in cases where we don’t have a lot of evidence, we have low credence in how good our credences are.
In essence, we think it’s very likely that our credences are going to move around a lot in response to new evidence. We’re not willing to assert a credence that we think is simply going to be false or inaccurate as soon as we gain a little bit more evidence. Sometimes people think you have mushy credences, that you don’t actually have precise probabilities that you can assign to claims such as “This intervention is effective to Degree N.” I actually think resilience might be a good way of explaining that away, by instead claiming “No. You can have really precise estimates. You just aren’t willing to assert them.”
This has a huge influence on the value of information, which is the theme of this piece. Our drugs scenario is supposed to be somewhat analogous to different altruistic interventions.
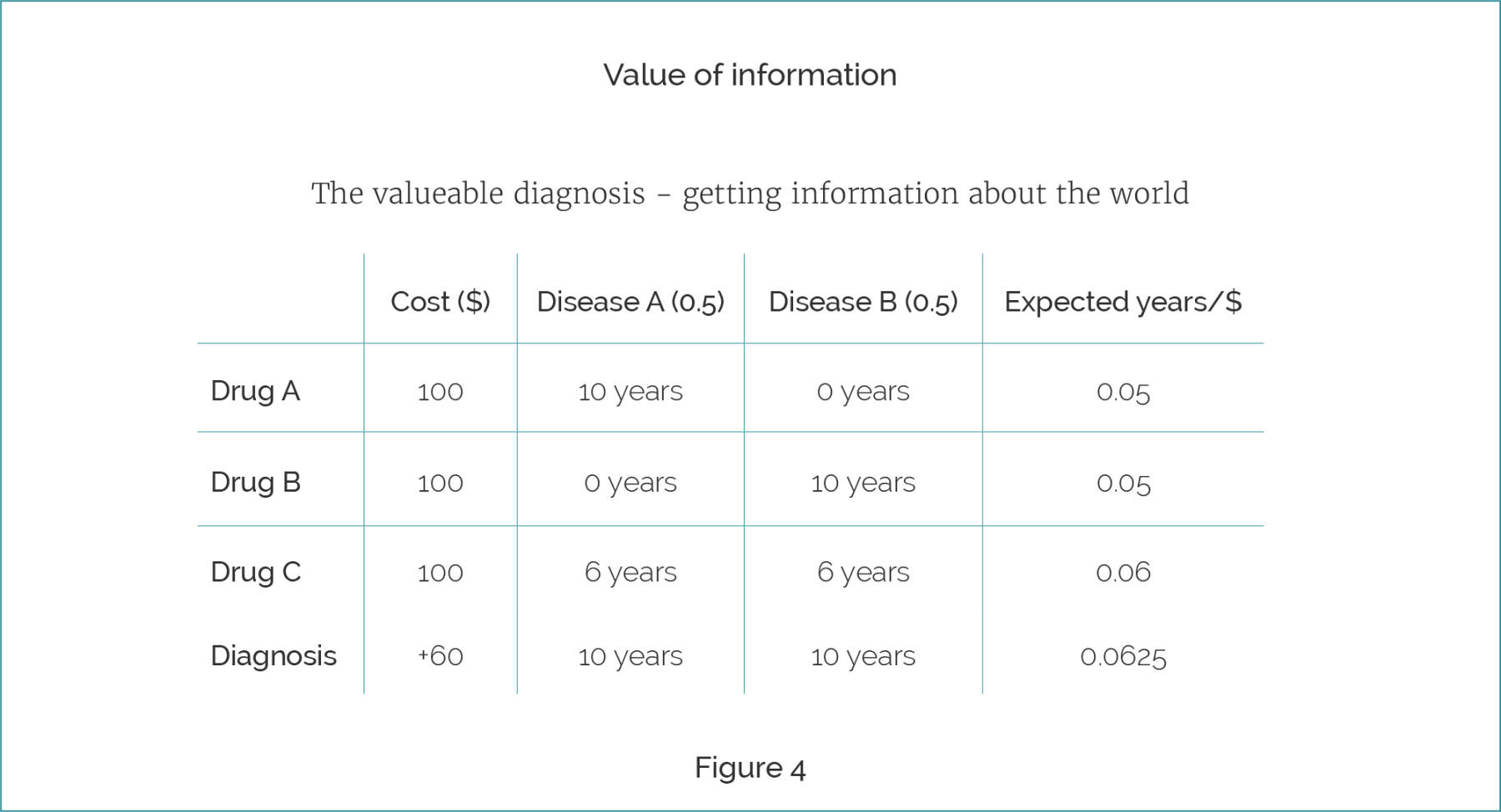
In the original case, we had the following kind of scenario, where we had expected 0.05, 0.05 and 0.06 for the three drugs. Of course, one thing that we can do here is gain valuable evidence about the world. Consider this case, where diagnosis is invented, at least as far as Disease A and Disease B are concerned. So, we can now diagnose whether you have Disease A or Disease B, and it costs 60 additional dollars to do so. Given this, if I diagnose you, then I can expect that conditional on diagnosis, if you have Disease A, you will live for 10 years because, I will be able to then pay an additional $100 to give you Drug A. If you have Disease B, I’ll be able to pay an additional $100 to get you Drug B.
In this case, the value of diagnosis, including the cost of then curing you of the disease, is higher than any of the original interventions. Hopefully it is intuitive that, rather than giving you Drug A, Drug B, Drug C, I should diagnose you and give you the correct drug.
The previous example was concerned with information about the world, which we think is valuable anyway. Now suppose I care about global poverty and I want to discover good interventions. To find out more about the world I could, for example, research deficiencies that exist in India and see if there are good ways to improve them.
A different way we can gain valuable information is by finding out about interventions themselves [Figure 5]. An example would be to look at the actual intervention of Drug C, and how effective it is.
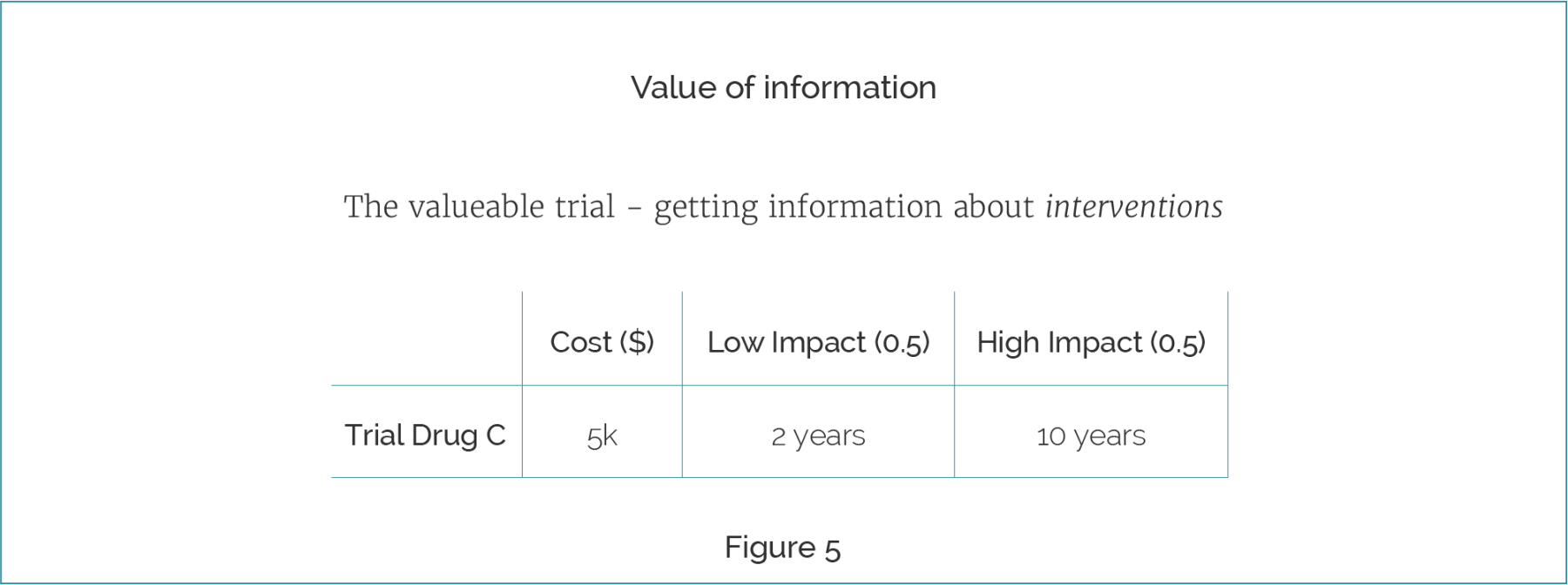
Suppose, in our ideal world that it costs $5000 to run a trial of Drug C that would bring you to certainty about its effectiveness. Suppose, also, that somehow you know it can only be very low impact or very high impact. You have a credence of about 0.5 that the results will show Drug C only extends life by two years in both Disease A and Disease B. This is our skeptical prior. But you also have a credence of about 0.5 that the drug will extend life by 10 years in both cases. We will also assume diagnosis has gone out the window.
Now Imagine the scenario where you are currently prescribing Drug C. You obviously don't exist in any modern medical system, since you're ignoring the fact that there is low evidence here and you're going with the expected value as is. Then the question is, "What is the value of doing a trial of Drug C, especially given that you're already prescribing Drug C?". If your credence of low impact goes to 1 - you suddenly discover that this drug is much less effective than you initially thought - then you're going to switch from Drug C to prescribing Drug A or B again.

The per patient benefit is going to go from two to five years of expected life in this case where you've run the trial. Whereas, if Drug C is a low impact drug and you don't perform the trial, you don't spend the $5000, but you will only get two years of additional life per $100. Every time you see Disease A and Disease B you will continue to prescribe Drug C and it will only give people an additional two years of life. Alternatively, if it is high impact, then you will have been accidentally prescribing something that is very good and providing ten years of additional life.
We can see the trial adds 1.5 years of expected life per future treatment. Therefore, if there are more than 2,000 patients, the value of investing in a trial of Drug C is better than giving any of the drugs currently present. In this case the information value swamps the direct value of intervention here.
The value of investing in trials of Drug A or B is going to be negligible because credences about their effectiveness are already resilient. This builds up to the rather intrusive conclusion that expected value calculations might say that in cases where all else is equal, we should favour investing in interventions that have less evidence, rather than interventions that have more.
This means, if the expected concrete value of two interventions is similar, we should generally favor investing in interventions that have less evidence supporting them. I'm going to use concrete value to mean "Non-informational value". The idea here is that in such scenarios, the concrete values for interventions are the same, but the information value for one of them is much higher, namely the one where you have a much lower resilience credence generating your expected value calculation.
This gets us to the "What does it mean, and what should we do" part. Hopefully I have convinced you that, despite the fact that it was an intuitive proposition that we should favour things with more evidence, there is actually some argument that we should favor things that have less evidence.
When considering information value, there are three options available to us: "Explore, exploit or evade" [Figure 7].

We can choose to explore; and invest resources in interventions primarily for their information value. This means things like research, funding to gather data, and career trials. We can exploit, which means investing resources in an intervention for its concrete value. That means things like large project grants and entire career choices. Or we can evade; we can decide just not to invest in a given intervention - we either invest elsewhere, or completely delay investment.
The main difference between these three options is the reason for action. Take three people. Amy donates $100 to an existential risk charity to protect the future of humanity. She is just exploiting the value and just looks at the direct concrete value of this intervention.
Bella donates $100 to the same charity to find out how much good they can do in the world. She is donating mainly to explore and then later exploit. She'll think to herself: "Let's see how valuable this is" and if it is very valuable, then she will mine the value of it.
Carla donates $100 to the same charity, but for the reason of getting humanity to have more time to discover what the best causes are. She is exploiting the direct value the charity does in reducing existential risk in order to have more time to discover what the best causes are and then exploit those. In essence, she is exploiting to explore to exploit.
When is exploring especially cost effective?
Essentially, when there are three features:
- When there is more uncertainty about the direct value of an intervention. This means options that have high expected value, but low resilience.
- When there are high benefits of certainty about the direct value. We would then be able to repeatedly mine it for value.
- When there are low information costs. This means the information is not too costly to obtain and the delay is low cost (you don't want to be looking for information when cars are driving towards you, as the cost of not taking action and getting out the way is high!).
The question I have is: "Is gaining information especially valuable for effective altruists?". Another way to put it is: "Is information essentially its own cause area, within effective altruism?"
There is a lot of uncertainty within and across good cause areas, particularly if we consider long-term indirect effects. We don't know about the long-term indirect effects of a lot of our interventions.
The benefits of certainty are high as we expect to use this information in the long term. Effective Altruism is a multi-generational project as opposed to a short-term intervention. So, you expect the value of information to be higher, because people can explore for longer and find optimal interventions.
To some degree there are low information costs while the movement is young and there is still a lot of low-hanging fruit. This is with caveats: Maybe you're a bit like Carla and you're very worried that we're screwing up the climate or that nuclear war is going to go terribly wrong. In which case, maybe you think we should be directly intervening in those areas.
What difference would exploring more make to Effective Altruism?
I think we could probably invest a lot more time and resources in interventions that are plausibly good, in order to get more evidence about them. We should probably do more research, although I realise this point is somewhat self-serving. For larger donors, this probably means diversifying their giving more if the value of information diminishes steeply enough, which I think might be the case.
Psychologically, I think we should be a bit more resilient to failure and change. When people consider the idea that they might be giving to cause areas that could turnout to be completely fruitless, I think they find it psychologically difficult. In some ways, just thinking "Look, I'm just exploring this to get the information about how good it its, and if it's bad, I'll just change. Or, if it doesn't do as well as I thought, I'll just change." can be quite comforting if you worry about these things.
The extreme view that you could have is "We should just start investing time and money in interventions with high expected value, but little or no evidential support." A more modest proposal, that I tentatively endorse, is "We should probably start explicitly including the value of information, and assessment of causes and interventions, rather than treating it as an afterthought to concrete value." In my experience, information value can swamp concrete value; and if that is the case, it really shouldn't be an afterthought. Instead it should be one of the primary drivers of values, not an afterthought in your calculation summary.
In summary, evidence does make a difference to expected value calculations via the value of information. If the expected concrete value to interventions is the same, this will favour testing out the intervention with less evidential support, rather than the one with more. Taking value of information seriously would change what effective altruists invest their resources in, be it time or money.

Thanks for doing this, I think it's a great talk.
The images ended up a bit too small, I think. Is it possible to make them larger somehow? I think that would be great. Thanks.
Yep - the author can click on the image and then drag from the corner to enlarge them (found this difficult to find myself)
Thanks for the tip- have now edited!