with $\eta =1/\alpha$.

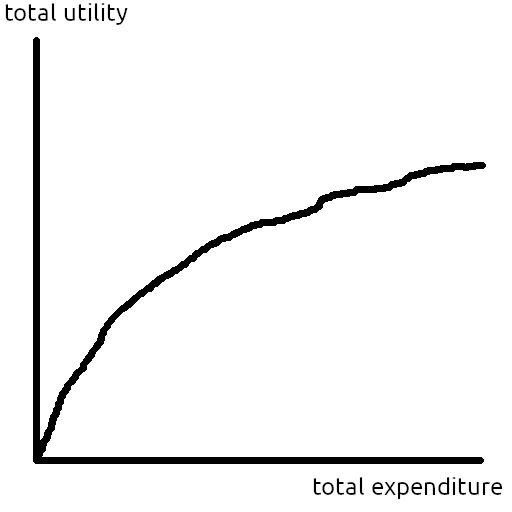
You've probably seen a curve like Figure 1 before: We can do more good by expending more resources, but the marginal cost-effectiveness tends to decrease as we run out of low-hanging fruit. This post is about the relationship between that utility vs. expenditure curve and the set of possible opportunities we can work on.

In 2021, OpenPhil wrote that they model GiveWell's returns to scale as isoelastic with η=0.375. In a recent blogpost, OpenPhil wrote that they "tend to think about returns to grantmaking as logarithmic by default"^[1]. In the model they cite for logarithmic returns, @Owen Cotton-Barratt models opportunities as having independent distributions of cost and benefit and works out approximately logarithmic utility curves from some reasonable assumptions. What follows is a simpler but less general approach to the same problem.

Think of the distribution of opportunities as a density curve with cost-effectiveness on the x axis and available scale at that level of cost-effectiveness on the y axis (see Figure 2). By cost-effectiveness, i mean the utils-per-dollar of an opportunity. And by available scale, i mean how many dollars can be spent at a given level of cost-effectiveness^[2]. Equivalently, you can think of the y axis as the density of ways to spend one dollar at a given cost-effectiveness.

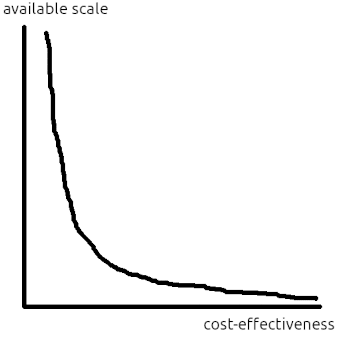
A univariate distribution of opportunities is easier to reason about than a bivariate one, but at the cost of losing information that might affect the order in which we fund them, so we can't represent something like difficulty-based selection in Owen Cotton-Barratt's model.^[3]

Suppose that we start at the positive infinity cost-effectiveness end of the opportunity distribution and work our way left towards zero^[4]. In reality, some low-hanging fruit has already been picked, but that's OK because it just means that in the final answer we shift our position on the utility vs. expenditure graph by however many dollars have already been spent.

Cost-effectiveness is the derivative of utility with respect to expenditure. And available scale density is the derivative of expenditure with respect to cost-effectiveness. Letting $q$ be cost-effectiveness, $S$ be the scale density function, and $U$ be the utility function, we have the following differential equation:

where $U^{\prime }$ is cost-effectiveness as a function of total expenditure, $(U^{\prime }{)}^{-1}$ is total expenditure as a function of cost-effectiveness, and $\left(\right(U^{\prime }{)}^{-1}{)}^{\prime }$ is the derivative of expenditure with respect to cost-effectiveness. Solving this differential equation lets us convert between two different pretty intuitive^[5] ways of thinking about diminishing returns to scale.

I think it makes sense to model the distribution of opportunities as a power law:

• First and foremost, it makes the math easy.
• Rapidly approaching 0 at infinity makes sense.
• Going to infinity at 0 makes sense because there's a kajillion ways to spend a ton of resources inefficiently.
• A lot of stuff actually is pretty Pareto-distributed in real life.
• And, of course, cost-effectiveness of opportunities having a Pareto-like distribution is EA dogma^[6]

And so that the integral converges on the positive infinity side, the exponent must be less than negative one.

It turns out that if you work this out (see appendix) for a power law opportunity distribution $S\left(q\right)=k{q}^p$, you wind up with an isoelastic $U$ where

This seems like a pretty neat and satisfying result that hopefully will make it easier to think about this stuff. I suspect that some EAs have been, like me, explicitly or implicitly modelling the distribution of cost-effectiveness of opportunities as a power law and modelling diminishing returns to scale as isoelastic without thinking about both of those things at the same time and realizing that, when we do interventions in the optimal order, those two things are mathematically equivalent.

appendix

derivation

import sympy as sp

q = sp.symbols("q", positive=True)
eta = sp.symbols("eta", positive=True)
k = sp.symbols("k", positive=True)
S_tot_0 = sp.symbols("S_tot_0", positive=True)

# This needs to be written as -1 - something positive
# to enforce that p is less than -1 so that the integral converges
# and sympy is able to make some necessary simplifications.
# And then i went back and changed that something to 1 / eta
# once i worked out the answer and saw that it was an isoleastic utility function.
p = -1 - 1 / eta

S = k * q**p

q_0 = sp.solve(sp.integrate(S, (q, q, sp.oo)) - S_tot_0, q)[0]

# What we actually want to do here is evaluate this
# integral from q_0 to infinity, but sympy can't handle that.
# So, instead, we use the following trick:
# We know that the integral of f(x) from q_0 to sp.oo
# equals something - F(q_0), so define that something as a variable.
# And utility is a torsor, so adding some constant changes nothing.

C = sp.symbols("C", real=True)
U = sp.simplify(C - sp.integrate(q * S, q).subs({q: q_0}))
U = sp.simplify(sp.integrate(U.diff(S_tot_0), S_tot_0))

order = sp.O(U.args[0][0], S_tot_0).args[0]
assert order.equals(S_tot_0 ** (1 - eta))
assert sp.O(U.args[1][0], S_tot_0).equals(sp.O(sp.log(S_tot_0)))

1. ^{^}

   Logarithmic utility is the special case of isoelastic utility where η=1

2. ^{^}

   Because this is a density, it has weird dimensions: dollars per (utils per dollar)  = dollars squared per util

3. ^{^}

   But the information about the opportunities' cost and benefit is still there: *waves hands* If you zoom in on the scale vs. cost-effectiveness curve — that is, reduce the bin width on the histogram to epsilon — you'll see a bunch of Dirac deltas representing individual discrete interventions whose cost is their integral and whose value is their cost times their cost-effectiveness.

4. ^{^}

   I think there's a case to be made that this assumption is less silly than it sounds: If, in everything here, you replace the words "cost-effectiveness" and "utility" with "expected cost-effectiveness" and "how much good we think we did", then all the math still works out the same and the result still makes sense unless there's learning or bias involved, which would both make things too complicated anyway.

5. ^{^}

   to me, at least

6. ^{^}

   "The top x% of interventions are z times more effective than the median intervention!"