Correction to “The Value of Money Going to Different Groups”

In Toby Ord's "The Value Of Money Going to Different Groups", footnote 9 states: “it isn’t more important to help someone living on $200 per year (at official exchange rates) in a place where PPP is high than someone on the same amount where PPP is low”. 

This isn’t right; $PPP$ (purchasing power parity) doesn’t matter if the elasticity parameter $\eta =1$, but it does matter if $\eta \ne 1$ (so in particular, the estimates in the article for $\eta =2$ are only correct for comparing contexts with equal $PPP$s).

To show this, consider again the utility function:

$u\left(c\right)=\{\begin{array}{cc}\frac{c^{1-\eta }-1}{1-\eta }& \eta \ne 1\\ \ln \left(c\right)& \eta =1\end{array}$

Let A and B be two people with the same income $$X$ living in countries A and B, which have different price levels. Then person A’s consumption $c_A$ is given by $c_A=X/P_A$, and person B’s consumption by $c_B=X/P_B$, where $P_i$ is the price level for each person. This gives $PP{P}_{A/B}=P_A/P_B$.

An illustrative example: $PP{P}_{A/B}=5$ means person B can consume five times person A for the same amount of money. Plotting the utility curves for these two people:

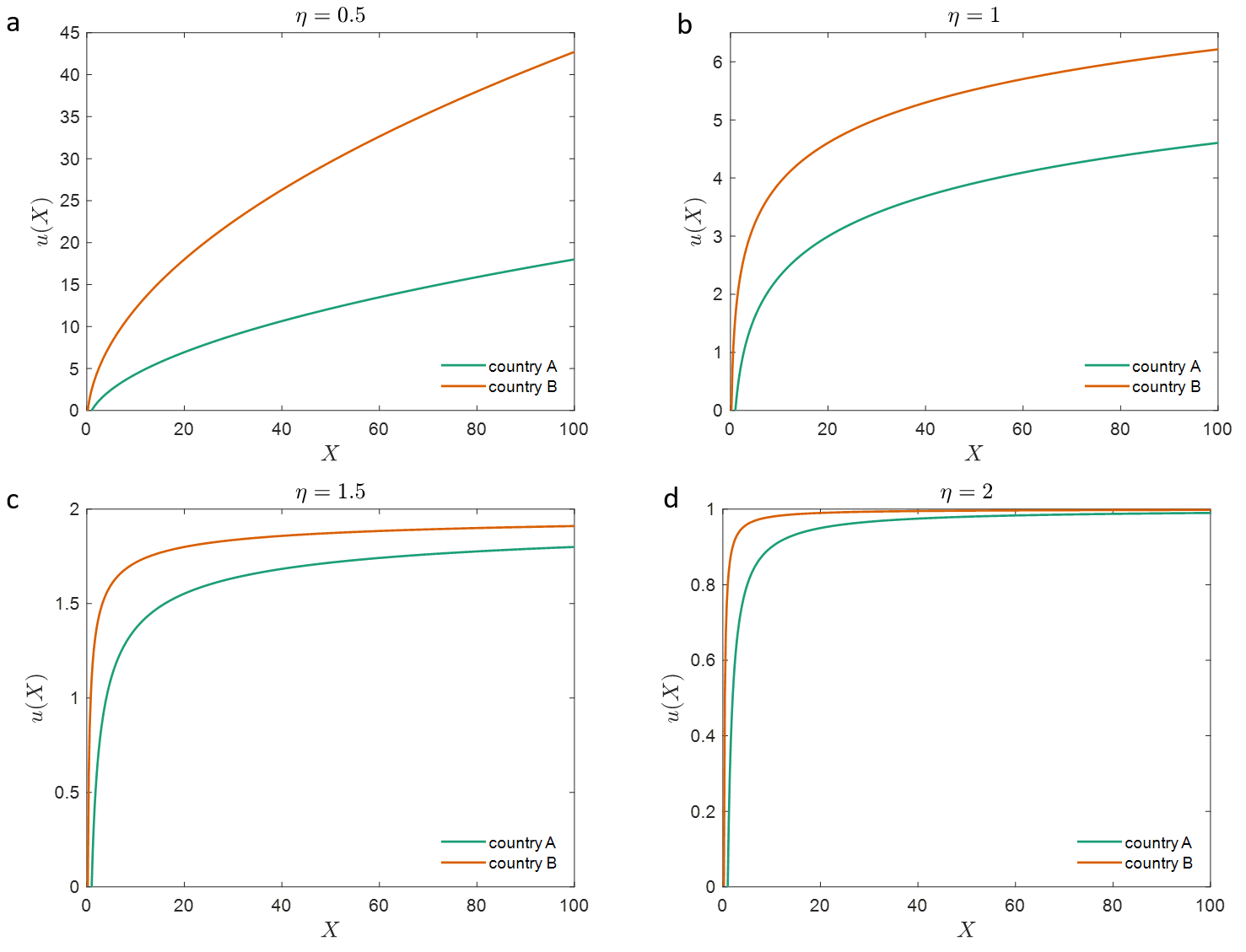
Differentiating the utility function with respect to money, $X$:

$\frac{du}{dX}=\frac{du}{dc}\cdot \frac{dc}{dX}=c^{-\eta }\cdot \frac{1}{P_i}={\left[\frac{X}{P_i}\right]}^{-\eta }\cdot \frac{1}{P_i}=P_i^{\eta -1}{X}^{-\eta }$

where $\frac{du}{dc}$ is the marginal utility of consumption, and $\frac{dc}{dX}$ is the marginal consumption of money.

This differential^[1] shows the two effects of differences in price levels:

(1) Person A on $$X$ in a high price country, will have less consumption and therefore higher marginal utility of consumption, $\frac{du}{dc}$
(2) Person A in the high price country gets less extra consumption for an extra dollar, $\frac{dc}{dX}$

If $\eta =1$, these effects cancel: $\frac{du}{dc}=\frac{X}{P_i}$  and $\frac{dc}{dX}=\frac{1}{P_i}$  so $\frac{du}{dX}=\frac{1}{X}$: gradient is independent of price, $P_i$, for all values of $X$, as shown in Figure 1b. So the claim in footnote 9 is true in this case.

For $\eta \ne 1$ change in utility is proportional to ${P_i}^{\eta -1}$:

If $\eta >1$, point (1) dominates giving person A, with the higher prices, a higher marginal utility (the exponent of $P_i$ is positive, so higher price gives higher marginal utility). See Figure 1c & d.

If $\eta <1$, point (2) dominates giving person B, with the lower prices, a higher marginal utility (the exponent of $P_i$ is negative, so higher price gives lower marginal utility). See Figure 1a.

If it doesn’t seem intuitive that, for two people with the same monetary income, money should go to the person in the country where goods are more expensive, recall that this person has a lower level of consumption. By contrast, consider people with different price values, but the same consumption:

$c=c_A=c_B=c_i=\frac{X_A}{P_A}=\frac{X_B}{P_B}=\frac{X_i}{P_i}$

In this case, the money should always go to the country with a lower price because the $\Delta X$ is scaled to consumption by $P_i$. To show this consider the case $X_{i,2}=X_{i,1}+\Delta X$ for the same initial consumption, described above. See footnote^[1]  for explanation of the following utility change expressions. For $\eta =1$:

$\Delta u=\ln \left(\frac{X_{i,2}}{X_{i,1}}\right)=\ln \left(\frac{X_i+\Delta X}{X_i}\right)=\ln \left(\frac{P_{i}c+\Delta X}{P_{i}c}\right)=\ln \left(\frac{c+X/P}{c}\right)$

And for $\eta \ne 1$:

$\Delta u=P_i^{\eta -1}\frac{{X_{i,2}}^{1-\eta }-{X_{i,1}}^{1-\eta }}{1-\eta }=P_i^{\eta -1}\frac{({X_{i,1}+\Delta X)}^{1-\eta }-{X_{i,1}}^{1-\eta }}{1-\eta }=\frac{{\left(\frac{X_{i,1}+\Delta X}{P_i}\right)}^{1-\eta }-{\left[\frac{X_{i,1}}{P_i}\right]}^{1-\eta }}{1-\eta }=\frac{{(c+\frac{\Delta X}{P_i})}^{1-\eta }-c^{1-\eta }}{1-\eta }$

How does this affect the figures given in the original article? The article’s Table 1 suggests that under the assumption that $\eta =2$, someone living on the mean income in Kenya gets 230x^[2] the marginal utility from a dollar as someone on a median salary in the US. But suppose that goods for someone living on the mean income in Kenya are three times cheaper than in the US, i.e. $PP{P}_{US/K}=3$. Then in fact this multiplier should be 75 (dividing by 3). All the upper bound estimates in the article are over-estimates if $PPP>1$.

1. ^{^}

   Integrating this differential equation between $X_1$ and $X_2$, where $X_2=X_1+\Delta X$ gives two expressions for $\Delta u$ below, independent of price when $\eta =1$ and proportion to $P_i^{\eta -1}$ when $\eta \ne 1$:

   $\Delta u=\{\begin{array}{cc}{P}_i^{\eta -1}\frac{{X_2}^{1-\eta }-{X_1}^{1-\eta }}{1-\eta }& \eta \ne 1\\ \ln \left(\frac{X_2}{X_1}\right)& \eta =1\end{array}$

2. ^{^}

   Should be 220x (rounding error)