Cross-posted to LessWrong. Updated substantially since initial publication.
Overview/purpose of this sequence
While working on an (upcoming) post about a new way to think about moral uncertainty, I unexpectedly discovered that, as best I could tell:
-
There was no single post on LessWrong or the EA Forum that very explicitly (e.g., with concrete examples) overviewed what seem to be the most prominent approaches to making decisions under moral uncertainty (more specifically, those covered in Will MacAskill’s 2014 thesis).[1][2]
-
There was no (easily findable and explicit) write-up of how to handle simultaneous moral and empirical uncertainty. (What I propose is arguably quite obvious, but still seems worth writing up explicitly.)
-
There was no (easily findable and sufficiently thorough) write-up of applying sensitivity analysis and value of information analysis to situations of moral uncertainty.
I therefore decided to write a series of three posts, each of which addressed one of those apparent “gaps”. My primary aim is to synthesise and make accessible various ideas that are currently mostly buried in the philosophical literature, but I also think it’s plausible that some of the ideas in some of the posts (though not this first one) haven’t been explicitly explored before.
I expect that these posts are most easily understood if read in order, but each post should also have value if read in isolation, especially for readers who are already familiar with key ideas from work on moral uncertainty.
Epistemic status (for the whole sequence)
I've now spent several days reading about moral uncertainty, but I wouldn't consider myself an actual expert in this topic or in philosophy more broadly. Thus, while I don't expect this sequence to contain any major, central mistakes, I wouldn’t be surprised if it's inaccurate or unclear/misleading in some places.
I welcome feedback of all kinds (on these posts and in general!).
Moral uncertainty
We are often forced to make decisions under conditions of uncertainty. This uncertainty can be empirical (e.g., what is the likelihood that nuclear war would cause human extinction?) or moral (e.g., does the wellbeing of future generations matter morally?).[3][4] The issue of making decisions under empirical uncertainty has been well-studied, and expected utility theory has emerged as the typical account of how a rational agent should proceed in these situations. The issue of making decisions under moral uncertainty appears to have received less attention (though see this list of relevant papers), despite also being of clear importance.
I'll later publish a post on definitions, types, and sources of moral uncertainty. In the present post, I'll instead aim to convey a sense of what moral uncertainty is through various examples. One example (which I'll return to repeatedly) is the following:
Devon's decision
Suppose Devon assigns a 25% probability to T1, a version of hedonistic utilitarianism in which human “hedons” (a hypothetical unit of pleasure) are worth 10 times more than fish hedons. He also assigns a 75% probability to T2, a different version of hedonistic utilitarianism, which values human hedons just as much as T1 does, but doesn’t value fish hedons at all (i.e., it sees fish experiences as having no moral significance). Suppose also that Devon is choosing whether to buy a fish curry or a tofu curry, and that he’d enjoy the fish curry about twice as much. (Finally, let’s go out on a limb and assume Devon’s humanity.)
According to T1, the choice-worthiness (roughly speaking, the rightness or wrongness of an action) of buying the fish curry is -90 (because it’s assumed to cause 1,000 negative fish hedons, valued as -100, but also 10 human hedons due to Devon’s enjoyment).[5] In contrast, according to T2, the choice-worthiness of buying the fish curry is 10 (because this theory values Devon’s joy as much as T1 does, but doesn’t care about the fish’s experiences). Meanwhile, the choice-worthiness of the tofu curry is 5 according to both theories (because it causes no harm to fish, and Devon would enjoy it half as much as he’d enjoy the fish curry).
The choice-worthiness of each option according to each theory is summarised in the following table:

Given this information, what should Devon do?
"My Favourite Theory"
Multiple approaches to handling moral uncertainty have been proposed. The simplest option is the "My Favourite Theory" (MFT) approach, in which we essentially ignore our moral uncertainty, and just do whatever seems best based on the theory in which one has the highest "credence" (belief). In the above situation, MFT would suggest Devon should buy the fish curry, even though doing so is only somewhat better according to T2 (10 - 5 = 5), and is far worse (5 - -90 = 95) according to another theory in which he has substantial (25%) credence. Indeed, even if Devon had 49% credence in T1 (vs 51% in T2), and the difference in the choice-worthiness of the options was a thousand times as large according to T1 as according to T2, MFT would still ignore the fact the situation is so much "higher stakes" for T1 than T2, refuse to engage in any "moral hedging", and advise Devon proceed with whatever T2 advised.
On top of generating such counterintuitive results, MFT is subject to other quite damning objections (see pages 20-25 of Will MacAskill’s 2014 thesis). Thus, the remainder of this post will focus on other approaches to moral uncertainty, which do allow for "moral hedging".
Types of moral theories
Which approach to moral uncertainty should be used depends in part on what types of moral theories are under consideration by the decision-maker - in particular, whether the theories are cardinally measurable or only ordinally measurable, and, if cardinally measurable, whether or not they’re inter-theoretically comparable.[6]
Cardinality
Essentially, a theory is cardinally measurable if it can tell you not just which outcome is better than which, but also by how much. E.g., it can tell you not just that “X is better than Y which is better than Z”, but also that “X is 10 ‘units’ better than Y, which is 5 ‘units’ better than Z”. (Some readers may be more familiar with distinctions between ordinal, interval, and ratio scales; I'm almost certain "cardinal" scales include both interval and ratio scales.)
My understanding is that popular consequentialist theories are typically cardinal, while popular non-consequentialist theories are typically (or at least more often) ordinal. For example, a Kantian theory may simply tell you that lying is worse than not lying, but not by how much, so you cannot directly weigh that “bad” against the goodness/badness of other actions/outcomes (whereas such comparisons are relatively easy under most forms of utilitarianism).
Intertheoretic comparability
Even if a set of theories are cardinal, they still may not be inter-theoretically comparable. Roughly speaking, two theories are comparable if there's a consistent, non-arbitrary “exchange rate” between the theories' “units of choice-worthiness" (and they're non-comparable if there isn't). MacAskill explains the “problem of intertheoretic comparisons” as follows:
“even when all theories under consideration give sense to the idea of magnitudes of choice-worthiness, we need to be able to compare these magnitudes of choice-worthiness across different theories. But it seems that we can’t always do this. [... Sometimes we don’t know] how can we compare the seriousness of the wrongs, according to these different theories[.] For which theory is there more at stake?”
In his own thesis, Tarsney provides useful examples:
"Consider, for instance, hedonistic and preference utilitarianism, two straightforward maximizing consequentialist theories that agree on every feature of morality, except that hedonistic utilitarianism regards pleasure and pain as the sole non-derivative bearers of moral value while preference utilitarianism regards satisfied and dissatisfied preferences as the sole non-derivative bearers of moral value. Both theories, we may stipulate, have the same cardinal structure. But this structure does not answer the crucial question for expectational reasoning, how the value of a hedon according to hedonic utilitarianism compares to the value of a preference utile according to preference utilitarianism—that is, for an agent who divides her beliefs equally between the two theories and wishes to hedge when they conflict, how much hedonic experience does it take to offset the dissatisfaction of a preference of a given strength (or vice versa)?
Likewise, of course, in trolley problem situations that pit consequentialist and deontological theories against one another, even if we could overcome the apparent structural incompatibility of these rival theories, the thorniest question seems to be: How many net lives must be saved, according to some particular version of consequentialism, to offset the wrongness of killing an innocent person, according to some particular version of deontology?" (line break added)[7]
Three approaches
In MacAskill's thesis, the approaches to moral uncertainty he argues for are:
- Maximising Expected Choice-worthiness (MEC), if all theories under consideration by the decision-maker are cardinal and intertheoretically comparable. (This is arguably the “best” situation to be in, as it is the case in which the most information is being provided by the theories.)
- Variance Voting (VV), a form of what I’ll call “Normalised MEC”, if all theories under consideration are cardinal but not intertheoretically comparable.
- The Borda Rule (BR), if all theories under consideration are ordinal. (This is the situation in which the least information is being provided by the theories.)
- A “Hybrid” procedure, if the theories under consideration differ in whether they’re cardinal or ordinal and/or in whether they’re intertheoretically comparable. (Hybrid procedures will not be discussed in this post; interested readers can refer to pages 117-122 of MacAskill’s thesis.)
I will focus on these approaches (excluding Hybrid procedures), both because these approaches seem to me to be relatively prominent, effective, and intuitive, and because I know less about other approaches. (Potentially promising alternatives include a bargaining-theoretic approach [related presentation slides here], the similar but older and less fleshed-out parliamentary model, and the approaches discussed in Tarsney's thesis.)
Maximising Expected Choice-worthiness (MEC)
MEC is essentially an extension of expected utility theory. MacAskill describes MEC as follows:
“when all [normative/moral] theories [under consideration by the decision-maker] are cardinally measurable and intertheoretically comparable, the appropriateness of an option is given by its expected choice-worthiness, where the expected choice-worthiness (EC) of an option is as follows:
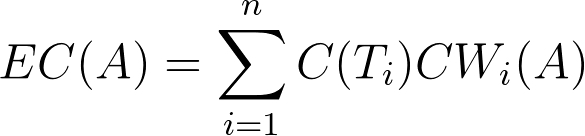
The appropriate options are those with the highest expected choice-worthiness.”
In this formula, C(Ti) represents the decision-maker’s credence (belief) in Ti (some particular moral theory), while CWi(A) represents the “choice-worthiness” (CW) of A (an “option” or action that the decision-maker can take), according to Ti.
To illustrate how MEC works, we will return to the example of Devon deciding whether to buy a fish curry or tofu curry, as summarised in the table of choice-worthiness values from earlier:

(I’ve also modelled this example in Guesstimate. In that link, for comparison purposes, this model is followed by a model of the same basic example using traditional expected utility reasoning, and another using MEC-E (an approach I explain in my next post).)
Using MEC in this situation, the expected choice-worthiness of buying the fish curry is 0.25 * -90 + 0.75 * 10 = -15, and the expected choice-worthiness of buying the tofu curry is 0.25 * 5 + 0.75 * 5 = 5. Thus, Devon should buy the tofu curry.
This is despite Devon believing that T2 is more likely than T1, and T2 claiming that buying the fish curry is better than purchasing the tofu curry. The reason is that, as discussed earlier, there is far “more at stake” for T1 than for T2 in this example.
To me, this seems like a good, intuitive result for MEC, and shows how it improves upon the “My Favourite Theory” approach.
There are two final things I should note about MEC:
-
MEC can be used in exactly the same way when more than two theories are under consideration. (The only reason most examples in this sequence will be ones in which only two moral theories are under consideration is to keep explanations simple.)
-
The basic idea of MEC can also be used as a heuristic, without involving actual numbers.
- For example, say Clara believes that there’s a “high chance” utilitarianism is correct, but that some deontological theory, in which lying is deeply wrong, is “plausible”. Clara is considering whether to tell a lie, and has good reason to believe this will lead to a slight net increase in wellbeing. She might still decide not to lie, despite believing it’s likely that lying is the “right” thing to do, because it’d only be slightly right, whereas it’s plausible it’s deeply wrong.
Another example of applying MEC (which is probably only worth reading if the approach still seems unclear to you) can be found in the following footnote.[8]
Normalised MEC and Variance Voting
(It's possible I've made mistakes in this section; if you think I have, please let me know.)
But what about when, despite being cardinal, the theories you have credence in are not intertheoretically comparable? (Recall that this essentially means that there's no consistent, non-arbitrary “exchange rate” between the theories' “units of choice-worthiness".)
MacAskill argues that, in such situations, one must first "normalise" the theories in some way (which basically means "adjusting values measured on different scales to a notionally common scale"). MEC can then be applied just as we saw earlier, but now with the new, normalised choice-worthiness scores.
There are multiple ways one could normalise the theories under consideration (e.g., by range), but MacAskill argues for normalising by variance. That is, he argues that we should:
“[treat] the average of the squared differences in choice-worthiness from the mean choice-worthiness as the same across all theories. Intuitively, the variance is a measure of how spread out choice-worthiness is over different options; normalising at variance is the same as normalising at the difference between the mean choice-worthiness and one standard deviation from the mean choice-worthiness.”
MacAskill uses the term Variance Voting to refer to this process of first normalising by variance and then using the MEC approach.
(Unfortunately, as far as I could tell, none of the three theses/papers I read that referred to normalising moral theories by variance actually provided a clear, worked example. I've attempted to construct such a worked example based on an extension of the scenario with Devon deciding what meal to buy; that can be found here, and here is a simpler and I think effectively identical method, suggested in a private message.)
In arguing for Variance Voting over its alternatives, MacAskill states that the basic principle normalisation aims to capture is the “principle of equal say: the idea, stated imprecisely for now, that we want to give equally likely moral theories equal weight when considering what it’s appropriate to do” (emphasis in original). He further writes:
“To see a specific case of how this could go awry, consider average and total utilitarianism, and assume that they are indeed incomparable. And suppose that, in order to take an expectation over those theories, we choose to treat them as agreeing on the choice-worthiness ordering of options concerning worlds with only one person in them. If we do this, then, for almost all decisions about population ethics, the appropriate action will be in line with what total utilitarianism regards as most choiceworthy because, for almost all decisions, the stakes are huge for total utilitarianism, but not very large for average utilitarianism. So it seems that, if we treat the theories in this way, we are being partisan to total utilitarianism.
In contrast, if we chose to treat the two theories as agreeing on the choice-worthiness differences between options with worlds involving 10^100 people then, for almost all real-world decisions, what it’s appropriate to do will be the same as what average utilitarianism regards as most choice-worthy. This is because we’re representing average utilitarianism as claiming that, for almost all decisions, the stakes are much higher than for total utilitarianism. In which case, it seems that we are being partisan to average utilitarianism, whereas what we want is to have a way of normalising such that each theory gets equal influence.” (line break added)
(Note that it’s not a problem for one theory to have much more influence on decisions due to higher credence in that theory. The principle of equal say is only violated if additional influence is unrelated to additional credence in a theory, and instead has to do with what are basically arbitrary/accidental choices about exchange rates between units of choice-worthiness.)
MacAskill (pages 110-116) provides two arguments that VV is the approach that satisfies the principle of equal say, and Owen Cotton-Barratt similarly argues for the superiority of normalisation by variance over alternative normalisations. (But note that this approach does seem to have its flaws, as discussed in, e.g., pages 222-223 of Tarsney's thesis.)
The Borda Rule (BR)
Finally, what about when all moral theories under consideration are only ordinal, rather than cardinal (i.e., they say only whether each option is more, equally, or less choice-worthy than each other option, but not by how much)? For such cases, MacAskill recommends a voting method called the Borda Rule (BR; also known as a "Borda count"), with "moral theories play[ing] the part of voters and practical options the part of candidates" (Tarsney). I will first quote MacAskill’s formal explanation of BR (which may be somewhat confusing by itself), before quoting an example he gives and showing what applying BR to that looks like:
“An option A’s Borda Score, for any theory Ti, is equal to the number of options within the option-set that are less choice-worthy than A according to theory Ti’s choice-worthiness function, minus the number of options within the option-set that are more choice-worthy than A according to Ti’s choice-worthiness function.[9]
An option A’s Credence-Weighted Borda Score is the sum, for all theories Ti, of the Borda Score of A according to theory Ti multiplied by the credence that the decision-maker has in theory Ti.
[The Borda Rule states that an] option A is more appropriate than an option B iff [if and only if] A has a higher Credence-Weighted Borda Score than B; A is equally as appropriate as B iff A and B have an equal Credence-Weighted Borda Score.”
I will now show, following MacAskill, how this rule applies to an example he gives in his thesis:
“Julia is a judge who is about to pass a verdict on whether Smith is guilty for murder. She is very confident that Smith is innocent. There is a crowd outside, who are desperate to see Smith convicted. Julia has three options:
[G]: Pass a verdict of ‘guilty’.
[R]: Call for a retrial.
[I]: Pass a verdict of ‘innocent’.
Julia knows that the crowd will riot if Smith is found innocent, causing mayhem on the streets and the deaths of several people. If she calls for a retrial, she knows that he will be found innocent at a later date, and that it is much less likely that the crowd will riot at that later date. If she declares Smith guilty, the crowd will be appeased and go home peacefully. She has credence in three moral theories:
35% credence in a variant of utilitarianism, according to which [G≻R≻I].
34% credence in a variant of common sense, according to which [R≻I≻G].
31% credence in a deontological theory, according to which [I≻R≻G].”
The options’ Borda Scores according to each theory, and their Credence-Weighted Borda Scores, are therefore as shown in the following table:

(For example, G has a score of 2 - 0 = 2 according to utilitarianism because that theory views two options as less choice-worthy than G, and 0 options as more choice-worthy than G.)
The calculations that provided the Credence-Weighted Borda Scores shown in the above table are as follows:
G: 0.35 * 2 + 0.34 * -2 + 0.31 * -2 = -0.6 (this because the utilitarian, common sense, and deontological theories are given credences of 35%, 34%, and 31%, respectively, and these serve as the weightings for the Borda Scores these theories provide)
R: 0.35 * 0 + 0.34 * 2 + 0.31 * 0 = 0.68
I: 0.35 * -2 + 0.34 * 0 + 0.31 * 2 = -0.08
BR would therefore claim that Julia should call for a retrial. This is the case even though passing a guilty verdict was seen as best by Julia’s “favourite theory” (the variant of utilitarianism). Essentially, calling for a retrial is preferred because both passing a guilty verdict and passing an innocent verdict were seen as least preferred by some theory Julia has substantial credence in, whereas calling for a retrial is not least preferred by any theory.
MacAskill notes that preferring this sort of a compromise option in a case like this seems intuitively right. He also argues that alternatives to BR fail to give us the sort of answers we’d want in these or other sorts of cases. (Though Tarsney raises some objections to BR which I won't get into.)
Closing remarks
I hope you have found this post a useful, clear summary of key ideas around what moral uncertainty is, why it matters, and how to make decisions when morally uncertain. Personally, I believe that an understanding of moral uncertainty - particularly a sort of heuristic version of MEC - has usefully enriched my thinking, and influenced some of the biggest decisions I’ve made over the last year.[10]
In my next post, I discuss (possibly novel, arguably obvious) extensions of each of the three approaches discussed here, in order to allow for modelling both moral and empirical uncertainty, explicitly and simultaneously. The post after that will discuss how we can combine the approaches in the first two posts with sensitivity analysis and value of information analysis.[11][12]
I genuinely mean no disrespect to the several posts on moral uncertainty I did discover (e.g., here, here, and here). All did meet some of those criteria, and I’d say most were well-written but just weren’t highly explicit (e.g., didn’t include enough concrete examples), and/or didn’t cover (in the one post) each of the prominent approaches and the related ideas necessary to understand them. ↩︎
Other terms/concepts that are sometimes used and are similar to “moral uncertainty” are normative, axiological, and value uncertainty. See these two posts for info on the overlaps and distinction between these terms. In this sequence, I’ll use “moral uncertainty” in a general sense that also incorporates axiological and value uncertainty, and at least a large part of normative uncertainty.
Also, throughout this sequence, I will use the term "approach" in a way that I believe aligns with MacAskill's use of the term "metanormative theory". ↩︎
It seems to me that there are many cases where it’s not entirely clear whether the uncertainty is empirical or moral. For example, I might wonder “Are fish conscious?”, which seems on the face of it an empirical question. However, I might not yet know precisely what I mean by “conscious”, and only really want to know whether fish are “conscious in a sense I would morally care about”. In this case, the seemingly empirical question becomes hard to disentangle from the (seemingly moral) question “What forms of consciousness are morally important?”
(Furthermore, my answers to that question in turn may be influenced by empirical discoveries. For example, I may initially believe avoidance of painful stimuli demonstrates consciousness in a morally relevant sense, but then change that belief after learning that this behaviour can be displayed in a stimulus-response way by certain extremely simple organisms.)
In such cases, I believe the approach suggested in the next post of this series will still work well, as that approach does not really require empirical and moral uncertainty to be treated fundamentally differently. (Another approach, which presents itself differently but I think is basically the same in effect, is to consider uncertainty over “worldviews”, with those worldviews combining moral and empirical claims.) ↩︎
In various places in this sequence, I will use language that may appear to endorse or presume moral realism (e.g., referring to “moral information” or to probability of a particular moral theory being “true”). But this is essentially just for convenience; I intend this sequence to be neutral on the matter of moral realism vs antirealism, and I believe this post can be useful in mostly similar ways regardless of one’s position on that matter. I discuss the matter of "moral uncertainty for antirealists" in more detail in this separate post. ↩︎
The matter of how to actually assign “units” or “magnitudes” of choice-worthiness to different options, and what these things would even mean, is complex, and I won’t really get into it in this sequence. ↩︎
Christian Tarsney's 2017 thesis thesis (e.g., pages 175-176) explains other ways the "structure" of moral theories can differ, and potential implications of these other differences. These were among the juicy complexities I had to resist cramming in this originally-intended-as-bitesized post (but I may write another post about Tarsney's ideas later; please let me know if you think that'd be worthwhile). ↩︎
It's worth noting that similar issues have received attention from, and are relevant to, other fields as well. For example, MacAskill writes: "A similar problem arises in the study of social welfare in economics: it is desirable to be able to compare the strength of preferences of different people, but even if you represent preferences by cardinally measurable utility functions you need more information to make them comparable." Thus, concepts and findings from those fields could illuminate this matter, and vice versa. ↩︎
Suppose Alice assigns a 60% probability to hedonistic utilitarianism (HU) being true and a 40% probability to preference utilitarianism (PU) being true. Suppose also that Bob wants to play video games, but would actually get slightly more joy out of a day at the beach. Thus, according to HU, letting Bob play video games has a CW of 5, and taking him to the beach has a CW of 6; while according to PU, letting Bob play video games has a CW of 15, and taking him to the beach has a CW of -20.
Under these conditions, the expected choice-worthiness of letting Bob play video games is 0.6 * 5 + 0.4 * 15 = 9, and the expected choice-worthiness of taking Bob to the beach is 0.6 * 6 + 0.4 * -20 = -4.4. Therefore, Alice should let Bob play video games.
Analogously to the situation with the Devon example, this is despite Alice believing HU is more likely than PU, and despite HU positing that taking Bob to the beach being better than letting him play video games. As before, the reason is that there is “more at stake” in this decision for the less-believed theory than for the more-believed theory; HU considers there to only be a very small difference between the choice-worthiness of the options, while PU considers there to be a large difference. ↩︎
MacAskill later notes that a simpler method (which doesn’t subtract the number of options that are more choice-worthy) can be used when there are no ties. His calculations for the example I quote and work through in this post use that simpler method. But in this post, I’ll stick to the method MacAskill describes in this quote (which is guaranteed to give the same final answer in this example anyway). ↩︎
However, these concepts are of course not an instant fix or cure-all. In a (readable and interesting) 2019 paper, MacAskill writes “so far, the implications for practical ethics have been drawn too simplistically [by some philosophers.] First, the implications of moral uncertainty for normative ethics are far more wide-ranging than has been noted so far. Second, one can't straightforwardly argue from moral uncertainty to particular conclusions in practical ethics, both because of ‘interaction’ effects between moral issues, and because of the variety of different possible intertheoretic comparisons that one can reasonably endorse.”
For a personal example, a heuristic version of MEC still leaves me unsure whether I should move from being a vegetarian-flirting-with-veganism to a strict vegan, or even whether I should spend much time making that decision, because that might trade off to some extent with time and money I could put towards longtermist efforts (which seem more choice-worthy according to other moral theories I have some credence in). I suspect any quantitative modelling simple enough to be done in a reasonable amount of time would still leave me unsure.
That said, I, like MacAskill (in the same paper), “do believe, however, that consideration of moral uncertainty should have major impacts for how practical ethics is conducted. [...] It would be surprising if the conclusions [of approaches taking moral uncertainty into account] were the same as those that practical ethicists typically draw.”
In particular, I’d note that considering moral uncertainty can reveal some “low-hanging fruit”: some “trades” between moral theories that are relatively clearly advantageous, due to large differences in the “stakes” different moral theories see the situation as having. (Personally, cases of apparent low-hanging fruit of this kind have included becoming at least vegetarian, switching my career aims to longtermist ones, and yet engaging in global-poverty-related movement-building when an unusual opportunity arose and it wouldn’t take up too much of my time.) ↩︎
To foreshadow: Basically, my idea is that, once you’ve made explicit your degree of belief in various moral theories and how good/bad outcomes appear to each of those theories, you can work out which updates to your beliefs in moral theories or to your understandings of those moral theories are most likely to change your decisions, and thus which “moral learning” to prioritise and how much resources to expend on it. ↩︎
I’m also considering later adding posts on:
- Various definitions, types, and sources of moral uncertainty (drawing in part on these posts).
- The idea of ignoring even very high credence in nihilism, because it’s never decision-relevant.
- Whether it could make sense to give moral realism disproportionate (compared to antirealism) influence over our decisions, based on the idea that realism might view there as “more at stake” than antirealism does.
I’d be interested in hearing whether people think those threads are likely to be worth pursuing. ↩︎

Will's book, 'Moral Uncertainty', is coming out next month for those who are interested in the topic: https://www.amazon.co.uk/Moral-Uncertainty-William-MacAskill/dp/0198722273
As I hope for this to remain a useful, accessible summary of these ideas, I've made various edits as I've learned more and gotten feedback (including on LessWrong), and expect to continue to do so. So please keep the feedback coming, so I can make this more useful for people!
(In the interest of over-the-top transparency, here's the version from when this was first published.)
Hey, thank you very much for the summary!
I have two questions:
(1) how should one select which moral theories to use in ones evaluation of the expected choice worthiness of a given action?
"All" seems impossible, supposing the set of moral theories is indeed infinite; "whatever you like" seems to justify basically any act by just selecting or inventing the right subset of moral theories; "take the popular ones" seems very limited (admittedly, I dont have an argument against that option, but is there a positive one for it?)
(2) how should one assign probabilities to moral theories?
I realise that these are probably still controversial issues in philosophy, so I dont expect a solution. Rather, any (yet speculative) ideas on how to resolve them would be great!
(I'll again just provide some thoughts rather than actual, direct answers.)
Here I'd again say that I think an analogous question can be asked in the empirical context, and I think it's decently thorny in that context too. In practice, I think we often do a decent job of assigning probabilities to many empirical claims. But I don't know if we have a rigorous theoretical understanding of how we do that, or of why that's reasonable, or at least of how to do it in general. (I'm not an expert there, though.)
And I think there are some types of empirical claims where it's pretty hard to say how we should do this.[1] For some examples I discussed in another post:
What process do we use to assign probabilities to these claims? Is it a reasonable process, with good outputs? (I do think we can use a decent process here, as I discuss in that post; I'm just saying it doesn't seem immediately obvious how one does this.)
I do think this is all harder in the moral context, but some of the same basic principles may still apply.
In practice, I think people often do something like arriving at an intuitive sense of the likelihood of the different theories (or maybe how appealing they are). And this in turn may be based on reading, discussion, and reflection. People also sometimes/often update on what other people believe.
I'm not sure if this is how one should do it, but I think it's a common approach, and it's roughly what I've done myself.
[1] People sometimes use terms like Knightian uncertainty, uncertainty as opposed to risk, or deep uncertainty for those sorts of cases. My independent impression is that those terms often imply a sharp binary where reality is more continuous, and it's better to instead talk about degrees of robustness/resilience/trustworthiness of one's probabilities. Very rough sketch: sometimes I might be very confident that there's a 0.2 probability of something, whereas other times my best guess about the probability might be 0.2, but I might be super unsure about that and could easily change my mind given new evidence.
Glad you found the post useful :)
Yeah, I think those are both very thorny and important questions. I'd guess that no one would have amazing answers to them, but that various other EAs would have somewhat better answers than me. So I'll just make a couple quick comments.
I think we could ask an analogous question about how to select which hypotheses about the world/future to use in one's evaluation of the expected value of a given action, or just in evaluating what will happen in future in general. (I.e., in the empirical context, rather than the moral/normative context.)
For example, if I want to predict the expected number of readers of an article, I could think about how many readers it'll get if X happens and how many it'll get if Y happens, and then think about how likely X and Y seem. X and Y could be things like "Some unrelated major news event happens to happen on the day of publication, drawing readers away", or "Some major news event that's somewhat related to the topic of the article happens soon-ish after publication, boosting attention", or "The article is featured in some newsletter/roundup."
But how many hypotheses should I consider? What about pretty unlikely stuff, like Obama mentioning the article on TV? What about really outlandish stuff that we still can't really assign a probability of precisely 0, like a new religion forming with that article as one of its sacred texts?
Now, that response doesn't actually answer the question at all! I don't know how this problem is addressed in the empirical context. But I imagine people have written and thought a bunch about it in that context, and that what they've said could probably be ported over into the moral context.
(It's also possible that the analogy breaks down for some reason I haven't considered.)
There are some fundamental problems facing moral uncertainty that I haven't seen its proponents even refer to, let alone refute:
On your second point, I think it's true that the way I described moral uncertainty in this post applies most straightforwardly if we accept moral realism rather than antirealism. But I think much of the discussion, theories, etc. related to moral uncertainty will still be relevant given various types of moral antirealism - there'll just need to be some adjustments in interpretation and application. (I'm not sure if this is the case for all types of moral antirealism.)
As I say in a footnote of the post:
For more on that, see the post linked to there.
I also don't think it's true that all types of moral antirealism would mean/claim that "words like 'should', 'ought' etc are either necessarily wrong or not even meaningful." And I've talked to thoughtful antirealists who actively argue against such a view - if I recall correctly, this post is a good example of that (and in any case, it's an interesting post).
Hi Arepo,
I'll just respond quickly, but I imagine people who are actively working on moral uncertainty stuff would be able to say much more. And I'll split my response to each point into a separate comment.
On your first point, you may find this paper from Phil Trammell interesting. (Though I haven't read beyond the abstract myself, and am not sure I'd understand the paper easily if I did.) The abstract reads:
I believe similar issues were also discussed on some episodes of the 80,000 Hours Podcast - perhaps one with Hilary Greaves?