Summary

I propose a way to increase contributions to (EA or non-EA) public goods by reducing free-riding incentives, with what I call Mutual Matching. In contrast to traditional donation matching, the mechanism does not require any matching fund.

As an overarching problem, free-riding affects the provision of all sorts of public goods. It occurs when individuals benefit from the efforts of others without sharing the cost, reducing the incentive to contribute. For example, many seem reluctant to donate to global poverty relief if the personal contribution barely changes the lives of the billions in need. Or, one might hesitate to chip in when it’s unlikely to change the housemates’ decision on buying the new TV.

So, people tend to contribute too little, even towards the most pressing problems. To improve on this situation, in Mutual Matching donors automatically co-incentivize each other to give more: each person’s participation increases the sum of donations by a leverage factor of L > 1 times their personal contribution. It is decentralized and scalable and does not require a matching fund. We’ll get to the strings attached in a moment.

The scheme works by asking for conditional donations: each individual donor’s contribution varies with the factor by which it increases the sum donated by all others. As an example, a participant might commit to donating $1 if she’s the only one participating, $7 if her donation ends up increasing others’ summed donations by twice her contribution, and $50 if her contribution increases others by four times hers instead. For all other donors, the idea operates in the same way as for her, although each may choose a higher or lower personal scale of contribution if any.

You may expect an accounting failure, as each person’s individual contribution is supposed to increase the total by more than his own contribution. The magic lies in the organizer, say the charity, proposing consistent voluntary contribution schedules and calculating the feasible equilibrium and individual donations due, as a function of all participants’ commitments and in line with each donors’ causal effect on total contributions. That last part was confusing, right? I promise it is simpler when I explain it in detail below (especially in the three-person example).

Key advantages of Mutual Matching:

• no matching fund required
• scalability to arbitrarily high participant numbers & matching factors (“leverage”)
• each contribution is directly conditional on its verifiable marginal effect on the total sum collected (the explicit relation between this leverage and any contributor’s due donation is also a main distinguishing factor between Mutual Matching and Snowdrift or Rational Street Performer Protocol)
• relative simplicity

A key limitation is that uncertainty about the prospective commitments can limit the leverage factor achievable in practice. Really large factors may be realistic primarily when the scale of aggregate commitments can be well anticipated, maybe because of a well-known pool of donors, or in repeated campaigns.

• This post provides a first overview of the scheme. A more detailed discussion paper is in progress.
• For simplicity, I mainly describe a limited version, in which conditional contribution schedules are the same for all volunteers. I briefly discuss some of the effects of an extension allowing for individual contribution scaling.

This post has been written as part of an EAGeneva fellowship project. I thank Rick van der Ploeg, Aaron Gertler, and especially Naomi Nederlof for valuable comments.

Background

Free-riding in the contribution of public goods (PGs) is an overarching problem, making myriads of EA or non-EA problems difficult to solve. Mutual Matching is a proposition to reduce this market failure in some cases.

Without regulation, PGs are underprovided because individuals have a diminished incentive to contribute: Even if I enjoy the PG, my (non-)contribution will neither increase nor lessen my own enjoyment of it significantly. Most of the impact of my decision is instead borne by others. Even worse, at times my contribution risks crowding out the contributions of others, reducing my eagerness to contribute further—might as well free-ride! This severely affects the support for all sorts of PGs, such as in the domains of poverty relief/development aid, environmental services, existential risk mitigation research, the local communal park, you name it.

Consider the example of poverty relief. In the general population, the majority would find it great if, together, we all spent more to help the poor, yet as individuals, feeling unable to make a significant difference, we choose to do nothing. The apparent success of donation matching can be seen as a direct response to such problems, improving the incentives at least a bit (although whether the donation leverage promise holds through is not always obvious^[1]).

Public policy, such as centralized funding through taxes, could be—and at times is—a more systematic solution. Still, it often remains challenging to agree democratically on an adequate level of support. Preferences are too heterogeneous, and the idea that PGs deserve public policy support seems even challenged on a fundamental level. Raising the required taxes to finance PGs can also be difficult within the international tax competition. Quadratic Funding (from RadicalxChange) theoretically facilitates the democratic determination of the right level of funding of PGs. However, it does not solve the requirement for most of the funding to be provided as public funds.

Mutual Matching aims to help by increasing the incentive for anyone to donate, without a requirement for direct interaction with others or for third-party funding. On a coordination spectrum, the solution is a middle-ground:

1. In systems without coordination, everyone gives unconditionally whatever they want, wholly independent of what others do
2. In systems with full coordination, everyone commits to giving if and only if everyone else gives predefined amounts
3. Mutual Matching falls between these two extremes, where each person commits to giving if their participation causes a certain amount of additional giving by others. More specifically, each person commits to providing an amount that is an (increasing) function of the effect of her donation on the total amount donated by others.

The compromise here can preserve part of the strong incentive of the full-coordination extreme, all while improving robustness, avoiding the strict reliance on everyone to contribute. The amplification of incentives to donate is achieved by a scheme that ensures that any individual donor’s decision to participate causally impacts the sum of contributions from all participants by leverage L times the individual’s donation d, with L ≥ 1 growing in the number of participants.

There exists related literature. Many theoretical and empirical studies focus on the formation of coalitions providing a PG, with contributors assumed to collaborate to agree on ideal choices directly. Here, instead, we avoid the need for direct collaboration among participants.

Some works specifically focus on “matching”. Buchholz et al. 2011 analyze a framework that also aims to increase contribution leverage. But participants therein seem to decide on their contributions neither explicitly based on a known leverage factor (unlike practical matching funds) nor directly conditional on the leverage factor (unlike here).^[2] Related ideas are the Rational Street Performer Protocol (increase donations linearly with the total sum collected) and the mechanism of Snowdrift.coop. The Snowdrift "crowdmatching" platform has the clearest parallels to the idea proposed here. It could be considered a boundary case of Mutual Matching: contributors are donating proportionally to the number of co-donors, but leverage remains constant at 2, so, in contrast to here, there is no increasing bang per buck.

Mechanism

Illustration with three persons

For a basic understanding of Mutual Matching, let’s first consider an example with only three participants and a reduced choice set. In reality, with so few participants, a simple direct negotiation among them might instead often suffice for a reasonable outcome. That said, the scheme might still be helpful even at this scale, avoiding possibly tedious negotiations. 

Each of three persons can decide whether or not to commit to contributing. If a person contributes, the amount d she has to give depends on how many others contribute as well: $10 if she’s the sole contributor, and $15 or $30 if two or all three contribute, as shown in column [1] of Table 1. This progression of the committed per-person contribution, d, is in this example chosen such as to yield a leverage of 1.33 or 2 if two or three people participate (column [4]):

For n = 1, 2, or 3 contributors, the mentioned three individual donation values d yield total donations of n · d = $10, $30, or $90. This means if two decide to contribute, the total sum of donations increases by $30-$10 = $20 relative to the case if only one had contributed. In other words, for each of the two contributors, the personal contribution of $15 has increased the total donated by $20, implying a leverage of $20/$15 = 1.33. Analogously, for the situation with three contributors, the comparison with only two contributors shows that any given individual’s decision to participate has increased the sum collected by $60: from $30 (= 2 · $15) to $90 (= 3 · $30). The leverage of any individual participant in the outcome with three participants has thus been $60/$30 = 2. In other words, anyone’s individual decision to contribute has in this outcome increased the sum collected by twice the individual’s contribution. As a sufficient condition, it is in the interest of an individual to commit to contributing if she is happy to donate at least $10 for a leverage of 1 (only she contributes), at least $15 given a leverage of 1.33, and $30 given a leverage of 2.

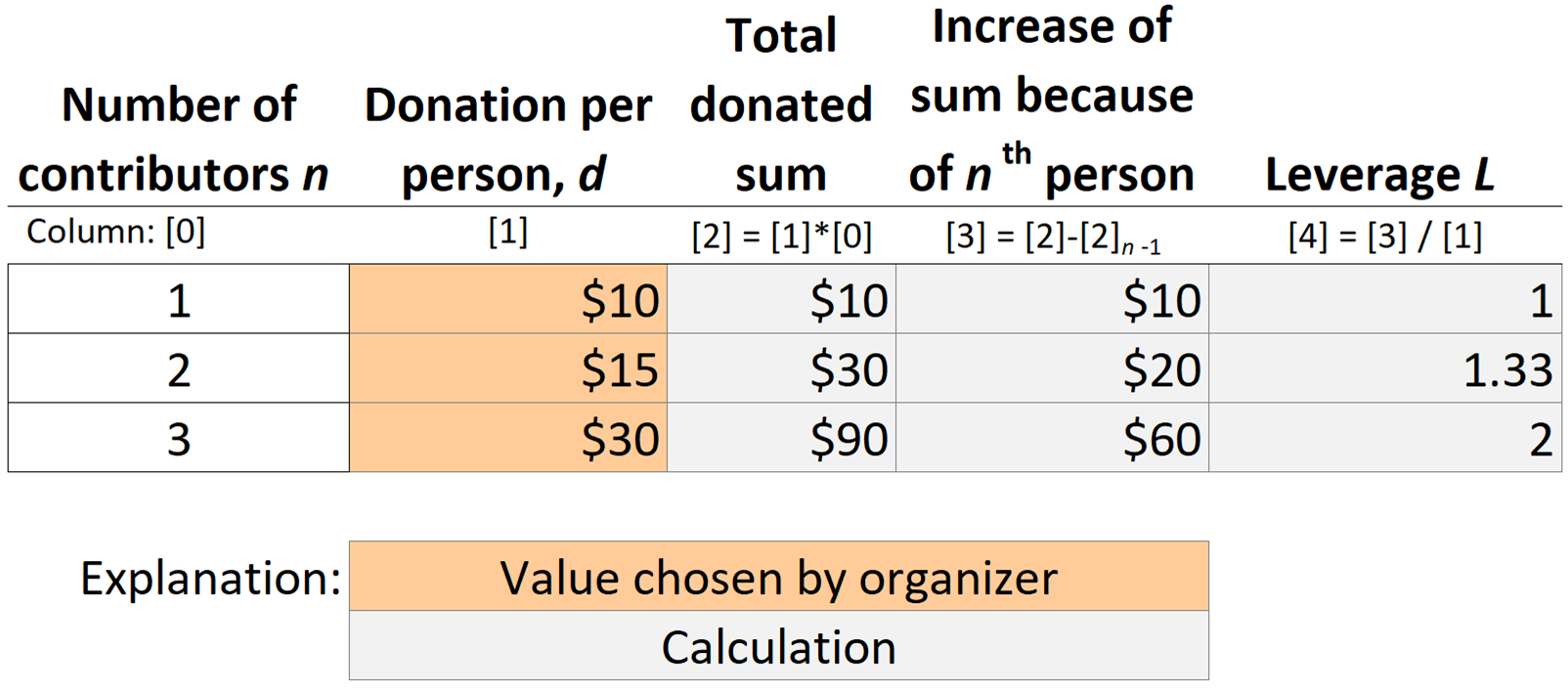
The contribution schedule, and the pool of potential contributors, have to be predefined by a central agent, the donation collector, whose decision on the progression of the donation schedule (column [1]) also affects how leverage (column [4]) increases with the number of contributors. It is easy to see that leverage always remains lower than the number of participants, L < n (for all n>1).

For this illustration, we directly expressed the donation schedule as a function of the number of participants. More to the point is to recast it as a function of the leverage factor: Donate $10 if leverage is 1, $15 if leverage is 1.33, etc. After all, the main effect we want to capture is the increased incentive to donate when more bang per buck is achieved (see the previous section).

The full-fledged version of Mutual Matching allows for arbitrarily many participants and individual scaling of donation schedules.

Transparency?

Suppose the donation collector publishes the collected sum. In that case, donors can readily verify that the promise of the leverage is fulfilled, by tracing the above calculations. In larger and more flexible versions, transparency may be increased by publishing information about the pool of candidate contributors (before commitments are collected) and about individual commitments received. Cryptographic tweaks or external auditing bodies could help improve transparency while protecting privacy.

Simplified Version with many participants

For simplicity, this section focuses on the case with large participation numbers. The solution becomes analytically more complex with few participants, although it remains numerically trivial (see the illustration for three persons above). The case of individually scaled contribution schedules is discussed in the yet-to-be-finalized paper. Further below, I consider some key takeaways from that extension.

The organizer, interested in collecting the largest sum of voluntary contributions, in the simplest version here, defines a consistent set of two curves:

• A leverage schedule, L(n), defining how leverage L increases as a function of the number of contributing voluntary donors n,
• A donation schedule, d(L), defining how individual donation levels increase as a function of leverage L.

She invites a fixed pool of candidate contributors to the scheme. Participants opting-in commit ex ante to donating d(L) for any possible leverage L the organizer can guarantee ex post. For example, with d(3) = $5 and d(4) = $14, opting in means you’ll contribute $5 if the organizer can show that without your participation, the sum of contributions would drop by L · d = 3 · $5 = $15, and you’ll instead contribute $4 if without you the sum dropped by 4 · $14 = $56. Hence, we say your contribution’s effect on the total collected equals your contribution amplified by the leverage L.

The organizer must ensure that her promise of each contributor’s leverage is fulfilled. It may not be intuitively obvious that this is possible given that she does, by design, not have any funds of her own at her disposal.^[3] What helps is that she can determine the equilibrium leverage ex post, after receiving the participants’ commitments. It turns out that for any leverage schedule L(n) (also written L_n) that grows slower than the number of participants, L_n < n (for n > 1), there exists, except for one degree of freedom in the form of a proportional scaling, exactly one general donation schedule d(L) for which the leverage-promise is met for each contributor, independently of their exact number. The degree of freedom as proportional scaling means, for a valid schedule d(L) identified, all multiples α · d(L), for positive α, are allowed too.

Although the organizer can therefore freely choose the progression of the leverage schedule, the leverage fulfillment requirement governs the progression of the donation schedule: The funds collected subject to any given person i participating must be L times his contribution d higher than the funds collected had he not participated, $n\cdot d\left(L_n\right)=(n-1)d(L_n-1)+L_{n}d\left(L_n\right)$. For any leverage schedule starting from a minimum of any n ≥ 1 contributors (for which it is debatable whether one would strictly want to impose $L_{\underset{–}{n}}=\underset{–}{n}$), and for a starting donation $d\left(L_{\underset{–}{n}}\right)=d_{\underset{–}{n}}$ that can be freely chosen, this leverage-fulfillment equation defines the exact shape of the required donation path,

For rapidly rising leverages L_n, this function exhibits a rapid exponential increase with the number of contributors. Note that in the limit case where $L_n\approx n\text{for}n>\underset{–}{n}$, the required donations would increase arbitrarily quickly (or large third-party funds would be necessary). But for leverage factors that increase slowly enough, the donation schedule can increase at a slower rate.

For arbitrary leverage schedules L_n, it can be difficult to interpret Eq. 1. In the following, we focus on the most straightforward example: a leverage schedule starting at $L_{\underset{–}{n}}=\underset{–}{n}=1$ and increasing linearly with the number of participants. One can show that in this case, for any slow enough increase of the leverage with the number of contributors,^[4] the donation schedule becomes

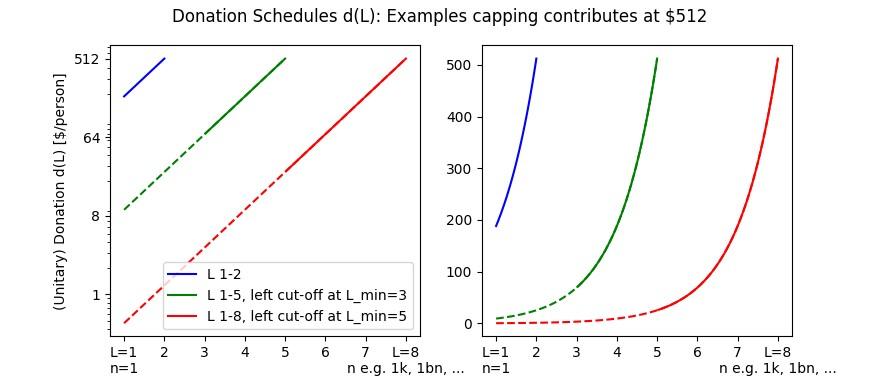
This exponential increase of the contribution with the equilibrium leverage L seems to be the most critical point for implementation of the scheme, limiting the realistically achievable leverage in a case with large uncertainty about the number of donors: The value of $d_{\underset{–}{n}}$ can be scaled appropriately to ensure a palatable donation for any specific leverage level, but if the absolute value of the leverage changes too rapidly as a function of the exact number of contributors, the equilibrium per-contributor donation $d\left(L_n\right)$ could quickly become underwhelming for the organizer if fewer than expected end up contributing, or overwhelming for the donors if more than expected contribute. This can always be avoided by a lower ambition for the leverage factor: A leverage factor L > 1 close enough to 1 can have an arbitrarily flat donation schedule, meaning the organizer can ensure that no one’s contribution drops or grows too much because of unexpectedly few or many contributors. In this case, of course, the gains from the scheme are limited too.

The organizer can limit the range of participant numbers (and thus of leverage factors) for which the scheme will be executed. In many instances, the upper cut-off point may be a compromise chosen so that it reassures donors that they won’t have to contribute too high sums, all while ensuring that (i) sufficient donations may be collected even if the number of participants is on the lower end of the expected range, and that (ii) there is only a low probability of an excessive participant number leading to the cancellation of the scheme.^[5] With a harmless sleight of hand, the organizer can, if she deems it helpful, define a lower bound (of participants and thus of leverage) below which no funds are collected. This could help to avoid a requirement for anyone to contribute if the leverage is too low for contributors to have any willingness to contribute.

Figure 1 illustrates some example donation schedules for this simplest case, including cut-off points beyond which the donation collection will not be executed.

Extension to Scaled Contributions

Mutual Matching can readily be extended to the case where the voluntary individual conditional contributions across persons are ${\alpha }_i\cdot d\left(L\right)$ instead of $d\left(L\right)$, with the individual scaling factors α_i > 0 either being set centrally by the organizer,^[6] or even freely pre-committed to by the individual donors. As long as each donor only has a small share of the total contributions (${\alpha }_i\ll {\sum }_j{\alpha }_j$), the analytical approximations that lead to the simple main results remain valid. The extension essentially leads to an equilibrium where an individual participant has the same impact that α_i independent donors without scaling of the based contribution schedule, d(L), would have (assuming integer α_i>1). The math, however, changes for small participant numbers, where ${\alpha }_i\ll {\sum }_j{\alpha }_j$  is violated; I have yet to determine to which degree the exact solution becomes more complex in this case.

If useful in order to contain the uncertainty about the total expectable contributions, the organizer can limit the allowed factors to any desirable (general or individualized) range when individuals themselves choose their scaling factors α_i.

Combination with Traditional Donation or Matching

• Nothing prevents the organizer from allowing donors to freely choose between donating a freely chosen (unconditional) amount and participation in the Mutual Matching co-incentivization scheme. In theory, especially with high enough leverage and thus convex enough donation schedules, there can be cases where it is preferable for some to contribute an unconditional, fixed amount, to prevent donating less than one would desire, or too much, depending on the exact amount of co-incentivization contributors. Hence, the additional ‘traditional’ scheme could be implemented as a no-regret fallback. The possible drawback of offering the traditional donation form as an additional ‘outside option’ for probable donors, is that it may make it more difficult to anticipate the amount of contributions in the co-incentive scheme, making calibration more difficult.
• Traditional matching based on a central donor matching fund can readily be combined with Mutual Matching—although this could increase complexity and, therefore, cognitive costs to participants. The central matching fund’s leverage (often based on a contribution 1:1, i.e. leverage factor 2) can then be multiplied with the base leverage L from the decentralized scheme proposed here.

Interpretation

It is beyond the scope of this post to enter into all analytical subtleties, extensions, advantages, caveats, and practical implementation details, of which many are relevant; a more exhaustive discussion paper is in progress. Some major points are as follows:

1. A generalizable decentralized donation co-incentivization without a centralized donation matching fund is possible. The requirement is that each voluntary donor pre-commits to contribute a (fixed or individually scalable) donation amount as a function of the verifiable equilibrium leverage factor that the organizer determines after receiving the donation commitments.
2. The limit to the achievable leverage stems from uncertainty around the total amount of commitments. On the one hand, we may expect many contributors’ willingness to donate to grow substantially as the leverage factor increases. On the other hand, the exponential increase of required per-person donations with the final leverage (and thus with the volume of committed conditional contributions) risks growing even more quickly, especially on the upper tail.
3. A small leverage L > 1 but close enough to 1 always seems achievable and may be preferable to fully independent, un-geared contributions. Although, for too low leverages, implementing the scheme may, of course, not be worthwhile in practice.
4. Especially in situations with reasonably predictable contributor numbers (or, in the extension with scaled contributions, with a predictable sum of contribution-scale-weighted contributors), Mutual Matching may allow collecting donations with leverage factors much above 1. I expect this situation to occur predominantly in reasonably homogeneous groups of participants, either willing to contribute with a predefined unitary donation schedule or with reasonably predictable individual scaling factors on a unitary donation schedule. Or, in repeated donation rounds with reasonably stable propensities to contribute (although repetition begs questions about theoretical strategic incentives of highly forward-looking contributors who consider the impact of their donation on the result not only of the current round but equally on the design of future rounds).
5. Theoretically, one can optimally calibrate the Mutual Donation scheme for a given distribution of stylized donor preferences (utility functions) and estimate the gains achievable compared to a traditional donation collection. Given the complexity of human behavior (particularly when it goes to a collaborative effort to altruistically support PGs), it might, however, be more insightful simply to try a scheme out in practice. An additional relevant dimension of the problem, not explicitly addressed in this post, is the relationship between the amount of donations received and the marginal impact of funding for the utility provided through the PG (related to the room for funding of the project).
6. Observations about the success of traditional donation matching and informal discussions about the scheme hint that a commitment to donations increasing as a function of the achieved leverage, as a principle, corresponds well to common donors’ preferences. However, theoretically, caution seems warranted. A stylized utilitarian (EA?) donor could exhibit a stepwise willingness to contribute: her preferred contribution towards the given cause remains strictly zero up to a certain leverage threshold, beyond which it jumps to a significant share of her disposable income, and there onwards gradually increases as a function of the leverage.^[7] In practice, this may not be a major challenge for the scheme. The application of the scheme is not mainly thought to be relevant for EAs as donors. Furthermore, even the stylized utilitarian could participate with a positive commitment to our scheme if the probability of high leverage factors is large enough, despite her (potential) underlying preference to contribute zero at a low leverage factor.^[8]
7. Is the cognitive and organizational cost for all involved in the scheme, including the requirements for trust, transparency, etc., warranted? If the core idea has enough appeal—surely only for a limited subset of PG problems in a subset of domains of life—it seems imaginable that our era, of apps and thousand social network types, is just the right time for the introduction of something in the direction of Mutual Matching.

I am keen to hear whether any funding seekers have a concrete interest in discussing a possible application of the scheme in situations where they think the key caveats might not entirely rule it out, and whether someone is aware of existing similar schemes – and, of course, any other comments.

^[1] See e.g. Jeff Kaufman’s post and GiveWell for critiques of donation matching. Moreover, here just as anywhere else where somebody is being incentivized to donate to a particular cause, there is a risk that the attracted donation would have otherwise been given to a similarly valuable cause (see e.g. Ben Hoffman’s post). For example, any fundraiser should strictly speaking take this into account, independently of whether he employs a leverage-based scheme or not. This risk could also be overstated. Most people are far from a stylized EA who’d live on a fixed budget and donate the rest. Instead, I expect many people donate more unsystematically where they more or less spontaneously seem fit, without an individual donation reducing other personal ones elsewhere so clearly (I have not looked for empirical evidence on this question).

^[2] I believe this can be a strong drawback in the literature. I may not be willing to contribute more mainly because a lot is being given (all else equal, I might in some cases even want to give less if more is already given by others), and I may not be very keen to match others’ donations if I don't know their counterfactual contributions. Rather, I may be mostly willing to give if I know my contribution increases others’ donations by a specific amount.

^[3] The scheme can readily be extended to the case where she commands additional funds.

^[4] If instead leverage increases more rapidly with the contributor number, the result qualitatively still looks rather similar.

^[5] Merely keeping the leverage constant above a certain threshold would lower the rate of increase of the donations with the number of contributors, but would not allow these donations to remain constant.

^[6] Maybe based on presumed preferences for the good in question and/or set proportional to GDP (if donors are countries) or personal income (for individual persons).

^[7] Theoretical outcome in presence of competing causes, each with large room for funding relative to the utilitarian’s wealth. In contrast, in 2018, median (annual) donations among different EA categories were $640-$1000, see EA Survey 2019.

^[8] Of course, none of these points prove that the particular shapes of the donation schedules that are feasible are highly attractive to donors and conducive to high eventual equilibrium donations.