Tax Cuts and Innovation

The classic turn in metascience goes like this: Policy discussions about R&D usually focus on how much we should spend: should we double the NIH budget or should we stop subsidizing university nonsense? The meta-scientist notices that some types of science funding are tens if not hundreds of times more effective than others. If we can shift spending into more efficient mechanisms we could 10x R&D output without spending a dime. Instead of focusing on how much money we should spend on science, we should focus on how to spend money on science.

But what if the most important metascience policy wasn’t about spending at all?

Taxation and Innovation in the 20th Century is a 2018 paper by Ufuk Akcigit, John Grigsby, Tom Nicholas, and Stefanie Stantcheva that provides some answers. They collect and clean new datasets on patenting, corporate and individual incomes, and state-level tax rates that extend back to the early 20th century. The headline result: taxes are a huge drag on innovation. A one percent increase in the marginal tax rate for 90th percentile income earners decreases the number of patents and inventors by 2%. The corporate tax rate is even more important, with a one percent increase causing 2.8% fewer patents and 2.3% fewer inventors.

Methods

Before considering what these effects mean for metascience policy, let’s make sure we can believe them.

The authors have a table of data where each row lists the state, the year, and the number of patents, the tax rates, and lots of other variables in that state-year.

The authors analyze this data with three different methods:

The first method is the simplest. They just regress the patent output of a state on it’s tax rate 3 years prior, with state and year fixed effects and some other basic controls. Fixed effects are flexible ways to control for differences across states or across time that would bias the regression and mask the causal effect of increasing taxes on patenting.

For example, California has high levels of innovation and high taxes. A simple regression would use this data point to support a positive relationship between innovation and taxes. But is this relationship really because high taxes cause more innovation? Or is it some characteristic of California that both draws innovation and allows for high taxes like the nice weather, for example.

Including a “California fixed effect” makes the regression only look at the times when California’s tax rate increased above or below it’s all-time average. If higher-than-average tax periods are followed by periods of low innovation, that’s evidence that high taxes decrease innovation even though all the California-year observations are both high-tax and high-innovation.

Similarly, the mid-20th century had low taxes and lots of innovation, so a basic regression would count that as evidence that high taxes decrease innovation. But including year fixed effects compares each state’s tax rate to the national average that year. So even though all observations from 1950 are low-tax and high-innovation it might be that the states with the highest innovation in 1950 also had the highest taxes relative to their peers.

This “OLS plus fixed effects” method filters out false causality that arises from fixed state differences or national level trends, but it still fails if California’s tax rate deviates from it’s all-time average and the national average in response to a change in innovation/patenting. So there are still reverse causality concerns.

The second method uses changes in the federal tax rate as an instrumental variable to predict the total tax burden faced by a firm or inventor. If we just looked at how innovation changes after a state raises taxes, we could get a biased estimate because of the reverse causality we mentioned above. States probably raise taxes in response to an innovation boom in their borders. So if we split up state-year observations into two groups, high tax burden and low tax burden, and then compared the innovation in each group we might see a positive relationship because all the high innovation states raised taxes in response to booms.

However, if we instead split up our observations based on changes in the federal tax rate, we would avoid a lot of this reverse causality. Changes in the federal tax rate are good predictors of the total tax burden on inventors but they aren’t as influenced by individual state-level booms. So the high-tax burden group as predicted by the federal rate still has a much higher tax burden on average but they aren’t much more likely to be living in an innovation boom state.

This method can avoid many of the problems of the OLS model because state-level reverse causality won’t bias this variable. National tax rates could still respond to changes in innovation and bias this estimate though.

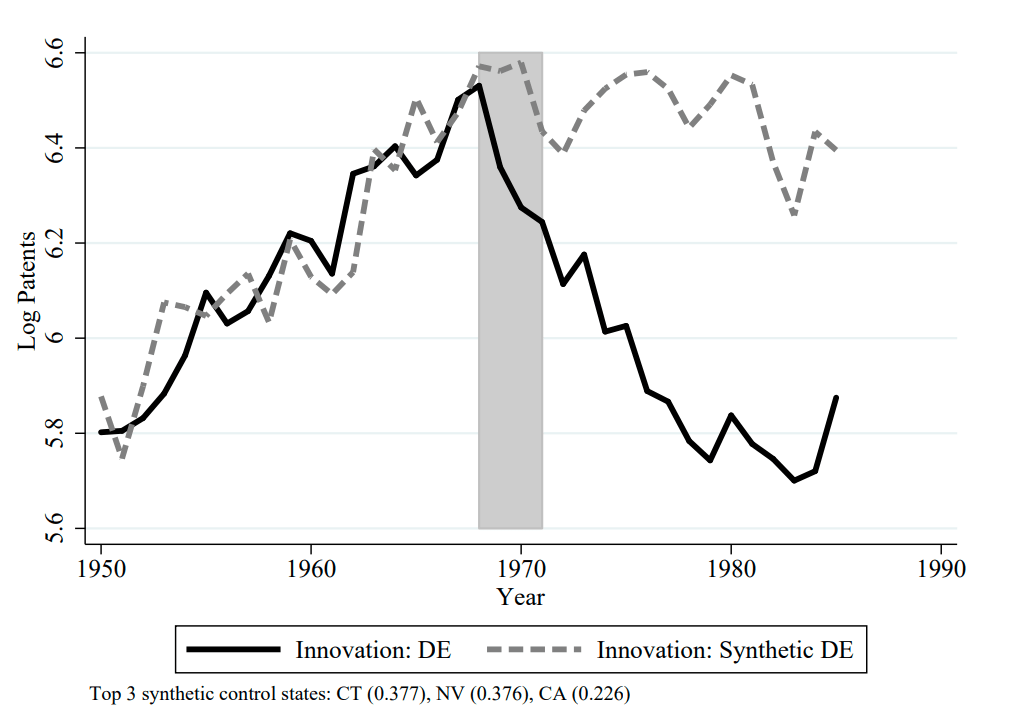
The final method sets up some quasi-experiments where two states, or a state and a weighted average of other states, have coincident innovation trends up until one state has a big change in tax rates and then tracks how those innovation trends diverge.

This method relies on the assumption that if two state’s innovation trends match for several years, that we they will continue to match unless one state changes something that the other does not. There are lots of ways to make this more or less believable but pre-treatment match can always be coincidence and post-treatment divergence may have multiple sources.

All of these methods have potential problems, but all of the problems are different. The authors find just about the same results with each method: a one percent increase in the income tax decreases patenting by 1.5 - 2.5%. It’s easy to believe any one of these methods is mistaken but it’s difficult to imagine a data generating process which makes all of these perspectives wrong and wrong in exactly the same magnitude.

An important clarification on interpreting these results is that because they are state level, they are tracking the effect of state tax rates on inventor output and on the location of that output. If we only care about national level output we might not mind if state tax rates just move inventors around the country.

The authors are aware of this and try to isolate the output effects from the migration effects. State tax rates affect output because migration is not costless and because there are agglomerations of inventor communities, like in Silicon Valley, that become much less productive if they are dispersed across the country (or if fewer people migrate towards them than they would have otherwise).

Using both a model of location choice and an empirical specification looking at federal tax rates, they find that the larger effects of the corporate tax rate are mostly due to to migration, the effects of the individual tax rate are mostly due to output changes. Patenting corporations are usually large, so it’s easy for them to move R&D expenditures across states. The direction of the effect is still the same, corporate taxes probably reduce patenting by firms, but the magnitude is about half as large and it’s not as confidently estimated. But the individual income tax effects are basically just as large and significant. A one percent increase in the individual income tax decreases the number of patents and inventors permanently by 1.7-1.9%. These patents are destroyed, not just sent to neighboring states.

Metascience Tax Policy

When I first read this paper I got the sense that these effect sizes are really big. The economists I asked about it agreed. Partly, this is based off of a comparison to other findings. Arnaud Dyèvre, for example, finds that a 1% increase in agency funding (e.g to the NIH) increases the patents assigned to that agency by .4%.

But when you think about it, findings like these are really difficult to compare. They both find effects on patenting, but the both the input and output are in percentage terms with completely different bases. Dyevre says a 1% increase in NIH funding (~$500 million) leads them to .4% more patents (how many patents is that?). Akcigit’s baseline regression says a one percent decrease in the marginal tax rate for 90th percentile earners (what’s the dollar value of this?) increases state-level patents by 2%.

So is lowering taxes a cheaper way to induce innovation than spending money on R&D or not?

Here's my current back of the envelope calculation of this:

Federal income taxes paid by the top 10% of earners is 1.6 trillion. So decreasing the marginal tax rate for those earners by 1% costs 16 billion. According to Akcigit’s federal level regression, this is supposed to increase patenting by 1.9%. 1.9% of ~350,000 patents a year is 6,650 patents. So 6,650 patents for $16 billion or about $2.5 million per patent. This seems pretty reasonable. One point of comparison I found is this Pierre Azoulay paper which claims "An additional $10 million in NIH funding generates 3.1 additional private-sector patents" which is a very similar, but slightly higher, price per patent.

So reducing taxes isn’t a much cheaper way of inducing patents, but cutting taxes has big effects on growth rates through channels other than innovation. Plus, we might think that privately allocated research effort is better matched to social value than whatever university scientists can get through the NIH committee.

Reducing income taxes is an underrated lever for increasing growth rates and accelerating technological progress. All economists agree that firms and inventors are not sufficiently rewarded for the contributions their ideas make to social welfare. Usually they plan to rectify this using some form of subsidy: grants, prizes, advanced market commitments, or patent buyouts. But the first thing we should do is stop taxing the fraction of the surplus they do capture!

Reducing taxes and spending on R&D need not trade off with each other. It would be a tragedy if we funded tax cuts with cuts to spending on the world’s most important positive externality. But tax cuts should be a bigger part of any conversation about using policy to improve economic growth and technological progress. They are simple, efficient, and they don’t share the risks of active forms of subsidy that can be ineffective or even counterproductive when designed poorly.

Reducing taxes is a first-order point of leverage on innovation and economic growth.