[Edit: 11/02/2021: changed how results were calculated in response to Aidan's comments.] [Edit: 03/09/2020: a few minor typos corrected.]
Summary[1]
To determine how to do good as cost-effectively as possible, it is necessary to estimate the value of bringing about different outcomes. We briefly outline the recent methods GiveWell has used to do this. We then introduce an alternative method – Well-Being Adjusted Life-Years, or ‘WELLBYs’ – and use it to estimate the values of two key inputs in GiveWell’s analysis: doubling consumption for one person for one year and averting the death of a child under 5 years old. On the WELLBY approach, outcomes are assessed in terms of their impact on subjective well-being – here, we use self-reported life satisfaction.
Our primary aim is to show that the WELLBY approach could be used, rather than that it should be used. Our estimate of the relative value of the two outcomes should be taken as preliminary rather than definitive.
We estimate the effects of doubling consumption using evidence from randomised controlled trials of cash transfers in Kenya conducted in collaboration with GiveDirectly. The total effect of the transfers is calculated by inferring an annual decay in life satisfaction. We include intra-household spillovers but exclude, due to mixed evidence, inter-household effects[2]. To account for uncertainty in our model, we input 90% subjective confidence intervals and run Monte Carlo simulations.
The value of saving a life to the person whose life is saved is estimated on two philosophical views of death: deprivationism (the disvalue is the total lost life satisfaction) and the time relative interest account (TRIA) (the disvalue is total lost life satisfaction, discounted by the psychological connectedness to one’s future self). In effect, deprivationism holds it’s better to save 2-year-olds than 20-year-olds; TRIA the reverse. We also assess the effect of grief on family members using life satisfaction data.
These estimates rely on certain (implicit) philosophical assumptions. We note how different assumptions would substantially change the results and reduce the relative value of saving lives. These issues are separate from how or whether to use WELLBYs; given different assumptions, one would simply calculate the WELLBYs differently. Our task is only to highlight the implications of (some) theories, rather than evaluate them.
Our model estimates that the value ratio of averting the death of an under-5 to doubling consumption of one person for one year is 154:1 on deprivationism and 33:1 on TRIA. For reference, GiveWell currently uses a ratio of 100:1[3], based on a staff aggregate of 47:1 and an estimate of 230:1 from IDinsight’s beneficiary preference survey (described in the main text).[4]
We close by setting out various uncertainties with the WELLBY estimate that are tractable with further research: the effects of cash transfers over time; spillover effects (of cash transfers and of deaths); the location of the ‘neutral point’ equivalent to non-existence; and the impacts assessed in terms of happiness rather than life satisfaction.
Introduction
There are many ways to help others. Anyone allocating resources towards this end – ranging from policy-makers disbursing government budgets to individuals giving to charity – must choose between programmes with different outcomes, such as averting deaths, alleviating poverty, enhancing education and improving mental health. Comparing the value of these outcomes is a difficult, but necessary, task if we want to use these resources to benefit others as much as possible.
Much of the research to identify the world’s most cost-effective charities is produced by GiveWell. GiveWell is currently re-considering their framework for assessing the value of outcomes, what they call ‘moral weights’. Therefore, we (at the Happier Lives Institute) thought it would be timely to present one method for comparing the value of different outcomes: using well-being adjusted life years, or WELLBYs. On the WELLBY approach, measures of subjective well-being (SWB), self-reports of happiness and life satisfaction, are used as the common currency by which the impact of changes is measured. We use this approach to estimate the (relative) values of two of the three key outcomes in GiveWell’s model: doubling consumption for a year and averting the death of a child under 5 years old. While this post is focused on GiveWell’s framework, this method is generally applicable.
We first set out GiveWell’s approaches to date. Then we introduce our alternative, make an initial estimate using it, and compare the results.
Our main purpose here is not to argue that the WELLBY method should be used, although we will briefly motivate it later. Rather, we want to show how it can be used; this post is intended as a ‘proof of concept’. We aim to introduce readers to the methodology and to provide an initial review of the SWB data available in the contexts we are interested in – very low-income populations. We consider our estimate preliminary rather than definitive; we caution against strongly updating based upon it. We mention later the further empirical and theoretical work that is required.
GiveWell’s approaches to date
GiveWell’s cost-effectiveness model uses three main outcomes:
- Doubling a person’s consumption for one year.
- Averting the death of an under-5-year-old.
- Averting the death of an over-5-year-old.
In the past, GiveWell determined its moral weights by first asking its staff to give their own estimates of the relative value of the three outcomes. The median of the staff’s assignments was then used as the relative values of these outcomes in their cost-effectiveness analysis. This method allows disagreements to be resolved – it appeals to a sort of wisdom of the crowds – but it does not answer the question of how someone might, in the first place, form a justifiable, evidence-based view of what the appropriate moral weights are; staff members were free to choose their own method. What method might someone use?
An option, and one GiveWell has recently explored, is ‘beneficiary preferences’. IDinsight, a research organisation, conducted surveys in Ghana and Kenya to capture the choices of the beneficiaries of the programmes that GiveWell recommends (full report). IDinsight asked individuals both for their ‘willingness to pay’ to reduce the risk of death to themselves and their children, and to choose – taking the perspective of a decision-maker in their community – between programmes that save a life or provide a number of cash transfers. We briefly discuss the specific methodology and the result of these surveys later.
While reliance on preferences (revealed or stated) to determine the value of outcomes is standard in economics, the approach faces an array of challenges – see Bronsteen, Buccasfuso and Masur (2013) for an extensive review. One unavoidable difficulty of using preferences is that they rely on people making predictions about how various hypothetical situations would affect themselves (and others) if they happened. Psychological research into affective forecasting has demonstrated that people are not very good at predicting how they will feel and such forecasts suffer from a number of biases (Gilbert and Wilson 2006). One example is focusing illusions, where we overrate the effect of easily imaginable factors (Kahneman et al. 2006). Even for revealed preferences (choices people actually make, and often seen as the gold standard by economists) people still need to forecast how they will feel as a result of their choice. Kahneman and Thaler (2006) argue decision utility (what people choose) and experienced utility (how they feel) are therefore practically different. As it is much easier for individuals to say how they currently feel, this is a central advantage of using reports of subjective well-being to value outcomes, assuming experienced utility is valuable.
The well-being adjusted life year (WELLBY) approach
WELLBYs, in structure, are quite similar to the well-established quality and disability adjusted life year (QALYs and DALYs) health metrics, which combine quality and quantity of health into a single number. A year in perfect health is worth 1 QALY, whereas a living for a year with a condition that had a utility weight of 0.5 would be worth 0.5 QALYs, and so on[5]. A QALY weight of 0 is equivalent to being dead, and there can be states worse than death (Tilling et al. 2010). Every Q/DALY is taken to have the same benefit to one person as another, which then allows health treatments to be compared for cost-effectiveness (if cost information is known). Q/DALY weights for different health states are determined by asking people to make hypothetical trade-offs between health states, and hence use the same underlying method as the beneficiary preference approach.
The key difference is that WELLBYs are constructed by using measures of subjective well-being, namely self-reports of happiness and life satisfaction (Frijters et al. 2020; Birkjaer, Kaats and Rubio 2020). One WELLBY, in this document, is equivalent to a 1-point increase on an 0-10 life satisfaction scale for one person for one year. Life satisfaction is typically measured by asking “Overall, how satisfied are you with your life nowadays” (0 - not at all, 10 - completely). A difference is that a QALY weight of 0 is equivalent to being dead, while life satisfaction scales do not have a clear ‘neutral point’ equivalent to non-existence, an issue we return to later.
While researchers have surveyed SWB for several decades (Diener, Lucas and Oishi 2018), proposals to base decision-making on SWB are relatively recent, and have mostly been focused on public policy-making in high-income countries (e.g. GHC 2018; O’Donnell et al. 2020). Efforts to use SWB to assess cost-effectiveness in low-income contexts are even more nascent.[6]
We break our WELLBY estimate into several parts. We first discuss the effect from doubling consumption, then averting the death of a child under 5. In both cases, we start by considering the ‘direct’ effects: those on the person whose consumption has doubled, or who has died, respectively. We go on to consider the effects on the household of that person, in each case. We briefly discuss effects on the wider community but do not include these in our model, as they would be very speculative.
A model of this analysis in Guesstimate can be viewed here.[7]
Guesstimate allows users to input their uncertainty (and its distribution) for each parameter. Guesstimate runs Monte Carlo simulations, which are reruns of the same calculation using random values from the probability distribution for each parameter. This means that you can produce an estimate of the uncertainty for the value of the outcome . We describe the inputs to our model throughout the post.
A final comment before we begin: the choice to base WELLBYs on life satisfaction, rather than happiness, may seem controversial to some. There is a long-standing view that well-being – what ultimately makes our lives go well – consists in happiness (a positive balance of pleasant over unpleasant conscious states) as opposed to anything else, such as life satisfaction (a judgement of how life is going overall). While we have sympathy with this view, we are pushed to use life satisfaction data because they are so much more abundant than happiness data. When more data are available, it would be straightforward to replace the inputs in our model. It remains open exactly how much difference this would make to prioritisation decisions in practice: research indicates that what makes people happier tends to also make them more satisfied with their lives, although some things have a greater impact on happiness than life satisfaction, or vice versa (Kahneman and Deaton 2010; Boarini et al. 2012).[8] In any case, the use of either subjective measure enhances our understanding of what impacts people’s lives.
Estimating the effect on SWB from doubling consumption for one person for one year. [9]
Estimates from existing literature
We start by presenting effect sizes of SWB in standard deviations, (as is standard in the literature.[10] Previous cross-sectional[11] work looking at the relationship between income and life satisfaction (LS) in low-income countries suggests that doubling income leads to an increase of 0.24[12] standard deviations (SDs) of life satisfaction.[13]
Historically, much of the causal literature on the effect of income on SWB came from lottery studies. A notable recent study in this vein by Lindqvist et al. (2020) estimates that among Swedish lottery winners (surveyed 5–22 years after the lottery), a win equivalent to doubling annual income for 20 years causes an increase in life satisfaction of 0.26 SDs[14]. The standard deviation of LS is 1.93 in this study (see Table 3), so this roughly equates to a change of 0.5 LS points.
Direct effect of doubling consumption on recipient
Recently, studying the effects of providing cash transfers (CTs) in low-income countries via randomised controlled trials (RCTs) has provided further and more relevant causal evidence. Results from several studies done in collaboration with GiveDirectly are presented in Table 1. We base our Guesstimate model on these studies. Egger et al. (2019) has the largest sample size, and is the most similar to GiveDirectly’s current programme. In a forthcoming meta-analysis McGuire, Bach-Mortensen and Kaiser (n.d.) will consider a much larger number of studies[15], and will present a more formal approach to aggregation.
Table 1: GiveDirectly studies. PPP = Purchasing power parity; SE = standard error; SD = standard deviation.
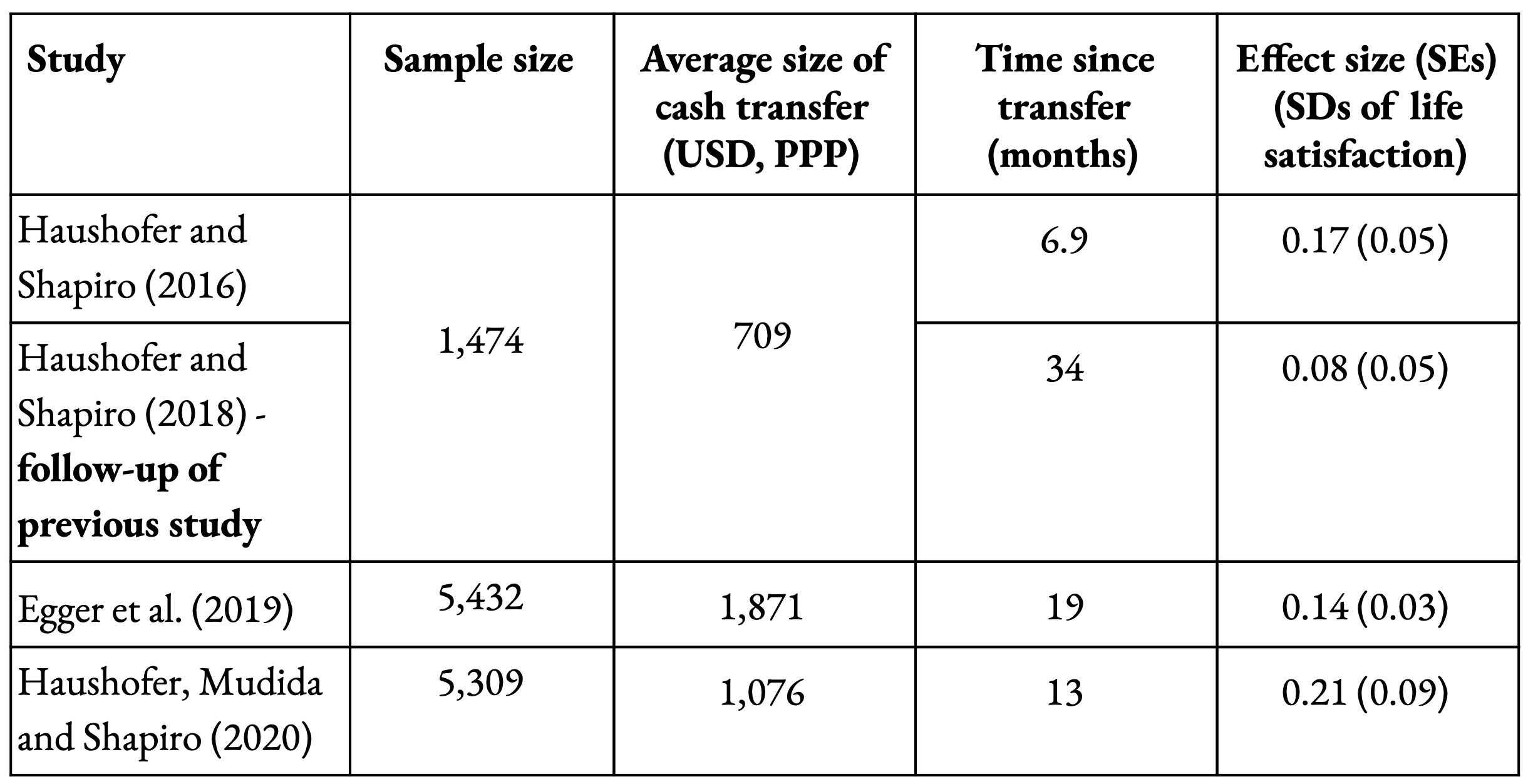
Table 1: GiveDirectly studies. PPP = Purchasing power parity; SE = standard error; SD = standard deviation.
As you can see in Table 1, the size of the CTs range between $709 and $1,871, and the average time the surveys are conducted after receiving the CT ranges between 7 and 34 months. Given that both of these factors likely affect the measured effect size, combining the results in Table 1 is not trivial. We next describe our model based on this information; we hope to improve on the aggregation in our future work by incorporating more studies.
We construct a simple exponential decay model for the SWB effect through time, by saying that the effect will be some fixed percentage compared to the previous year:
SWB (1)
where SWB is the effect size (in SDs), c is a constant (the effect at time = 0), d is the annual decay rate of the effect size, and t is the time in years. We estimate the parameters that best fit this equation based on the four data points from the GiveDirectly studies.[16] Figure 1A shows the central estimate, as well as the 66% and 90% confidence intervals. The central estimate corresponds to an annual decay rate of 32% and an initial effect size of 0.26 SDs. We input the confidence intervals inferred for these parameters into Guesstimate. Figure 1B shows the distribution of 5000 samples of each parameter, and Figure 1C shows the resulting trajectories (i.e. a reflection of the Monte Carlo simulations run in Guesstimate).

Figure 1: Exponential decay model of life satisfaction effect size (in standard deviations) through time. (A) Measured LS effect sizes from the GiveDirectly studies are shown as coloured circles. The central estimate, 66% and 90% confidence intervals of the model, fit with a linear regression, are shown. (B) 5,000 samples of the distributions of decay rate and initial effect size shown as histograms. (C) The trajectories of LS through time based on the samples of parameters shown in (B). This illustrates the Monte Carlo simulations run in Guesstimate.
Modelling the effect on SWB through time based on only four data points is unfortunate, but the most justifiable approach given the limited relevant information. The confidence intervals are correspondingly wide: 2–53% for the decay rate, and 0.14 to 0.48 SDs for the initial effect. A 32% annual decay rate implies the effect size falls below 0.05 SDs at five years and below 0.01 SDs at nine years. In Appendix 1 we describe other papers that study the effects on SWB through time, although each is dissimilar to the GiveDirectly studies in at least one way, and results are mixed, so we do not update our model in either direction. We do not let the effect continue indefinitely, but instead input a time of five years when the effect ends (90% CI: 2–10 years). The total effect through time in WELLBYs is the area under the curve (determined by integrating equation 1).
What’s the effect in WELLBYs?
To convert the effect size from SDs to WELLBYs we need to know the standard deviation (SD) of the life satisfaction (LS) data in the GiveDirectly studies. The baseline SD of LS for the shared sample used in Haushofer and Shapiro (2016, 2018) and reported in Haushofer, Reisinger and Shapiro (2019) is 2.66.[17] Other studies have a lower SD[18]; we put 1.9 to 2.7 as our subjective 90% confidence interval. We estimate the total effect on the direct recipient of a CT to be ~1.8 (0.6–5.0) WELLBYs.
Further considerations
We have not considered that raising income appears linked to life expectancy[19] and that higher reports of SWB[20] appear related to reductions in all-cause mortality.
Spillover effects
If we can, we also want to count the ‘spillover’ effects, the impact of an intervention on those besides the direct beneficiary (in this case, the recipient of the cash transfer). Here, we consider, in turn, spillovers within the household, i.e. to family members, and to those outside it, e.g. neighbours.
Haushofer and Shapiro (2016) administered surveys to the heads of the household receiving a CT; sometimes this was two people (usually a wife and husband), and sometimes this was one person.[21] Life satisfaction results are therefore already averaged across the heads of a household; we use the effect on the recipient (already estimated) as the average effect on the heads of a household. In the treatment group, there were 369 double-headed households and 102 single-headed households, which corresponds to an average of 1.78 heads per household.
We then need to estimate the spillover effects on other members of the household. There are no estimates of the direct impact of a cash transfer on the subjective well-being of household members who are not the household heads; this is a promising area for future research. However, positive spillovers seem likely for several reasons stemming from shared expansion of resources. Haushofer and Shapiro (2013) report large increases in household common goods such as livestock and furniture, and the likelihood of having an iron roof; households also spend about $25 more per month on food (see a summary from GiveWell here). In Egger et. al (2019), children's education and food security index improve. CTs appear to decrease children’s economic activity (de Hoop and Rosati, 2014), which is likely beneficial for mental health of children and adolescents (Sturrock and Hodes, 2016). CTs have been linked to a decline in the intergenerational transmission of depression (Eyal and Burns, 2019).
In the absence of much more information, we assume that the spillover effect on the other members of the household – aside from the household head(s) – has 90% confidence intervals of 20–100% of the effect on LS for the recipient. We note this is a non-trivial uncertainty given there are nearly twice as many ‘other’ members as heads of household.[22] Household size is reported in Egger et al. (2019) as 4.3, and in Haushofer, Reisinger and Shapiro (2015)[23] as 5.1; we input this range into Guesstimate. Our model calculates the total effect per GiveDirectly CT is 3.2 (1.0–8.9) WELLBYs to the head(s) of the household and 2.2 WELLBYs (0.5–6.9) to the other members of the household.
We do not include effects to those outside the household, because we are sufficiently uncertain of what they are – in this case but even more in the next section (averting a death). The most relevant, causal evidence of spillovers to the community is from the GiveDirectly studies themselves. Whilst Haushofer and Shapiro (2018) found evidence of negative psychological spillovers to the community, the more recent GiveDirectly studies (Egger et al., 2019; Haushofer, Mudida and Shapiro, 2020) – with larger sample sizes, and based on a version of the programme more similar to current practice – did not. A synthesis of studies that measured community effects suggests the spillovers to SWB are overall insignificant (see Appendix 2).
It’s worth noting the lack of negative community spillovers is unusual, in light of the wider SWB literature, although not necessarily surprising. In a review that draws on high-income country data, Clark (2016) argues there is a “considerable variety of evidence that well-being is relative in income”; in other words, it matters not just how wealthy you are, but how wealthy are those you compare yourself to, and hence others becoming richer would make you feel worse. The relative effect of income has been proposed as an explanation for the ‘Easterlin Paradox’, the finding that rising incomes do not seem to increase average happiness over the long run, even though richer people and countries are happier than poorer people and countries (Easterlin 2016; Kaiser and Vendrik, 2018). Clark notes that while the evidence indicates there is, in general, a relative income effect, it's unclear how large it is and whether it functions differently for those in poverty, a topic which has not received much study.[24] We welcome further research investigating relative income effects at these low levels.
Adjustment for doubling consumption
So far, we have considered the effects of receiving a CT on a household. However, GiveWell’s moral weight specifically concerns doubling consumption for one person for one year; we take two steps to reach an estimate for this value. Annual household consumption (rather than individual consumption) is reported in the GiveDirectly studies. The size of the CT is not the same as annual household consumption; our first step is to adjust the effect from the CT to reflect what proportion it is of doubling annual household consumption. Egger et al. (2019) state that the CT ($1,871 PPP) corresponds to 75% of mean annual household expenditure in recipient households. There is a roughly linear-logarithmic relationship[25] between income and LS (Jebb et al. 2018) (which means that income changes have less of an effect on LS at higher incomes). We use this relationship to adjust to a 100 % change in consumption (i.e. doubling) for one year, which increases the effect size by 24 %.[26] This is a non-trivial adjustment, and it is possible that a linear-log relationship does not hold in this context; this could be determined with further research. Secondly, we account for doubling consumption for one person (rather than the household) for one year. We do this by dividing the (modelled) effect of doubling household consumption by the average number of household members.[27]
WELLBYs Lost from Death of an Under-5
Direct Loss of WELLBYs from Death
Deprivationist account
We first estimate the number of WELLBYs lost due to the death of an under-5 by using the most mathematically simple approach: the badness of death is the total well-being the person is deprived of by not living longer, i.e. years of life lost multiplied by the counterfactual well-being. This is called the ‘deprivationist’ account of the badness of death.[28]
Life expectancy
We use Kenyan data, in line with the estimate from doubling consumption. The UN provides life expectancy estimates projected into the future[29]; for a one-year-old in Kenya, born in 2020-2025, the median life expectancy is 69.6 (95% CI: 68.9–71.5). GiveWell’s charities deliberately focus on helping the poorest, who are likely to have a lower life expectancy. Achoki et al. (2020) show the variation in life expectancy across Kenyan counties: in 2016, three counties had a life expectancy higher than 71 years, and 2 counties were lower than 60 years. In Guesstimate we input a 90% subjective confidence interval of 62–72 for life expectancy. We also input a uniform distribution of ages between 0 and 5 to represent children under the age of 5 years old.
Life satisfaction
Estimated average life satisfaction in Kenya is 4.4/10.[30] Again, this is probably not representative of beneficiaries of GiveWell-recommended programmes. For the GiveDirectly samples that report unstandardized LS scores, the baseline LS is 3.9 / 10 with a SD of 2.66 (Haushofer & Shapiro 2019). IDinsight asked an SWB question in their beneficiary preferences survey; those surveyed in Kenya had an average life satisfaction score of 2.3/10 (n = 1,808, SD = 2.32 ).[31] As IDinsight comments, this is lower than expected based on extrapolation of results from nationally representative surveys.[32] IDinsight suggests this could be because the life satisfaction question was asked at the end of their survey, biasing the answers, or because the rough linear-logarithmic relationship between income and LS does not hold at the bottom of the worldwide income distribution. In our model, we input a 90% subjective confidence interval of 2.3–4.4.
Accounting for the future
So far, we have focused on the evidence of the current SWB level. However, it is likely that average SWB will change in the future (as two examples, economic development may bring about positive effects on LS, but climate change could have negative effects). Forecasting future SWB is a promising area for future work, but so far, we have spent very little time on this. Nevertheless, it is clear changes to quality of life in the future could be large, so we want to account for this in the model.
On top of changes to quality of life, there are also risks from global, regional or national catastrophic events, i.e. risks (not incorporated in life expectancy) that could curtail their quantity of life and so total lifetime SWB.[33]
These two factors (change in levels of LS, and accounting[34] for future risks) are tricky to incorporate neatly in Guesstimate. Given this, and the fact that our current thoughts are somewhat speculative, we use one cell to combine these effects and make an overall adjustment. We estimate the subjective confidence interval for this adjustment in this spreadsheet, by considering upper and lower estimates of the final impact in WELLBYs. For the upper bound, we use an annual discount rate of 0.18%[35] and assume LS will rise linearly by 4 points over the next 70 years. For the lower bound, we use an annual discount rate of 0.4%[36] and assume that LS will stay the same. Compared to ignoring both factors, the upper bound estimate increases the WELLBY value caused directly by saving the child by 63%, and the lower bound reduces it by 17%. Hence, accounting for these, in our model increases the direct value of averting deaths.
The neutral point
An important and difficult question is where on the 0-10 scale is equivalent in value to non-existence; in other words, the level at which continued existence would be overall neither good nor bad for the person if they continued to live at that level. We refer to this as the ‘neutral point’.
It is not clear where the neutral point is and there has been little discussion of how, in principle, to determine this. SWB researchers sometimes treat the mid-point of SWB scales (e.g 5/10) as where someone is neither satisfied nor dissatisfied, or neither happy nor unhappy (e.g. Diener et al. 2018). If we took this as the neutral point, this would have the controversial implication that many people, including the average Kenyan, have lives currently not worth living (considering just their well-being). Other researchers treat the bottom of the scale, e.g. 0/10 for life satisfaction, as the neutral point (e.g. Layard et al. 2020). This has a different controversial implication: it is not possible for anyone, using a life satisfaction scale, to have a life not worth living.
One, not obviously correct, method would be to ask members of the public at what level they would be indifferent between existence and non-existence. A small (n<100) survey in the UK found that at a life satisfaction level of about 2/10 respondents would choose death over life[37]. The IDinsight beneficiary survey, using an equally small sample size, estimated the neutral point as being 0.56.[38] We use a range of 0.05–2.5 for the neutral point.
Summary: deprivationist estimate
The direct effect estimated by the deprivationist account is then:
(Deprivationist:) WELLBYs lost = (expected well-being level - neutral point) * (life expectancy - age at death) = expected net well-being * expected years of life
In words, the net WELLBY per year of life is the difference between the expected life satisfaction and the neutral point. The number of WELLBYs lost by a death is the net WELLBYs per year of life multiplied by the expected remaining number of years of life if the individual had lived. For example, if a child would have died at the age of four, the expected well-being level over their life-time is 4/10, and their life expectancy is 66 years:
(Deprivationist:) WELLBYs = (4 - 2) * (66 - 4) = 2 * 62 = 124
In Guesstimate, this works out to be about ~210 (50–360) WELLBYs lost due to the death of an under-5.
Time Relative Interest Account (TRIA)
On the previous estimate, it is more valuable to save the life of a 2-year-old than a 20-year-old. Some people find this unintuitive and think the reverse is true. In contrast to the 20-year-old, the 2-year-old is not yet fully developed, they do not have a strong psychological connection to their future selves, nor do they have as many interests that will be frustrated if they do not keep living.
In the philosophical literature, the view that captures the intuition that it is (usually) worse for someone to die at 20 than at 2 is called the time-relative interest account (TRIA) of the badness of death (Holtug 2011; McMahan 2019). On TRIA, the badness of death is a product of the future well-being the person is deprived of multiplied by how psychologically connected the person presently is to their future self. We do not advocate for one view over the other (deprivationism or TRIA) but rather sketch the different implications of the views.
It’s unclear exactly how TRIA should be represented: two people could hold the view “saving 20-year-olds is better than saving 2-year-olds” but disagree over how to make this mathematically precise.[39] But in terms of the relative moral weights of saving an under-5 to doubling consumption for a year, the basic implication of moving from deprivationism to TRIA is that the relative value of saving under-5s will go down.
(TRIA): WELLBYs lost = (expected well-being level - neutral point) * [(life expectancy - age at death) * discount]
The TRIA discount reduces the value of averting the death of someone younger than the age of full psychological connectedness. We represent this as a simple linear function, discounting from zero at three months before birth and one at the age of ‘full psychological connectedness’ (see Figure 2). We use a range of values between 10 and 21 years for the age of ‘full psychological connectedness’ in our model. The WELLBYs lost directly due to the death of an under-5 under TRIA are then estimated to be 45 (9–110) in Guesstimate. It is plausible that the gradient of the TRIA discount becoming less steep with greater age might better capture someone’s intuition of TRIA.
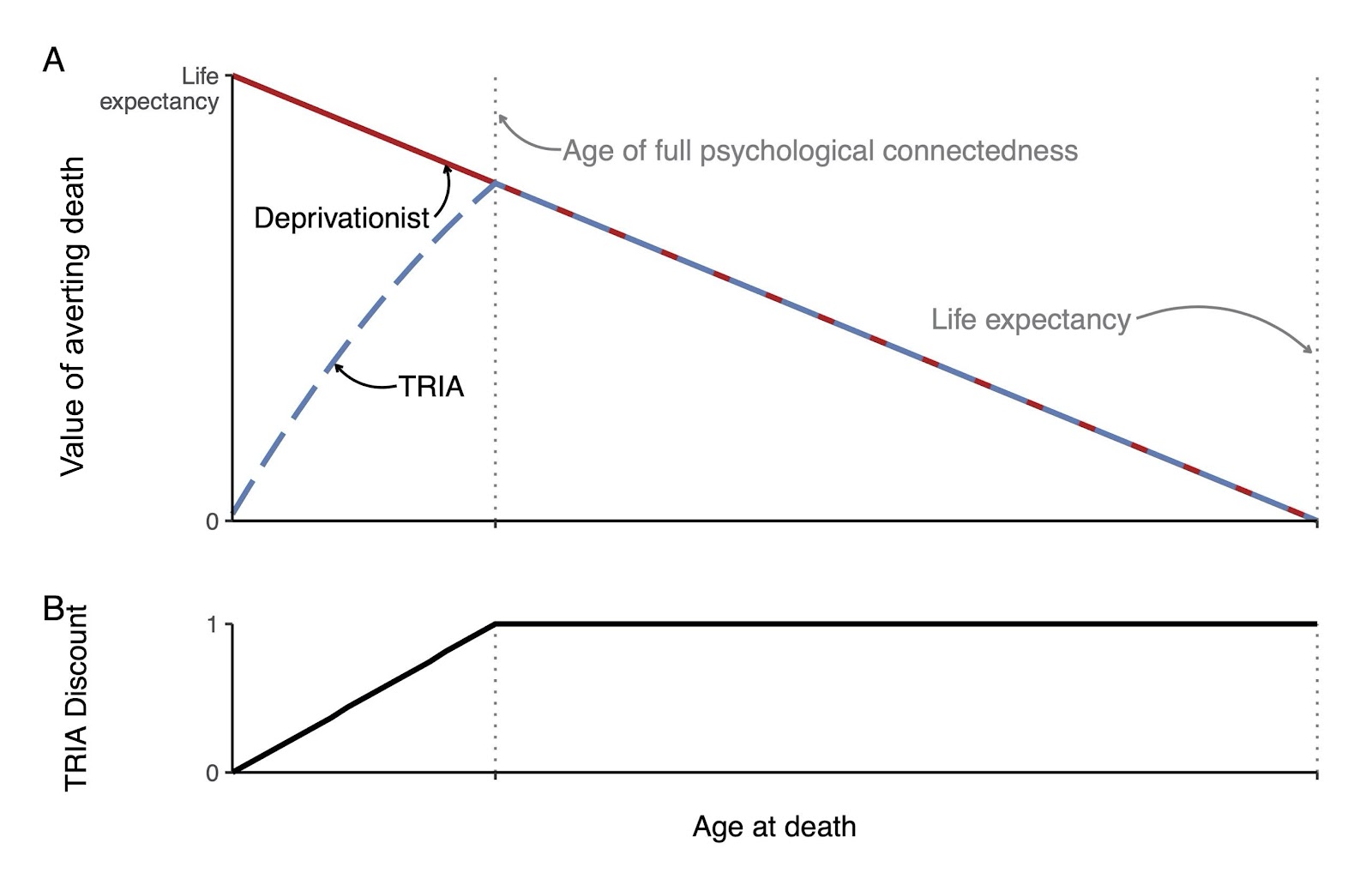
Figure 2: Disvalue of death at a given age, for the deprivationist and TRIA accounts. On deprivationism (red line), the number of years lost at death equals the life expectancy at zero, and decreases linearly as the age at death increases. Our simple TRIA discount function (shown in B) goes from 0 at 3 months before birth to 1 at the age of ‘full psychological connectedness’. This discount is multiplied by the number of years of life left to estimate the TRIA “years” lost due to death at a given age (blue dashed line).We have said that life expectancy is constant.
Spillover effects to household: impact on SWB of bereavement
The clearest effect on the other members of the household due to a death is through grief. The evidence base for the effects of grief on SWB is both slim and predominantly from high-income countries.
In our judgement, Oswald and Powdthavee (2008) is the most relevant study.[40] They use a British panel dataset (generally stronger evidence than a cross-sectional study[41]) and estimate the effect on someone’s LS after the death of their child. The authors estimate the effect of a child’s death on their parents is -0.49 LS points[42] on a 7-point scale (-0.7 points on an 11-point scale). By comparison, the effect of the death of a partner is stronger (but not statistically significantly so) at -0.63 points (-0.9 on an 11-point scale). The sample size is large (n = 28,418), but only 49 individuals reported the death of a child and 89 the death of a partner in the last 12 months, and the standard errors are correspondingly large (0.25 and 0.24, respectively, on the 7-point scale).
Clark et al. (2018)[43] give some indication of the effect through time. Using panel datasets in Britain, Germany and Australia they estimate that the loss of a partner is associated with a drop within the following year of nearly 1 life satisfaction point on a 11-point scale. Life satisfaction for women and men in the three countries usually returns to pre-loss levels over a five-year period. The total average loss is roughly 2 WELLBYs.
Given this, we input a mean value of -0.7 LS points in our model due to grief to one parent, following Oswald and Powdthavee (2008), with wide confidence intervals (-0.2 to -1.7). We model the effect as recovering linearly to baseline over 5 (2–10) years. In the studies, the deaths could have occurred anytime in the last year, so a reasonable approximation is that the measured change in LS is at 6 months after the death. Finally, we say the effect is the same for the other members of the household, to give a rough total estimate of 6 (1–20) WELLBYs for the effect from grief.
The effects of grief would be diminished if we were to include the counterfactual – that grief will also occur when the individual dies at a later point. It seems reasonable, however, to assume that the (more unlikely) death of a child from malaria will have a much larger effect on someone’s grief than the (more likely) case of someone dying from old age.
Further considerations
Our analysis uses SWB data to (re)estimate the values of two outcomes – increasing consumption and averting the death of under-5s – whilst implicitly holding various background assumptions. However, there are other assumptions one could make that would change the analysis, perhaps substantially, that we will briefly mention.
Above, we’re implicitly assuming a person-affecting view of population ethics on which the only lives that matter are those that will exist whatever we do – in slogan form, person-affecting views hold “morality is about making people happy, not about making happy people” (Narveson 1973). GiveWell does not have an official stance on population ethics, and its staff are sympathetic to a range of views.[44] One might instead hold a view like totalism (on which the best state of affairs is the one with the largest sum of well-being of everyone who ever lives) where, saliently, creating happy lives is good. On such views, the value of saving lives would be quite sensitive to the effect reducing child mortality has on maternal fertility. To explain, parents often seek a particular family size and so have fewer total children if the chance of each dying reduces. A report written for GiveWell estimated that in some areas where it recommends charities the number of births averted per life saved is as large as 1:1, a ratio at which population size and growth are left effectively unchanged by saving lives.[45] For totalists, the value of saving lives in a 1:1 context would be very small (compared to one where there was no fertility reduction) as the value of saving one life is ‘negated’ by the disvalue of causing one less life to be created.[46] One would still need to count other impacts in a 1:1 context, such as preventing grief. Person-affecting views will generally not hold these fertility effects are relevant for assessing impact. It’s worth noting philosophers widely agree that population ethics is a notoriously intractable area of ethics where all of the views have some (very) counter-intuitive results. See Greaves (2017) for a review of the different theories and their issues.
Another consideration is that one might take an ‘Epicurean’ view of death. In this case, death is not bad for the person that dies, hence there is no value in saving lives related to the person whose life is saved; of course, grief and other effects would still be counted.[47] On this view, saving lives is unsurprisingly lower in value.
Given this moral uncertainty, one might want to somehow combine different views, weighted by one’s strength of belief in them, although it’s unclear exactly how this should be done and we do not do so here – see Bykvist (2017) for discussion.
The usefulness of SWB metrics is that they are a plausible means of measuring well-being, one that allows us to put the different outcomes that create, extend, and improve lives into a single currency. Determining the value of outcomes is, of course, sensitive to a range of ethical issues – such as how much one values creating lives – besides how to measure well-being. One still needs to have a measure of well-being however those other ethical issues are resolved.
Discussion of model results
We will briefly describe our initial estimates of the relative value of averting the death of an under-5 and doubling consumption for one person for one year. We will compare the results to previous estimates and discuss their uncertainties and sensitivity further.
Our results
Assuming the deprivationist account of the badness of death, the ratio of averting the death of an under-5 to doubling consumption for one household for one year in our model is about 36:1. In other words, doubling the consumption of 36 households for one year would be of approximate equal value to averting the death of one child who is under-5, although with a wide range of uncertainty. According to TRIA, as we have modelled the view, the ratio of moral weights reduces to about 8:1. To get the respective moral weights for doubling consumption for one person for one year, we divide by the average number of household members. The results are summarised in Table 2.

Table 2: Our results.
Comparison to other methods
Having produced our model and its results, the natural step is to compare these to the estimates used by GiveWell. While we can compare the end results - and these turn out to be similar - it is unclear what to infer from this, given the different methods used.
GiveWell’s moral weight ratio in 2018, using the median of their staff members, was 50 (the range was 8 to 100).[48] The deprivationist (for the household) and TRIA moral weights place a relatively lower value on saving a life (36,33,8), while the deprivationist view for the individual places a relatively higher value on saving a life (154). It is hard to comment on this comparison because we only know how some of the GiveWell staff generated their weights.[49]
IDinsight’s beneficiary preferences report provides an estimate of 230 for the moral weight ratio.[50] This is an average from their two preference-based methods, which we describe in turn.
In the first method, IDinsight asked respondents about their own willingness to pay for a (hypothetical) medicine or vaccine to reduce the risk to themselves or to their child of dying from a (hypothetical) disease. Specifically, they were asked how much they would pay to reduce the risk of dying from the disease from 20 in 1,000 to 5 in 1,000 or 10 in 1,000 (randomised) over the next 10 years. This requires individuals to think in terms of small probabilities, which is quite unintuitive.[51] The average willingness-to-pay was $40,763 (nominal USD) to avert the death of an under-5. This is compared to the average annual consumption per capita assumed for the typical beneficiary population throughout the GiveWell model ($286 in nominal USD) to give a moral weight ratio of 140.
In the second method, respondents were asked to take the perspective of a decision-maker in their community and to choose between saving one life (via a hypothetical intervention) and giving a number of $1,000 cash transfers, where the maximum number of cash transfers possible was 10,000, i.e. a value of $10m. The survey found 38% of respondents preferred to save one life rather than provide 10,000 cash transfers (the ‘never switchers’). In Ghana, the median switching point was >9,995 cash transfers (i.e. at least $9 million)[52], which seems implausibly high. IDinsight took the central estimate from their model[53] – 91 cash transfers – as the input for the moral weight, i.e. the beneficiary preference was interpreted as an indifference between saving one life and $91,000 of cash transfers. This gives an estimated moral weight ratio of 319.
IDinsight also provide ‘literature priors’ of the moral weight ratio[54], a median of 145 (minimum in the literature of 10 and maximum of 240). These are based on estimates of the value of a statistical life (from revealed and stated preferences) in the US and extrapolated to the beneficiary population. You can read about other estimates on this GiveWell page. As noted in the Introduction, however, there are general worries about relying on any kinds of preference-based methods as a guide to how people feel during their lives (see Masur et al. 2013).
Uncertainties and sensitivity
Summary of main results in WELLBYs (with 90% confidence intervals):
- Doubling consumption: 7 (2 to 19)
- Deprivationist – averting death of an under-5: 220 (58 to 360)
- TRIA – averting death of an under-5: 45 (9 to 110)
For doubling consumption, the largest uncertainties come from (at least in the parameters of this model, i.e. not including model uncertainty):
The long-run effect of doubling consumption (primarily given by the effect decay rate). This can be answered empirically although RCTs over long time periods are very rare, given the cost and effort involved.
Spillovers to the household. Further work on the effects on other members of the household (not just the cash transfer recipient) seems fairly tractable, and would tighten up the confidence intervals. As mentioned, we have not included the spillover effects on the wider community, but provide a synthesis in Appendix 2. We plan to comment on this further in our forthcoming meta-analysis (McGuire, Bach-Mortensen and Kaiser, n.d.).
For averting a death, the outcome of the deprivationist approach is dominated by the net WELLBY per year of life, which is itself roughly equally sensitive to the average life satisfaction and the neutral point. Improving the estimate of life satisfaction for this population should be reasonably straightforward - we simply need to survey more people. However, there is a great deal of uncertainty around future SWB. The challenge for improving the estimate of the neutral point is that we lack a theoretical understanding of how best to determine this. If the ideal method involves conducting a few surveys, then further empirical work would be straightforward. We plan to conduct more research on this issue in future.
The estimated total grief effect is ~6 WELLBYs, which is relatively more significant for TRIA (~39 WELLBYs lost from the death itself) than the deprivationist approach (~210 lost from the death itself). As mentioned previously, there is little high-quality evidence from relevant contexts.
A further issue for estimating WELLBYs on the TRIA approach is that the view itself is underdetermined: there are many ways to make precise the idea “saving 20-years-olds is better than saving 2-year-olds”. Advocates of the view would want to make a philosophically and empirically informed determination of its details. Nevertheless, we think our assumption gives a reasonable indication of how TRIA advocates might represent the view.
Concluding remarks
We have illustrated one coherent method to estimate the relative values, in a low-income context, of averting a death of an under-5 compared to doubling someone’s consumption for a year. Specifically, we used life satisfaction, a measure of subjective well-being, to assess the value of each outcome in terms of well-being adjusted life years (WELLBYs). The analysis was feasible given the data available, but the relevant evidence was thin in some areas, such as the long-run effects of cash transfers and the effect of grief on SWB in relevant populations. This approach could be straightforwardly extended to other types of life-improving intervention, such as treating depression, reducing chronic pain, or improving education. It can also be reproduced in terms of happiness, rather than life satisfaction, if and when the relevant data exists. We explained the philosophical and empirical considerations our estimates are sensitive to and compared them to some alternatives. We also stated areas where further work would be particularly useful.
Credits
This research was produced by the Happier Lives Institute.
If you like our work, please consider subscribing to our newsletter. You can also follow us on Facebook, Twitter, and LinkedIn
Appendix 1 - effects on SWB from cash transfers in the long-run
Below we briefly describe the most relevant studies we found of the effects on SWB over longer time periods (greater than two years). Each of these studies is different from the GiveDirectly studies (for example, in the nature or size of the CT, or the outcome measured), and there is wide variety in the long-run effects. Given this, we do not feel we have good evidence to update our estimate of the effect through time in either direction.
- Blattman et al. (2018), working paper: $400 grants were provided to help people start skilled trades in Uganda. At a follow-up nine years later, there was no significant difference in a mental health index between treatment and control. Mental health and SWB cannot be used interchangeably, but we think MH measures at least reveal something about someone’s current feelings.
- Galiani et al. (2018): studied the provision of basic housing (so not a CT, but CTs are commonly spent on housing) in El Salvador, Mexico and Uruguay. After 16 months, SWB improved substantially for recipients of better housing but then after eight additional months (on average), 60% of that gain disappears. The authors’ model suggests the effect completely disappears after 28 months (2.33 years).
- Natali et al. (2018): RCT of a program providing bi-monthly $24 transfers (i.e. not a lump-sum transfer) to mothers in Zambia. 0.19 SDs increase in happiness at three years and 0.25 SDs at four years (i.e. increasing through time).
- Lindvqist et al. (2020): a Swedish lottery study (i.e. high-income country) finds the effects on life satisfaction persist for over a decade and show no evidence of dissipating over time.
- Di Tella et al. (2010): using German panel data (also high-income), suggest that the income effect on life satisfaction decreases by 65 % over four years, which, naively, implies the effect of an income shock on SWB will be completely extinguished in around 5 ½ years.
Appendix 2 - community spillovers
Three of the four GiveDirectly studies shown in Table 1 report effects on ‘psychological well-being’ (PWB) indexes to the community. The PWB index contains happiness and life satisfaction questions as well as measures of mental health (for community spillovers, we do not have the life satisfaction results for every study). We perform two multilevel random effects aggregations of the standardized effect sizes, inverse-weighted by standard error with errors clustered at the level of the sample of the standardized effect sizes. Both show no significant spillover effects (95% CI) on measures of SWB and mental health (MH). This analysis is preliminary as there is a large amount of variance in how CTs are implemented and reported and it is unclear whether a synthesis is insightful without a corresponding analysis of likely moderating effects such as size and time.
Figure 3 is a simple aggregation of the GiveDirectly studies in Table 1. Figure 4 includes all quantitative measures of spillovers on SWB or MH we have found, which includes one non-GiveDirectly study (Baird et al., 2013) looking at the impact of monthly CTs on adolescent girls’ GHQ-12 [55] scores. In Figure 4 we convert all effect sizes into Cohen’s d^[The relationship between native effect sizes (Spillover_es) and Cohen’s d is captured in the following pseudo code:
t = (Spillover_es / Spillover_SE),
dt = t * sqrt((1/(Spillover_n / 2)) + (1/((Spillover_n /2 ))) ),
d_se = sqrt(((Spillover_n /2)/ ((Spillover_n / 2)^2)) +
((dt^2) / (2*(Spillover_n / 2)))))
] since the Baird et al., study used the natural units of the GHQ-12 likert scale.
There is some heterogeneity in how spillovers are accounted for. Most spillovers are from within the (treated) village except in Egger et al. 2019, which looks at spillovers across treated and untreated villages.[56] All studies identify the spillover treatment categorically with geographic proximity of a non-recipient to a recipient (usually in the same village) except in the case of “Is Your Gain My Pain” (Haushofer, Reisinger and Shapiro, 2019) where the spillover is formulated as how many recipients live near a non-recipient (proxied by increases in average wealth of the village). Thus it is the only study that looks at the degree of spillover intensity.[57]

Figure 3: A forest plot of the spillovers of Give Directly studies. Standard errors are clustered on the study level to account for dependence. All spillovers are within the (treated) village except Egger et al., which looks at spillovers across treated and untreated villages.

Figure 4: Forest plot of all CT studies that capture psychological spillovers. The lump value ($PPP total) varies between the Baird et al. (2013) follow-ups because the variable is generated from the sum of all monthly cash transfers and it is the only study where the CT was distributed in monthly installments.
Thanks to Derek Foster for significant input. ↩︎
Although in Appendix 2 we plot known community spillover effects and illustrate a preliminary aggregation. ↩︎
See GiveWell’s 2019 cost-effectiveness analysis. ↩︎
QALYs are a measure of health gained, whereas DALYs are a measure of health lost. A review of other differences can be found in Gold, Stevenson and Fryback (2002). ↩︎
Efforts to use SWB: we are only aware of attempts by one of us (Plant, 2019, ch 7), who provides back-of-the-envelope point-estimate assessments of the value saving lives, reducing poverty, and treating mental health. We improve on Plant’s prior estimate of the value of doubled consumption and saving lives in several ways: we draw on a wider range of studies to inform the value of doubling (household) consumption and assess its total effect over time, modelling this as an annual decay; we use a Monte Carlo simulation with 90% subjective confidence intervals to account for uncertainty; and we estimate the badness of death according to two philosophical views. ↩︎
You can edit the inputs in Guesstimate to see how the results vary. The results will change slightly just by refreshing the page, because the simulations are re-run. The large value displayed in a cell is the mean; if you click on ‘Expand’ for any given cell you can view the median (the 50th percentile). These values can be quite different, particularly if the presence of a few extreme values changes the mean more than the median. You can read more about Guesstimate in the documentation. ↩︎
In a back-of-the-envelope-calculation, Plant (2019) p228-9 claims that, as depression and anxiety have a relatively bigger impact on happiness than life satisfaction, and increasing income has a relatively smaller effect on happiness than life satisfaction, the relative values of treating anxiety or depression compared to doubling income is about three times higher using happiness than life satisfaction (which leaves open which has higher cost-effectiveness in absolute terms on either measure). ↩︎
GiveWell prefers to consider consumption rather than income (see Guide to GiveWell CEAs). Consumption includes the value of all items used within a household. For instance, if crops are grown and eaten at home, the value of this would be included in consumption, but not income. However, consumption is more often operationalized as total expenditures rather than the value of all goods consumed. ↩︎
If a study finds a 1-point increase in LS, and the standard deviation is 2 LS points, then the effect size is 0.5 SDs. Standardising like this means you can easily compare the size of effects measured on different scales. ↩︎
Purely cross-sectional work suffers from two drawbacks when we are trying to estimate the total impact of an income shock on SWB. First, cross-sectional estimates have no time component, so we do not know how long the effect lasts. Second, it is non-causal. We do not know how much of this coefficient can be explained by greater satisfaction with life leading to a higher earnings or vice versa. ↩︎
The result comes from 0.36*ln(2) = 0.24 where 0.36 was the log(income) coefficient. The benefit of using a linear-logarithmic model is it allows coefficients to be interpreted as percent change so you can estimate the effect of doubling without knowing the original units (although the larger the change, the poorer an approximation it provides). ↩︎
From Gallup World Poll 2005 to 2012 (Stevenson and Wolfers 2013, p. 601). Stevenson & Wolfers also consider results from the Cantril Ladder, a life evaluation question which asks individuals to imagine a ladder with steps from 0 to 10, where 0 is the best possible life, 0 the worst possible life, and to place themselves on it. In this case, doubling income leads to an increase of 0.25*ln(2) SDs in LS. ↩︎
“The causal effect of log income on overall LS implied by our estimate is 0.38”, which corresponds to 0.38*ln(2) for doubling income. Also see Figure 4 in Lindvqist et al. ↩︎
A recent paper by Ridley et al. (2020) aggregates effects on mental health and psychological well-being from cash transfers. Figure 10 shows the effects per $1000 (PPP) spent. ↩︎
Using a linear regression model (therefore constraining parameter estimates – log(decay rate) and initial effect size – as normally distributed). ↩︎
This is the only unstandardized value for a SD provided in the GiveDirectly studies. ↩︎
Stevenson & Wolfers (2013) appear to have an SD of 2; British Household Panel survey = 1.9; Lindqvist et al. = 1.93, IDinsight beneficiary report = 2.32. Kilburn et al. reports 1.3 SDs of LS on a 1-5 scale. ↩︎
See O'Hare et al. (2013), Bastagl et al. (2019) and the Our World in Data page. ↩︎
In Egger et al 2019, in households with a married or cohabiting couple, one of the partners was randomly selected as the target survey respondent. ↩︎
There is some evidence of different outcomes depending on whether a woman or a man is the recipient of the CT, for example, Haushofer and Shapiro (2016) find significant differences (at the 10 % level) in psychological well-being and female empowerment between female and male recipient households (but no significant difference for any other treatment effects). They illustrate these differences further in Haushofer et al (2019), where they show the effects on psychological well-being appear driven by women. This result meshes with another evaluation of a CTs which found that the impact on SWB is driven by female-led (and responding) households (Handa and Mark, 2014). It is possible that there will be differences for the other members of the household, too, for female and male recipient households. Given the GiveDirectly studies randomly select whether a recipient is male or female, and so results reflect both cases, we have not tried to account for any differences between male and female recipient households. ↩︎
Another working paper based on the experiments studied in Haushofer and Shapiro 2016, 2018. ↩︎
The work that has been done suggests that the relative income effect remains large in lower income settings (Reyes-García et al., 2016). In the case of Natali et al.’s RCT of a CT in Zambia they find “evidence that the relative poverty pathway dominates the absolute poverty pathway in explaining treatment effects” (2018). ↩︎
y = a + b . log(x) + error ↩︎
See the top of page 4 in these notes: “for a linear-log model, the expected change in Y associated with a p% increase in X can be calculated as βˆ · log([100 + p]/100)”. Therefore, the multiplier on the effect of a 75 % change in consumption for a 100 % change in consumption = (log(200/100) / log(175/100)) = 1.24, or 24 %. In Haushofer & Shapiro (2016), the average $709 CT is 37% of annual household consumption ($1,896, monthly is $158). Using the same equation to calculate how to adjust the effect size in this case produces a multiplier of (log(200/100) / log(137/100)) = 2.2. Intuitively, this seems too high and we do not use it in our model. $709 is an average of a small and large transfer; in future, we could obtain the separate effect sizes. ↩︎
It is therefore important to note that the effect ‘on one person’ is really the average effect on a household member (adults and children). In general, we prefer to work at the household level, rather than the individual level, because we do not have a great deal of information about how either baseline consumption or the CT is split up amongst the household. ↩︎
This is akin to how DALYs are used to estimate the burden of disease. See Gamlung and Solberg (2019) for a collection of philosophical essays on the harm of death. ↩︎
Often, “period” life expectancy is reported (see Our World in Data for an explanation). We probably expect life expectancy to rise in the future for most people, which would not be reflected in period life expectancies. This is an advantage of the projected life expectancies provided by the UN. ↩︎
See World Happiness Report 2013. We use 2013 for the sake of consistency because this is around the time period of the Haushofer & Shapiro (2016) study. It does not matter much which year one chooses, for 2019 estimated LS is 4.5. ↩︎
Figure 8, page 42. ↩︎
To demonstrate this, IDinsight assumed that life satisfaction varies with the log of annual consumption per capita. They used three estimates of the regression coefficient, one from their own results, and also from Deaton (2008) and Stevenson (2013). The predicted life satisfaction of the sample in their survey is 3.62, 3.35 and 4.22. See footnote on page 95. ↩︎
E.g. Toby Ord, The Precipice (80,000 Hours podcast transcript can be seen here). ↩︎
Discounting money or assets obtained in the future is sensible, but this reasoning does not necessarily apply to health or well-being. See this Giving What We Can report by Ord and Wiblin. Note that, here, we are considering the effects of programmes occurring today (so discussion of discounting to account for programmes conducted in the future is not relevant). ↩︎
This is calculated by taking Toby Ord’s estimate of a 1 in 6 chance of humanity not making it through the next century and assuming the risk is constant in that period. ↩︎
This is very speculative, but is calculated based on additional risks to the relevant population (e.g. regional catastrophes) being equally as likely as existential risks. ↩︎
Peasgood et al. (unpublished draft) ↩︎
Appendix 6, p94 ↩︎
See Greaves (2019) for a discussion of how the view is underdetermined and the difficulty of finding a plausible precisification. ↩︎
We found one study in a more relevant context: Deaton et al.’s working paper (2009), using cross-sectional data from sub-saharan Africa. The death of an “immediate family member” in the last year is estimated to reduce SWB by 0.1 points (on Cantril’s 0-10 ladder). The effect on happiness appears much larger, although it is difficult to compare because the happiness question was binary (probability of experiencing enjoyment yesterday). We have not updated based on this study, the main reasons being: (1) The survey did not ask if anyone died in their family in the last year due to any cause, only a subset of causes (AIDS, malaria, tuberculosis and childbirth). The claim that the study is comparing people who had immediate family members die in the last year against those who did not does not appear to be true; (2) the results are extremely heterogeneous and errors are not given. (3) It is hard to know how widely people will have interpreted the death of an ‘immediate family member’; it may be quite different to the death of a child. ↩︎
In a panel you can often control for the time-invariant characteristics of the individual, thereby reducing likelihood of omitted variable bias. This doesn't get you to a causal relationship as you still have to contend with time-varying features of the individual, but it's much better than cross-sections where you likely only have poor measurements of a few of the time-invariant features of an individual. ↩︎
By combining the adjusted OLS and IV estimates: death of a partner has an effect of (-0.590 - 0.661) / 2 impact on LS points (7-point scale). For the death of a child it's (-0.556 -0.430) / 2. ↩︎
The Origins of Happiness, p81 (not available online). ↩︎
See this or this document from current or former GiveWell staff members. ↩︎
It if turned out not to be 1:1, then there would be related concerns about whether the Earth was under or overpopulated. See Greaves (2015) and Plant (2019) ch. 2 for discussion of issues of optimum population. ↩︎
See this 2017 blog post on GiveWell’s website for some discussion. ↩︎
While it is common to discuss Epicureanism as a possible view, it is not a common one to hold. See e.g. Cushing (2007) and Rubio (forthcoming) for two of the few (sympathetic) contemporary discussions. ↩︎
See the 2018 CEA: “Value of doubling consumption for one person for one year relative to saving the life of a child under-5 (AMF)” is given as percentages, with the median being 2%, corresponding to a moral weight of 50. In the 2019 CEA, GiveWell uses a moral weight ratio of 100:1, influenced by the IDinsight survey results. ↩︎
Links to the reasoning of some staff members are given in the CEAs, e.g. the 2018 CEA. ↩︎
See p10 and p102. This result is averaged across Kenya and Ghana. There were significant regional differences in results; see section 1 of the IDinsight report for further discussion. ↩︎
IDinsight assessed respondents’ understanding of probability by asking them several questions, such as “Imagine two lotteries. The chance of winning in one lottery is 5 in 1000, the chance of winning in the other lottery is 10 in 1000. Which lottery has the larger chance of winning?” 58% of respondents correctly answered all of the four basic questions the first time. Only 34% of respondents correctly answered a more advanced question: “Which risk of death is larger: 1 in 100 or 2 in 1,000?”. The surveyor then trained respondents, providing additional explanations until they could correctly answer the questions. See Appendix 2 of the IDinsight report for further discussion. ↩︎
Table 28, p 78. ↩︎
A logistic regression model ↩︎
See result on page 28, and further information on p8, footnote 14. ↩︎
The GHQ-12 is a widely used screening tool for common mental illnesses. ↩︎
They did this by comparing control villages near treatment villages to control villages farther from treatment villages. ↩︎
In economics jargon this is known as the intensive as opposed to the extensive margin. ↩︎

A very interesting post! Thanks for sharing.
I understand that the main objective of this post was to demonstrate a proof of concept and not to argue that the WELLBY approach should be used. If you are planning to do some work on the latter I would personally suggest looking closely at the literature around the suitability of using SWB scores in low-income settings. My understanding is that the consensus view amongst economists is that alternative approaches, such as the capability approach or multi-dimensional poverty indices, are preferable to SWB in such contexts. I should say that I’m currently fairly agnostic on this issue and could be swayed either way, which is why I would love to see a review and philosophical discussion of the literature. If HLI is looking to focus on LMICs, I personally think such a review would be important.
One of the main points of contention is that of “adaptive preferences”. The idea can probably be best be summed up in this quote by Amartya Sen:
Of course you can bite the bullet and say that there is no morally significant difference between a highly deprived person who has adapted to their environment and rates themself at a 5, versus someone materially well off who also rates themselves at a 5. This doesn’t seem to me to be an obviously repugnant view to take, but it is something that I think should be discussed.
I should note that it isn’t immediately clear to me to what extent adaptation could be a problem for your analysis in this post. After all, your analysis around the doubling of consumption considers changes in life satisfaction as opposed to say comparing levels between the poor and rich world for the purposes of optimising resource allocation between them. In addition I did find it interesting in your WELLBYs lost from death analysis, that the happiness scores you cite for the LMIC world are pretty low, which might imply that such adaptation hasn’t occurred to a meaningful extent. Even so, I would say that using life satisfaction scores in a low-income context in the first place requires some acknowledgement of the literature that is critical of doing so. Also, when I saw that the IDinsight beneficiary survey estimated the neutral point at 0.56, whilst the UK study found it at 2/10, this flagged to me the possibility of some adaptive preferences at play.
I just want to reiterate that I’m not saying using SWB measures in LMICs is inappropriate, I just think it might be helpful to have greater scrutiny of doing so.
P.S. Apologies if all of the above was entirely obvious to you and you already have / are planning to look into this topic. Also apologies if I have exaggerated the potential scale of the issue - I’m not an expert when it comes to the economics of LMICs by any means. Having said that I can point you in the direction of some relevant reading if you’re interested in investigating further.
Hello Jack, thanks for the comment. As you note, the document doesn’t attempt to address the issues you raised. We’re particularly interested to have people engage with the details of how we’ve done the analysis, although we recognise this will be far too far much ‘in the weeds’ for most (even members of this august forum).
I’d like to reply to your comment though, seeing as you've made it. There are quite a few separate points you could be making and I’m not sure which you mean to press.
You wonder about the suitability of SWB scores in low-income settings and raise Sen’s adaptive preferences point.
One way to understand the adaptive preferences point is as an argument against hedonism: poor people are happy, but their lives aren’t going well, so happiness can’t be what matters. From this it would follow that SWB scores might not be a good measure of well-being anywhere, not just in low-income contexts. Two replies. First, I’m pretty sympathetic to hedonism: if people are happy, then I think their lives are going well. Considering adaptive preferences doesn’t pull me to revise that. Second, as an empirical aside, it’s not at all obvious that people do adapt to poverty: the IDInsight survey found the Kenyan villagers had life satisfaction of around 2/10. That’s much lower than life satisfaction on average in Kenya of around 4.5. A quick gander at the worldwide distribution of life satisfaction scores (https://ourworldindata.org/happiness-and-life-satisfaction) tells you the poorer people are less satisfied than richer ones. The story might be interestingly different for measures of happiness (sometimes called ‘affect balance’).
Another way to understand the force of adaptive preferences is about what we owe one another. Here the idea is that we should help poor people even if doing so doesn’t improve their well-being (whatever well-being is) - the further thought being that it won’t improve their well-being because they’ve adapted. I don’t find this plausible. If I can provide resources for A or B, but helping A will have no impact on their well-being, whereas B will have their well-being increased, I say we help B. (To pull out the intuition that adaptive preferences is really about normative commitments, note we might think it makes sense for people in unfavourable circumstances to change their views to increase their well-being, but that there’s something odious about not helping people because they’ve managed to adapt; it’s as if we’re punishing them for their ingenuity)
A different concern one might have is that those in low-income contexts use scales very differently from those elsewhere: someone who says there are 4/10 but lives in poverty actually has a very different set of psychological states from someone who says they are 4/10 in the UK. In this case, it is mistaken to take these numbers at face value. The response to this problem is to have a theory of how and why people differently interpret subjective scales so you can account for and adjust the score: e.g. determine what the true SWB values are on the same scale. This is one of the most important issues not adequately addressed by current research. I’ve got a (long) paper on this I’ve nearly finished. The very short answer is that I think the answers are (cardinally) comparable and this is because individuals try to answer subjective scales in the same way as everyone else in order to make themselves understood. On this basis, I think it’s reasonable to interpret SWB scores at face value.
Hi Michael,
Thanks for your response. Apologies that I chose to sidestep the actual analysis itself. For what it's worth I was very impressed when I was reading through it. I might revisit at some point to see if there are any specific comments I can provide on the analysis.
Apologies if I wasn't clear. The main point I want to press isn't that I disagree with the use of SWB in LMIC analysis, it's actually just to highlight that, to my knowledge, this isn't the preferred approach of economists to analyse wellbeing in LMICs. Therefore if such analysis is going to feature heavily in HLI's work I personally think it would be worth your while to address this tension formally in some way. This could be by doing a write-up to justify your choice to use SWB rather than say the capability approach or multi-dimensional poverty indices. If you address this formally I think it would increase the probability that the work of HLI is taken seriously by economists, and you may even win over some converts to your cause. If you don't address this I have a feeling many economists (and perhaps some other people of interest) would ignore your work citing concerns over adaptive preferences.
Of course I'm not an expert so if I were you I'd test this with some academic economists. The director of The Oxford Poverty & Human Development Initiative, Sabina Alkire, is a leader in multidimensional poverty and the capability approach. She would be a brilliant person to talk to get a clearer sense of the current views of economists regarding the use of SWB in LMIC. It may well be the case that economists are more accepting of this approach than I realise.
For what it's worth I think that this might be the most prominent concern. I look forward to seeing your paper arguing for cardinal comparability. If your paper covers cardinal comparability between those in low-income and high-income contexts, then I think it would go some way to addressing the tension that I have raised.
Glad you were impressed! Would welcome any suggestions on how to improve the analysis.
Thanks for clarifying. Yes, I understand that economists lean towards a desire satisfaction theory of well-being and development economists lean towards Sen-style objective list theories. We're in discussion with a development economist about whether and how to transform this into an article for a development econ journal, and there we expect to have to say a lot more about justifying the approach. That didn't seem so necessary here: EAs tends to be quite sympathetic to hedonism and/or measuring well-being using SWB, and we've argued for that elsewhere, so we thought it more useful just to present the method.
Oh that's great. I very much hope that goes well! I hope I didn't give the wrong impression from my comments, I would love to see SWB be taken more seriously in the development economics literature.
Detail possible inaccuracy:
While the total study sample size was 1,808 (which is also what the SD refers to), in Kenya 954 respondents were surveyed.
Hi Micheal, great post!
A tangential point I’m confused about.
I’m not sure if we should even account for negative community spillovers, especially if for example we had a taxonomy of different emotions that influence well-being, we wouldn’t count all those as part of our felicifc calculus if they are motivated by e.g. Jealousy. They would be “ill-grounded” An example would be whether or not to account for beliefs about women's inferiority in calculating the benefits (and costs) of suffrage, or disgust with blacks sharing pools when we’re deciding on desegregation. In those cases, I’m okay with ignoring ill-being based on these emotions. But I’m not sure how to deal with edge cases like this.
One way to go about it would be to hold a view where we judge emotions on the correctness of the beliefs they are based on. So in the misogyny and racism cases, the beliefs would be something like women being not smart enough to decide their leaders or that blacks are inherently dirty. And in the GiveDirectly case, we would be okay with the emotions if it’s based on the belief that higher wages for others in the community affect your own purchasing power. (I’m assuming this is true, but I’m not sure). But if the reduced SWB is caused by a false belief (e.g. their neighbors are unworthy), then I don't think we should count them.
Note, that I'm mostly confused about the income spillover effects, the other ones you mention here (e.g. trust) strike me as less problematic. I can also see how only counting "good" emotions and ignoring less positive ones, even if people spend equal amounts thinking them through, would lead to biased results.
Hello SamiM,
It's an interesting position. I'm not sure if it's exactly the same, but it seems similar to desert-adjusted attitudinal hedonism (see here) where certain pleasures/pains don't count if they are(/aren't) accompanied by the right attitudes. I feel the intuitive pull behind it but, on reflection, I don't buy it.
One issue is going to be providing a non-question-begging around of why makes certain emotions, but not others, well-grounded. Does the groundedness related to the emotion? If so, why some rather than others? Does it relate to the beliefs? If so, why is my pleasure only good for me if the beliefs that contribute to it are correct? That doesn't seem relevant at all. This isn't my area of expertise, but I'd be surprised if there was any really good way of doing this.
It strikes me a more plausible way of accounting for the intuitions is that, as a pragmatic matter, we don't want to reward people for being 'bad' (in some, to be specified, sense) lest it gives them incentives to keep doing it. It's an appeal to deterrence, rather than retribution, c.f locking up criminals to demotivate their activities just to punish them for being bad people. On this understanding, you need to actually inform people of your decision-making, otherwise it will just seem, to them, an arbitrary punishment.
In this case, I don't see how deterrence would work here. Would you, um, tell people that you would be giving them lots of money, but now you won't because you've learnt this makes their neighbours jealous?
There are some other issues that spring to mind, but hopefully that suffices!