Thanks - I think this type of careful empirical analysis, and its distillation, is some of the next content on the forum. I found your section on varying parameters particularly helpful for quantifying how sensitive the approach is to these non-empirical inputs.
Executive summary: Epoch's Direct Approach uses neural scaling laws and assumptions about distinguishability to forecast when large language models will reach human-level performance at scientific tasks, which they view as a threshold for transformative AI (TAI).
Key points:
The Direct Approach extrapolates the performance of machine learning models using empirical scaling laws, in contrast to indirect approaches that estimate proxies for performance.
It assumes that if an AI's output is indistinguishable from a human's (accounting for human judges being suboptimal at distinguishing), the AI is as competent as a human at that task.
Combining the Chinchilla scaling law, a distribution over the resources required for indistinguishable performance, and projections of future algorithmic efficiency, compute investment, and hardware improvements yields a forecast of when TAI will be developed.
The model's predictions are sensitive to key uncertain parameters like the "human slowdown factor" and the threshold for indistinguishability. Varying these parameters significantly affects median TAI timelines.
Epoch found inconsistencies in the Chinchilla scaling law. Correcting for these shortens TAI timelines in their model. If valid, this suggests many researchers may be expecting longer timelines than is consistent with the data.
While the model provides a valuable framework, it relies on assumptions like scaling laws holding far outside the range they were measured on. It is intended more as a theoretical framework than a precise forecast.
This comment was auto-generated by the EA Forum Team. Feel free to point out issues with this summary by replying to the comment, and contact us if you have feedback.
Now THIS is forecasting: understanding Epoch's Direct Approach — EA Forum
Now THIS is forecasting: understanding Epoch's Direct Approach
Happy May the 4th from Convergence Analysis! Cross-posted on LessWrong.
As part of Convergence Analysis’s scenario research, we’ve been looking into how AI organisations, experts, and forecasters make predictions about the future of AI. In February 2023, the AI research institute Epoch published a report in which its authors use neural scaling laws to make quantitative predictions about when AI will reach human-level performance and become transformative. The report has a corresponding blog post, an interactive model, and a Python notebook.
We found this approach really interesting, but also hard to understand intuitively. While trying to follow how the authors derive a forecast from their assumptions, we wrote a breakdown that may be useful to others thinking about AI timelines and forecasting.
In what follows, we set out our interpretation of Epoch’s ‘Direct Approach’ to forecasting the arrival of transformative AI (TAI). We’re eager to see how closely our understanding of this matches others’. We’ve also fiddled with Epoch’s interactive model and include some findings on its sensitivity to plausible changes in parameters.
The Epoch team recently attempted to replicate DeepMind’s influential Chinchilla scaling law, an important quantitative input to Epoch’s forecasting model, but found inconsistencies in DeepMind’s presented data. We’ll summarise these findings and explore how an improved model might affect Epoch’s forecasting results.
We’ve accidentally filled this post with Star Wars references. Disclaimer: we do not actually mean to suggest that the Direct Approach is quick or easy (though it is definitely seductive).
This is where the fun begins (the assumptions)
The goal of Epoch’s Direct Approach is to quantitatively predict the progress of AI capabilities.
The approach is ‘direct’ in the sense that it uses observed scaling laws and empirical measurements to directly predict performance improvements as computing power increases. This stands in contrast to indirect techniques, which instead seek to estimate a proxy for performance. A notable example is Ajeya Cotra’s Biological Anchors model, which approximates AI performance improvements by appealing to analogies between AIs and human brains. Both of these approaches are discussed and compared, along with expert surveys and other forecasting models, in Zershaaneh Qureshi’s recent post, Timelines to Transformative AI: an investigation.
In their blog post, Epoch summarises the Direct Approach as follows:
The Direct Approach is our name for the idea of forecasting AI timelines by directly extrapolating and interpreting the loss of machine learning models as described by scaling laws.
Let’s start with scaling laws. Generally, these are just numerical relationships between two quantities, but in machine learning they specifically refer to the various relationships between a model’s size, the amount of data it was trained with, its cost of training, and its performance. These relationships seem to fit simple mathematical trends, and so we can use them to make predictions: if we make the model twice as big – give it twice as much ‘compute’ – how much will its performance improve? Does the answer change if we use less training data? And so on.
If we combine these relationships with projections of how much compute AI developers will have access to at certain times in the future, we can build a model which predicts when AI will cross certain performance thresholds. Epoch, like Convergence, is interested in when we’ll see the emergence of transformative AI (TAI): AI powerful enough to revolutionise our society at a scale comparable to the agricultural and industrial revolutions. To understand why Convergence is especially interested in that milestone, see our recent post ‘Transformative AI and Scenario Planning for AI X-risk’.
Specifically, Epoch uses an empirically measured scaling law for LLMs from Hoffmann et al.’s 2022 study, in which the DeepMind team trained over 400 LLMs with varying amounts of compute and training data to derive the optimal ratio between them – a scaling law. They tested their prediction by building a model called Chinchilla that they claim is compute-optimal, and so the resulting relationship is sometimes referred to as the ‘Chinchilla scaling law’. Epoch uses the Chinchilla scaling law to predict when large language models (LLMs) will reach human-level performance at scientific tasks. The authors selected this performance benchmark as they “anticipate that the most likely way in which a pure software system could be transformative is if it is capable of automating science”.
Next, Epoch makes a crucial assumption:
Indistinguishability implies competence (Δ)
That is, if an AI’s performance at some task T cannot be distinguished from human performance at task T, then Δ tells us that that AI is asgood at T as a human.
The Imitation Wars
To quantitatively measure distinguishability, they introduce a game which, for whimsy’s sake, we’ll call the ‘Imitation Wars’. The game has several variants, but across all of them, you are a judge trying to distinguish between two players: a human and an AI. The players are given a task to perform, and the AI is trying to convince you that it is a human by replicating human performance as closely as it can on the given task.
Version I: The Phantom Marble
In a simple version of the game, the task is to make marbles. You’re given a bag of marbles from one of the players, and you’re asked to figure out whether the AI or the human made the marbles. The key question is: how many marbles do you need to take from the bag and examine to be, say, 90% sure that you are looking at the AI’s marbles, not the human’s?
This number, the number of samples necessary for 90% certainty, is called the model’s k-performance (with respect to the given task). A higher k-performance means the model’s output is harder to distinguish from human output. We’ll stick to more intuitive terminology here, but that’s what it’s called in the paper.
To help you decide whose marbles you are looking at, you’re given a big advantage before you play. You’re allowed to look in both bags of marbles, and you’re even told which bag is which. When it comes time to play, the bags are reanonymised, but you can use your memory of each bag’s respective content and some Bayesian reasoning to help you be a good judge.
Version II: Attack of the Pawns
Let’s consider another task: playing chess. Suppose that both the human player and you, the judge, are chess grandmasters. Most chess games finish in under 100 moves, so if you need to look at 250 moves to confidently identify the AI, then that AI is practically indistinguishable from a grandmaster. In that case, according to Δ, the AI is as good at chess as a grandmaster. Suppose we also know that the AI cost $1 billion and 1020 FLOP to train (with negligible running costs). We can combine all this to get an upper bound: it costs at most $1 billion and 1020 FLOP to build and train a chess grandmaster AI.
“So what?” you say, accusingly. “You built the AI, knew how much it cost, then proved it was a grandmaster and used this to… bound how much it costs to build a grandmaster AI? Big deal.” Well, actually, we can use the scaling law mentioned earlier to turn such measurements into predictions about the cost and arrival date of future AI at specific performance levels; we’ll focus on these predictions later on.
Next, we have to accept and account for the fact that you’re probably not an ideal Bayesian judge. We want an upper bound on the resources required to build an AI whose output is indistinguishable to a human’s. The scaling law that Epoch will use to calculate this upper bound (as we’ll discuss later) is idealised: it relates compute requirements to the total number of moves that would be needed to distinguish between human and AI outputs by a judge who perfectly followed Bayes’ rule. But human judges don’t do this perfectly – only a sith deals in absolute Bayesian rigour – and AI should be considered transformative for humanity when its outputs are of a certain quality from the perspective of humans, not theoretical ideal Bayesians. We therefore need to adjust the scores of the game. How does Epoch do this?
They point out that humans make decisions more slowly than ideal Bayesians do, requiring more evidence to come to a conclusion. Their method for accounting for this human deficit amounts to assuming that humans can only consider some fraction of the available information at a time – for example, you, flawed creature that you are, may only be able to consider the most recent 10% of moves, while an ideal Bayesian judge can simultaneously consider all previous moves. The Epoch team models this by including a fudge factor that we’ll label φ. In the example just mentioned, φ would be 10. Supposing our scaling law tells us that it would take an ideal Bayesian judge 25 chess moves to distinguish between the AI and human players, we then estimate a human judge would take 25 * φ = 250 moves to do the same. This is a better score for the AI; the worse the judge, the longer the AI can fool her for.
The Epoch authors don’t measure or set an arbitrary value for φ, but instead include it as a parameter of their model, and describe in Appendix B of their full report a potential experiment to measure φ.
Version III: Revenge of the LLM
We’ve established the basics of the game Epoch uses to measure indistinguishability, and now we’ll look at how it works for LLMs, like ChatGPT and Claude. Recall that the Epoch authors are trying to predict when transformative AI (TAI) will arise, referring to Holden Karnofsky’s definition of TAI here, which he summarises as:
Roughly and conceptually, transformative AI is AI that precipitates a transition comparable to (or more significant than) the agricultural or industrial revolution.
Epoch also assumes, at least for this model, that TAI will emerge from LLMs:
...in this analysis we assume [that TAI will be] enabled by training an autoregressive model that achieves coherence over sufficiently long sequences of natural text
In particular, they’re interested in the automation of scientific tasks:
we anticipate that the most likely way in which a pure software system could be transformative is if it is capable of automating science
So, how do we adapt the game to measure the science chops of an LLM?
Epoch’s answer is to assess the LLM’s ability to produce scientific papers that are indistinguishable from human-generated scientific papers. Appealing to Δ, they then derive a measure of how good LLMs are at science. The quote above comes from Epoch’s blog post, which also includes a Q&A with more detail on why they use “automating science” as a threshold for TAI, and why “producing scientific papers'' makes sense as “the hardest bottleneck” for, and thus a reasonable measure of, science capability.
In this version of the game, a human scientist and an LLM are both tasked with generating scientific text. Effectively, the bag of marbles in Version I of the game is now replaced by an ordered sequence of letter-tokens which, taken together, comprise a piece of scientific writing. The question is now: how many letter-tokens (i.e. how much text) do you have to examine before you can determine that you’re looking at a piece of scientific writing generated by an LLM?
Note that the tasks of playing chess and generating language have subtle but significant dissimilarities to the marble production task. Each marble examined from the bag is independent from those examined before and after it, whereas the significance of any text depends on the sequence of text that has come before – the words at the start of a sentence or paragraph give you information about what’s likely to come up next. Indeed, that’s how LLMs work, by identifying and exploiting these patterns: “each [letter-]token is sampled from a distribution conditioned on all the text that came before”.
In particular, the Epoch authors model language as a stationary ergodic process. This is a standard simplification that assumes word frequencies don’t change over time; that a long enough sample is sufficient to understand the whole; and that each new word is determined by a fixed number of preceding words (rather than by words arbitrarily far back).
With this, we have our refined game: a scientific writing duel between a human and an LLM. How do we judge indistinguishability? Recall what we did for the chess game: if the judge needs to look at more moves than an average game contains, they’re functionally indistinguishable. So, if we suppose that most science papers are under 100 pages long, and if a judge would require 1,000 pages of scientific writing to distinguish a human scientist and a particular LLM’s output with 90% certainty, then that LLM is functionally indistinguishable from human scientists at writing scientific papers. Therefore, according to our assumptions, that LLM is as good at science as a human scientist, and transformative AI has arrived.
Of course, 100 pages of convincing text is probably not the exact threshold above which we can legitimately say that an LLM’s performance in this game is “practically indistinguishable” from that of a human scientist. But to forecast the arrival of TAI, as we’ll see in the following subsections, it’s necessary to stipulate such a threshold (or at least a plausible range for it to fall within).The Epoch authors suggest one corresponding to the average length of a scientific paper: if an AI can fool a human judge that its outputs were produced by a human scientist for the entire duration of one average-length paper, then it can reasonably be said to be “indistinguishable” from a human scientist (with respect to the task of scientific writing). We might disagree with this choice (for example, perhaps we think a “practically indistinguishable” AI would be able to fool the judge over a larger body of literature, not just a single paper). But whatever we think this threshold should actually be, let’s call it ψ. Epoch includes it as another parameter of their forecast model, alongside our fudge factor φ.
At this point, we have described a game we can play by which we can determine whether an LLM’s performance is indistinguishable from a human’s performance on writing scientific papers. The next step is to translate the findings of this game into compute requirements which are relevant to forecasting the arrival of TAI.
This is where scaling laws come in. Epoch appeals to the Chinchilla scaling law from DeepMind to estimate a linear relationship between an LLM’s training computation and its performance at scientific text generation. (Note that the Chinchilla scaling relationship only tracks the performance of an LLM trained on internet text rather than scientific papers, but Epoch argues that there’s no reason to expect the relationship wouldn’t extend to generating scientific text). This performance is initially estimated with respect to an ideal Bayesian judge, but then adjusted for fudge factor φ, as described earlier.
Armed with this, what Epoch is most interested in is translating threshold ψ into a corresponding training compute threshold for LLMs. The resulting threshold for compute signifies an upper bound on FLOP requirements for training a transformative AI system.
It can be considered an upper bound for a few different reasons. Firstly, there could be better or more efficient ways of performing tasks such as writing scientific papers than what humans currently do. AI systems may therefore be capable of transforming scientific research before being able to perfectly emulate human scientists. Secondly, there may be other routes, besides the automation of science, by which AI systems become transformative. Though the Epoch authors themselves view improvements in scientific capability to be the most likely route that will take us to transformative AI, it is still possible that AI will be capable of transforming society through some other means before it reaches the identified threshold for scientific task performance.
The Forecast Awakens
We now know how to measure an upper bound on FLOP requirements for training TAI. When will AI development reach it?
To see how Epoch generates a forecast, let’s backtrack slightly: recall that the Epoch authors introduced two key unknown variables into their model:
The fudge factor (φ)
The threshold for indistinguishability (ψ)
In Epoch’s interactive model, users can make confidence percentile estimates on both parameters. This generates a lognormal probability distribution of upper bound FLOP requirements for transformative AI. Using the estimates made by the Epoch authors, the distribution of FLOP requirements looks like this:
Probability distribution of FLOP requirements for TAI, before adjustment
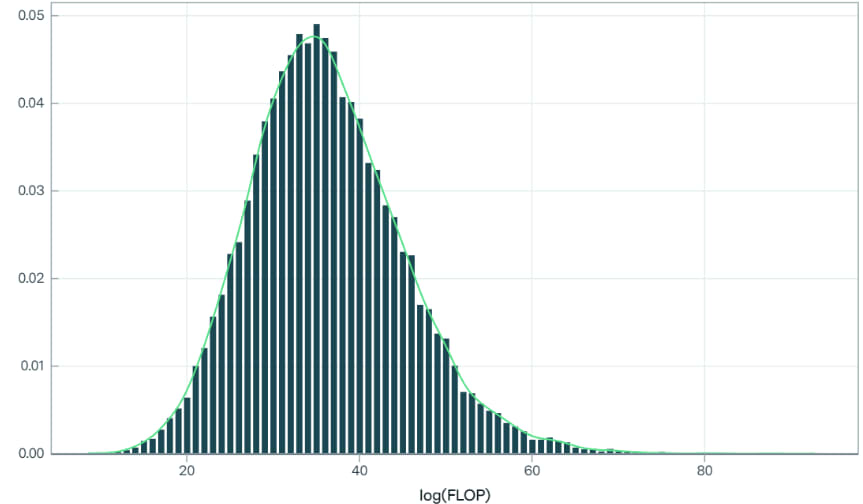
After performing a Bayesian update conditional on TAI not having been achieved from any training runs so far (the largest one to date being to the order of 1025 FLOP) the distribution looks like this:
Probability distribution of FLOP requirements for TAI, after adjustment
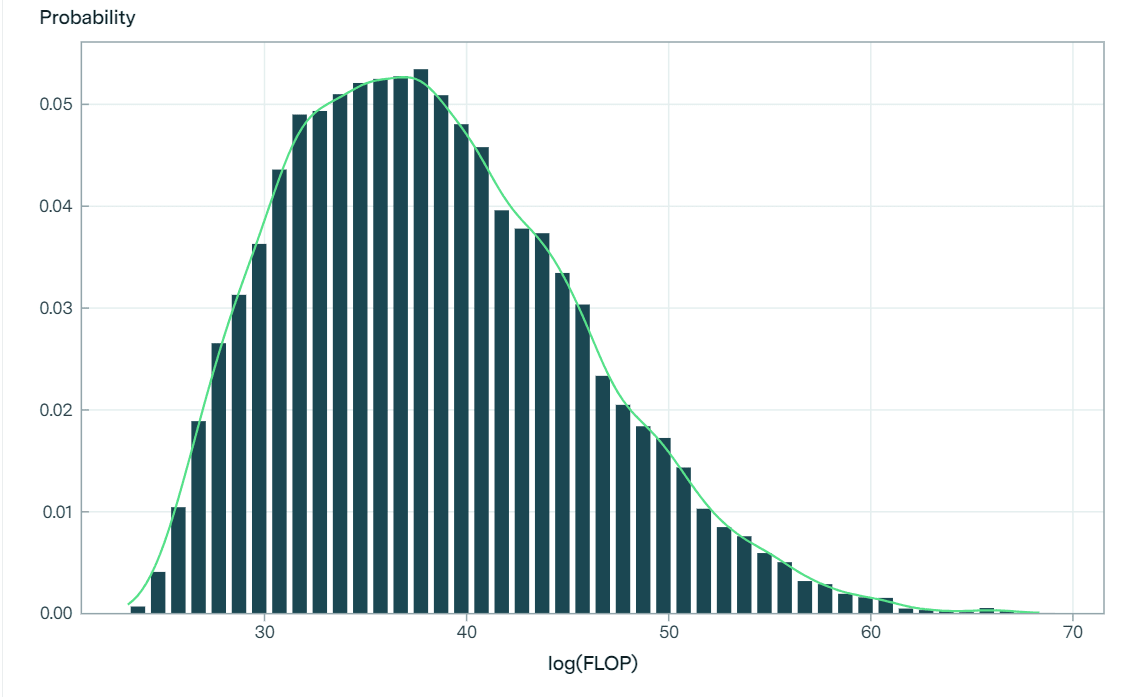
This distribution underpins Epoch’s forecast model, which elicits probabilities of AI being achieved by different dates. Specifically, the Epoch authors combine their distribution of maximum FLOP requirements with projections over time for the three following variables:
Algorithmic efficiency. The present model of FLOP requirements does not yet account for future improvements to algorithms which may enable better performance to be achieved with less training computation. The Epoch authors therefore use projections of algorithmic progress to adjust their upper bound FLOP requirements into the future. To make these projections, they: a) begin with an estimated baseline rate of efficiency improvements for computer vision models (0.4 orders of magnitude per year, from previous work by Erdil and Besiroglu). b) make adjustments to account for “the extent to which [they] … expect progress in potentially-transformative models to be faster or slower than the rate in computer vision” c) set a maximum possible algorithmic performance level, relative to 2023.
Compute investment. Compute costs $$$. So, we need to estimate how much money AI developers will spend on accessing more FLOP for training runs in the future. To do so, Epoch combines “estimates of the dollar cost of current training runs, projections of future GWP [i.e. gross world product] growth, and estimates for the maximum percentage of GWP that might be spent on such a training run”.
Hardware cost-efficiency. How much bang will developers get for their buck (in terms of FLOP per $)? Compute will continue to get cheaper as hardware improves, which will determine when certain compute thresholds become affordable. To account for this, the Epoch authors begin with projections from Hobbhahn and Besiroglu on FLOP/s growth in top GPUs. These projections are adjusted with a “hardware specialisation parameter”, used to account for “future adjustments for specific workloads, including changes to parallelism, memory optimisation, data specialisation, quantisation, and so on”. (The benefits of hardware specialisation are assumed to accrue up to a limit.) This is combined with the estimated cost of a typical GPU to yield projections for hardware cost-efficiency.
b) make adjustments to account for “the extent to which [they] … expect progress in potentially-transformative models to be faster or slower than the rate in computer vision” c) set a maximum possible algorithmic performance level, relative to 2023.
Epoch projects (1) in order to adjust TAIcompute requirements over time, while projections of (2) and (3) are combined to model how much compute developers will have access to over time. Together, this is now enough information to forecast the arrival of TAI.
It’s over, Anakin – I have the results
After assigning percentile confidence estimates to parameters φ and ψ, applying the Chinchilla scaling law, and making the three projections above, the Epoch authors arrive at the following forecast:
Probability distribution over TAI arrival year
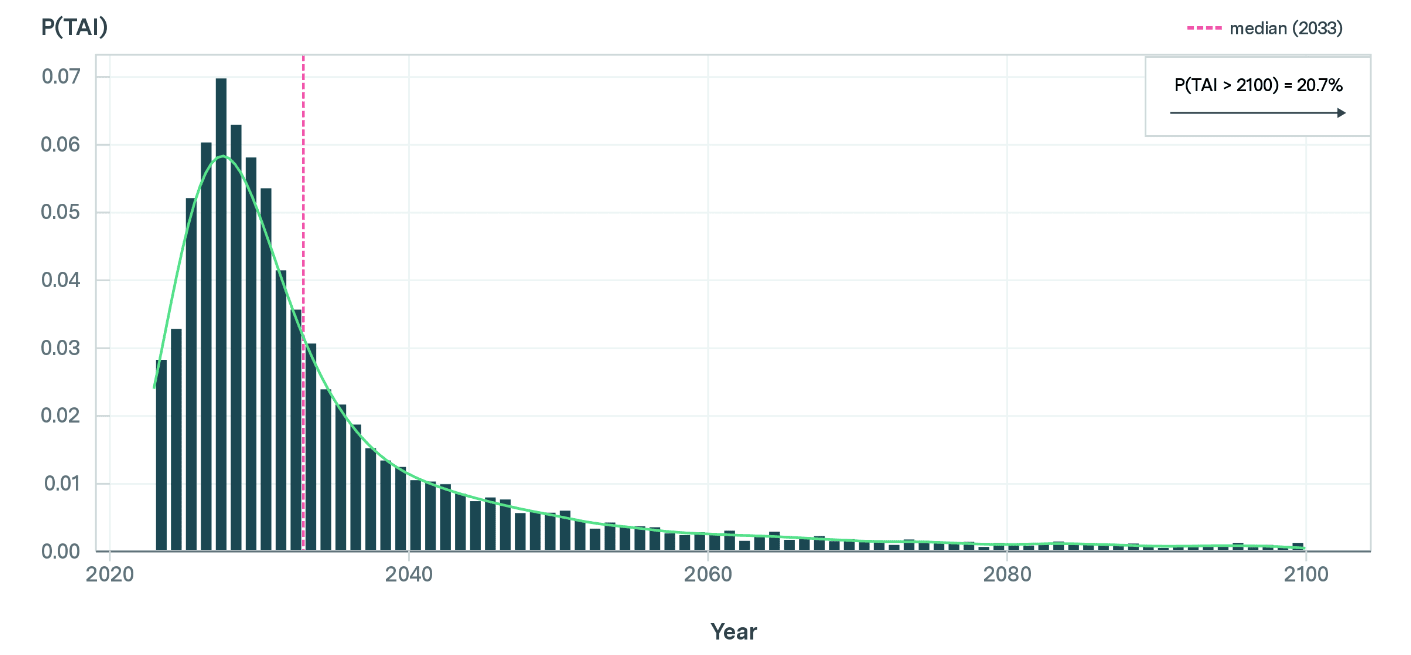
In particular, this model predicts that:
There is a 10% probability of TAI being developed by 2025
There is a 50% probability of TAI being developed by 2033
There is a 79% probability of TAI being developed by 2100.
How sensitive is Epoch’s model to disturbances in the Force?
Epoch has released an interactive model for the Direct Approach, which allows users to adjust the estimated values of some of the model’s variables. The adjustable parameters include the fudge factor, φ (which Epoch labels as the “human slowdown factor”) and the threshold for indistinguishability, ψ (which Epoch labels here as “k-performance”). Users can also make changes to the parameters underpinning Epoch’s projections of algorithmic efficiency, compute investment, and hardware cost-efficiency.
Some of these variables can be set to a precise value, while for others, users can enter 10th and 90th percentile estimates to generate a probability distribution. Functionally, there is limited wiggle room available for making these adjustments; the graph generation tools stall if users try to set values that are too far outside of the original range.
When writing this post, we were especially curious about the effects of adjusting the estimates for φ and ψ on Epoch’s TAI forecast, since there’s a high degree of uncertainty over both parameters. We therefore used the interactive model to try out a few different configurations of the percentile estimates for these parameters.
From a rough review of our results, it appears that the model is fairly sensitive to variations in both of these parameters. Before we go through the numbers, bear in mind that this model is a proof of concept and samples from probability distributions with implicit variability, so these numbers are not static numerical predictions. Nonetheless, here’s some examples of what we found when we fiddled with the parameters:
Fudge factor φ
When we decreased the 10th and 90th percentile estimates for φ from 6.60 and 433 to 5 and 100 (effectively narrowing in on the most optimistic estimates of human judging abilities from Epoch), the median TAI arrival date shifted from 2033 to 2039.
When we made greater increases to the percentile estimates for φ, we observed medians that were several decades later than the original forecast. The most extreme scenario we tested was one in which human judges were confidently believed to be only a few times slower than an ideal judge, assigning a 10th–90th percentile interval of 2–5. This yielded a median TAI arrival date of 2076, a far cry from the original.
Indistinguishability threshold ψ
When we increased both the 10th and 90th percentile estimates for ψ by a single order of magnitude – perhaps corresponding to an assumption that an AI must convince a judge over the length of ten scientific papers rather than just one to be considered “practically indistinguishable” from human scientists – the median TAI arrival date shifted from 2033 to 2057.
[Note: when we made adjustments to these variables in the opposite direction, we observed comparatively minor shifts towards shorter timelines; 2025 was the shortest median arrival date we managed to elicit while varying these parameters. This is because, under its default settings, the interactive model conditions its forecast on TAI not having been achieved yet – i.e. with 1025FLOP, the size of the largest training run to date. As a result, the original median timeline cannot get many years shorter. Epoch has provided users the option to remove this condition, but we have not scrutinised the behaviour of the model without it.]
We don’t have very strong intuitions on what the likely range of values is for either φ or ψ. However, none of the values we tried inputting into the model seemed wildly implausible to us, nor did the adjustments we made to the original estimates span many orders of magnitude of difference – but they ultimately generated wholly different pictures of the future of AI progress to the original model.
What should we make of this? As can be expected from a nascent theoretical model, the predictions resulting from the Direct Approach seem to be fairly sensitive to the values of parameters that are ultimately still uncertain. Refining the estimates for the two parameters above – through empirical testing and further conceptual work – would be especially valuable for improving the predictive utility of the model.
These aren’t the scaling laws you’re looking for
In April 2024, the Epoch authors published a preprint attempting to replicate DeepMind’s scaling law results, an important quantitative input for Epoch’s forecast. Summarising the replication attempts in a Twitter thread, Tamay Besiroglu writes:
The Chinchilla scaling paper by [the DeepMind team] has been highly influential in the language modeling community. We tried to replicate a key part of their work and discovered discrepancies.
The DeepMind team generated the Chinchilla scaling law by fixing either the size of the LLM or its number of training tokens while varying the other, and then modelling the resulting LLM’s success rate. Epoch’s recent experiment attempted to replicate this final modelling stage of DeepMind’s work. As they were unable to obtain the source data directly, the Epoch team approximated it by extracting data from the results graph in DeepMind’s paper, and then fitting their own graph to this reconstituted data set.
The Epoch authors admit there were several limitations to this method as some information was likely lost when the data was graphed in the first place. However, they don’t think these limitations are significant enough to alter their conclusion, noting instead that “Clearly, [DeepMind’s] model does not fit the data.”
In fact, the Chinchilla LLM itself seemingly doesn’t follow the model it was supposedly an example of. DeepMind built Chinchilla with a training-data-to-model-size ratio of around 20 tokens per parameter, but the Epoch team argues that DeepMind’s own model predicts the optimal ratio for an LLM the size of Chinchilla would be 70 tokens per parameter. Instead, Chinchilla is more consistent with the scaling model that the Epoch team built using the reconstituted data:
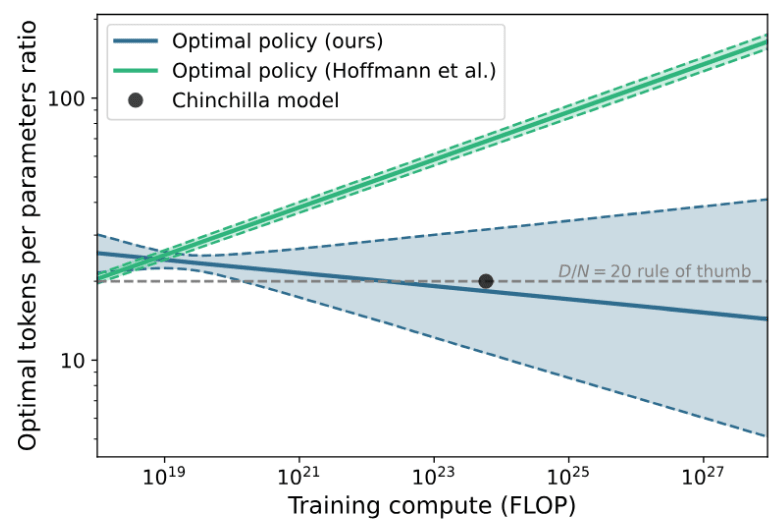
Epoch also found that the DeepMind report was dramatically overconfident in the statistical precision of some of its key variables, writing that “you’d need about 600,000 data points to nail it down that precisely [...] they likely had ~400”.
Any inconsistencies or errors in the Chinchilla scaling law model may have been quite consequential for the many AI researchers who’ve used its results. For the sake of this post, though, we’re interested in how this affects Epoch’s forecast. If we assume Epoch’s new model is more accurate than DeepMind’s, how does this affect the final predictions of Epoch’s Direct Approach?
This information isn’t included in the preprint, but we’ve duplicated the Epoch team’s Python notebook and experimented with it to see how these changes alter the TAI forecasts (see this footnote[1] for details). We had to use this Python notebook to investigate these changes, as the interactive model does not currently allow users to directly edit the scaling law parameters.
Disclaimer: It should be noted here that the workings and outputs of Epoch’s Python notebook do not completely match the interactive model. We suspect that this is due to the use of different estimates for the fudge factor φ and the indistinguishability thresholdψ in each source, as well as differences in the way that the FLOP requirements distribution is generated. The Python notebook thus appears to reflect an alternative version of Epoch’s model with assumptions that differ from the interactive model, which we interpret as a more faithful representation of the Direct Approach. This means that the precise results obtained from our experimentation with the Python notebook should not be interpreted as an updated version of the Direct Approach. Our primary motivation for presenting these results is to give a rough indication of the way we might expect Epoch’s more recent forecast to shift when the authors eventually update their interactive model to use the corrected scaling law parameters (indeed, they have indicated their intention to do this).
With the above disclaimer in mind, we ran the Python notebook first with DeepMind’s original scaling law and then with Epoch’s new scaling law, and found the following:
Epoch’s updated numbers shorten the timeline for the arrival of TAI. That is, the updated Python model assigns higher probabilities to TAI arriving sooner. For example, in the below table, we see a shift in median TAI arrival date from 2054 to 2044.
Relatedly, the updated median compute requirements for TAI are lower than in the original Python model. For example, in the below table, we see a difference of a few orders of magnitude between the two results.
Python notebook with DeepMind’s original scaling parameters
Python notebook with Epoch’s new scaling parameters
Median TAI arrival date
2054
2044
P(TAI) by 2030
10%
19%
P(TAI) by 2050
43%
62%
P(TAI) by 2100
83%
89%
Median compute required to train TAI (to the nearest OOM)
1036
1034
Graphing the cumulative probability distribution for the date of TAI arrival, we see shorter timelines and a slightly sharper rise when we switch to the new parameters (displayed in red):
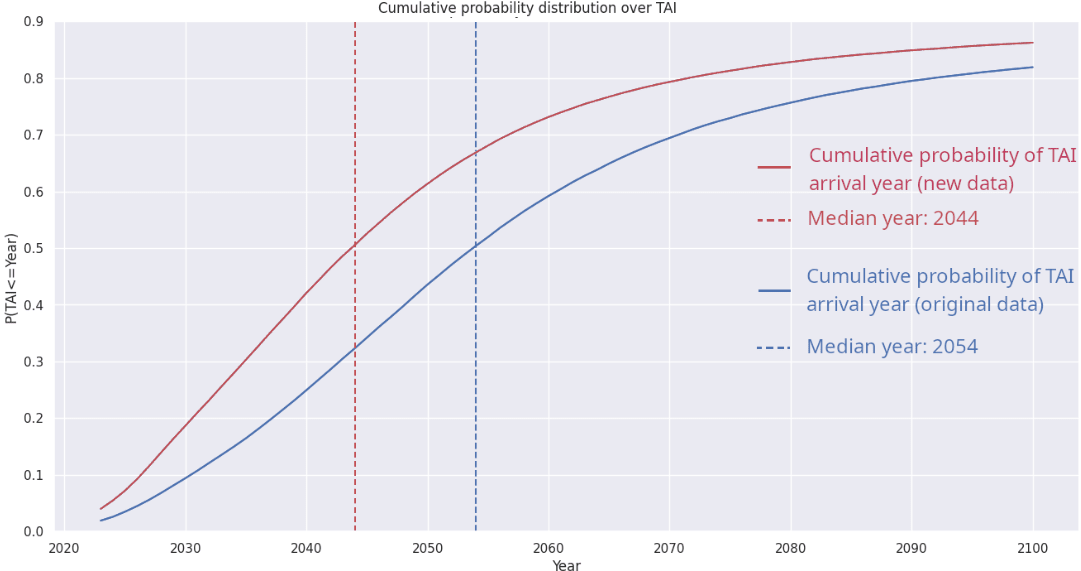
Clearly, Epoch’s model is sensitive not only to the values of the fudge factor φ and the indistinguishability thresholdψ as demonstrated earlier, but also to the parameters underpinning the scaling law; its predictions change significantly depending on precisely how an AI model’s performance is determined by its compute and training data.
Moreover, it is interesting – and worrisome – to find that Epoch’s attempt to correct DeepMind’s scaling law results in shorter predictions for the timeline to TAI. There are a few reasons why we might be concerned by this:
Recall that the current version of Epoch’s interactive Direct Approach model predicts a median arrival date for TAI of 2033, which is already a fairly short timeline to contend with. If applying the corrected scaling law to the interactive model has similar effects to those we observed in the Python notebook, Epoch’s updated version of the Direct Approach could suggest an extremely short timeline to TAI.
DeepMind’s data is much more widely used than Epoch’s reconstructed data, and the Chinchilla scaling law has likely already informed many researchers’ current expectations around the trajectory of AI development. If the Epoch team is right about the numerical errors in this scaling law, these expectations could be seriously misguided; those who have formed beliefs about AI development on the basis of this scaling law may be expecting longer timelines to TAI than is actually consistent with DeepMind’s data.
Is this The Way? (Our reflections)
We think Epoch’s model for forecasting the arrival of TAI has the potential to be extremely valuable. But it does leave us with a lot of questions, some of which are addressed in the FAQs section of Epoch’s Direct Approach blog post. In particular, assuming any numerical errors in DeepMind’s original Chinchilla law paper are resolved, we’re still left with some conceptual questions about the legitimacy of using this empirical relationship to forecast TAI. For example:
Will the relationship identified by the DeepMind team carry over from the context of internet text to scientific text?
Will this relationship hold over many orders of magnitude of compute?
Will it hold beyond certain levels of capability (human-level and beyond)?
Will data become a bottleneck for scaling? And if so, to what extent?
How well will the relationship extrapolate to the performance of LLMs that are much larger in terms of number of parameters?
In thinking about these (and other) possible concerns, we need to bear in mind the intended use of this forecast model. That is: the Epoch authors do not think we should put much stock into any specific bottom line result of the model; as stated in Epoch’s FAQs, its intended use is as “a theoretical framework that can hopefully inform AI timelines”. The model can also be refined as we get more information, such as more relevant empirical data on scaling.
Importantly, the Direct Approach stands as an alternative to popular ‘indirect’ approaches for forecasting the arrival of TAI. As noted in the first section, Epoch directly estimates system performance (based on compute), while indirect approaches such as Ajeya Cotra’s ‘biological anchors’ model instead estimate a proxy for performance. Approaches like Cotra’s have been criticised for relying on shaky analogies between biological and machine intelligence, which direct approaches avoid.
It should be noted that, although Epoch takes an approach to forecasting TAI that is quite different to others in this space, its resulting probability distribution is not vastly dissimilar to those produced by other influential models. Under the current version of the interactive model, its median prediction is just two decades earlier than that from Cotra’s forecast. This adds to a wide pool of recent predictions which suggest that humanity could face transformative AI within the next few decades (and possibly much sooner).
The sacred texts!
If you’re interested in reading more about forecasting in the AI x-risk space, check out these recent posts from the AI Clarity team at Convergence Analysis:
Scenario planning for AI x-risk by Corin Katzke, which highlights the difficulties of making predictions in the domain of AI x-risk, and motivates and reviews methods for applying scenario planning to AI x-risk strategy.
Timelines to Transformative AI: an investigation by Zershaaneh Qureshi, an overview of the current landscape of TAI timeline predictions, including an examination of both Epoch’s Direct Approach and Cotra’s biological anchors model.
We hope this has been a useful and intuitive look at Epoch’s Direct Approach. We’re interested to know what people think about this approach to forecasting and about AI timeline forecasts in general. Which techniques are most promising? Which are most neglected? With whom is the Force strongest?
Thank you to Tamay Besiroglu, Associate Director of Epoch, for his feedback on this post, and to our own Justin Bullock and David Kristoffersson for their suggestions and input.
where N is number of parameters, D is number of training tokens, and E is irreducible loss. Note that the Epoch team chose to exclude five data points from their reconstructed dataset (see Appendix 1 of their paper for the reasons why). For completeness, here is an ugly table of the three different parameter values and their standard errors (with some rounding):
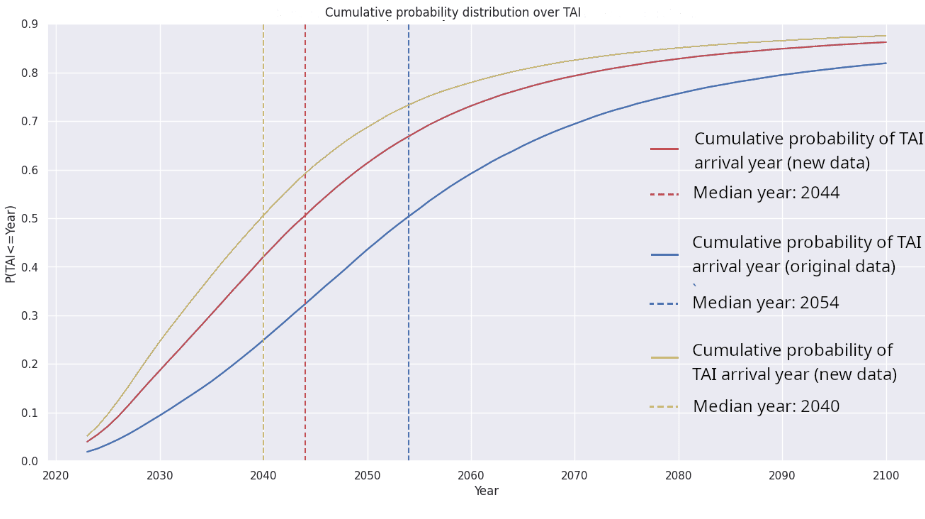
Variable
DeepMind’s original scaling parameters
Epoch’s new scaling parameters (outliers omitted)
Epoch’s new scaling parameters (outliers included)
Value
S.E.
Value
S.E.
Value
S.E.
A
406
25
482
124
463
145
B
411
25
2,085
1,293
12,529
61,557
α
0.34
0.05
0.35
0.02
0.35
0.04
β
0.28
0.05
0.37
0.05
0.45
0.02
E
1.69
1.82
0.03
1.89
0.04
Running the Python notebook with each of these three data sets, we find the following values for the probability of TAI arriving by 2030, 2050, and 2100, and the median year we’d expect to see TAI. In summary, Epoch’s new values mean shorter timelines – TAI is more likely to arrive soon – and, if the outliers are not omitted, much shorter timelines.
Python notebook with DeepMind’s original scaling parameters
Python notebook with Epoch’s new parameters (outliers omitted)
Python notebook with Epoch’s new scaling parameters (outliers included)
Epoch’s interactive model (Direct Approach) with DeepMind’s original parameters
This is the third in a sequence of posts taken from my recent report: Why Did Environmentalism Become Partisan?
Summary
Rising partisanship did not make environmentalism more popular or politically effective. Instead, it saw flat or falling overall public opinion, fewer major legislative achievements, and fluctuating executive actions.
Public Opinion...
This post presents the executive summary from Giving What We Can’s impact evaluation for 2025. At the end of this post we share links to more information, including the full report and...
Thanks - I think this type of careful empirical analysis, and its distillation, is some of the next content on the forum. I found your section on varying parameters particularly helpful for quantifying how sensitive the approach is to these non-empirical inputs.