This is the first of a three-part series of posts from me and Ben Snodin with input from Phil Trammell summarising, critiquing, and suggesting variations on Leopold Aschenbrenner's Existential Risk and Growth (2019).
- This first post gives an overview of the model and results of the paper.
- The second post will discuss how seriously to take the conclusions that follow from the model, highlight some of the more robust conclusions, and discuss objections to the model.
- The third post will outline directions of further research that we believe to be most promising.
The series should be useful to anyone interested in understanding existential risk, in particular:
- Those interested in how economic growth influences existential risk;
- Those thinking about whether we can find useful insights about the complex systems that determine existential risk through relatively simple, abstract models.
Hopefully we'll demonstrate that this kind of research is a fruitful way to get insights about existential risk, and others will be motivated to improve on the existing paper. The series assumes understanding of basic calculus but no formal economics knowledge.
Summary Outline
Section 1 - Setup introduces a model of an economy containing a consumption sector and a safety sector. Section 2 - Allocations explores the very long-term behaviour of this economy for two different cases: a fixed allocation of labour across different sectors, and a variable allocation determined by the preferences of the population. Section 3 - Transition Dynamics looks at how this economy behaves at intermediate times when the allocation between sectors is determined by the preferences of the population.
The results of the model are that civilisation may be going through a ‘time of perils’ in which it is rich enough to have the advanced technologies that threaten its survival, but is not yet rich enough to be willing to spend sufficiently on mitigating these risks. It might then be prudent to minimise time spent in this time of perils—by preventing economic stagnation, or accelerating economic growth. In light of this result, Section 4 - Patience vs. Growth compares the impact on existential risk of making the population more patient with the value of making the population wealthier.
1. Setup
This section builds a model of an economy including population, safety, consumption, and existential risk. We will then see how this model evolves over time.
Population
We model the economy as containing two sectors—a consumption sector, and a safety sector. There are consumption goods which people buy and consume to increase their welfare. There are safety goods (such as pollution mitigation, nonproliferation treaties, or pandemic preparedness programs), which reduce the risk of catastrophe. Each person in the economy works in either the consumption sector or the safety sector. People employed in a given sector can be workers or scientists. Workers produce goods for their respective sector. Scientists produce technologies for their respective sectors.

We can define labour allocation variables for this system:

Where is the total population, is time and the subscript indicates that the variable is a function of time.
Labour Allocation Variables
There are three questions we can ask for this model:
1. What is the fraction of scientists at time t working in the consumption
sector? (The other scientists are in the safety sector.)
2. What is the fraction of workers at time t working in the consumption sector?
(The other workers are in the safety sector.)
3. What is the fraction of people at time t working as scientists? (The other
people are workers.)
So our allocation variables are , , and . These are all the variables that can be controlled in the model.
Production Functions
We assume that the production of consumption technologies, , and safety technologies, , are governed by these equations:
,
.
Where and are constants, and . This is just to say that technological progress has diminishing returns in scientists and existing technologies. We assume that the production of consumption goods, , and safety goods, , are governed by these equations:
Where . (In the current version of the paper, there are slightly different production functions. These give similar results but add unnecessary complication. My understanding is that the will be changed to the functions presented in this summary.)
Similarly to the labour allocation variables, we can define per capita variables for production in each sector and .. We assume a rate of population growth that is exogenous to the model so that: .
Existential Risk
Consumption goods increase welfare -which is great. But they can also increase the probability of existential risk -for example, by more carbon emissions, more powerful AI systems, or more dangerous biotechnology. This risk depends on the total amount of consumption goods being produced, and the risk mitigation depends on the total amount of safety goods being produced.
Risk of catastrophe at a time is given by:
Where is a constant, is the production in the consumption sector, is the production in the safety sector, is the potency of consumption goods on increasing existential risk, and is the potency of safety technologies on reducing existential risk. This formalizes the idea of `differential technological development': existential risk depends on the rate of development of potentially dangerous technologies relative to technologies that ameliorate these hazards.
Therefore, the probability of civilisation surviving to time is given by:
This is useful to consider for two reasons. Firstly, by considering the limit as , we can see the probability that civilisation never destroys itself:
.
This probability is only non-zero if is finite. So instantaneous existential risk has to decrease quickly enough over time or civilisation will destroy itself eventually. The second reason this is useful is because of the role it plays in agents' actions. This is discussed in the next section.
Agent utility
If we first find the utility function of a representative agent in this model, we can then see how that agent would allocate labour to maximise her own utility. Then, if people in the world collectively allocated labour in accordance with their preferences, the results of this model indicate real world labour allocation. A representative agent cares about their own instantaneous utility ut which depends on their consumption at time at that time ct. However, they discount this utility by two things:
1. A survival probability - future consumption is less valuable than present
consumption because of uncertainty about whether civilisation will survive;
2. A discount factor - people behave as is they value welfare now more than
welfare later.
So agents will want to maximise this utility function:
Form of the Utility Function
We assume a utility function of the following form:
is a constant normalising the utility of death to zero. The second term has constant elasticity in consumption (unless ). So increasing by some fraction always increases by some other fraction .
This means that the total utility, including , has constant elasticity of marginal utility of consumption. So multiplying by some small fraction always multiplies by some other fraction .
is a parameter that measures people’s preferences about risk (the coefficient of relative risk aversion). If then the preferences associated with the utility function are risk neutral (so twice as much consumption means twice as much as utility). For higher values of , the value of life relative to the value of marginal consumption is higher. For these cases, an increase in wealth will create more demand for safety relative to consumption.
[Edit: this section incorrectly said the the whole utility function has constant elasticity in consumption, which isn't true - only the second term has constant elasticity in consumption. The whole utility function has constant elasticity of marginal utility in consumption.]
2. Allocations
The allocation variables , , and could either be set at some fixed levels, or they could be allowed to vary to represent agent’s shifting priorities as the system evolves. The first case isn’t particularly realistic and, in short, in the fixed allocation, we find that:
1. If , the hazard rate falls exponentially and ,
2. If , the hazard rate δ increases exponentially and ,
3. If , the hazard rate converges to a constant and .
This highlights the crucial role of the value - it represents the scale effect of existential risk, or the fragility of civilisation. If then increasing the size of the economy while keeping labour allocations constant will reduce existential risk. And if then increasing the size of the economy while keeping labour allocations constant will increase existential risk.
Optimal Impatient Allocation
As people grow wealthier, the marginal utility of consumption declines, and it becomes relatively more valuable to purchase more life and spend on avoiding death. In this model, agents are able to do this through spending on the safety sector. This section explores how agents might allocate variables for different values of .
Constrained Optimisation
[This section is a bit technical, so feel free to skip to the results, starting with 'Robust World'. Though if you are interested, I’ve written up an explanation of how to use Hamiltonians for systems like these here.]
We want to find the path of , , and that maximises
subject to the constraints of the technology production functions, and the survival probability:
.
Where the overdot indicates the derivative with respect to time. To find the path that optimises U subject to our constraints we can define a Hamiltonian H:
Where are Lagrange multipliers. Then the optimal path of , , and is characterised by the following conditions holding at all times:
,
,
,
,
,
.
subject to the boundary conditions:
,
,
.
These are the conditions solved in the paper, and the results are presented below.
Robust World
If , so that existential risk falls with scale, then as long as there is growth, and the proportion of resources going to safety does not decline exponentially or faster (which it will not, even along the impatient-optimal path), risk decreases. Furthermore, exponential growth will produce an exponential fall in the hazard rate, and a positive probability of avoiding existential catastrophe.
Fragile World
If , so that existential risk grows with scale:
1. the relative value of life rises as consumption grows. So does risk, but
labour is moved from consumption to safety quickly enough that declines
quickly enough. Unlike in the fixed allocation, there is a positive, nonzero
probability that humanity does not succumb to an existential catastrophe -
2. If , the relative value of life is slightly less. Labour is still shifted towards
safety, but not quickly enough for the hazard rate to decay - .
Hyper-Fragile World
If then there is no safe allocation on the optimal path. Even if almost everyone works on safety, civilisation will destroy itself eventually. The condition for this is that , which can be interpreted as the scale effect of existential risk being greater than the scale effect of ideas.
Note that, if then there is no desirable allocation, not even from a fully patient perspective, that causes δ to decay quickly enough for . To lower existential risk quickly enough, labour must be shifted so far from consumption to safety that instantaneous utility falls below -rendering death preferable to life.
3. Transition Dynamics
So far, we have looked at what state the system tends to for large values of time. But we are probably far from this long-run result. To understand the relationship between growth and risk today, we need to look at how the system changes as it moves towards the steady state. We’ll look at the impatient optimal allocation for the case because this seems like the most action-relevant case. If then there is no safe feasible allocation of labour, and if then, as long as there is some growth and safety spending, . Also, the case is perhaps the most likely. Too see this, consider that both anthropogenic existential risk and safety spending seem to have increased over time, suggesting the scale effect of existential risk is positive.
To get a sense of the qualitative dynamics of the system we have to pick some parameter values. These values, and evidence for them, are discussed in the paper, which also says that other values produce similar results. We’re particularly interested in the behaviour of the instantaneous hazard rate over time. The hazard rate follows an inverted U-shape. It starts at a relatively low level, but then grows with scale. At the time representing today, is much higher than it was hundreds of years ago. However, as consumption grows, the value of extra life increases and so resources are shifted to safety. This slows the growth of and eventually causes it to decrease. Note that this is analogous to other empirical trends we’ve observed, like environmental degradation (and perhaps meat consumption) where, when people are poorer they are more willing to tolerate some bad thing if it makes increasing consumption easier. Then, as they become wealthier, they value reducing the bad thing relatively more than they did before.
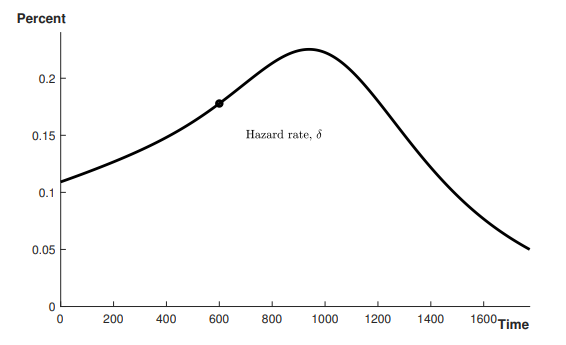
Acceleration
Imagine we increase growth for a period of 30 years and then it goes back to its previous steady level. E.g. imagine annual population growth goes from its usual value of 1% to a higher rate of 2% for 30 years, before going back to 1%.

The effect of accelerated growth for a period of time is to make people richer earlier, so they sooner value life relatively more, so they sooner spend more on safety. This means that the overall area under the hazard rate curve is lower, so the total probability of existential catastrophe over time is smaller. The reverse happens when growth decelerates. Society is stuck with higher levels of risk for longer. So slower growth, even just for a while, might not just mean lower living standards, but perhaps also significantly smaller chance of civilisation’s survival.
Transitory Boom
Imagine we increase growth for a period of 30 years and then it goes back to a lower value for some time such that the overall growth was the same as if the boom hadn’t happened. In particular, imagine that annual population growth goes from its usual value of 1% to a higher rate of 2% for 30 years, before going all the way down to 0% for 30 years, and then eventually back to 1%. What will the effect on hazard rate be? In this case, growth rates of technologies and consumption are the same after the boom as they were before. The allocation between sectors is the same after the boom as the relative value of life is the same after the boom.

The trajectory of the hazard rate after the boom is the same as without the boom. But in the process of the boom there was increased existential risk. Unlike the acceleration case, this temporary increase in risk came with no long-term decrease in risk. Simply “juicing” growth for a while may actually backfire, reducing the probability of humanity’s survival. The opposite occurs for a transitory bust—the hazard rate curve is perturbed downwards and then returns to its previous trajectory.
4. Patience vs. Growth
Safety can be increased by increasing consumption (so people are richer, and value life relatively more), or by reducing their rate of pure time preference (so they value future welfare relatively more). If we want civilisation to demand more existential risk mitigation, should we prioritise economic growth, or moral longtermism? This depends on γ and the relative value of life. For a higher relative value of life it needs more and more consumption to increase safety-focus so economic growth becomes less effective at reducing existential risk. The table below shows, for different values of , what the elasticity of concern for safety in ρ is (i.e. how sensitive concern for safety is to changes in the discount rate). For comparison, the third column shows what ρ would have to be reduced to from its original value of 2% to match the increase in the concern for life from doubling consumption.

Conclusion
From the paper:
‘Technological development can create or mitigate existential risks...humanity may be in a critical “time of perils.” We may be economically advanced enough to be able to destroy ourselves, but not economically advanced enough that we care about this existential risk and spend on safety. This “time of perils” implies that working on reducing existential risk now could be very impactful from an altruistic perspective. Faster economic growth, while initially increasing risk, can help us get through this “time of perils” more quickly and thus increases the long-run probability of humanity’s survival. Conversely, short-term economic stagnation could substantially curtail the future of human civilization. Even if you care only about the long-term future of humanity, the pace of economic growth in the short run could be key to whether we make it there.’

Leopold has now published a popular article discussing this topic. Highly recommended.
An excerpt:
Thank you for producing this! I'd love to see more such summaries of EA research papers, even if the authors don't go so far as to use LaTeX (though that's a nice bonus).
Thanks for writing this up! It sparked some good discussion here at CEA.
This paper claims that CRRA (γ) is around 1. According to the table in the article (p13 in your summary), if γ=1.1, then we are indifferent between decreasing the discount rate from 2% to 1.87% versus doubling consumption.
I admit that I have a very poor model of how hard it is to decrease someone's discount rate, but it seems massively easier to decrease people's discount rates by 13 basis points versus doubling consumption. Are my intuitions really off about that?
If I'm right, it seems like this model pretty clearly argues for spreading longtermism versus economic growth.
Great to hear this has been useful!
I think if γ is around 1 then yes, spreading longtermism probably looks better than accelerating growth. Though I don't know how expensive it is to double someone's consumption in the long-run.
Doubling someone's consumption by just giving them extra money might cost $30,000 for 50 years=~$0.5million. It seems right to me that there are ways to reduce the discount rate that are much cheaper than half a million dollars for 13 basis points. Eg. some community building probably takes a person's discount rate from around 2% to around 0% for less than half a million dollars.
I don't know how much cheaper it might be to double someone's consumption by increasing growth but I suspect that spreading longtermism still looks better for this value of γ.
How confident are you that γ is around 1? I haven't looked into it and don't know how much consensus there is.
I just looked at the one paper. I'm not sure if other sources disagree.
Even if γ was 2 though, I still feel like it would be cheaper?
It's hard for me to think about changing individuals, but if I think of governments: there some government department which is responsible for the welfare of some population. We have 2 options:
Surely the first one is easier? If only because it's at least in principle possible – even if the US government would magically do whatever I said, I don't know if I could suggest a policy change that would double consumption.
Yeah, that seems right to me.
On doubling consumption though, if you can suggest a policy that increases growth consistently, eventually you might cause consumption to be doubled (at some later time consumption under the faster growth will be twice as much as it would have been with the slower growth). Do you mean you don't think you could suggest a policy change that would increase the growth rate by much?
That's a fair point. I guess the thought experiment could be something like: the department is responsible for some set of people's welfare 50 years from now. We have to either convince that department to have a lower discount rate 50 years from now, or adopt some measures such that the people born 50 years from now will have doubled the consumption (relative to the counterfactual)?
If that's right, the discount rate thing still seems easier. It seems hard to double consumption over a 50 year period, though definitely easier than doubling it immediately.
Automated note: This post mentions the paper "Existential Risk and Growth". That paper has been evaluated and rated by The Unjournal. Expert evaluations and ratings can be found at unjournal.pubpub.org.