Epistemic status: I am quite worried this is a very obvious point that doesn’t need its own post. However, I've never seen this point made in this way on the forum, and it seems like it might advance a difficult debate. So I hope that at the very least spelling out the obvious is useful in that sense!
As I understand the state of the near-term vs long-term debate in EA, your view on the discount rate (almost) entirely determines whether you should be a longtermist or not.
Here is a sketch of the longtermist case as I understand it: “There is a lot of suffering in the world now which we could avert by using scarce resources, but if instead we used those resources to avert future suffering (especially but not exclusively suffering related to existential risk) we would have much greater bang for our buck. This is because we expect the human population to multiply significantly [1], and hence while the best imaginable near-term intervention might help a few hundred people, interventions which prevent future suffering will help trillions of people. While we accept that there may be a case for discounting the value of future lives, the key beats of this argument are unaffected since we’re not talking about even the same order of magnitude of impact when we talk about near- vs far- term”.
The table below rigorously models this statement, showing the total value of all possible future human lives under different rates of increase in happiness and discount rates. The numbers are indexed to our current happiness – so for example if the total happiness in the world is currently a million QALYs, the total happiness that will be generated is a ‘67’ scenario is 67 x one million, or 67 million QALYs. Cells shaded in blue are ‘effectively infinite’ – although they have a finite value in principle, in practice the number is so enormously large we should immediately drop what we are doing and become a long-termists if we think we can make these near-infinite QALY streams even a fraction of a percent more likely to come about.
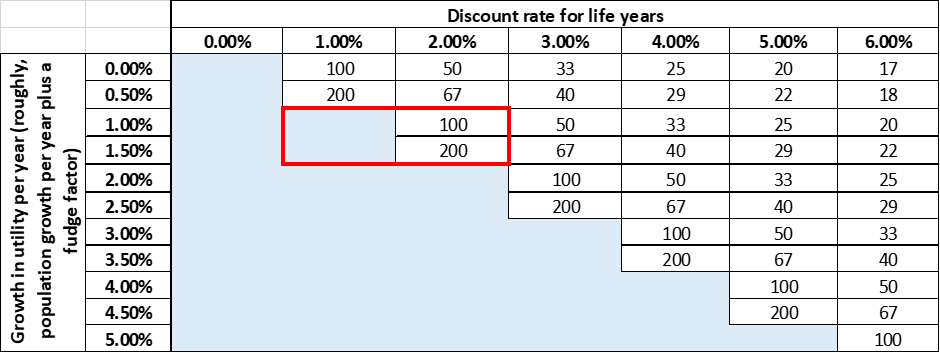
NB The type of analysis here is 'threshold analysis' - I wrote an essay about alternative approaches to uncertainty as part of the Red Teaming contest and you may be able to spot that there are ways to improve this analysis by applying more of those techniques to the problem. This post is just a sketch of the topic rather than a full analysis of the solution under uncertainty!
Three relevant points that come out from this table:
- There is a definite and sharp threshold where you are functionally ‘forced’ to be a long-termist. Specifically, this is where the rate of growth of happiness is greater than or equal to the discount rate, and so the total happiness in the future is effectively infinite. At any discount rate greater than this, the choice of near- vs long-termism depends on the specifics of the intervention being considered. This is interesting because hard discontinuities are inherently quite interesting – very tiny changes in your belief can lead to enormously outsized effects on how you live your life.
- The actual values we assign to ‘growth in happiness’ and ‘discount rate’ aren’t actually that important; what matters is the difference between them. A world where happiness grows at 3% per year but future happiness is discounted at 1% per year is the same as a world where happiness grows at 2% per year but we don’t discount. I've seen a lot of people argue about the discount rate without realising that they need to simultaneously argue about the rate in growth of happiness for the statement to be meaningful as a guide to action on longtermist vs neartermist philanthropy.
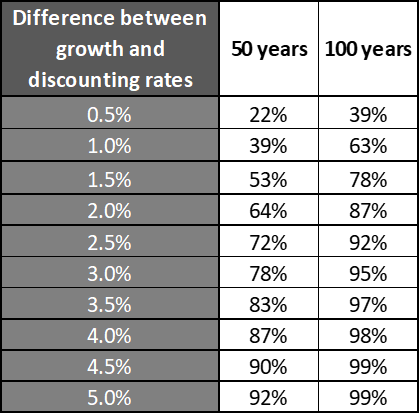
- In keeping with the economics literature, I’ve used exponential discounting in the table above, meaning that QALYs are being ‘front-loaded’ [2]. So for example in a scenario of a 1% growth rate, 2% discount rate we can calculate that 63% of all benefits accrue in the first hundred years (and 39% in the first fifty years). The table below shows how the delta between growth and discount rate affects the percentage of benefits accrued in the first 50 and 100 years. This is relevant to the long-termism debate, because long-term interventions are (mostly) intended to pay off in the future with no impact on happiness now. Although there's no equivalent 'sharp' threshold for when you're forced to be a near-termist, my read is if your discount rate is ≥4% it starts to become really hard to justify any long-term philanthropy – any intervention which only pays off after 100 years is basically pointless in this scenario.
I have also highlighted my best guess for what the actual growth in happiness and discount rate should be[3] (in red). You can see that it straddles the line of ‘definitely be a long-termist’ and ‘depends on the quality of intervention’ very neatly. I suspect this is why debates about long and short-termism can be a little acrimonious; people think they are arguing about the quality of longtermist interventions, but they are actually swapping intuitions about whether the discount rate should be fractionally above 1.5% or fractionally below 1.5%, so nothing gets resolved.
The numbers themselves aren’t as important as the general shape of the output table, but just by way of a simple numerical demonstration; imagine the world currently generates about 6.2 gigaQALYs per year. You can choose to spend your philanthropic dollars on a donation to AMF which (very roughly) might give 0.01 QALY per dollar donated. Alternatively, you could choose to spend your philanthropic dollars on an AI alignment foundation, which has a 0.1% chance of being fundamental in some sense to preventing an extinction-level event from occurring in 80 years given an operating budget of $7.5m / year [4]. Which is the better option? The answer is that it is impossible to say without knowing the discount rate; in scenarios where the growth in happiness is greater than the discount rate, the AI foundation is infinitely better. In scenarios where the delta between growth in happiness and discount rate is less than 4% the AI foundation is still better, but the decision is becoming increasingly close. In scenarios where the delta is greater than 4%, the AMF is better.
My core conclusion is this; if you believe the discount rate is likely less than or equal to the rate of growth in happiness over time, you should be a long-termist. If you believe anything else then the terms 'long-termist' and 'near-termist' are basically meaningless; there is a specific rate at which you should be prepared to trade off QALYs now against QALYs in the future, and this tradeoff doesn't inherently favour long-term interventions; it depends on the specifics of the intervention and your own views about the discount rate.
- ^
Actually it is a little more involved than this – I’m simplifying for brevity’s sake. My actual understanding of the argument is that the future might matter more than the past because of the interaction between three mechanisms:
1) More people will be born, and these people will have their own stream of QALYs we can add to the total
2) Each person who is born will likely live longer in the future than they do now, so at the margin they have some QALYs that people born now do not
3) The moment-by-moment happiness of each individual might be higher in the future, for example because they worry less about disease and famine.
This doesn't really change anything I wrote above, but it does affect how confident we can be that we've nailed the rate of growth of happiness when we move ahead of simple demographic projections - these three elements will interact with each other in complex ways.
- ^
'Front-loading' is a feature of almost all possible models of discount rates, but in my experience exponential models are not especially front-loaded compared to other plausible specifications. The most common alternative specification to an exponential model is a hyperbolic model though, and that is a famously back-loaded approach. Note also that we don't have to have a fancy mathematical name for the shape of our discount rate - Will MacAskill has written that his discount rate for EA looks like "30% for the next couple of years ... tailing down to something close to 0% (and maybe even going negative for a while) after 5 or 6 years". This is a perfectly sensible specification of a discount rate, it just doesn't have a mathematical name (it looks a bit hyperbolic-y if you squint).
- ^
Very roughly, world population growth has been about 2% / year historically and tending downwards to about 1% / year in economically developed countries (i.e. what we hope the future will look like).
Life expectancy has been increasing at about 0.5% / year. However, I think this is slightly misleading because these hugely impressive gains mostly come from averting infant mortality. Averting infant mortality is extremely important but a ‘finite’ source of life expectancy improvement when it comes to very long-term scenario planning because eventually every country will have infant mortality rates near zero. In the UK life expectancy increase is more like 0.1% / year, which is probably a more credible long-term assumption.
Moment-by-moment happiness actually seems to be decreasing in economically developed countries, but maybe we think we are living in a particularly dismal period and in fact this trend might reverse in the future which would give a rate of about 0.25% / year.
All this by way of saying that based on current trends we’d expect the total happiness of the world to increase by no more than 3% / year, and probably a bit below 2% / year as countries move through demographic transition. This would look like the below:
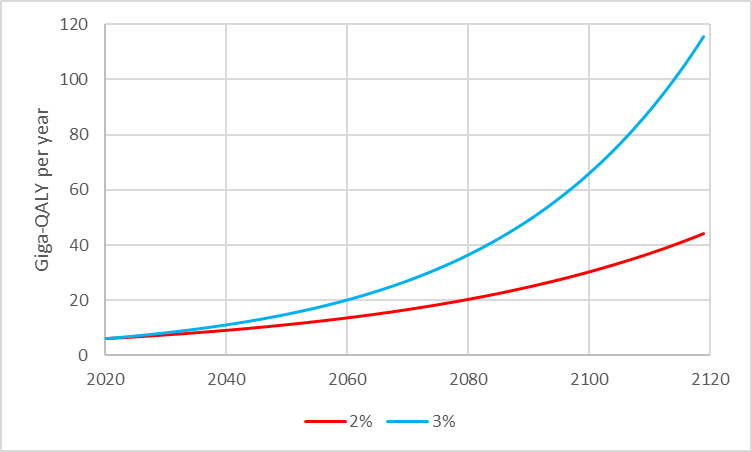
Discount rate is just the discount rate used by the UK government, less pure time preference.
- ^
Numbers picked because they are sort of plausible (I can defend them in the comments if requested), but mostly because they give a nice neat answer at the end of the calculation!

ADDENDUM: There is an excellent post here about why the discount rate is probably not zero based on an analysis of existential risk rates. However, I think the post assumes a lot of background familiarity with the theory of discount rates, and doesn’t – for example – explicitly identify that existential risk is probably not the biggest reason to discount the future (even absent time-preference). Would an effortpost which is a deep dive into discount rates as understood by economists be helpful?
Other views on decision theory and credences matter, too, like how you deal with cluelessness and what you're clueless about, whether you maximize expected value at all, whether you think you should do things that have only a 1 in a million chance of having the intended impact, the shape of your utility function, if any (both bounded and unbounded ones have serious problems).
I should make a post on cluelessness, but over the very long term future like thousands of years, longtermism suffers less than you think naively on cluelessness considerations.
Can you say a bit more about how each of those considerations affect whether one should be longtermist or short-termist?
A keyword to search for here might be "Patient Philanthropy", and in particular the work of Phil Trammel on this topic (e.g., 1, 2)
What if you did hyperbolic discounting rather than exponential discounting? What would change in this analysis?
Hyperbolic discounting is a 'time inconsistent' form of discounting where delays early on are penalised more than delays later on. This results in a 'fat tail' where it takes a long time for a hyperbolic function to get near zero. Over a long enough time period, an exponential function (for example growth in happiness driven by population growth) will always be more extreme than a hyperbolic function (for example discount rate in this scenario).
So actually the title should perhaps be reworded; the shape of the discount function matters just as much (if not more so than) the parameterisation of that function. A hyperbolic discount function will always result in longtermism dominating neartermism.
Having said that, I don't think anyone believes hyperbolic discount rates are anything other than a function of time preference, and the consensus amongst EAs seems to be that time preference should be factored out of philanthropic analysis.
Admittedly, this is a bit of a contrarian take on discount functions, but hyperbolic discounting is more rational than economists or EAs think once we introduce uncertainty. I'll provide links here for my contrarian take:
https://www.lesswrong.com/posts/tH8bBKCvfdjBKMDqt/link-hyperbolic-discounting-is-rational
http://physicsoffinance.blogspot.com/2011/07/discountingdetails.html?m=1