Comments
Google Doc | Author: Mati Roy | Created: 2020-11-28 | Published: 2020-12-08 | Updated: 2020-12-08 | Version: 2 | Epistemic status: 50% this is roughly right | Acknowledgement for feedback: Carl Shulman, Aahan Rashid, Kirsten Horton
Money lotteries, ie. a lottery where you gamble money, are useful when you’ve identified donation/purchase opportunities that have increasing marginal returns beyond your budget.
Time lotteries, ie. a lottery where multiple parts of your moral parliament gamble access to your mind, are useful when time has increasing marginal returns beyond one of your value’s budget at a sufficiently low premium cost for the other values. I think this is likely the case for people that are <1-20% altruistic.
We can model the problem as having a fixed hour-budget to be used for fulfilling a certain value, with some of the hours being used for personal research and others being used to earn money to donate. The function would be:
Here I’m using “time” as a unit for “capacity to do work”, which also includes things like mental energy.
The research and where you give the money can be very meta — for example, you can research whom you should give money to research where to give money.
This is new terminology I’m using.
By “unified self”, I mean an agent with one overarching morality — for the purpose of this text, a utility function.
By “fragmented self”, I mean an agent with many subagents taking decisions through a mechanism such as a moral parliament.
If you’re a unified self (ex.: a pure positive hedonistic utilitarian), then you will spend all your time fulfilling your morality. You can use lotteries if you can’t otherwise gather enough money, includying:
If you’re a fragmented self, then you can also use lotteries to bet money. But on top of it, you can also use time lotteries, ie. a lottery where multiple parts of your moral parliament gamble access to your mind.
For example, it seems to me like altruistic values benefit from a large amount of research and reflection. So if only 1% of your self is altruistic, then I would argue it would be better for your altruistic values to have a 20% chance of using 5% of your (life) time rather than a 100% chance of using 1% of your (life) time. I think this remains true even after adding a premium to compensate your non-altruistic values.
Time lotteries can be difficult as they require the ability to make pre-commitments. If you use a quantum lottery, it’s easy for different altruistic agents to cooperate as they know that if they defect in their branch*, it likely means the other versions will also defect. However, an egoistic agent might not care if the other versions don’t respect their commitment as it wouldn’t impact the egoistic agent’s values.
*Note: Even if you reject the many-world interpretation of quantum mechanics, and instead think the wave function collapses randomly, if you think the world is spatially infinite (with random initial conditions), you can still know there will be other versions of you where the wave function collapsed elsewhere, and so it’s still in the interest of your altruistic values to cooperate.
In terms of utilitarian values, I think time has increasing marginal return for a long time before starting decreasing — possibly a couple full-time years (related: Why Charities Usually Don't Differ Astronomically in Expected Cost-Effectiveness). So if you’re <1-20% altruistic, I think it makes sense for your different value systems to participate in a time lottery (although maybe you want to use some of your budget to verify this). If you’re 30-90% altruistic, I think you will have hit diminishing marginal returns for utilitarian values, but even if not, I think the premium charged by your non-altruistic values to enter a time lottery would likely become too high.
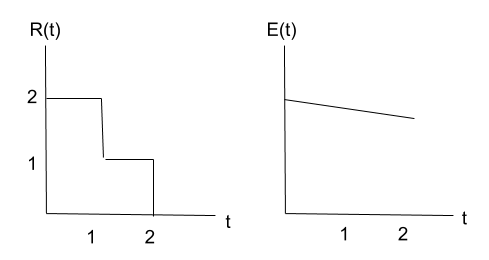
Note: In the model I use, even if both R(t) and E(t) have diminishing marginal returns, it can still be that ∫R(t)⋅dt * ∫E(t)⋅dt has increasing marginal return.
For example, with the following functions (see image below), it’s almost 50% better to have 4 units of time with 50% probability than 2 units of time with 100% probability.
CEA’s donor lotteries can be used for that, but really you just need to generate a random number yourself, along with having a commitment mechanism. Although, maybe having the lottery being public serves as a commitment mechanism.
As for using money, I think it generally has diminishing marginal returns. One potential notable exception is for biostasis (see: Buying micro-biostasis). To the extent there are other exceptions, then money lotteries are useful. (Do you have other notable examples?)
At the group level, reducing the variance of resources dedicated to a value is good if the resources have diminishing marginal returns past one individual worth of resources, which seems often the case.
Two ways to reduce the variance:
