___________________________________________________
tldr;
- Expected value theory misrepresents ruin games and obscures the dynamics of repetitions in a multiplicative environment.
- The ergodicity framework provides a better perspective on such problems as it takes these dynamics into account.
- Incorporating the ergodicity framework into decision-making can help prevent the EA movement from inadvertently increasing existential risks by rejecting high expected value but multiplicatively risky interventions that could lead to catastrophic outcomes.
___________________________________________________
Effective Altruism (EA) has embraced longtermism as one of its guiding principles. In What we owe the future, MacAskill lays out the foundational principles of longtermism, urging us to expand our ethical considerations to include the well-being and prospects of future generations.
Thinking in Bets
In order to consider the changes one could make in the world, MacAskill argues one should be “Thinking in Bets”. To do so, expected value (EV) theory is employed on the account that it is the most widely accepted method. In the book, he describes the phenomenon with an example of his poker-playing friends:
“Liv and Igor are at a pub, and Liv bets Igor that he can’t flip and catch six coasters at once with one hand. If he succeeds, she’ll give him £3; if he fails, he has to give her £1. Suppose Igor thinks there’s a fifty-fifty chance that he’ll succeed. If so, then it’s worth it for him to take the bet: the upside is a 50 percent chance of £3, worth £1.50; the downside is a 50 percent chance of losing £1, worth negative £0.50. Igor makes an expected £1 by taking the bet—£1.50 minus £0.50. If his beliefs about his own chances of success are accurate, then if he were to take this bet over and over again, on average he’d make £1 each time.”
More theoretically, he breaks expected value theory down into three components:
- Thinking in probabilities
- Assigning values to outcomes (What economists call Utility Theory)
- Taking a decision based on the expected value
This logic served EA well during the early neartermist days of the movement, where it was used to answer questions like: “Should the marginal dollar be used to buy bednets against malaria or deworming pills to improve school attendance?”.
The Train to Crazy Town
Yet problems arise when such reasoning is followed into more extreme territory. For example, based on its consequentialist nature, EA-logic prescribes pulling the handle in the Trolley Problem[1]. However, many Effective Altruists (EAs) hesitate to follow this reasoning all the way to its logical conclusion. Consider for instance whether you are willing to take the following gamble: you're offered to press a button with a 51% chance of doubling the world's happiness but a 49% chance of ending it.
This problem, also known as Thomas Hurka's St Petersburg Paradox, highlights the following dilemma: Maximizing expected utility suggests you should press it, as it promises a net positive outcome. However, the issue arises when pressing the button multiple times. Despite each press theoretically maximizing utility, pressing the button over and over again will inevitably lead to destruction. Which highlights the conflict between utility maximization and the catastrophic risk of repeated gambles.[2] In simpler terms, the impact of repeated bets is concealed behind the EV.
In EA-circles, following the theory to its logical extremes has become known as catching “The train to crazy town”[[3],[4]]. The core issue with this approach is that, while most people want to get off the train before crazy town, the consequentialist expected value framework does not allow one to get off. Or as Peter McLaughlin puts it: “The train might be an express service: once the doors close behind you, you can’t get off until the end of the line”[5]. This critique has been influential as it directly attacks the ethical foundation of the Effective Altruism movement. One could argue; why believe in a movement that is not even willing to follow its own principles? Since this critique has received considerable - and better - treatment both from inside[3,[6]] and outside[[7],[8],[9]] the EA community, I will only link to those discussions here.
The train to crazy town: a ride without stops
The fact that EAs differ in their willingness to follow expected value theory to its extremes has put the EA community at a crossroads[10]. On the one hand, the fanaticism camp preaches consistency within the consequentialist-expected value theory framework. They are, therefore, willing to bite all bullets on the way to crazy town. Philosophical leaders like Toby Ord and William MacAskill are part of this camp. When pressed on this issue by Tyler Cowen, MacAskill urges us to try harder with our moral reasoning:
Cowen: “Your response sounds very ad hoc to me. Why not just say, in matters of the very large, utilitarian kinds of moral reasoning just don’t apply. They’re always embedded in some degree of partiality.”
MacAskill: “I think we should be more ambitious than that with our moral reasoning.” [11]
On the other hand, the pluralist view focuses on integrating multiple moral values and considerations into its decision-making and prioritization framework. In this manner, the pluralist view urges us to not solely rely on utilitarian calculations of maximizing happiness or reducing suffering. This allows one to not follow utilitarianism to its logical extremes but, by doing so, undermines the moral philosophy on which it is built. To stick with the analogy, this allows one to get off the train to crazy town at the expense of derailing the EA train.
But what if there is a way to - at least partially - reconcile these two perspectives? A way to follow consequentialist reasoning without arriving in crazy town? A way to get off the train without derailing it?
The answer lies in a subtle assumption Daniel Bernoulli[12] made when he was the first to write down how to Think in Bets in 1738. To understand how this works, we must take a look at Ole Peter’s work. Ole Peters[13] is a physicist at the London Mathematical Laboratory who started the field of Ergodicity Economics.
Ergodicity view: Additive versus multiplicative games
Ole Peters points out that many economic models assume our world is ergodic—that is, they assume looking at an average outcome over time or across many people can tell us what to expect from an individual. If a process is ergodic, the average over time will be the same as the ensemble average, an average over multiple systems. A simple example in which this is the case is the following: When one person plays head-or-tails 1000 times, and when 1000 people play once, both situations are expected to hit heads 500 times. Just like the expected value theory would suggest. But real life, especially long-term population ethics, often doesn't work that way.
For example, consider playing a game where you flip a coin, and if it's heads, you increase your wealth by 50%, but if it's tails, you lose 40%. Mathematically, the average outcome looks positive. But, if you play this game repeatedly, because of the multiplicative nature of wealth (losing 40% can't just be "averaged out" by gaining 50% later), you're likely to end up with less money over time. This game is non-ergodic - the long-term outcome for an individual doesn't match the seemingly positive average outcome.
The attentive reader will have realised the similarities between the aforementioned St Petersburg paradox and this gambling problem. In both cases, one following the expected value theory would take the bet. Yet, playing repeatedly results in losing money over time[14] or the destruction of the world[15]. It is like someone playing Russian roulette on repeat. There are two factors at play here that create this dynamic. First, due to its multiplicative nature, all the wealth of a person is at stake at once instead of only a part of it, as in the example of MacAskill’s poker friends. The second dynamic is repetitiveness. It is correct that, a single flip of the coin does yield a positive expected value. Yet, a consequentialist caring about one’s wealth at the end of the 1000 periods would decide not to play.
The dynamics at play in Ergodicity Economics seem counterintuitive at first, especially for economists and EAs who have become hardwired to think in terms of Utility Theory and Expected Value Theory, respectively. To better understand the concept of non-ergodic processes, I link here an explanation video by Ole Peters[16], a blog article in which one can simulate the gamble above[17], and the seminal paper by Peters in Nature[18].
It is important to note that Thomas Aitken’s[19] EA-Forum post has already demonstrated how ergodicity economics can serve as an analytical lens to critique EA. My contribution is in integrating this with consequentialist logic, which facilitates a way of getting off the proverbial 'train to crazy town'.
Ruin Problems
Next, I will show how, in the presence of the possibility of ruin, Expected Utility Theory breaks down in a longtermist framework[20]. To do so, we first take a philosophical perspective before turning to a more economic approach.
EAs who are willing to bite the bullet on Thomas Hurka’s St. Petersburg Paradox employ the wrong mental model. They assume to be taking a gamble on a world state of doubling the world utility versus destroying one world utility. However, due to the potential loss of all of future humanity, the downside in this gamble should be characterised as negative infinity.
Since we are manoeuvring in the philosophical world, let’s assume a zero social discount rate, as Parfit and Cowen argued in 1992[[21]]. In such a world, all potential future people should be fully incorporated into our future utility function (1).

Let U(t) represent the aggregate utility of all individuals alive at time (t)
. Assume that the total world utility,
W, is the sum of all future utilities discounted by the probability of human survival up to that point. If
p(t) is the probability of human survival until time (t)
Here, p(t) decreases over time due to the presence of extinction risk in all time periods. For simplicity, let’s assume a constant risk of extinction per unit of time
, labda, so p(t)= e^(-labda *t).
Let’s now assume that an extinction event occurs at a time
T, this will truncate the integral and lead to (2).
Lastly, let’s now look at the potential future utility wasted (3).
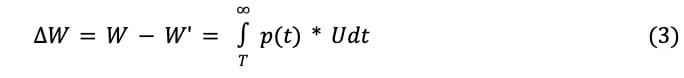
If the utility function U(t) does not diminish to zero—people keep living happy lives on earth—at a rate faster than the rate at which the survival probability function decreases, then the integral that defines the change in world utility can diverge, implying an infinite loss. In short, expected values don’t fare well in the presence of infinities.
Thus, assuming a zero discount rate leads to an infinite loss in utility in the aforementioned paradox. Cowen and Parfit agree that utilitarian logic breaks down when confronted with infinites[22]. In theory, this justifies a full allocation of EA resources to existential risk (X-risk) reduction.
Of course there are many practical objections to the argument made above. The goal here is to expose the flaw in EV-theory, not to come up with an accurate EV estimate of X-risk. Additionally, there has been a lot of impressive work trying to quantify the expected value of X-risk under more practical and economic assumptions[[23],[24]].
Ergodicity perspective on ruin problems
Having shown that Expected Utility Theory breaks down when confronted with infinity, I will argue that the ergodicity framework provides the correct intuitive perspective to this problem. Let’s modify the St. Petersburg Paradox to the one that Cowen puts in front of MacAskill: “you're offered to press a button with a 90% chance of doubling the world's happiness but a 10% chance of ending it. But, we play 200 times”. Below one can see the amount of worlds still existing after the amount of rounds played, simulated for 500 worlds.
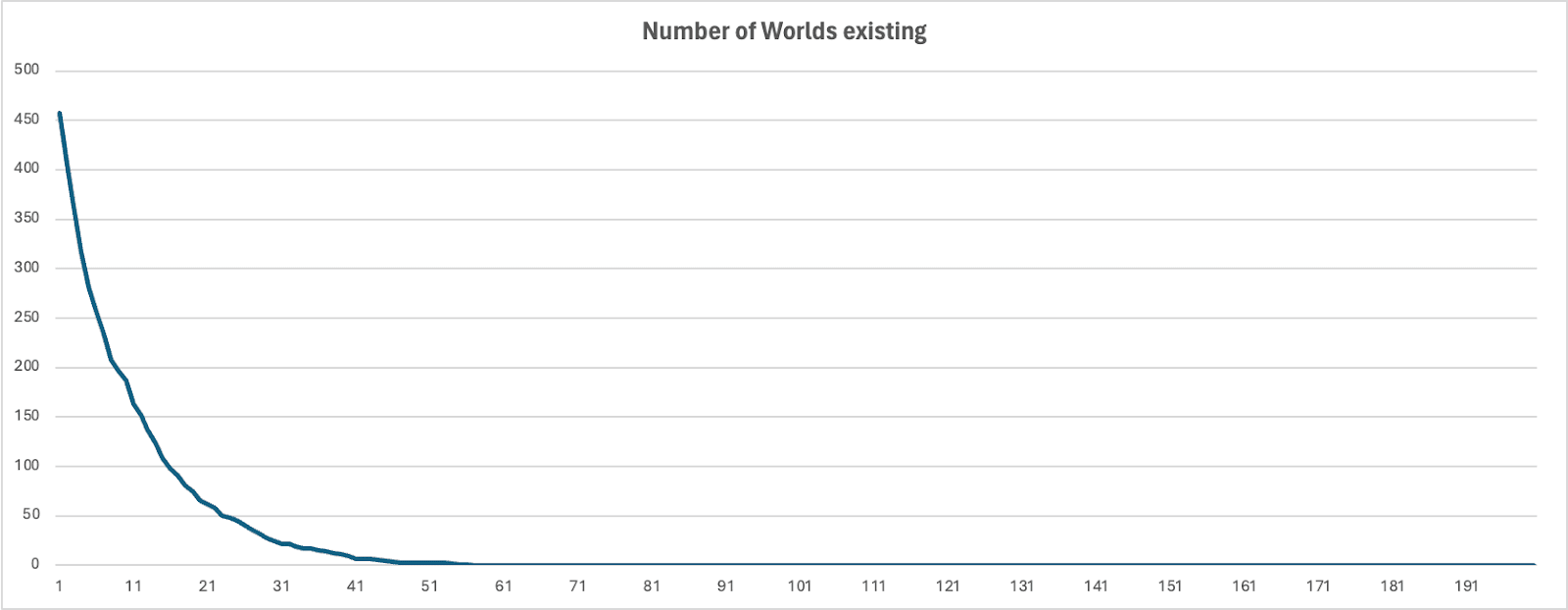
This figure shows the number of worlds that still exist in a total of 500 simulations of the Tyler Cowen St. Petersburg Paradox. The last world dies after 59 rounds in this simulation.
MacAskill struggles with the paradox and, when put on the spot during the interview, jumps to moral pluralism as a solution. Yet, it is possible to answer these questions from within a consequentialist framework when taking Ergodicity seriously.
It is true that the total happiness in round 59, the last round in which a world exists, is times as high as in the initial state, which in a consequentialist framework, would outweigh the loss of 499 worlds. However, every consequentialist asked to evaluate whether to take the gamble for 200 consecutive rounds would not take the bet. These dynamics are caused by certain absorption barriers from which one cannot recover[25]. They are characterized by the system's eventual transition into one of these absorbing states, regardless of the initial state, thus capturing long-term behaviours and outcomes. Ruin games are therefore a special case of ergodicity. Not only do ruin games have a different time average than the ensemble average, but their end state also creates a point of no return.
My argument to this point can be summarised as; Expected value theory misrepresents ruin games and obscures the dynamics of repetitions in a multiplicative environment. Or, as Nassim Taleb’s[26] states it: “[S]equence matters and ruin problems don’t allow for cost-benefit analysis.”.
Non-ergodicity for EA: a framework
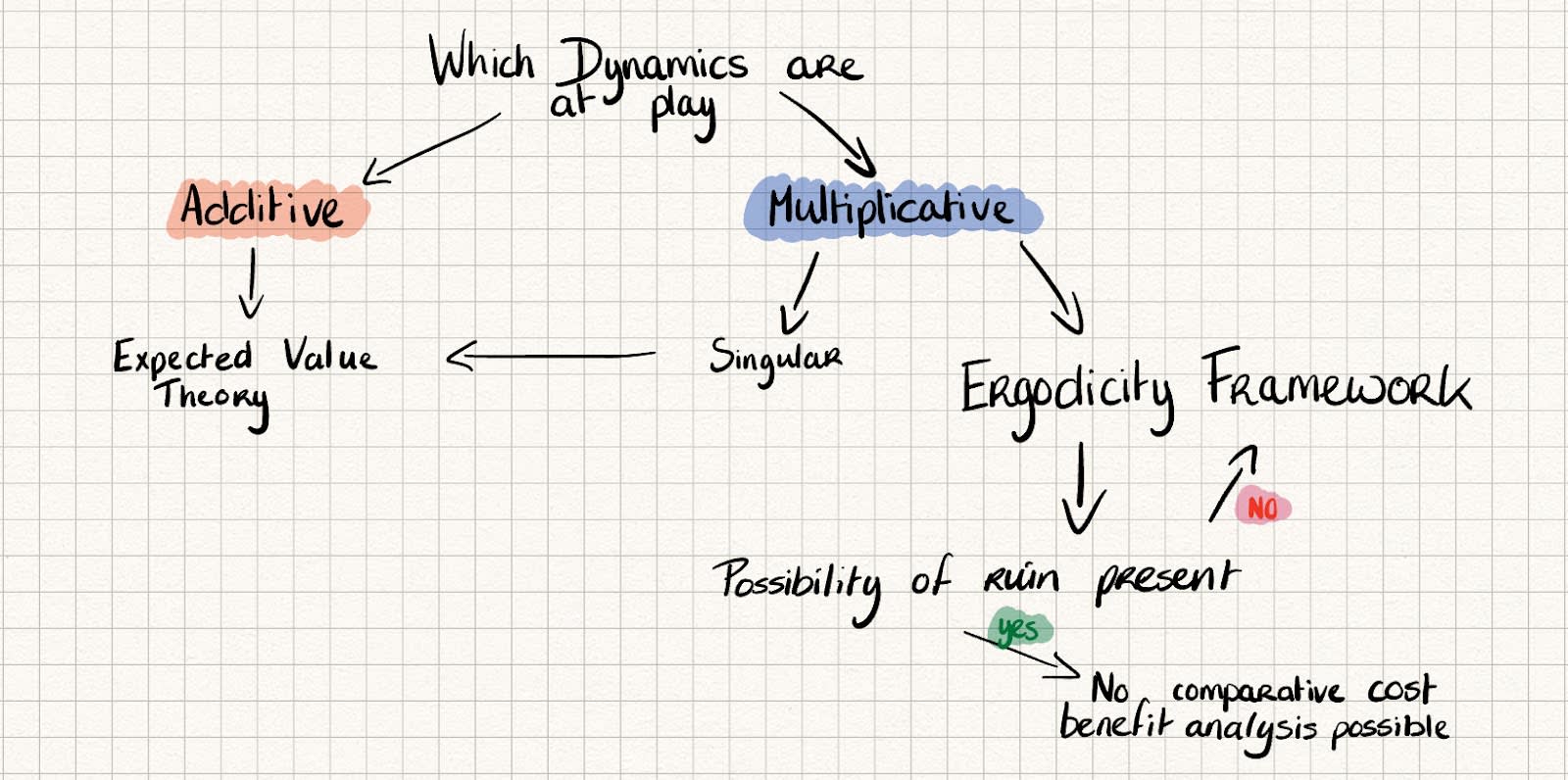
So, instead of a priori assuming that one can follow the expected value theory. One should first ask the question: What game are we playing? Or, which dynamics are in play?
MacAskill can be forgiven for not being aware of the implicit ergodicity assumption in expected value theory when writing the book. The first paper by Peters and Nobel laureate Gell-Man was only written in 2016[27], and Ergodicity Economics still forms a niche within the discourse. Yet, ergodicity should be intuitively appealing to EA as it is a mathematical concept.
In a sense, it is not consequentialist reasoning that breaks down in this particular extreme. What breaks down is the implicit assumption of ergodicity within expected value theory. In other words, the core issue is its failure to consider time, which is exposed in the limit. Therefore, it is not consequentialism that breaks down in the extreme, it is the Utility Framework.
From a purely philosophical perspective, the singular instance remains a challenge for utilitarianism. Yet, the ergodicity perspective provides a clear stop on our way to crazy town in the case of repeated multiplicative dynamics. The figure below provides a flowchart of when expected value theory suffices and when an ergodicity framework is necessary.
Figure: A new consequentialist framework for how to ‘Think in Bets’ depending on the dynamics at play.
Some implications
Taking ergodicity seriously can strengthen the EA longtermist movement both from a theoretical and a practical perspective. First, it allows for a resolution of the St Petersburg Paradox and similar thought experiments. It does so by incorporating the importance of compounding sequence effects and ruin states in the consequentialist framework. For EAs, this allows for a stop on the train to crazy town within the consequentialist framework, at least in the case of St. Petersburg-like paradoxes.
As a consequence, in a repeating multiplicative environment, the ergodicity framework allows one to consider sequence effects. By doing so, it allows one to reject risky ‘positive expected utility bets’ from within the consequentialist framework. This holds as long as these bets are expected to be multiplicative. To illustrate this point, let’s look at the example Hayley Clatterbuck gave during the EAG Bay Area conference last month[28].
The highest EV intervention given here is ‘virus hunting’, which involves having labs research and create viruses that could produce the next extinction-level pandemic. The EV of this intervention could be high if we find these viruses ahead of time and are able to develop vaccines upfront. Yet, when the virus breaks out of the lab—a backfire event— the outcomes would be devastating. Let’s now assume that EA grantmakers double down on this X-risk intervention over the upcoming years, because it has the highest EV. Since this is a nascent field, the effect that the marginal lab will have is proportional to the current level of biosecurity risk. In other words, since the field has not hit its limits to growth, multiplicative dynamics are in play. In this scenario, the average over time will be different than its ensemble average, so non-ergodicity is in play. Additionally, depending on the values given to the different probabilities[29], X-risk might increase. This can be true even for high EV scores. Thus, a grantmaker who repeatedly makes decisions on interventions to reduce X-risk based on EV scores could inadvertently increase X-risk. All while he is trying to save the world.
Of course, the prior argument requires many assumptions. Given this, my point is not to argue that all the assumptions above are true. It is to show that the ergodicity framework elicits the assumptions obscured in the EV framework. Additionally, it allows one to reject discounting and risk aversion, core longtermist and consequentialist positions, and still decide not to take ‘risky positive expected utility bets’.
Let’s also be clear about what I do not attempt with this post. This post does not provide an answer to the repugnant conclusion or other thought experiments on the train to crazy town. Thus, it is not an all-encompassing solution to the controversial consequences of consequentialism. It is only a first attempt at being more ambitious with our moral reasoning, as MacAskill called for.
- ^
KILLING, LETTING DIE, AND THE TROLLEY PROBLEM The trolley problem is a thought experiment where you must decide between taking action to divert a runaway trolley onto a track where it will kill one person, or doing nothing and allowing it to continue on its current path, killing five.
- ^
Value and Population Size* - Thomas Hurka Thomas Hurka (1983) Value and Population size.
- ^
- ^
- ^
- ^
- ^
- ^
- ^
- ^
Integrating utilitarian calculations into moral theory leads to their dominance, which results in the extreme outcomes described above. Although some may accept controversial consequences like the repugnant conclusion or the experience machine, many will encounter an unacceptable scenario that challenges their adherence to utilitarianism. Rejecting such scenarios requires abandoning the principle that the magnitude of outcomes always matters, highlighting a fundamental inconsistency within utilitarian logic.
- ^
- ^
- ^
- ^
Because of the multiplicative dynamics in which on average ones wealth is reduced, in the limit one’s wealth would converge to 0.
- ^
The dynamics at play in the Thomas Hurda’s St. petersburg Paradox can be characterised as a ruin game.
- ^
- ^
- ^
- ^
- ^
This does not apply to neartermists issues because in this case the cost of ruin can be accounted for. Ruin, one person dying, can be accounted for through the cost per quality adjusted life year (QALY). Yet there is no equivalent metric for longtermism, because humanity is still singular.
- ^
- ^
- ^
- ^
- ^
In probability theory, such states are called absorbing Markov Chains. Interesting article on how Markov Chain modeling can improve X-risk calculations. Existential Risk Modelling with Continuous-Time Markov Chains — EA Forum
- ^
- ^
- ^
- ^
I deliberately do not assign probabilities in this case, as it would distract from the argument I am trying to make. In an upcoming blog, I will dive into the numbers and show the effects of different parametrisations on X-risk models.




Like most defenses of ergodicity economics that I have seen, this is just an argument against risk neutral utility.
Edit: I never defined risk neutrality. Expected utility theory says that people maximize the expectation of their utility function, E[U(c)]. Risk neutrality means that U(c) is linear, so that maximizing expected utility is the exact same thing as maximizing expected value of the outcome c. That is, E[U(c)]=U(E[c]). However, this is not true in general. If U(c) is concave, meaning that it satisfies diminishing marginal utility, then E[U(c)]<U(E[c]) - in other words, the expected utility of a bet is less than the utility of its expected value as a sure thing. This is known as risk aversion.
No. A risk neutral agent would press the button because they are maximizing expected happiness. A risk averse agent will get less utility from the doubled happiness than the utility they would lose from losing all of the existing happiness. For example, if your utility function is U(c)=√c and current happiness is 1, then the expected utility of this bet is E[U(c)]=0.51∗√2+0.49∗√0≈0.72. Whereas the current utility is √1=1 which is superior to the bet.
When you are risk averse, your current level of happiness/income determines whether a bet is optimal. This is a simple and natural way to incorporate the sequence-dependence that you emphasize. After winning a few bets, your income/happiness have grown so much that the value of marginal income/happiness is much lower than what you already have, so losing it is not worthwhile. Expected utility theory is totally compatible with this; no ergodicity economics needed to resolve this puzzle.
Now, risk aversion is unappealing to some utilitarians because it implies that there is diminishing value to saving lives, which is its own bullet to bite. But any framework that takes the current state of the world into account when deciding whether a bet is worthwhile has to bite that bullet, so it's not like ergodicity economics is an improvement in that regard.
Thanks for reading and the insightful reply!
I agree with one subtle difference: the ergodicity framework allows one to decide when to apply risk neutrality and when to apply risk aversion.
Following, Cowen and Parfit, let’s make the normative claim one wants to be risk neutral because one should not assume a diminishing value to saving lives. The EE framework allows one to divert from this view when multiplicative and repetitive dynamics are in play (i.e. wealth dynamic bets and TH St. Petersburg Paradox). Thus, not being risk-averse based on some pre-defined utility function, but because the actual long-term outcome is worse (going bankrupt and destroying the world). An actor can therefore decide to be risk neutral in scenario A (i.e. neartermist questions) and risk averse in scenario B (i.e. longtermist questions).
PS: you're completely right on the 'risk neutral agent' part my wording was ambigious.
If you are truly risk neutral, ruin games are good. The long term outcome is not worse, because the 99% of times when the world is destroyed are outweighed by the fact that it's so much better 1% of the time. If you believe in risk neutrality as a normative stance, then you should be okay with that.
Put another way; if someone offers you a 99% bet for 1000x your money with a 1% chance to lose it all, you might want to take it once or twice. You don't have to choose between "never take it" and "take it forever". But if you find the idea of sequence dependence to be desirable in this situation, then you shouldn't be risk neutral.
Deciding to apply risk aversion in some cases and risk neutrality in others is not special to ergodicity either. If you have a risk averse utility function the curvature increases with the level of value. I claim that for "small" values of lives at stake, my utility function is only slightly curved, so it's approximately linear and risk neutrality describes my optimal choice better. However, for "large" values, the curvature dominates and risk neutrality fails.
The long-term outcome in this game is only the correct thing to optimize for under specific circumstances (namely, the circumstances where you have a logarithmic utility function). Paul Samuelson discussed this in Why we should not make mean log of wealth big though years to act are long. For a more modern explanation, see Kelly is (just) about logarithmic utility on LessWrong.
Are you saying that it immediately produces solutions? Or that it hasn't produced solutions yet, but it might with more research? For example, what does an ergodicity framework say is the correct amount to bet in the St. Petersburg game? Or the correct decision in Cowen's game where you have a 90% chance to double the world's happiness and a 10% chance to end it?
(I should say that my questions are motivated by the fact that I'm pretty skeptical of ergodicity as a useful framework, but I don't understand it very well so I could be missing something. I skimmed the Peters & Gell-Mann paper and I see it makes some relevant claims like "expectation values are only meaningful in the presence of [...] systems with ergodic properties" and "Maximizing expectation values of observables that do not have the ergodic property [...] cannot be considered rational" but I don't see where it justifies them, and they're both false as far as I can tell.)
I came up with a few problems that pose challenges for ergodicity economics (EE).
First I need to explicitly define what we're talking about. I will take the definition of the ergodic property as Peters defines it:
More precisely, it must satisfy
limT→∞1TT∫0f(W(t))dt=∫f(W)P(W)dW
where W(t) is wealth at time t, f(W) is a transformation function that produces the "observable", and the second integral is taking the expected value of wealth across all bet outcomes at a single point in time. (Peters specifically talked about wealth, but W(t) could be a function describing anything we care about.)
According to EE, a rational agent ought to maximize the expected value of some observable f(W) such that that observable satisfies the ergodic property.
Problem of choosing a transformation function
According to EE, making decisions in a non-ergodic system requires applying a transformation function to make it ergodic. For example, if given a series of bets with multiplicative payout, those bets are non-ergodic, but you can transform them with f(W(t),W(t+1))=log(W(t+1)W(t))=log(W(t+1))−log(W(t)), and the output of f now satisfies the ergodic property.
(Peters seems confused here because in The ergodicity problem in economics he defines the transformation function f as a single-variable function, but in Evaluating gambles using dynamics, he uses a two-dimensional function of wealth at two adjacent time steps. I will continue to follow his second construction where f is a function of two variables, but it appears his definition of ergodicity is under-specified or possibly contradictory.)
The problem: There are infinitely many transformation functions that satisfy the ergodic property.
The function "f(x) = 0 for all x" is ergodic: its EV is constant wrt time (because the EV is 0), and the finite-time average converges to the EV (b/c the finite-time average is 0). There is nothing in EE that says f(x) = 0 is not a good function to optimize over, and EE has no way of saying that (eg) maximizing geometric growth rate is better than maximizing f(x) = 0.
Obviously there are infinitely many constant functions with the ergodic property. You can also always construct an ergodic piecewise function for any given bet ("if the bet outcome is X, the payoff is A; if the bet outcome is Y, the payoff is B; ...")
Peters does specifically claim that
These assumptions are not directly entailed by the foundations of EE, but I will take them as given. They're certainly more reasonable than f(x) = 0.
Problem of incomparable bets
Consider two bets:
EE cannot say which of these bets is better. It doesn't evaluate them using the same units: Bet A is evaluated in dollars, Bet B is evaluated in growth rate. I claim Bet B is clearly better.
There is no transformation function that satisfies Peters' requirement of maximizing geometric growth rate for multiplicative bets (Bet B) while also being ergodic for additive bets (bet A). Maximizing growth rate specifically requires using the exact function f(W(t),W(t+1))=log(W(t+1)W(t)), which does not satisfy ergodicity for additive bets (expected value is not constant wrt t).
In fact, multiplicative bets cannot be compared to any other type of bet, because log(W(t+1)W(t)) is only ergodic when W(t) grows at a constant long-run exponential rate.
More generally, I believe any two bets are incomparable if they require different transformation functions to produce ergodicity, although I haven't proven this.
Problem of risk
This is relevant to Paul Samuelson's article that I linked earlier. EE presumes that all rational agents have identical appetite for risk. For example, in a multiplicative bet, EE says all agents must bet to maximize expected log wealth, regardless of their personal risk tolerance. This defies common sense—surely some people should take on more risk and others should take on less risk? Standard finance theory says that people should change their allocation to stocks vs. bonds based on their risk tolerance; EE says everyone in the world should have the same stock/bond allocation.
Problem of multiplicative-additive bets
Consider a bet:
More generally, consider the class of bets:
Call these multiplicative-additive bets.
EE does not allow for the existence of any non-constant evaluation function for multiplicative-additive bets. In other words, EE has no way to evaluate these bets.
Proof.
Consider bet A above. By the first clause of the ergodic property, the transformation must satisfy (for some wealth value x)
12f(x,2x)+12f(x,x−1)=k
for some constant k. This equation says f must have a constant expected value.
Now consider what happens at x = -1. There we have 12f(−1,−2)+12f(−1,−2)=k and therefore f(−1,−2)=k.
That is, f(-1, -2) must equal the expected value of f for any x.
we can generalize this to all multiplicative-additive bets to show that the transformation function must be a constant function.
Consider the class of all multiplicative-additive bets. The transformation function must satisfy
12f(x,ax)+12f(x,x−b)=kab
for some constants a, b which define the bet (in Bet A, a = 2 and b = 1). (Note: It is not required that a and be be positive.)
The transformation function f(x,y) must equal kab when x=b1−a. To see this, observe that ax=ab1−a and x−b=b1−a−b(1−a)1−a=ab1−a, so f(x,ax)=f(x,x−b)=f(b1−a,ab1−a).
For any pair a,b defining a particular additive-multiplicative bet, it must be the case that f(b1−a,ab1−a) is a constant (and, specifically, it equals the expected value of the transformation function with parameters a,b).
Next I will show that, for (almost) any x,y pair in f(x,y), there exists some pair a,b that forces f(x,y) to be a constant.
Solving for a,b in terms of x,y, we get a=yx,b=x−y. This is well-defined for all pairs of real numbers except where x=0. For any pair of values x≠0,y we care to choose, there is some bet parameterized by a=yx,b=x−y such that f(x,y) is a constant.
Therefore, if there is a function f(x,y) that is ergodic for all additive-multiplicative bets, then that function must be constant everywhere (except on the line x=0, i.e., where your starting wealth is 0, which isn't relevant to this model anyway). A constant-everywhere function says that every multiplicative-additive bet is equally good.
EDIT: I thought about this some more and I think there's a way to define a reasonable ergodic function over a subset of multiplicative-additive bets, namely where a > 1 and b > 0. Let
f(x,y)=log(y/x)if x<y f(x,y)=y−xif x>y
This gives k=12log(a)−12b which is the average value, and I think it's also the long-run expected value but I'm not sure about the math, this function is impossible to define using the single-variable definition of the ergodic property so I'm not sure what to do with that.
(Sorry this comment is kind of rambly)
I looked through the first two pages of Google Scholar for economics papers that cite Peters' work on ergodicity. There were a lot of citations but almost none of the papers were about economics. The top relevant(ish) papers on Google Scholar (excluding other papers by Peters himself) were:
which is true AFAICT(edit: actually I don't think this is true). This paper's author admits some confusion about what ergodicity economics prescribes and he interprets it as prescribing maximizing geometric growth rate, which wasn't my interpretation, and I think this version is in fact falsifiable, and indeed falsified—it implies investors should take much more risk than they actually do, and that all investors should have identical risk tolerance, which sounds pretty wrong to me. But I read the Peters & Gell-Mann article as saying not to maximize geometric growth rate, but to maximize a function of the observable that has the ergodic property (and geometric growth of wealth is one such function). I think that's actually a worse prescription because there are many functions that can generate an ergodic property so it's not a usable optimization criterion (although Peters claims it provides a unique criterion, I don't see how that's true?). Insofar as ergodicity economics recommends maximizing geometric growth rate, it's false because that's not a good criterion in all situations, as discussed by Samuelson linked in my previous comment (and for a longer, multi-syllabic treatment, see Risk and Uncertainty: A Fallacy of Large Numbers where Samuelson proves that the decision criterion "choose the option that maximizes the probability of coming out ahead in the long run" doesn't work because it's intransitive; and an even longer take from Merton & Samuelson in Fallacy of the log-normal approximation to optimal portfolio decision-making over many periods. Anyway that was a bit of a tangent but the Toda paper basically says nobody has explained how ergodicity economics can provide prescriptions in certain fairly simple and common situations even though it's been around for >10 years years.So basically, I found a few favorable articles but they were shallow, and all the other articles were critiques. Some of the critiques were harsh (calling ergodicity pseudoscience or confused) but AFAIK the harshness is justified. From what I can tell, ergodicity economics doesn't have anything to contribute.
You might be interested to know that I also wrote a paper with John Kay critiquing EE, which was published with Econ Journal Watch last year. 'What Work is Ergodicity Doing in Economics?' was an earlier and more general survey for a seminar, and as you note was quite wordy! The EJW paper is targeted at EE, more mathematical, generally tighter, and introduces a few new points. Peters and some other coauthors responded to it but didn't really address any of the substantive points, which I think is further evidence that the theory's just not very good.
Thanks for linking your paper! I'll check it out. It sounds pretty good from the abstract.
Your ability and patience to follow Peters' arguments is better than mine, but his insistence that the field of economics is broken because its standard Expected Utility Theory (axioms defined by von Neumann, who might just have thought about ergodicity a little...) neglected ergodic considerations reminds me of this XKCD. Economists don't actually expect rational decision makers to exhibit zero risk aversion and take the bet, and Peters' paper acknowledges the practical implementation of his ideas is the well-known Kelly criterion. And EA utilitarians are unusually fond of betting on stuff they believe is significantly +EV in prediction markets without giving away their entire bankroll each time (whether using the Kelly criterion or some other bet-sizing criteria), so they don't need a paradigm shift to agree that if asked to bet the future of the human race on 51/49% doubling/doom game, the winning move is not to play.
afaik the only EA to have got "on the train to crazytown" to the point where he told interviewers that he'd definitely pick the 51% chance of doubling world happiness at the 49% risk of ending the world is SBF, and that niche approach to risk toleration isn't unlinked to his rise and fall. (It's perhaps a mild indictment of EA philosophers' tolerance of "the train to crazytown" that he publicly advocated this as the EA perspective on utilitarianism without much pushback, but EA utilitarianism is more often criticised for having the exact opposite tendencies: longtermism being extremely risk averse. Not knowing what the distribution of future outcomes actually looks like is a much bigger problem than naive maximization)
Other commenters have made some solid points here about the problems with ergodicity economics (EE) in general. I've also addressed EE at length in a short paper published last year, so won't go over all that here. But there are three specific implications for the framework you've presented which, I think, need further thought.
Firstly, a lot of EE work misrepresents expected utility as something that can only be applied to static problems. But this isn't the case, and it has implications for your framework. You say that for situations with an additive dynamic, or which are singular, expected value theory is the way to go, whereas for multiplicative dynamics we should use EE. But any (finite) multiplicative dynamic can be turned into a one-off problem, if you assume (as EE does) that you don't mind the pathway you take to the end state. (For example: we can express Peters' coin toss as a repeated multiplicative dynamic, but we can also ask 'Do you want to take a bet where you have a 25% chance of shrinking your wealth by 64%, a 50% chance of shrinking it by 10%, and a 25% chance of increasing it by 125%?'.) So your framework doesn't actually specify how to approach these situations.
Secondly: ruin. You don't provide a very clear definition of what counts as a 'ruin' problem. For example, say I go to a casino. I believe that I have an edge which will, if I can exploit it all night, let me win quite a chunk of money, which I will donate to charity. However I only have so much cash on me and can't get more. If I'm unlucky early on then I lose all my cash and can't play any more. This is an absorbing state (for this specific problem) and so would, I think, count as a ruin problem. But it seems implausible that we can't subject it to the same kind of analysis that we would if the casino let me use my credit card to buy chips.
Treating ruin as a totally special case also risks proving too much. It would seem to imply that we should either drop everything and focus on, for example, a catastrophic astroid strike, or that we just don't have a framework for dealing with decisions in a world where there could, possibly, one day be a catastrophic asteroid strike. This doesn't seem very plausible or useful.
The third issue follows from the first two. There are clear issues with Expected Value Theory and with Expected Utility Theory more broadly. But there are also some clear justifications for their use. It's unclear to me what your justification for using EE is. Since EE is incompatible with expected utility theory in general, which includes expected value maximisation, it seems curious that both of these coexist in your framework for making ethical decisions.
I appreciate you want to avoid apparent paradoxes which result from applying expected value theory, but I think you still need some positive justification for using EE. Personally I don't think such a justification exists.
Thanks for the post, Arthur.
I think biting the bullet on St. Petersburg paradox has basically no practictal implications, as one will arguably never be presented with the opportunity of doubling the value of the future with 51 % chance and ending it with 49 %. In contrast, rejecting expected utility maximisation (as you suggest) requires rejecting at least one of the axioms of Von Neumann–Morgenstern rationality:
Do you think one can reasomably reject any of these?
Interesting framework to address some of the key problems for the consequentialist train of thought. Your framework sounds like a good way forward. Thanks for sharing!
One practical question I have revolves around uncertainty. We usually don't know the exact "rules" of the moral "betting games" we are playing. How do we distinguish a cumulative problem from a multiplicative one?
Also, similar problems exist in biology, and the results from there might have interesting implications for effective strategies in the face of multiplicative risks, especially ruin problems. In brief, when you model population dynamics, you can do it in a deterministic or stochastic* manner. The deterministic models are believed to be a mean of the stochastic ones, kinda like the expected value problem. But this only works if we have big populations. If the population is small, with random effects it is likely to die out. So, whether averaging works, depends on the population size, which is often given in numbers of individuals but is, in reality, much more complex than that and relates to internal diversity.
How does that connect with ergodicity and ruin problems? Consider it in the context of value lock-in (as in Willam MacAskill's "What Do We Owe the Future") and general homogenization of Earth's social (and environmental) systems. If we all make the same bets, even if they have the best, ergodicity-corrected expected values, once we lose, we lose it all (Willam MacAskill gives an interesting example of a worryingly uniform response to COVID-19, see "What Do We Owe the Future" Ch. 4). This is equivalent to a small population in the biological systems. A diverse response means that a ruin is not a total ruin. This is equivalent to large populations in biological systems. You can think about it as having multiple AGIs, instead of one "singularity", if this is your kind of thing. Either way, while social diversity by no means solves all the problems, and there are many possible systems that I would like to keep outside the scope of possibilities, there seems to be a value in persistently choosing different ways. It might well be that a world that does not collapse into ruin anytime soon would be "a world in which many worlds fit".
* stochastic means it includes random effects.
It is unclear to me what you mean here. I have two possible understandings:
(1): You claim if U(t) does not go to zero (eg a constant U(t)=1 because people keep living happy lives on earth) then the integral diverges. If this is your claim, given your choice for p(t) I think this is just wrong on a mathematical level.
(2): You claim if U(t) grows exponentially quickly (and grows at a faster rate than the survival probability function decreases), then the integral diverges. I think this would mathematically correct. But I think the exponential growth here is not realistic: there are finite limits to energy and matter achievable on earth, and utility per energy or matter is probably limited. Even if you leave earth and spread out in a 3-dimensional sphere at light speed, this only gives you cubic growth.
I still think that one should be careful when trying to work with infinities in an EV-framework. But this particular presentation was not convincing to me.