Summary: Arif Ahmed’s Evidence, Decision, and Causality (2014) is a dense, mathematical book-length argument against causalism and for the merits of evidential over causal decision theory. It’s not a light read, so I decided that others, including future me, may benefit from a short, informal summary. I think this summary will be most interesting for people who are new to decision theory. The subsection “EDT Money Pump” may be more generally interesting, unless I’m wrong.

Introduction
Decision theory felt like an unusually obvious personal knowledge gap to me as it plays an important role in s-risk research, some approaches to general AI alignment, and evidential cooperation in large worlds (ECL). ECL in particular only works for cooperators that implement noncausal decision theories (or have particular indexical uncertainty). For them it may have vast moral implications.
Arif Ahmed’s particular thesis allows him to not only argue why evidential decision theory (EDT) lives up to various demands that strike him (and me) as reasonable but also why causal decision theory (CDT) fails to live up to various demands regardless of how reasonable we deem them. These demands can’t serve as reasons to prefer CDT over EDT, so if both decision theories fail them rather than just EDT, that strengthens EDT’s relative position.[1] My interest was primarily in the first type of argument, though, and I may do a bad job at covering the second type here.
Note that the book doesn’t touch on interesting concepts like updatelessness because they’re not distinguishing features of CDT and EDT. If you want to read more about updatelessness, then this 2019 discussion of updateless decision theory is one that I enjoyed, and the 2015 paper “Toward Idealized Decision Theory” sounds exciting!
In the following, page and chapter references refer to Evidence, Decision, and Causality (2014) unless noted otherwise.[2]
I’ve learned a lot from this book and thank Caspar Oesterheld and Johannes Treutlein for recommending it in various articles.
The Book
Arif Ahmed’s own abstract describes Evidence, Decision, and Causality (2014) as follows:
Most philosophers agree that causal knowledge is essential to decision-making: agents should choose from the available options those that probably cause the outcomes that they want. This book argues against this theory and in favour of Evidential or Bayesian Decision Theory, which emphasizes the symptomatic value of options over their causal role. It examines a variety of settings, including economic theory, quantum mechanics and philosophical thought-experiments, where causal knowledge seems to make a practical difference. The arguments make novel use of machinery from other areas of philosophical inquiry, including first-person epistemology and the free-will debate. The book also illustrates the applicability of decision theory itself to questions about the direction of time and the special epistemic status of agents.
So the general structure of the book is this: It argues against a certain doctrine (causalism, defined below) by showing that a corresponding decision theory (CDT) correctly implements this doctrine but that this decision theory ends up making the same or worse recommendations than a rival decision theory (EDT) that ignores the doctrine. So it sets up EDT as the more parsimonious decision theory (e.g., p. 81) that is preferable unless it can be shown that CDT makes better recommendations.
Causalism is the doctrine that rational choice must take account of causal information. Specifically it must attend to whether and how an agent’s available acts are causally relevant to the outcomes that he desires or dreads. …
Evidentialism, which [this book] prefers, is the contrary view that only the diagnostic bearing of acts is of practical concern. It only matters to what extent this or that act is evidence of this or that outcome, regardless of whether the act causes the outcome or is merely symptomatic of it. (p. 1)
The book also explains what recommendations EDT makes in common cause type of decision problems like Smoking Lesion (see A Typology of Newcomb-like Problems) because of the tickle defense; and it clarifies a number of open questions I had about decision theory in general.[3]
There are places in the book where there’s a block of math followed by the words “more formally” and then a longer block of math. But I could generally follow the arguments, so no math degree is needed to make sense of them. Another feature or drawback is of course that it’s written as a defense of EDT for proponents of CDT, so it disproves at length dozens of arguments that never seemed plausible to me to begin with.
But all of that is by design. Most of my knowledge of decision theory now stems from the book, so I’m in no position to critique it in light of its design. Instead I will summarize it and merely comment occasionally when I continue to be confused about some matters.
I also noticed that Ahmed shares my predilection for recondite words like recondite and seems to be generally a chill fellow:
None of the arguments for incompatibilism start to look convincing when I start doing things, and then stop being convincing on reversion to my customary torpor. (p. 218)
Ahmed is a grantee of the Center on Long-Term Risk Fund and attends online seminars of the Global Priorities Institute. (I saw him ask a question in one seminar.) I hope that has resulted and will result in fruitful collaborations on some of the most important questions of our time – in a very long sense of “our time.”
This is how he looks, moves, and speaks. I find it helpful to be able to visualize the author who is speaking to me in some detail.
Responses
Newcomb’s Problem is a 2018 book edited by Ahmed to which he also contributed the introduction and one chapter. I read most of it, and it does contain many new thoughts beyond the purview of the 2014 book. I did not, however, find corrections of any possible errors in Evidence, Decision, and Causality in it. One exception is maybe the chapter contributed by James Joyce (chapter 7, “Deliberation and Stability in Newcomb Problems and Pseudo-Newcomb Problems”), which defends CDT against some critiques in the 2014 book. I haven’t taken the time to understand this reply to the point where I could summarize it.
Chapter 6, “Success-First Decision Theories,” by Preston Greene, is probably the chapter that I would recommend most highly. It fleshes out an “experimental” approach to decision theory that is motivated by a “success-first” criterion of rightness, which sounds synonymous to MIRI’s “winning.” That, I suppose, is all I care about when it comes to my decision theories, so I welcome more academic attention to this criterion. Greene also mentions Functional Decision Theory as an improved version of Cohesive Decision Theory, the latter of which I hadn’t heard of. (Chapter 2, by Chrisoula Andreou, seemed interesting too for its discussion of something called “restraint,” which sounds similar in effect to precommitments.)
Another response (or review rather) that I’ve found is the descriptively titled “Review of Evidence, Decision and Causality” by H. Orri Stefánsson. I have yet to read it.
Game Theory
The first chapter introduces Leonard J. Savage’s axioms from his 1954 book The Foundations of Statistics which entail the principle of strategic dominance: In some games there is one strategy that is better than all others for the player regardless of what happens afterwards, e.g., regardless of how another player responds or how a chance process turns out. The argument goes that it’s the instrumentally rational thing to do for a player to follow the dominant strategy.
Say, you want to build a climbing wall, but you don’t know whether, in the long run, you’ll prefer a vertical climbing wall or one at an angle. You can choose between two climbing wall designs, (1) a rigidly vertical one and (2) a wall that you can tilt to whatever angle you like. All else equal, choosing wall 2 is the dominant strategy because you’ll be indifferent between the walls if it turns out that you’ll prefer a vertical wall, but you’ll be happier with it if it turns out that you prefer a tilted wall.
But there are cases where dominance reasoning leads to funny implications. Say, you’re planning a climbing trip. You’re worried about dying because then it’d be your last climbing trip. You have no rope or harness, so the main risk you’re worried about is from falling and dying upon impact on the ground. But rope and harness cost money, which you could donate to an EA think tank directly or in your will. And a sharp edge might shear the rope, so you’ll die anyway.
You employ dominance reasoning: If you die, you’ll prefer to not have wasted money on rope and harness. If you don’t die, you’ll also prefer not to have wasted money on rope and harness. So either way, you’ll prefer not buying rope and harness, making it the dominant strategy.
Even Alex Honnold would agree that something feels off about this reasoning. The problem is that whether or not you buy rope and harness tells you something about the probability of your death from falling. And this is where decision theory comes in.
- CDT asserts that it’s the causal link from buying rope and harness to the reduced risk of death that makes dominance reasoning inapplicable in this case.
- EDT, on the other hand, asserts that it’s the fact that buying rope and harness gives you evidence (or news) that you’ll have a reduced risk of death that makes it inapplicable.
In this example, CDT and EDT agree (for different reasons) that dominance reasoning is inapplicable.
A few clarifications:
- Decision theory is all about trying to determine what acts are rational. So we start from a position of confusion about what “rational” means and seek to alleviate this confusion. CDT and EDT are two possible ways to define what is rational.
- Decision theory, in this article, is always about subjective probabilities. Ahmed briefly discusses something called “objective decision theory,” but I’ll ignore that here. That means that it’s irrelevant for these thought experiments how terribly wrong the agents may be about the facts of the world but only that their decisions are instrumentally rational given whatever they believe to be true.
- News is a great term for the sort of evidence that EDT is concerned with in that it is only additional evidence that is interesting. A repetition of known evidence is not. This has maybe led to misunderstandings of EDT in the past (p. 88).
- It’s a bit unclear to me what causality actually is or how it would be best defined (if there’s no fact of the matter). I’ve briefly read up on John Mackie’s account of it, but I continue to feel confused about it. Ahmed addresses different attempts to define causation in chapter 6.5 (pp. 157–165). In the following, I’ll assume that an intuitive understanding of it is enough.
Newcomb’s Problem
People have constructed thought experiments to find out whether it’s the evidence or the causal link that is important for dominance reasoning. The most famous one is Newcomb’s problem. A succinct formulation from Wikipedia, citing Wolpert and Benford (2013):
There is an infallible predictor [or, in some formulations, a merely very reliable predictor], a player, and two boxes designated A and B. The player is given a choice between taking only box B [one-boxing], or taking both boxes A and B [two-boxing]. The player knows the following:
- Box A is clear, and always contains a visible $1,000.
- Box B is opaque, and its content has already been set by the predictor:
- If the predictor has predicted the player will take both boxes A and B, then box B contains nothing.
- If the predictor has predicted that the player will take only box B, then box B contains $1,000,000.
The player does not know what the predictor predicted or what box B contains while making the choice.
So the hypothetical outcomes are as follows:
| One-boxing predicted | Two-boxing predicted | |
|---|---|---|
| You one-box | $1,000,000 | $0 |
| You two-box | $1,001,000 | $1,000 |
The reasoning of EDT and CDT respectively, from Nozick (1969):
First Argument [EDT]: If I take what is in both boxes, the being, almost certainly, will have predicted this and will not have put the $1,000,000 in the second box, and so I will, almost certainly, get only $1,000. If I take only what is in the second box, the being, almost certainly, will have predicted this and will have put the $1,000,000 in the second box, and so I will, almost certainly, get $1,000,000. Thus, if I take what is in both boxes, I, almost certainly, will get $1,000. If I take only what is in the second box, I, almost certainly, will get $1,000,000. Therefore I should take only what is in the second box.
Second Argument [CDT]: The being has already made his prediction, and has already either put the $1,000,000 in the second box, or has not. The $1,000,000 is either already sitting in the second box, or it is not, and which situation obtains is already fixed and determined. If the being has already put the $1,000,000 in the second box, and I take what is in both boxes I get $1,000,000 + $1,000, whereas if I take only what is in the second box, I get only $1,000,000. If the being has not put the $1,000,000 in the second box, and I take what is in both boxes I get $1,000, whereas if I take only what is in the second box, I get no money. Therefore, whether the money is there or not, and which it is already fixed and determined, I get $1,000 more by taking what is in both boxes rather than taking only what is in the second box. So I should take what is in both boxes.
So in each case it’s clear what the outcome is for both decision theories.[4] But the dual problem in the field of decision theory is that it’s not only contested how one arrives at a rational decision but also how to recognize a rational decision in the first place: The criterion (or criteria) of rightness is (are) contested too.
A few criteria that I’ve come across:
- Maximal terminal utility (Ahmed’s favored criterion).
- Minimal foreseeable regret (pp. 59, 68, and many more).
- Maximal utility across a probability distribution of all world-histories. (This is my attempt to extract the criterion from UDT 1.0. Does that make sense?)
- Irrelevance of impossible outcomes (not meant to be used in isolation, I think).
To my knowledge, it’s uncontested that EDT maximizes terminal utility in Newcomb’s problem. But using the criterion of minimal regret, one-boxing could be said to foreseeably lead to regret that could be avoided by two-boxing: An agent who one-boxes will be in a world in which there is money under both boxes, so by one-boxing, they miss out on $1,000. Two-boxers, on the other hand, will be in worlds in which there is only $1,000 under both boxes in total and so not miss out on any money under any present boxes. (To me this sounds like a funny form of regret, but that, I suppose, is because I intuitively evaluate things by their terminal utility and can’t fully, intuitively switch into a mindset in which I care only about regret.)
Ahmed discusses regret in the context of the “Why Ain’cha Rich?” argument (ch. 7.3.1, pp. 181–183) and other places (ch. 3.2, pp. 68–73; ch. 7.4.2, pp. 199–201). Apart from the, to me, more interesting arguments for why regret (alone) is not a good criterion, he also shows that CDT leads to foreseeable regret in other cases (e.g., ch. 7.4.3, pp. 201–211), so that it’s in particular no argument to prefer CDT to EDT.
I mentioned above an example in which there is a causal but no evidential effect:
Armour: You are a medieval soldier and tomorrow is the day of the big battle. You have the option to buy a suit of armour for thirty florins. But the predictor tells you that you will be dead by the end of tomorrow. The predictor’s strike rate for this sort of prediction is 99 per cent, whether or not the predictee wears armour. Should you spend what is probably your last thirty florins on a new suit of armour or on getting drunk? (p. 197)
Apart from the prediction there is nothing supernatural meant to be going on in this example. Armour still has a causal effect on protecting you. (Maybe without armor you die within 10 seconds of the start of the battle and with armor it takes a minute?) But the prediction is so good that you gain no consummate evidence of survival from wearing armor. EDT here applies dominance reasoning and recommends getting drunk.
I’m unsure what CDT’s recommendation would be: Ahmed writes in a footnote “it is arguable that Causal Decision Theory itself says nothing about this case, at least not in the present formulation of it.”
Vaguely Newcomb-like Problems
Ahmed’s phrasing is consistent in that it always frames EDT as the more parsimonious alternative to EDT that has to shoulder the burden of proof to show that causal relations are relevant for decision making. (But his arguments don’t rely on that.) The math for deriving an EDT decision was usually simple and the math to derive the CDT decision required a lot more hoop-jumping to get right (e.g., ch. 26–2.7, pp. 48–53). In some cases, deriving the CDT decision required resolving complicated metaphysical issues and hinged on definitorial minutia (ch. 6, pp. 146–165).
But so far nothing has quite convinced me that it wouldn’t be possible for a proponent of CDT to find a different mathematical formalism that makes CDT very simple to work with. Often the intuitiveness of concepts is not so much a proxy for some principled measure such as Kolmogorov complexity but for the inferential distance of the concepts for the particular person working with them. (See also this draft by Linda Linsefors.) So I share the intuition that CDT is needlessly complex, but I’m not convinced that that’s not just some uninformative personal contingency (that may even be related to why I’m reading Ahmed and not Pearl).
But that said, Ahmed describes the discussion that followed the Newcomb’s problem as follows:
- Intuitions with regard to the correct decision in the Newcomb’s problem diverge. Or as he puts it: “The strange thing about Newcomb’s problem is that there is widespread agreement that it is obvious what the agent should do, but not so much over what that is.”
- Newcomb’s problem – at least in its most obviously credible formulation – is science fictional and currently unrealistic.[5] It follows from observation 1 that you can’t easily argue that Newcomb’s problem is a reason to prefer CDT over EDT (or vice versa if someone disagrees about the parsimony of EDT); and it follows from observation 2 that even if our intuitions were more unanimous, we could still not rely on them very well because they are unlikely to be informed by a lot of experience from evolution, culture, or life (my framing).
So the discussion instead focused on (1) trying to find realistic alternatives over which CDT and EDT disagree and showing that one makes a better recommendation than another, or (2) argue against the veracity or relevance of these observations and show that one decision theory makes a better recommendation than another in the original Newcomb’s problem.
Chapters 4–6 respond to the first line of argument. Chapter 7 responds to the second.
Tickle Defense
Predictions are not the only way in which a noncausal effect can emerge. Another purported way is for your action and the outcome to have a common cause. Ahmed argues that these types of setups fail in that they don’t elicit different recommendations from EDT and CDT. A helpful illustration from A Typology of Newcomb-like Problems:
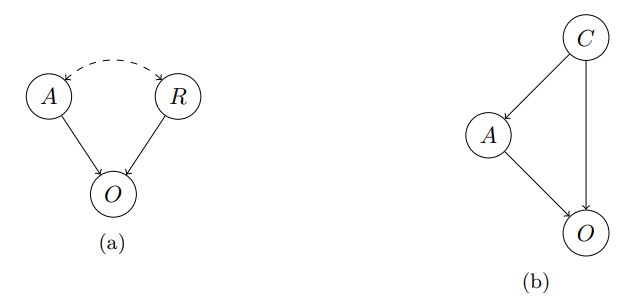
The first graph shows a reference class problem like Newcomb’s problem; the second one a common cause type of problem like the one in this section. A is the action, O is the outcome, R is the reference class (e.g., you in the Newcomb problem), and C is the common cause. The dashed line indicates a noncausal relationship.
A prominent example:
Smoking Lesion: Susan is debating whether not to smoke or to smoke. She believes that smoking is strongly correlated with lung cancer, but only because there is a common cause – a lesion that tends to cause both smoking and cancer. Once we fix the absence or presence of this lesion, there is no additional correlation between smoking and cancer. Susan prefers smoking without cancer to not smoking without cancer; and she prefers smoking with cancer to not smoking with cancer. Should Susan smoke? It seems clear that she should. (p. 90)
I’ve noticed three problems with this thought experiment that often need clarifying:
- Some friends of mine abhor smoking so much that they have trouble accepting the hypothetical that Susan actually enjoys it. This is similar to the problem that the True Prisoner’s Dilemma solves. If you have this problem, just mentally rephrase the Smoking Lesion to be about chewing gum or, if you’re like a colleague of mine who hates chewing gum, maybe ice cream or potato chips.
- It’s sometimes hard to accept the hypothetical that smoking does not directly cause lung cancer because it does in the real world. Maybe that also gets easier with chewing gum or ice cream. (Subjective decision theories are about subjective beliefs that can be perfectly false. So a thought experiment can posit that an actor has any false but consistent belief whatsoever. I don’t think my friends had trouble accepting that but had trouble accessing their intuitions for a highly counterintuitive situation.)
- Personally, I had the problem that, in fact, it did not seem clear to me what to do in this instance! I seemed to have been the exception to “everyone agrees that Susan should smoke in Smoking Lesion.” I understood the tickle defense better when I discovered why that intuition was not more widely shared. More on that in the comment.
It was important for me to realize that this is a problem that is designed to be realistic. So what Susan considers realistic is probably along the lines of this:
The more plausible hypothesis is that the lesion produces smoking via its effect on the agent’s desires and beliefs. We are familiar with cases of this sort. For instance, real life offers plenty of cases in which prior states of the person affect his present desires. Smoking itself is thought to increase the desire to smoke by activating the mesolimbic or ‘reward’ pathway. Something similar may be true of many addictive drugs. (p. 93)
But there’s a tension here. To see where it lies, it is helpful to divide the decision process into three phases: (1) the situation before the decision, characterized by pre-existing desires and beliefs; (2) the decision theoretic derivation of the decision, so here the application of CDT or EDT; and (3) the execution of the decision.
The above description of what a realistic effect of the lesion might be is such that it affects phase 1 but not any of the later phases. In particular it does not bear on how you think about decision theory. Therefore, the very exposition of Smoking Lesion already stipulates everything (desires and beliefs) that is at all evidentially relevant to the decision. The output of the decision theory (being fully and, together with the algorithm, exclusively dependent on the pre-existing desires and beliefs) adds nothing in terms of news. Hence, Susan’s stipulated desire to smoke tells us that she has the lesion with such and such probability. That’s bad news. But the decision to smoke or not to smoke adds nothing to that. So CDT and EDT both advise Susan to smoke.
Ahmed puts it as follows. For his detailed arguments for why it’s sensible to suppose that these apply to the Smoking Lesion and a number of similar problems, see ch. 4.3.
(4.7) Mental causation: the undesirable event produces the dominant option via and only via its operation upon the agent’s current predecision desires and beliefs.
(4.8) Transparency: the agent knows enough about her own current desires and beliefs to make the dominated option evidentially irrelevant to them.
(4.9) Therefore, the agent takes neither option to be evidentially relevant to the undesirable event. (Ch. 4.3, p. 91.)
Treutlein and Oesterheld (2018) put it this way – and also add a paragraph of explanation that I’ll omit here:
(5.1) A rational agent’s action can be caused by modifying (i) the agent’s beliefs, (ii) the agent’s desires, and (iii) the agent’s decision algorithm.
(5.2) An agent employing EDT has sufficient knowledge of (i) and (ii) to make their actions evidentially irrelevant to (i) and (ii).
(5.3) Therefore, Newcomblike problems in which a common cause influences only (i) or (ii) (or both) are incoherent.
The only difference to my above explanation and, I think, Ahmed’s is that they argue that “the problem is incoherent, because it stipulates beliefs and desires that an agent will never hold in a realistic version of the problem; in reality, the most efficacious option has highest news value.” I don’t understand why the problem is incoherent as opposed to uninteresting. But I expect there to be a simple explanation that I just don’t know yet.
I have, for simplicity, phrased these arguments in the language of certainty – e.g., that Susan is certain that the lesion works through her desires and not through her decision theoretic deliberation. Ahmed, however, almost always includes calculations of the thresholds of credences in such propositions, credences above or below which his arguments go through. See, for example, pages 105 and 110.
Comment
I mentioned above that my first intuition was that Susan should abstain from smoking. I double-checked that intuition with chewing gum, which I sometimes enjoy, and it remained stable. My problem was that I imagined the lesion as some sort of highly advance toxoplasma that manipulates me over decades all throughout my life: It increases endorphin levels when I think hard; releases disproportionate amounts of serotonin when I discover a highly parsimonious, elegant explanation; and increases cortisol unless I have a lot of external validation for the things I believe. It thereby incentivizes me to look for intellectual communities that put a strong emphasis on simple explanations. And it does all of that with the goal of gradually, over years, shaping my thinking such that I abandon belief in needless crutches like time, space, and causality unless there is very, very strong evidence for their necessity and only reason directly from wave function–related first principles. Then EDT (along with utilitarianism and Haskell) will seem much more appealing to me than alternatives, and the toxoplasma lesion will have a good chance to control my thinking from the first tickle to smoke all the way to deliberating and carrying out the decision.
From what I understand, the tickle defense would, in fact, not apply in such a case and EDT would recommend that I avoid smoking – or try to – in line with my intuition. If I then actually manage to not smoke for a considerable time, I can increase my confidence that I don’t have the lesion.
But the crux for me was that Smoking Lesion was meant to be realistic. I could argue that hallucinogens have systematic longterm effects on openness, which encourages some frameworks of thought (that tend to sound metaphorical and inscrutable to me), discourages others, and changes tribal identification. But that’d be beside the point: Someone could just add to the thought experiment a detailed account of what Susan considers realistic. We’d get a few different variations of the Smoking Lesion, and the Tickle Defense would apply to some and not to others.
Another thought experiment I hear often is the Chewing Gum Throat Abscesses problem from Yudkowsky (2010). Here the original setup with minor alterations:
Suppose that a recently published medical study shows that chewing gum seems to cause throat abscesses – an outcome-tracking study showed that of people who chew gum, 90% died of throat abscesses before the age of 50. Meanwhile, of people who do not chew gum, only 10% die of throat abscesses before the age of 50. … But now a second study comes out, which shows that most gum-chewers have a certain gene, CGTA, and the researchers produce a table showing the following mortality rates:
| CGTA present | CGTA absent | |
|---|---|---|
| Chew gum | 89% die | 8% die |
| Don't chew gum | 99% die | 11% die |
The researchers hypothesize that because people with the gene CGTA are highly susceptible to throat abscesses, natural selection has produced in them a tendency to chew gum, which protects against throat abscesses. … Having learned of this new study, would you choose to chew gum? Chewing gum helps protect against throat abscesses whether or not you have the gene CGTA. Yet a friend who heard that you had decided to chew gum (as people with the gene CGTA often do) would be quite alarmed to hear the news – just as she would be saddened by the news that you had chosen to take both boxes in Newcomb’s problem. This is a case where evidential decision theory seems to return the wrong answer, calling into question the validity of the evidential rule “Take actions such that you would be glad to receive the news that you had taken them.”
I like this version a lot more than the Smoking Lesion because it probably evokes the strong intuitive aversive reaction to the substance in fewer people. It’s also more open-ended because it doesn’t give away the agent’s desire in the setup.
Yudkowsky resolves it in chapter 9.1 of his paper. In my words: If the problem is meant to be realistic, it seems unlikely that a gene could’ve evolved whose effect goes through causing people to seek out a study that hasn't even been around for long enough to have an effect on natural selection. It’s again more likely that the gene influencers desires. So this EDT friend would be reassured if you told her that you never had an unusual desire to chew gum (have never chewed gum at an unusual rate, if you don’t trust your introspection) and have just decided to do so because of the study results. Or else, if you’ve long been a chewing gum addict, then she does have reason to worry, but the study and subsequent decision to continue with the gum chewing doesn’t add to that worry.
Yudkowsky also mentions a complicated “metatickle defense” due to Eells (1984), in which EDT recursively conditions on the current preliminary decision until it reaches a stable point – if I understand the summary correctly. I’ve run into situations where I thought I ought to reason along such lines, but Ahmed’s analysis of the Ramsey Thesis on pages 220–226 makes me think that he would not be sympathetic to this approach. He also does not in fact use it.
Surprisingly, Ahmed has a paper on PhilPapers, “Sequential Choice and the Agent's Perspective,” in which he uses the Smoking Lesion as an example without taking the Tickle Defense into account or even mentioning it. It was informally published there in 2018 after having been edited (according to timestamps in the file) in 2017. So it’s much more recent than the book. (It also uses some exact sentences from the book.) Perhaps he no longer endorses the Tickle Defense for reasons I don’t know of, or he considers such examples to be science-fictional (like my intuitive reading) unless stated otherwise.
Proper Newcomb-like Problems
Prisoner’s Dilemma
Ahmed concludes that the attempts to create realistic Newcomb-like problems through the “common cause” setup have failed. If that were all that can be said on the issue, the case would rest – unsatisfyingly for me – on EDT’s seemingly greater parsimony. But luckily for me, Ahmed did find – and develop too – actual realistic Newcomb-like problems!
One well-known one is the prisoner’s dilemma (or “prisoners’ dilemma” as Ahmed calls it[6]), covered in chapter 4.6, pages 108–119:
Alice and Bob are strapped to chairs facing in opposite directions. In front of each of them is 1,000 dollars. Each must now choose between taking it and leaving it. Each of them will receive 1 million dollars if and only if the other player doesn’t take the 1,000 dollars.
He gives us the payoff table too (M for million, K for thousand):
| Bob cooperates | Bob defects | |
|---|---|---|
| Alice cooperates | M, M | 0, M + K |
| Alice defects | M + K, 0 | K, K |
Here, Ahmed argues, it is realistic for Alice to suppose in some situations that Bob is very similar to her – be it because they’re twins or because the payoffs are so different that even a slight similarity is enough for the following argument to go through. This similarity might be one of their initial intuitions about the game, say, because something about their characters makes them favor cooperation or defection on some belief or desire level. (In which case the Tickle Defense would apply.) But the similarity might also be one of their reasoning processes or of their ways of executing decisions. It’s not important that this is actually the case but that it’s realistic (because the game is supposed to be realistic) for Alice to think it might be so with a sufficient probability.
Given the payoffs of the game, Ahmed calculates that the conditional probability of Bob making a certain choice given that Alice made that choice needs to exceed 50.05% to be worth it in expectation (p. 110).
Ahmed mentions the “false consensus effect” – where people take their own preference to be indicative of how widespread that preference is – as a reason to think that reasoning of this sort is itself widespread. He also argues that this need not be irrational, despite the name “false consensus effect.”
This is bad news in a way: If the intuition is that you should always defect in a prisoner’s dilemma–like situations and EDT in some cases recommends cooperating, that’d be a disproof of EDT. But not if you can show that EDT makes that recommendation only exactly in the prisoner’s dilemma–like situations where it’s correct to do so.
With this realistic example of a decision situation in which EDT and CDT diverge in their recommendations, the argument can no longer be about showing that any situations in which this happens are too unrealistic to be worthy of consideration and then hoping that EDT will prevail on its parsimony alone. Now the argument needs to be about showing that EDT actually recommends the better decision in these divergent cases.
Ahmed argues for this in the rest of chapter 4.6 (pp. 115–119) based on strange discontinuities in CDT’s recommendations. Please read these if you’re unconvinced of the correctness of EDT’s recommendation in proper Newcomb-like problems.
Comment
What also comes to mind is that studies that determine such things as a willingness to pay are generally considered more reliable if the subjects work with actual monetary payoffs that they can keep after the study rather than with hypothetical money. It might be that this is fully due to some effects like social desirability that subjects deem less valuable than certain amounts of real money. But maybe it’s also partially about the deliberation or execution after it’s clear that the study is about real money. (Perhaps this could be tested by picking a context in which this effect is strong and testing a few common explanations like social desirability by changing, say, how many people learn about the subjects’ decisions. If the effect can largely be explained, my hypothesis is wrong. I didn’t try to find out whether such a study already exists.)
But more generally, we routinely trust that study results extrapolate to people who were not part of the study – at least if the study lives up to our quality standards. This trust is usually not considered to be sensitive to whether the subjects had time to think about their choices or had to make them rapidly or while being mentally occupied. It is, however, sensitive to how representative we think the subjects were of some population or other and how many were employed. Extrapolations from one’s own person, a sample of one, require very high representativeness to make up for the extremely small sample size.
Even more generally, it seems to be common for me and among friends of mine (and with all the topical caveats about external validity also maybe the rest of humanity) to reason like so: “I want to do X. Would Bob mind if I do X? He’s on the phone, so I can’t ask. Would I mind if Bob did X? Not really. So it’s probably fine if I do X.” I usually adjust this line of reasoning for differences between me and Bob that I know about. But even so it’s probably my own character that does the heavy lifting in this simulation of Bob, not the minor adjustments that I make consciously. I’ve found this to be viable when I know the other well or we’re very similar, and when I know that we share relevant knowledge.
The last reservation feels particularly interesting: If I wonder whether Bob would mind if I ate some of his blueberries, the outcome might be (1) Bob would mind, but (2) he wouldn’t mind if he realized just how much I love blueberries. If I suppose that I told him about it weeks ago, then I think it’d be realistic for me to suppose that he’d probably remember it but only with a delay. So he would start out in state 1 but switch to state 2 after a few seconds of reflection. This would make me more hesitant to eat his blueberries. But up the ante sufficiently – say, I’d pass out without blueberries – and I’d still eat them. (Not all of them of course. Just enough not to pass out. I’m not some mean meany-pants blueberry stealer person!) This seems to me to resemble the step from simulating desires and beliefs to simulating a reasoning process too.
Betting on Past and Laws
But Ahmed didn’t stop there! The book also includes contributions of his own that he had separately published as the papers “Causal Decision Theory and the Fixity of the Past” and “Causal Decision Theory: A Counterexample.” Again Alice has to make a hard decision:
Betting on the Past: In my pocket (says Bob) I have a slip of paper on which is written a proposition P. You must choose between two bets. Bet 1 is a bet on P at 10:1 for a stake of one dollar. Bet 2 is a bet on P at 1:10 for a stake of ten dollars. So your pay-offs are as in Table 5.1. Before you choose whether to take Bet 1 or Bet 2 I should tell you what P is. It is the proposition that the past state of the world was such as to cause you now to take Bet 2. (p. 120)
Table 5.1 is as follows:
| P | ¬P | |
|---|---|---|
| Take bet 1 | 10 | −1 |
| Take bet 2 | 1 | −10 |
Ahmed describes this version of the thought experiment as “completely vague about (a) the betting mechanism, vague and slightly inaccurate about (b) soft determinism, and slightly inaccurate about (c) the content of P.” He then constructs a (superficially strange) version of it that is not vague and inaccurate like that, and defends all these choices. Still the above is more intuitive, so I’ll skip over the clarifications.
CDT observes that Alice can’t affect the past state of the world, so that dominance reasoning applies. And because of the particular odds ratios, bet 1 always dominates bet 2 (see p. 126). But that means that Alice would take bet 1 thereby betting that she’s determined to take bet 2. That’s of course patently false in that case and would lose her $1.
EDT, on the other hand, would observe that the payoffs of 10 and −10 are impossible to realize so that bet 2 promises the good news of winning $1 and bet 1 promises the bad news of losing $1. So it recommends that Alice take bet 2.
Ahmed in particular contrasts the following principles:
(5.13) Causal dominance: The dominance principle applies whenever the relevant events are causally independent of the agent’s options.
(5.14) Nomological dominance: the dominance principle applies only when the relevant events are nomologically independent of the agent’s options.
(“Only when” in the definition of nomological dominance I take to mean really only “only when” and not “only and exactly when.” After all, in maybe most cases it’s uncontroversial that there’s no way to apply dominance reasoning.)
A second thought experiment is Ahmed’s Betting on the Laws:
The next day Alice faces a second problem.
Betting on the Laws: On this occasion and for some irrelevant reason, Alice must commit herself in print to the truth or falsity of her favoured system of laws [L]. She has two options: … to affirm [L]; that is, to assert that our world in fact conforms to the (jointly) deterministic generalizations that it conjoins; and … to deny it; that is, to assert that at some time and place our world violates at least one of these generalizations. (p. 130)
The paper “Causal Decision Theory: A Counterexample” makes another stipulation more salient than the book. My intuition was that Alice’s “favoured system of laws” L (it’s called L* in the book but that seems redundant here because I’m not using L for anything yet) is one that she has, say, 30% credence in, with the remaining 70% equally distributed over 10 other systems of laws plus the hypothesis that the correct system of laws is still unknown. But that is not how this is meant. Somewhat unrealistically, Alice is assumed to have almost 100% credence in L. More realistically, the argument goes through if she has > 50% credence in it, if I’m not mistaken. From the paper, but the italics are mine:
Causal Betting Principle (CBP): If you face a choice between a unit bet [the sort of bet we’re dealing with here] on P and a unit bet on ¬P, and if you are certain that P is causally independent of your bet, and if you are much more confident of P than of ¬P, then it is rational to take the unit bet on P and irrational to take the unit bet on ¬P.
The payoff table is even simpler than the Betting on the Past one:
| L | ¬L | |
|---|---|---|
| Affirm L | 1 | 0 |
| Deny L | 0 | 1 |
Ahmed’s argument has two parts, the argument that it’s rational to affirm L and the argument that CDT recommends denying L. I don’t see a reason to doubt that affirming L is rational given the intuition from the causal betting principle above. EDT, according to Ahmed, recommends exactly the intuitive thing.
But I continue to be puzzled over some aspects of the proof that CDT endorses denying L. I say “endorses” because Ahmed’s argument only implies that CDT is neutral over affirming or denying L. In a footnote in the paper he notes: “Strictly speaking, I haven’t shown that CDT strictly prefers [denying L to affirming L] but only that the converse is false. But this is enough to condemn CDT: endorsing an irrational option is just as bad as preferring it to a rational one. In any case, the fact that CDT does not prefer [affirming L] … implies that it does strictly prefer [denying it] given an arbitrarily small incentive to [deny it].”
The argument seems to be along the lines of: CDT forbids conditioning on whether L is true because the laws of nature are very much out of anyone’s causal control. What remains is Alice’s credence that L implies that she’ll take one or the other of her available options. Ahmed’s calculation is perfectly parallel for both of these cases implying no preference for one over the other. And so CDT is neutral about the choice or, as he puts it, endorses denying L (just as it endorses affirming L).
The part I don’t understand is where Alice’s credence goes that L implies that she’ll take one option or the other. In the paper, the credence doesn’t factor into the calculation in the first place while in the book it features in footnote 13 on page 132 but then cancels out (or otherwise disappears) in the last one or two steps, which I don’t understand. But intuitively, I suppose, it’s unrealistic that Alice, as an embedded agent, can deduce a credence for an action of her own from L. This strikes me as something that should only be possible in exceptional cases. So I’m not particularly motivated to investigate this further. (Besides, I’m way over my timebox for this chapter’s summary.)
Comment
Ahmed writes that “This argument for nomological over causal dominance is a special case of a more general argument for evidentialism.” It’s certainly an argument against causalism, which is his whole project. But I suppose evidentialism could still be incomplete, or the argument in particular could be used by someone who prefers to two-box in Newcomb’s problem to argue for something like ”nomological decision theory.”
Quantum-Mechanical Cases
In chapter 6 (pp. 146–165), Ahmed assures us that Mermin (1981) assured him that the following setup is realistic: There’s a source and two receivers A and B. In each run, the source emits two signals to the receivers. It has no switches and receives no signals. The receivers, however, have switches that you can set to 1, 2, or 3. The receivers can’t communicate with one another or, as mentioned, with the source.
The receivers have displays where they display “yes” or “no,” so the outcome of a run can be denoted as 12ny. What looks like a street in New York City, denotes that receiver A was set to 1, B to 2 and the readings on them were “no” and “yes.”
What’s surprising about the setup is that the following statistical observations obtain:
- Whenever the switches on A and B are on the same setting (i.e. both on 1, both on 2 or both on 3) the devices display the same reading: either both say ‘y’ or both say ‘n’. So we sometimes get runs like this: ‘11yy’, ‘22yy’. But we never get runs like this: ‘22yn’, ‘33ny’.
- When the switches on A and B are on different settings (e.g. A on 1, B on 3), the devices display the same reading about 25 per cent of the time. So we get runs like ‘12yn’ and ‘23ny’ about three times as often as we get runs like ‘12yy’ and ‘13nn’.
The first observation could obtain if the receivers just always displayed yy (or always displayed nn) or displayed something in accordance with a specification in the signal. But the second one requires that they switch outputs, and that’s where the behavior starts to look spooky in ways that are perhaps explained by books like Something Deeply Hidden (though this particular device is not mentioned). Ahmed argues for this on page 158, citing John Stewart Bell.
In Ahmed’s book it is assumed that there is no causal connection here, in the intuitive sense of “causal”:
Causal independence: whatever happens at either receiver is causally independent of anything that happens at the other.
This leads to a money pump against CDT that is based on CDT’s refusal to take the distribution of chance events into account because it is causally independent of one’s choices. The payoff table looks as follows where “het” is short for “ny or yn” and “hom” is short for “yy or nn.”
| yy | yn | ny | nn | |
|---|---|---|---|---|
| 12hom | 2 | 0 | 0 | 2 |
| 13hom | 2 | 0 | 0 | 2 |
| 23hom | 2 | 0 | 0 | 2 |
| 12het | 0 | 1 | 1 | 0 |
| 13het | 0 | 1 | 1 | 0 |
| 23het | 0 | 1 | 1 | 0 |
That is, there are no options with identical receiver settings, and a winning bet on any of the “hom” options pays twice as much as a winning bet on any of the “het” options.
For EDT the case is clear: “het” results are three times as likely to come up than “hom” results, so the doubled payoff does nothing to make bets on “hom” more attractive.
The derivation of the CDT recommendation spans pages 150 to 155 and is based on CDT foundations that I haven’t even introduced in this summary, so I’ll skip to the end: “EDT recommends only 12het, which gets a V-score 0.75 over 0.5 for 12hom. CDT endorses 12hom, which is getting some unknown U-score that is no less than U(12het).” (Ahmed chose the ”12” setting in a “without loss of generality” type of move.)
So again we have a case where CDT is neutral between options even though one (or one set) is intuitively better than another.
The objections section of this chapter (almost every chapter has one) is particularly interesting because it goes more in depth on the arcana of how different scholars have attempted to define what causality is. This is something I would’ve found interesting for every derivation of a CDT recommendation, though Ahmed probably omitted them in many cases because the leading definitions don’t disagree on the recommendation.
Ahmed lists the definitions or accounts of causality of Reichenbach, Suppes, Hume, Mill, and Mackie as ones that support a view according to which the correlation between the outputs of the receivers could be called causal – but only if we ignore the requirement of the first four definitions that the cause needs to occur prior to the effect in sidereal time or, in Mackie’s case, logical time, and doesn’t require faster-than-light propagation (p. 159). Lewis’s definition makes it plausible with fewer reservations (ibid.). Under these definitions, CDT will make the same recommendation as EDT.
Salmon, Menzies and Price, Woodward, and Hausman have proffered definitions according to which there is no such causal loop between the receivers (ibid.).
Skyrms’s “family resemblance” theory of causation is silent on the issue (p. 161).
CDT’s neutrality between the options seemed to me to imply that any CDT agent with some nonzero credence in the hypothesis that there may be something causal going on between the receivers will have a tiebreaker in favor of the EDT recommendation. That there is some normative uncertainty about what causality really is – if there’s a fact of the matter – seemed to imply to me that CDT agents would typically have such uncertainty.
But to the contrary, Ahmed shows in chapter 6.5.2 that even in that case, the payoffs of the “hom” options can always be adjusted such that a CDT agent with any degree of uncertainty will (also) endorse the option that EDT recommends against.
Comment
The device is realistic, so Ahmed even offers a challenge:
On your turns, I pay you what you win. On my turns, you pay me what I win. So if I follow EDT and you follow CDT then I will on average win one dollar from you every four runs. I hereby publicly challenge any defender of CDT who accepts [the causal independence premise] to play this game against me.
This seems risky. A defender of CDT can pretend to just “arbitrarily” choose the more lucrative option at every turn. Since CDT is still the dominant view among decision theorists, they can thereby effectively filibuster Ahmed and slow or reduce the chance of a development away from the status quo. (Not that anyone would actually want to do that.)
Page 162 has a very interesting footnote that I’ll reproduce here in full since I’ve not yet followed up on it, i.e. read at least Hilary Greaves’s paper. (Links are mine.)
I have in this discussion altogether ignored the ‘many-worlds’ theory according to which all possible results of any run appear in one of the branches into which the world divides after the readings have been taken (Blaylock 2010: 116–17). One reason for this is that it is hard to see what any decision theory should say about a case in which the uncertainty of each run gets resolved in different ways according to equally real future counterparts of the experimenter: in particular, it is not clear to me why the ‘weights’ that the many-worlds theory attaches to each branch should play the decision-theoretic role that subjective uncertainties play in cases of ‘single branch’ decisions under uncertainty (for reasons arising from Price’s (2010) comments on Wallace 2007 and Greaves 2007). But in any case and as section 6.5.2 argues, anyone who gives the many-worlds interpretation some credence should still agree that EPR drives EDT and CDT apart, as long as he also gives some credence to the ‘single-world’ proposal on which the receivers are causally independent of one another.
This seems to contradict my treatment of measure in ethical decision making, which I’ve so far treated analogously to probability.
Newcomb Again
At this stage, Ahmed has shown that there are various realistic cases in which the recommendations of CDT and EDT diverge. So the disagreement cannot just be due to intuitions that are badly calibrated in situations that are impossible in the real world. This is bad news for EDT, which would’ve otherwise, according to Ahmed, been preferable on parsimony grounds. Or it is bad news for EDT unless it can be shown that EDT actually makes the better recommendations in the divergent cases. Then it may even be good news, since that would constitute an even stronger case for EDT than the one from parsimony alone.
In the first section of the chapter, Ahmed reiterates this reasoning and explains it in some more depth, and in the second, he defuses the “discontinuous strategy” according to which you one-box only when the predictor is absolutely infallible and two-box otherwise, even for (merely) arbitrarily reliable fallible predictors (pp. 170–179).
The Case for One-Boxing
Section 3 focuses on the case for one-boxing and in particular on the “Why Ain’cha Rich?” (WAR) argument (pp. 182–183, I’ve changed the numbering and removed internal references):
- The expected return to one-boxing exceeds that to two-boxing.
- Everyone agrees on 1 (premise).
- Therefore one-boxing foreseeably does better than two-boxing.
- Therefore CDT is committed to the foreseeably worse option for anyone facing Newcomb’s problem.
- Therefore CDT gives the wrong recommendation in the standard Newcomb problem.
The main contentious point about WAR is whether conclusion really follows from statement 4.
One such challenge is due to Joyce (1999), in which he reframes the Newcomb problem as one in which the agent believes to be the “type” of person who two-boxes and believes that this determined the predictor’s decision. This, however, is the type of problem where the Tickle Defense is applicable and CDT and EDT would both recommend two-boxing. (Also if you believe yourself the type of person who one-boxes, because then you can get a thousand dollars extra by two-boxing.) Joyce’s chapter in Ahmed (2018) seems to me like an improved version of this argument.
Next, on pages 187–194, Ahmed addresses an objection due to Arntzenius (2008):
Yankees v Red Sox: The Yankees and the Red Sox are going to play a lengthy sequence of games. The Yankees win 90 per cent of such encounters. Before each game Mary has the opportunity to bet on either side. [The payoffs are as in the table below.] Just before each bet, a perfect predictor tells her whether her next bet is going to be a winning bet or a losing bet. Mary knows all this.
| Red Sox win | Yankees win | |
|---|---|---|
| Bet on Red Sox | 2 | −1 |
| Bet on Yankees | −2 | 1 |
Here, Arntzenius argues, EDT is doomed to always bet on the Red Sox and lose 90% of the time, because if the predictor says that they’ll win their next bet, they’ll win most by betting on the Red Sox and if the predictor says they’ll lose their next bet, they’ll lose least if they also bet on the Red Sox. This would constitute a parallel case to WAR where EDT fails to get rich. (Here a video in case you’re unfamiliar with the sport.)
Ahmed objects that it’s not so much that Arntzenius’s analysis of what EDT would do in this situation is mistaken but that the argument is not parallel to (or a mirror image of) WAR. That seems true enough given the particular syllogisms Ahmed uses, but I have the impression that the more general point stands: The agent who’s been using CDT can still ask the agent who’s been using EDT: Why ain’tcha rich?
Comment
EDT Money Pump
Ahmed argues that Yankees vs. Red Sox is parallel to Check-up (p. 189):
Check-up: Every Monday morning everyone has the chance to pay one dollar for a medical check-up at which the doctor issues a prescription if necessary. Weeks in which people take this opportunity are much more likely than other weeks to be weeks in which they fall ill. In fact on average, 90 per cent of Mondays on which someone does have a check-up fall in weeks when he or she is ill. And only 10 per cent of Mondays on which someone doesn’t go for a check-up fall in weeks when he or she is ill. There is nothing surprising or sinister about this. It is just that one is more likely to go for a check-up when one already has reason to think that one will fall ill. \
…
All weekend you have suffered from fainting and dizzy spells. You’re pretty sure that something’s wrong. Should you go for the check-up on Monday morning? Clearly if you are ill this week, it will be better to have the prescription than not, so the check-up will have been worth your while. But if you are not ill this week then the check-up will have been a waste of time and money.
The payoff table:
| Well this week | Ill this week | |
|---|---|---|
| Check-up | 1 | 0 |
| No check-up | 2 | −1 |
In Check-up it is clear that one can not just calculate the expected return of going and not going to the check-up given the population-wide correlation statistics. The fainting and dizzy spells put you in the reference class of people who are very likely sick, so unless almost the whole population is sick, these broad statistics are uninformative. Rather you can be almost certain that you fall into the “ill this week” group, in which case going to the check-up is the better option.
Ahmed suggests that (1) the population-wide statistics are the equivalent of the long-run Yankees vs. Red Sox statistics, that (2) the fainting and dizzy spells are the equivalent of the predictor, and that (3) the decision is the equivalent of the bet. So there are three variables, as it were.
Ahmed does not consider the population-level statistics to be variable, hence the “as it were.” Whether you’re sick or not and how you decide do not influence these statistics in the limit. In footnote 41 he explicitly says: “So even if she learns that she will win her next bet, is she not still entitled to be as confident in [the statistics] as she was before? … But the point is not that Mary’s information makes [the statistics] false but that [the statistics] no longer [entail] anything about what she should now do. Certainly her next bet belongs to a population of bets of which [the statistics are] true.” That makes a lot of sense.
But early signs of sickness are not sensitive to whether we later go to a doctor. A prediction, given outcomes of games that are held constant, is sensitive to how we bet. So we still end up with two worrisome outcomes:
- An EDT agent will have a predictor who predicts a series of 90% losses. The EDT agent will – EDT-rationally, as Ahmed shows – bet on the Red Sox to minimize the loss.
- A CDT agent will have a predictor who predicts 90% wins. The CDT agent will – ignoring the predictor – bet on the Yankees to maximize unconditional expected value.
So the EDT agent predictably loses money while the CDT agent predictably wins money, and the CDT agent is in a perfect position to ask, “Why ain’tcha rich?” All the EDT agent would have to do is to ignore the prediction.
But I still don’t think Yankees vs. Red Sox is parallel to Newcomb’s problem: The predictor in Newcomb’s problem only predicts your actions. The predictor in Yankees vs. Red Sox predicts the outcome of the game and your bet, two independent events. So in the latter case these two can clash, while in the first case inconsistent scenarios are simply impossible without paradox. (A feature that, to my understanding, MIRI-style decision theories try to capitalize on.)
Consider a robot with no concept of decision theory, money, or utility. The robot follows the simple algorithm to only bet on the Yankees (without loss of generality) unless the prediction is that it’ll lose, in which case it bets on the Red Sox. I’ll call such an agent a “Yankee fan” because they want the Yankees to win every game: The Yankee fan makes worlds in which the Yankees lose inconsistent. Or if the world is malleable, then being a Yankee fan is a way of making sure that the Yankees never lose. (You could get their coach to pay you much more than the payoffs from the bets to follow this algorithm.) But in the following I will assume that the outcome of the game is completely independent.
Say the predictor runs simulations to compute its predictions: At one point it’ll predict that the Yankees will lose. The predictor will run a simulation of the Yankee fan in which they announce that the Yankee fan will win the next bet. They’ll bet on the Yankees. This case is inconsistent. Then they’ll run a simulation in which they tell the Yankee fan that they’ll lose the next bet. They’ll bet on the Red Sox. This case, too, is inconsistent.
But this behavior can be fixed. In a fixed version of the problem, the predictor can choose from three pronouncements: “You’ll win,” “You’ll lose,” and “I don’t know.”
These are the bets of the agents conditional on the predictions:
| You'll win | You will lose | I don't know | |
|---|---|---|---|
| Yankee bettor | Yankees | Yankees | Yankees |
| Red Sox bettor | Red Sox | Red Sox | Red Sox |
| Yankee fan | Yankees | Red Sox | Red Sox |
| Red Sox fan | Red Sox | Yankees | Yankees |
The predictor always (1) simulates the game to determine the winner; (2) runs two simulations in which it announces that the agent will win and lose respectively; and finally (3) announces, in the real world, the overall consistent prediction, one of them if both are consistent, or “I don’t know” if neither is consistent.
| Yankees win | Red Sox win | |
|---|---|---|
| Yankee bettor | You'll win | You'll lose |
| Red Sox bettor | You'll lose | You'll win |
| Yankee fan | Either | I don't know |
| Red Sox fan | I don't know | Either |
Here it becomes clearer why (the the first table) the Yankee fan bets on the Red Sox in the “I don’t know” case (and vice versa for the Red Sox fan). The “I don’t know” case is the one where that team wins. Their chagrin over the lost game will be alleviated by the elation over the won bet. This results in the following expected payoffs:
| Yankees win | Red Sox win | |
|---|---|---|
| Yankee bettor | 0.9 | −0.2 |
| Red Sox bettor | −0.9 | 0.2 |
| Yankee fan | 0.9 or −0.9 | 0.2 |
| Red Sox fan | 0.9 | 0.2 or −0.2 |
- The Yankee bettor makes 0.7 in expectation.
- The Red Sox bettor makes −0.7 in expectation.
- The Yankee fan makes between −0.7 and 1.1 in expectation depending on whether the predictor chooses to announce that they’ll win, lose, or some randomized answer in the case where both are consistent.
- The Red Sox fan makes between 0.7 and 1.1 in expectation for the same reason.
So being a Red Sox fan seems best overall.
Note that the predictor needn’t always run two simulations. It could also run the second simulation only when the first one led to an inconsistent case. This would only change the outcome of the “Either” cases in that they’ll be “You’ll win” or “You’ll lose” depending on which the predictor tests first.
All in all, Yankees vs. Red Sox is similar to the transparent Newcomb problem (as well as the standard version) because that one also has inconsistencies for similar reasons that need to be fixed. But even that likeness seems imperfect to me. The problems behave quite differently (e.g., the predictor is more constrained in Yankees vs. Red Sox if it wants to avoid prediction errors). Or maybe I just haven’t thought of the right way to map one onto the other.
In a related post on my blog I speculate a bit about how such simulation schemes might work and what that says about precommitments and updateless behavior of CDT and EDT in the transparent Newcomb problem.
Better Irrational Than Crazy
On a lighter note: Arntzenius (2008), where Yankees vs. Red Sox originates, argues for Piaf’s maxim, which Ahmed refutes in chapter 3. Arntzenius concludes the section with a mention of the transparent Newcomb’s problem:
Consider again a Newcomb situation. Now suppose that the situation is that one makes a choice after one has seen the contents of the boxes, but that the predictor still rewards people who, insanely, choose only box A even after they have seen the contents of the boxes. What will happen? Evidential decision theorists and causal decision theorists will always see nothing in box A and will always pick both boxes. Insane people will see $10 in box A and $1 in box B and pick box A only. So insane people will end up richer than causal decision theorists and evidential decision theorists, and all hands can foresee that insanity will be rewarded. This hardly seems an argument that insane people are more rational than either of them are. Let me turn to a better argument against causal decision theory.
History repeats itself. It’s ironic how parallel this “argument” is to the one that the standard Newcomb’s problem merely rewards irrationality. I, for one, am happy to be irrational and insane in that sense if Omega pays me enough.
Ahmed also rejects one-boxing in the transparent Newcomb’s problem and argues that this says nothing about the applicability of WAR to the standard case:
A similar point applies to the similar objection to WAR that Gibbard and Harper (1978: 369–70) based on a variant of the Newcomb case in which both boxes are transparent. ‘Most subjects find nothing in the first [i.e. what used to be the opaque] box and then take the contents of the second box. Of the million subjects tested, 1% have found 1 million dollars in the first box, and strangely enough only 1% of those … have gone on to take the 1,000 dollars they could each see in the second box.’ Everyone should agree (certainly EDT and CDT agree) that it would be rational to take both boxes in this case, whatever you see in them. But according to Gibbard and Harper (1978: 371), WAR recommends only taking one box in this modified version of the Newcomb problem. But if it goes wrong here – the argument runs – then there must have been something wrong with it as applied to the standard Newcomb case. But that is not so: the reason it goes wrong here is that the agent has information that puts him not only in the class of people who face this case, within which indeed those who take just one box do better on average, but also within the narrower class of people who face this case and can see 1 million dollars in the first box, if that is what he sees. Within that narrower class, the expected return to two-boxing exceeds that to one-boxing by 1,000 dollars. Similarly if the agent is in the narrower class of people who can already see that the first box is empty. But the fact that nothing like WAR applies in this modified Newcomb case doesn’t stop it applying to the standard Newcomb case, in which no more specific information makes the statistically superior overall performance of one-boxing irrelevant to you.
As of 2018, he doesn’t seem to have quite warmed up to updateless behavior yet. Ahmed in the introduction to his 2018 book Newcomb’s Problem (he is the editor and contributed this introduction and one chapter):
The people who do typically end up rich are the very few who decline to take both boxes even in this case. That seems insane, but these “lunatics” could retort, to the rest of us who have faced this problem: “If you’re so smart, why aren’t you rich?” (For further discussion, see the chapters by Ahmed and Greene.)
The Case for Two-Boxing
This subsection doesn’t so much present completely new arguments for two-boxing than provide more detail on ones that were mentioned throughout the book.
It starts out with the dominance reasoning that I already summarized in the section Newcomb’s Problem. Then it describes something called “information dominance”:
A related but distinct argument for two-boxing imagines that your accomplice has seen what the predictor put in the opaque box and is willing to tell you what it is, perhaps for a fee not exceeding 1,000 dollars. If on receiving the fee he tells you that the predictor put 1 million dollars in the opaque box, your best response is clearly to take both boxes, and both EDT and CDT will recommend that. And if he tells you that the predictor put nothing in the opaque box, your best response is again to take both boxes, as EDT and CDT again agree. So why bother paying the fee? If you know that whatever extra information you are about to get, it will, on getting it, be rational for you to two-box, isn’t it already rational to two-box before you get it? In fact, isn’t it rational to do so even if there is no accomplice?
Ahmed argues that it’s a nonsequitur – i.e. the version with the accomplice and without the accomplice are different problems: “So there is nothing wrong with taking different acts to be rational ex post and ex ante.”
That seems true enough since this problem, too, is equivalent to the transparent Newcomb’s problem. But see this related post of mine on why I think EDT may still one-box even with accomplice or transparent boxes so long as it has a choice to precommit.
The last reason to two-box is “Could have done better” (p. 202):
If you know that a certain available option makes you worse off, given your situation, than you would have been on some identifiable alternative, then that first option is irrational.
I don’t see how this criterion of rightness is different from Piaf’s maxim. Ahmed’s argumentation follows a different structure (if you’re interested in his analysis of sequential choice, see pp. 201–210), but the upshot is the same, namely that this maxim or criterion is a reason to two-box in Newcomb’s problem but that CDT and EDT likewise violate it in different cases so that it is no grounds on which to prefer CDT over EDT.
The Ultimate Contingency
This is a wonderfully opaque title for a chapter that I’ll leave untouched in this summary as a teaser for you to buy the book.
My other reason for omitting it is that it covers a, to me, highly unintuitive and unparsimonious thesis and concludes that the thesis is, in fact, implausible. It leads to CDT and EDT violating such useful properties as dynamic consistency, i.e., that they don’t predictably change their strategy halfway through a multistage decision problem.
Conclusion
I’ve found Evidence, Decision, and Causality to be very insightful and engagingly written. 4.7 out of 5 stars. Sadly, I’m not eligible to write reviews on Amazon.
There are many exciting areas of decision theory that are outside the purview of the book. That may be a reason not to read it, but the book makes it clear from the start what its project is and that it is not intended as a textbook on decision theory. For a non-textbook, though, it’s surprisingly didactic.
In particular its explanation of the Tickle Defense was the most lucid one that I could find. Many other summaries of it that I had read before were very condensed and left many reservations I had unanswered. Ahmed’s explanation answered almost all of them.
My only remaining reservations are that I’m unsure whether the book still reflects the latest knowledge of the author since it’s already six years old and that I wasn’t able to find an errata online.
For example, two people may argue whether plates are better than bowls. One of them may argue that bowls can’t hover in the air while you’re eating. Now the argument may turn on whether this is a reasonable demand, because if it is not reasonable – e.g., if you can always find some surface to put your bowl on to eat or you can always eat with one hand leaving the other to hold the bowl – then bowls may be no worse than plates. But the other party can also sidestep that argument by instead arguing that plates can’t hover in the air either, which works regardless of how reasonable of a demand this hovering ability is. ↩︎
In almost all longer citations I’ve made such alterations as transposing tables, expanding abbreviations, and correcting typos without highlighting them. I’m confident that none of these changed the meaning of the sentences. ↩︎
But you may want to heed the warning of the author that “because of this aim the book couldn’t serve as a stand-alone introduction to decision theory. Anyone who took it that way would find it distorted and lacunary. Distorted because of the focus on the dominance principle at the expense of almost everything else that Savage’s axioms entail; lacunary because of the complete absence from the story of any approach outside the Ramsey–Savage expected-utility paradigm.” ↩︎
If you’re confused about the name “Newcomb’s problem,” imagine all the new combs you can buy from all that money! ↩︎
Clearly, we need a lot more progress in manufacturing technology to produce empty transparent boxes that don’t themselves cost some $20–30. ↩︎
I don’t suppose the naming makes a difference, right? The first version focuses on one of two unnamed prisoners in a parallel situation, so there’s no loss of generality, just like in Ahmed’s version that is explicitly about both prisoners. Sadly, that doesn’t make it any easier to decide on one spelling, so I’ve gone with the more common one. ↩︎
