Summary
I present an extension to my optimal timing of spending on AGI safety model for calculating the value of information of AGI timelines via informing one’s spending schedule.
I show, using my best guess of the model parameters, that for an AI risk funder uncertain between a ‘short timelines’ model and ‘medium timelines’ model:
- Updating from near certainty in medium timelines to short timelines (and following the new optimal spending strategy) leads to a 40% increase in utility.
- Updating from near certainty in short timelines to medium timelines (and following the new optimal spending strategy) leads to a 20% increase in utility.
The gains are greater when considering a model of the community’s capacity, rather than capital.
I also show that small changes in one’s credence in short or medium timelines has relatively little impact on one’s optimal spending schedule, especially when one starts out with roughly equal credence in each[1].
You can enter your own parameters - such as AGI timelines, discount rate and diminishing returns to spending - here.
In an appendix I apply a basic model to consider the opportunity cost of timelines work. This model does not assume novel research is done.
The setup
Suppose you have two ‘models’ of AGI timelines and , with credence in and in [2]. You use your mixture distribution for AGI timelines to calculate the optimal spending schedule for AI risk interventions.
You could do some thinking and come to some credence in and in . How much better is the optimal spending schedule as a result of to the optimal spending schedule as a result of , both supposing ?
Writing for optimal spending schedule according to and for utility of supposing , I compare to (the former, by definition of optimality is greater or equal to the latter).
In the model, utility is the discount adjusted probability we ‘succeed’ with making AGI go well. The maximum utility is where are the AGI timelines and is the discount rate.
Example results for short and medium timelines
I take and as the following, and other parameters as described here. (See the appendix for some basic statistics on the mixtures of and .
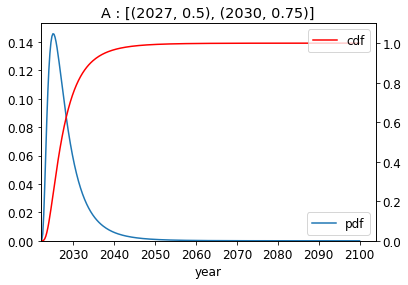 |  |
| : ‘Short’ 2027 median timelines | : Metaculus community timelines (2039 median) |
I compute the results for both the ‘main’ model and the ‘alternate’ model described in the previous post.
- The main model gives the optimal spending rate (in $ per year) for every time step on (1) research and (2) influence (being able to get AI risk reduction ideas implemented).
- Supposing there was only one funder of AI risk interventions, they should follow this spending strategy.
- The alternate model gives the optimal ‘crunch’ rate at each time. At each time point we can either invest in our own capacity (be it through training ,hiring, some types of research, investing) or ‘crunch’ - spend capacity to produce work directly beneficial to reducing AI risk.
- This model gives more abstract results and is more applicable for individuals and teams.
I first show two examples of the optimal spending schedule for each of the models: one that is optimal supposing , short timelines, and one that is optimal supposing medium timelines, .
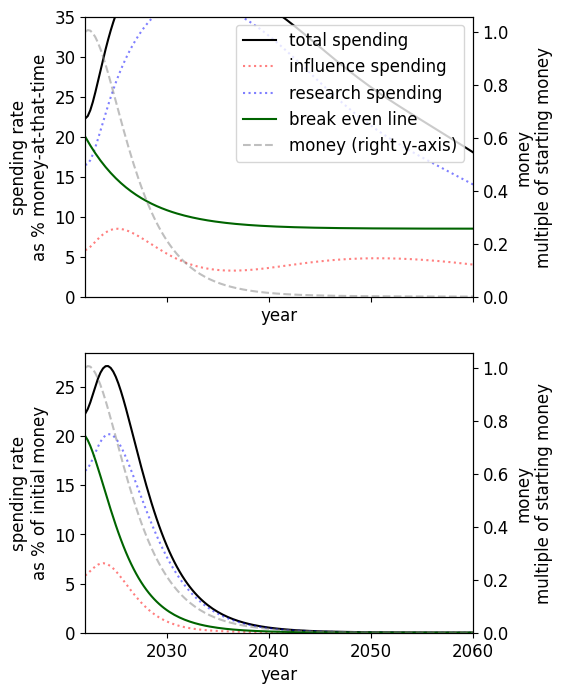 | 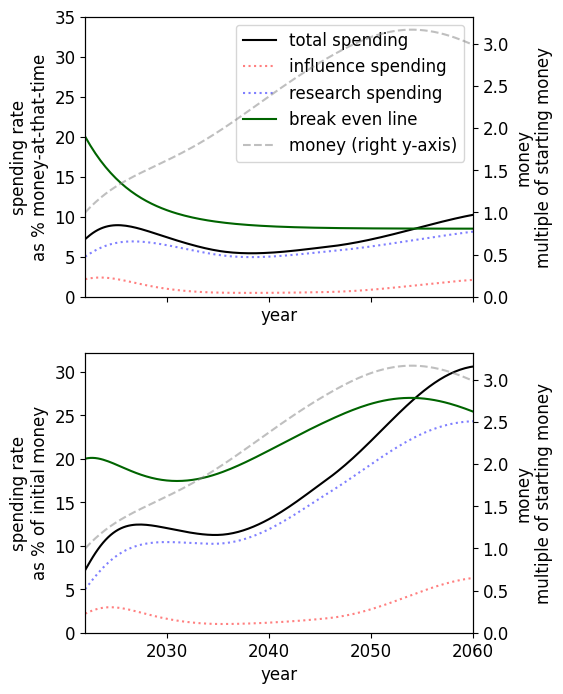 |
Main model The optimal spending schedule assuming , , (left) and the optimal spending schedule assuming , , (right), both assuming medium difficulty. and : going from certainty in to certainty in and following the new optimal spending schedule leads to 20% subjective increase in utility. and : going from certainty in to certainty in and following the new optimal spending schedule leads to 35% subjective increase in utility | |
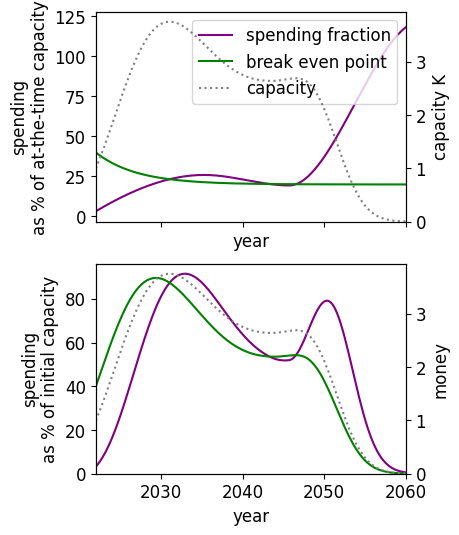 | 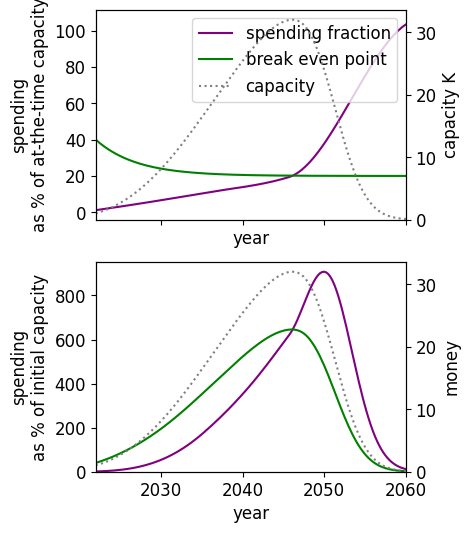 |
Alternate model The optimal spending schedule assuming , (left) and the optimal spending schedule assuming , (right), both assuming medium difficulty. and : going from certainty in to certainty in and following the new optimal spending schedule leads to 18% subjective increase in utility. and : going from certainty in to certainty in and following the new optimal spending schedule leads to 45% subjective increase in utility | |
Results & analysis
Disclaimer: these results are based on my guesses of the model parameters. Further, the models are of course not without limitations. I expect the results to be directionally equal, but lower, for the robust spend-save model. Overall, I’m less confident in these results than the previous spending results.
For each pairing (main capital spending model, alternate community capacity spending model) x AGI success is (easy, medium, hard) I show three graphs. The leftmost plot shows the % increase in discount-adjusted probability of success (utility). The central plot shows this % increase after first factoring out the utilons we get for free - our probability of success if we contributed nothing. The rightmost plot shows the absolute increase in utility.
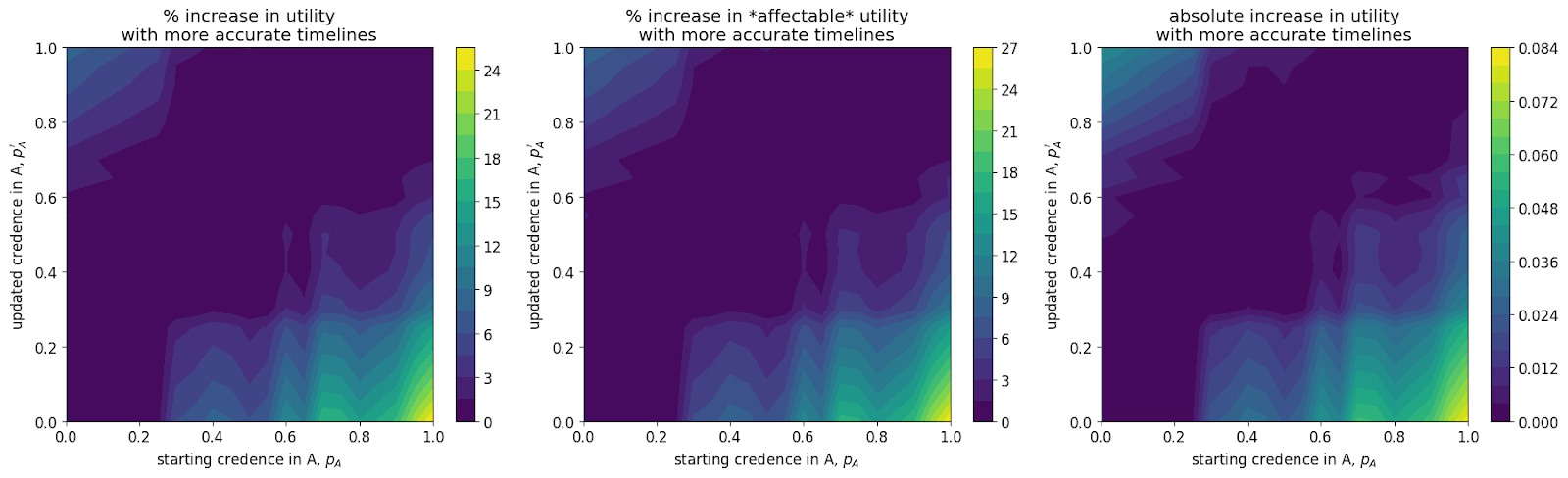
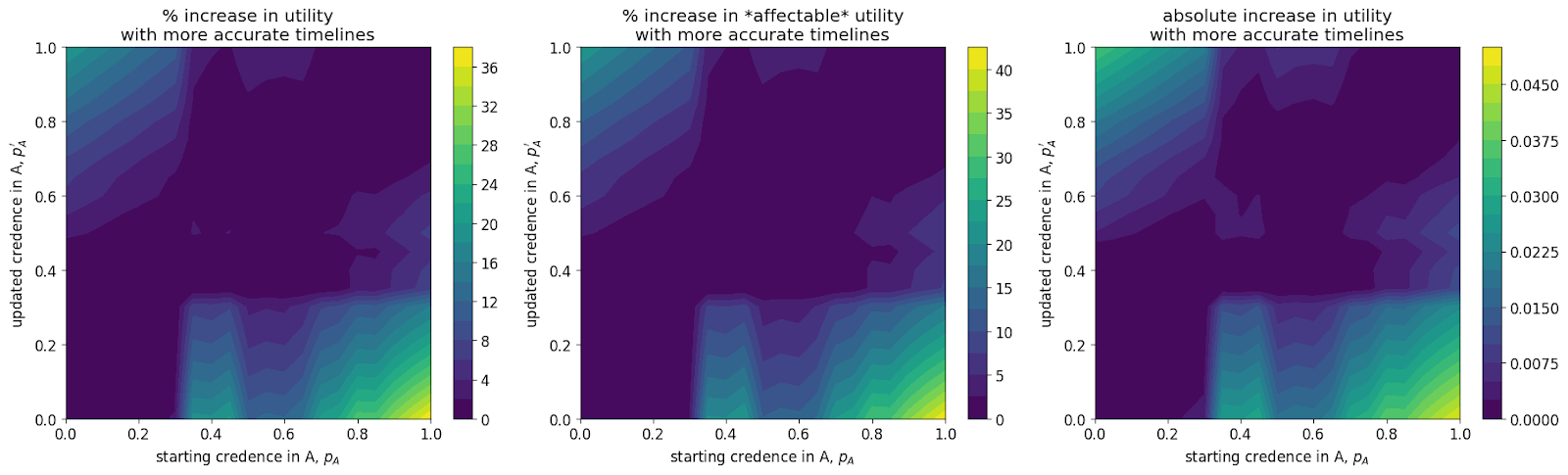
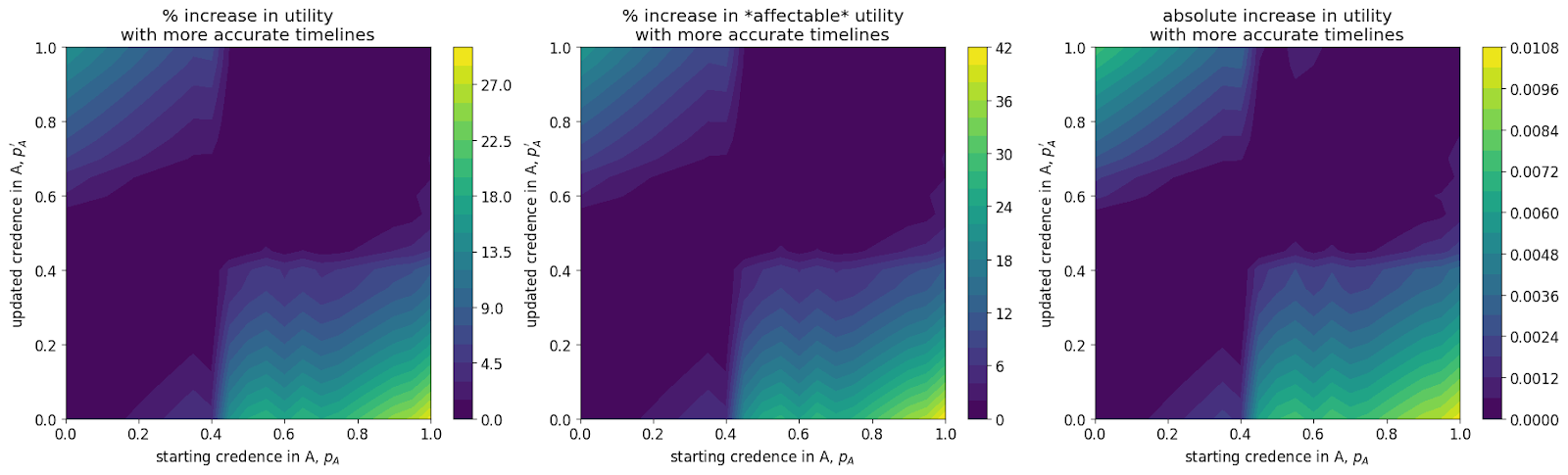
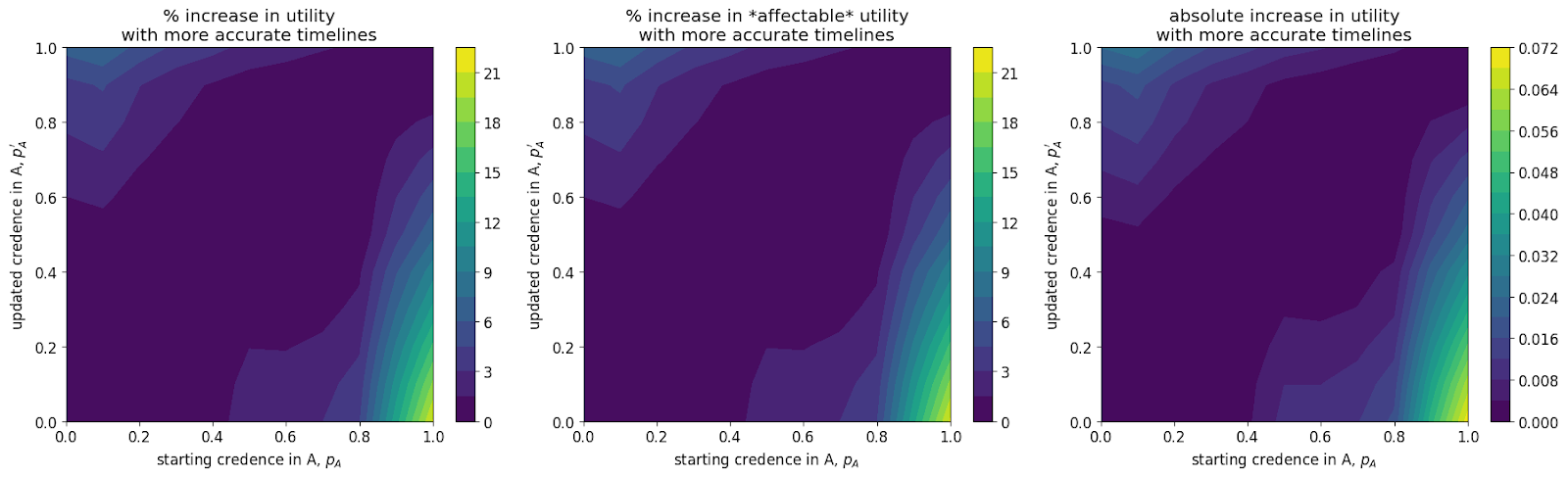
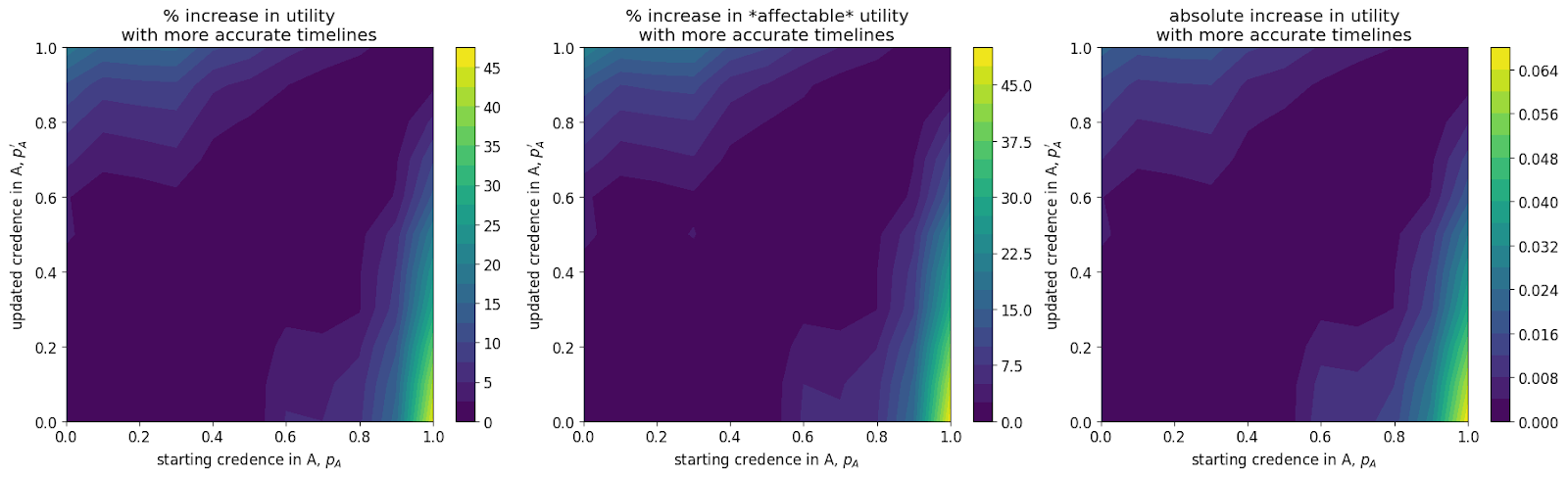
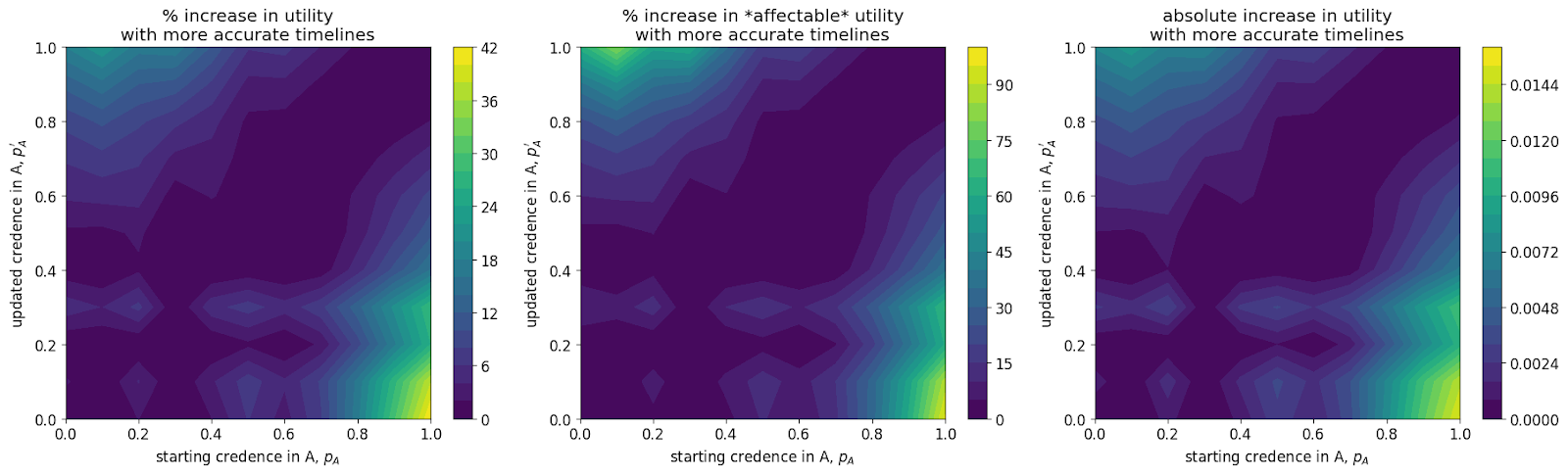
Both the main and alternate model show that:
- The greatest gains are achievable in the hard case where we are highly confident in short timelines but mistaken. The easy case has the lowest gains: this is likely because we can do well regardless of our spending schedule.
- There are greater gains to be had when one is very confident in short timelines than when one is very confident in medium to long timelines,
- The maximum increases in utility are comparable to the gain in utility achieved from the approximate gain the community can make from moving from its current spending strategy to the optimal spending strategy.
- There is little to no gain in utility when one’s credence changes in by less than 10% (this is the bottom-left to top-right diagonal band of purple).
- The main model has greater difference between strategies than the alternate model (compare the examples above) which I believe leads to the rectangular-like areas in the plots: small increases in can push greatly towards early spending.
- The alternate model sees greater utility gains from accurate timelines than the main model. This is likely due to:
- slightly greater marginal returns to ‘crunching’ than there are to spending capital in the main model
- greater opportunity cost of spending early (since there are higher returns to saving).
In practise
Naturally, those with low credal resilience in their AGI timelines have better returns to work on timelines.
The greatest potential gains of timelines work is for people already highly convinced of short timelines. This is particularly true if they are sacrificing gains in capacity now in order to ‘crunch’, or spending at a high rate now (sacrificing a greater amount of capital later). However, it seems that:
- many crunch-like activities may also be building capacity (e.g. building skills necessary for crunchtime), especially because it is relatively neglected in the community
- that the current community spending rate is much lower than the optimal schedule implied even by medium timelines, and so marginally pushing for greater spending is supported regardless of one's credence in short timelines.
In the other direction, the value of information moving from high confidence in medium timelines to high confidence in short timelines are likely to be higher than the results suggest because the current spending rate and crunching rate are too low. That is, if you become convinced of short timelines, your marginal spending/crunching has lower diminishing returns (because, by your lights, the rest of the community is at a suboptimally low spending/crunching rate).
Acknowledgements: thanks to Daniel Kokotajlo for the idea, comments and suggestions. Thanks to Tom Barnes for comments. All remaining errors are my own.
Appendix
Statistics about the mixture of A and B
Potentially useful for calculating your own .
| 25th percentile | Median | 75th percentile | |
| 1 () | 2025 | 2027 | 2030 |
| 0.75 | 2025 | 2028 | 2034 |
| 0.5 | 2026 | 2030 | 2041 |
| 0.25 | 2027 | 2033 | 2051 |
| 0 () | 2030 | 2039 | 2060 |
Toy model
This model is highly flawed but potentially illustrative. Please take it with a massive grain of salt!
Suppose someone deliberates for 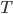 years and updates from
years and updates from  to
to  . Had they not done the deliberation, they would have done
. Had they not done the deliberation, they would have done  years - optimal according to
years - optimal according to 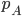 - leading to
- leading to  units of output. After the update, each year they generate
units of output. After the update, each year they generate 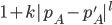 units of output per year. Suppose this last until AGI arrives, which in expectation is
units of output per year. Suppose this last until AGI arrives, which in expectation is 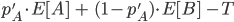 .[9] The person does not regret having done this if
.[9] The person does not regret having done this if
 .
.
Taking 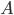 and
and 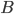 as above,
as above,  and
and  gives the following:[10]
gives the following:[10]
The asymmetry in the plot due to the fact that in the case one in fact has longer than they’d guessed, their impact multiplier applies for more years (this could make sense if there are things you can do down that grow over time, even if in 2042 both the you-who-did-timelines-work-in-2022 and the you who didn’t have similar AGI timelines).
To use these results, one must have a prior over how their credence in A will change over the duration (in expectation it must not change at all though!). Someone with low credal resilience will have a 'wider' distribution than someone with higher credal resilience. One could simplify this step further by supposing discrete credences. For example, one could have 1/4 probability of staying at their current credence in A of 0.6, 1/4 credence in moving to 0.2 and 1/2 credence in moving to 0.8.
The toy model could be greatly improved. For example, one could model the situation as spending non-time resources, in which the above limitation does not occur. Further, one could allow for parallel work on timelines.
- ^
For example, moving from 40-60% credence in short to medium, or vice versa, has very little gains to the optimal spending schedule.
- ^
For example, A is ‘scale is all you need to AGI’ and B is ‘we need more difficult insights’. Or ‘’ is your independent impression, which you could become more confident in, and ‘’ is deference towards others (having accounted for information cascades etc)
- ^
25% probability of AGI going well if it arrived this year, and slope parameter
- ^
10% probability of AGI going well if it arrived this year, and slope parameter
- ^
4% probability of AGI going well if it arrived this year, and and slope parameter
- ^
25% probability of AGI going well if it arrived after a year and the community had been crunching at rate 1 unit of capacity per year (we start with one unit of capacity) and the slope parameter
- ^
10% probability of AGI going well if it arrived after a year and the community had been crunching at rate 1 unit of capacity per year (we start with one unit of capacity) and the slope parameter
- ^
5% probability of AGI going well if it arrived after a year and the community had been crunching at rate 1 unit of capacity per year (we start with one unit of capacity) and the slope parameter
- ^
Assuming is sufficiently small such that conditioning on no AGI in that time makes little difference.
- ^
This roughly approximates the results above
