Acknowledgments
I would like to thank Michael Plant, Matt Lerner and Rosie Bettle for their helpful comments and advice.
Summary
Understanding the relationship between wellbeing and economic growth is a topic that is of key importance to Effective Altruism (e.g. see Hillebrandt and Hallstead, Clare and Goth). In particular, a key disagreement regards the Easterlin Paradox; the finding that happiness[1] varies with income across countries and between individuals, but does not seem to vary significantly with a country’s income as it changes over time. Michael Plant recently wrote an excellent post summarizing this research. He ends up mostly agreeing with Richard Easterlin’s latest paper arguing that the Easterlin Paradox still holds; suggesting that we should look to approaches other than economic growth to boost happiness. I agree with Michael Plant that life satisfaction is a valid and reliable measure, that it should be a key goal of policy and philanthropy, and that boosting income does not increase it as much as we might naively expect. In fact, we at Founders Pledge highly value and regularly use Michael Plant’s and Happier Lives Institute’s (HLI) research; and we believe income is only a small part of what interventions should aim at. However, my interpretation of the practical implications of Easterlin’s research differ from Easterlin’s in three ways which I argue in this post:
- Easterlin finds small coefficients in his preferred regressions of changes in countries’ happiness on changes in GDP. He concludes that these coefficients have low “economic significance” and that increasing economic growth is not a good way to make people happier. However, even if we take these coefficients at face value, they still represent a very meaningful increase in wellbeing within the effective altruism framework, consistent with the impacts of unconditional cash transfers on individuals. The benefits become very large when aggregated across all the people in a country for many years.
- We also have reason to doubt Easterlin’s results, in that they are highly sensitive to small changes in methodology. We perform two variations on his regression that fully accept his methodology of only including “full cycle” countries, but update it slightly, reversing the result. If we replicate his results counting one more country as a “transition” economy, the Easterlin paradox largely disappears. If we repeat his analysis with new data from 2020 instead of 2019, the paradox also seems to largely disappear.
- It may be difficult to find things we can influence whose change over time will have a higher correlation to a country’s change in happiness than changes in GDP. Even if we accept that boosting GDP does not meaningfully increase happiness, other potential means of boosting national happiness may increase it even less. If we rerun Easterlin’s analysis using three interventions Easterlin and Plant suggest (health, pollution, and a comprehensive welfare state), their implied impacts on national happiness are much smaller than the impacts for GDP or negative. However, I have low confidence in this conclusion, and think it is a very valuable project to identify the interventions that are most likely to have an impact on happiness.
1. Taking Easterlin’s results at face value and estimating impact
Easterlin and O’Connor (2022) rely on two regressions for their conclusions, both comparing annual changes in a country’s happiness to annual changes in per capita GDP. The first measures happiness using a “life satisfaction” survey question on a smaller set of countries from 1981-2019 and the second uses a “best possible life” survey question on a larger set of countries from 2005-2019. After excluding some of the countries in the dataset, the authors find that a one percent increase in annual GDP growth rate increases happiness by .001 and .0024 life satisfaction points in the two regressions. They conclude that these coefficients imply that it would take 500-1000 years of one percentage point higher GDP growth to increase happiness by one point, and have low “economic significance.” At first glance, these numbers do seem negligible.
However, once we compare these numbers to what we would expect from the literature on the happiness impacts of cash transfers, we find that they are no smaller than we should expect. Despite being small, these numbers are not exactly 0, and to get a sense of their practical implications we need to convert them to units more familiar in effective altruism. If we want to compare the impact of economic growth to the impact of interventions like cash transfers or deworming, it is helpful to convert the happiness impact of one percentage point higher growth to units capturing the happiness impact of doubling income. In order to do this, we have to consider that it would take 71 years to create an additional doubling of income by boosting growth by one percentage point. Therefore, a doubling of income would produce a 0.07 point increase in happiness using Easterlin’s first regression and a 0.17 point increase using the second. In comparison, HLI’s meta-analysis suggests that providing a cash transfer that doubles income for an individual leads to a 0.1 standard deviation increase in subjective well being. This equates to roughly 0.2 life satisfaction points for the recipient of the transfer. When we use HLI’s methodology to adjust for the fact that other household members likely experience smaller benefits, we get an expected increase of 0.14 life satisfaction points for an average person. So one of Easterlin’s estimates is lower than the impact of a cash transfer, and one is higher. The overall picture appears to be consistent with changes in GDP providing as much happiness as changes in individual income resulting from cash transfers. GiveDirectly, which provides unconditional cash transfers, has historically been one of GiveWell’s top charities, and generally seems like a very good use of money even if it is not the very best.
The happiness impacts of boosting GDP become very large when we take individual impacts that are comparable to GiveDirectly and aggregate them for a whole country for many years. Let us consider the impact of boosting incomes for a whole country with the same population as Ethiopia. We assume that we can find an intervention that boosts GDP growth by one percentage point for 40 years, and that the happiness impacts of this are as small as estimated by Easterlin. Only considering effects over forty years is a fairly arbitrary choice, picked to match GiveWell’s methodology of valuing income increases for 40 years, discounted at 4% annually. I think this is a fairly conservative choice, as some economic research suggests very long-term persistence of changes to GDP. We sum the discounted happiness boost across the entire population. The impact of boosting annual GDP growth from 2% to 3% would produce[2] the equivalent of approximately 400 million person-years of doubled income. HLI and GiveWell each independently estimate that the most cost effective interventions they have identified are approximately 10 times as cost effective as GiveDirectly at improving well-being. Using this multiple, the current costs of GiveDirectly suggest that EA as a community should be happy to spend $10 billion to boost GDP growth in Ethiopia by 1 percentage point for forty years. The amount would be even higher if we incorporated the likely impact of higher GDP on health and education. This is more than ten times as much as all of the money EA is likely to move this year, and likely more than the annual funding of all economics professors worldwide, the IMF, and development economics at the World Bank combined. This does not have any conclusive implications for whether boosting growth in a country like Ethiopia is tractable at these funding levels. However, it does suggest that the well-being benefits are very significant from an EA perspective, in contrast to Easterlin’s interpretation.
2. Easterlin’s estimates of impact become much larger with small changes in methodology.
The previous section looks at the impacts suggested by Easterlin’s methodology if we take it at face value. However, this methodology generates lower regression coefficients than most similarly reasonable alternative specifications. We compare Easterlin’s results with those we get if we rerun his analysis making a different choice about whether we consider India a transition economy, and then by rerunning his analysis with updated happiness survey data. Additionally, we compare Easterlin’s headline results with alternative versions he presents in his paper. These alternative versions of the analysis yield coefficients more consistent with the idea that GDP gains over time yield as much happiness increase as we would expect from cross sectional data than they are with the Easterlin Paradox. Therefore, I don’t think this latest paper should update us much away from the intuitive idea that higher incomes lead to more well being.
Cross sectional data suggests that we should expect a 0.5 point increase in happiness from a doubling in income. If we look at a regression of Cantril Ladder “best possible life” scores against GDP on a log scale, the coefficient implies slightly under 0.5 points per GDP doubling.
Cantril Ladder versus GDP (Sacks et al. 2010)
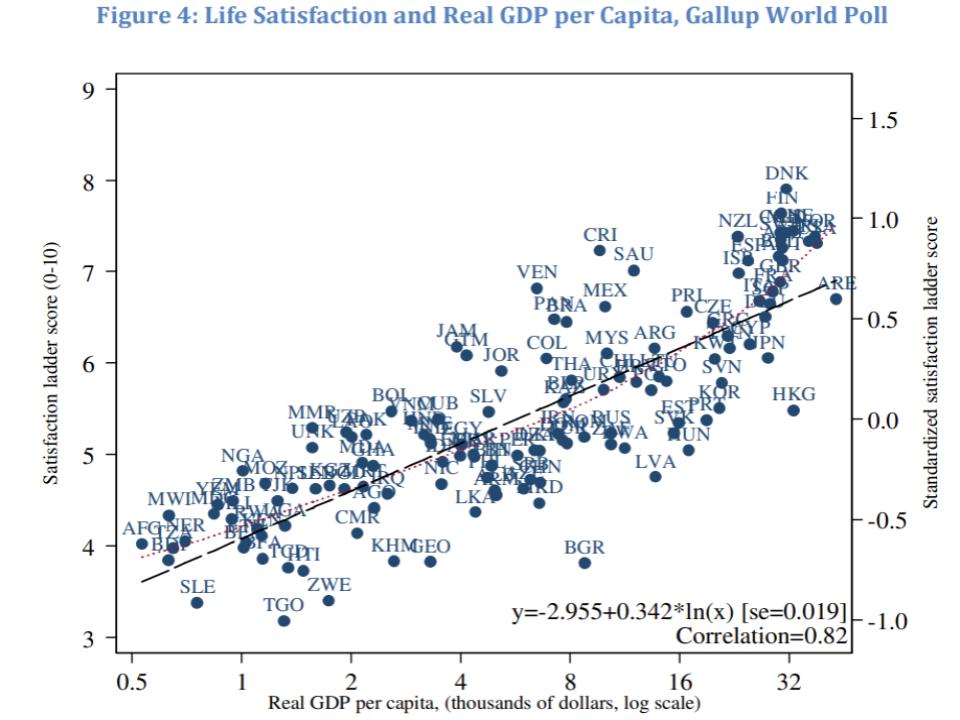
Similarly, if we look at a graph of Cantril Ladder scores for individuals versus their incomes (figure 1 in Michael Plant’s post), we can estimate around 0.5 points per income doubling. In contrast, if we look at Easterlin’s .0024 regression coefficient, it only implies an increase of 0.17 points per income doubling.[3] This is close enough to 0 that it is reasonable for Easterlin to classify it as a paradox when compared to the 0.5 point estimates from alternative sources of data. However, when I rerun Easterlin’s analysis classifying one additional ambiguous case as a transition economy, or using newer data, the coefficients increase. The new results are closer to 0.5 than they are to 0, and don’t seem to imply the existence of a paradox.
Easterlin argues that we need to exclude countries that transitioned from socialist to capitalist economies from our analysis in order to remove the noise created by countries that only start to conduct happiness surveys just as their economies plummet with the start of the transition to capitalism. Most of the countries he excludes are Eastern European, but he also considers China a transition economy. I think it would be reasonable to put India in the same category as China, since both countries experienced a more gradual transition from socialism than did Eastern Europe with the collapse of the Soviet Union. If we repeat Easterlin’s analysis with his data, but exclude India along with China, we get an estimate of 0.3 life satisfaction points per income doubling. So the estimate moves from being closer to 0 to being closer to 0.5 after a minor methodological adjustment.
Next, I replicate Easterlin’s analysis with newly available 2020 “best possible life” scores, instead of the 2019 data in the original paper. In this regression I accept all of his methodological choices about which transition economies to exclude, and how to decide whether a country needs to be excluded for insufficient data. The new regression implies an impact of 0.3 life satisfaction points per income doubling.[4] Once again, this version of the analysis is closer to being consistent with the cross sectional data (0.5 points per income doubling), than it is to a paradox (0 points).
Similarly, if we look at alternative versions of the regressions included in Easterlin and O”Connor (2022), almost all of them have much higher coefficients than the main result. Easterlin makes two key methodological choices. The first is excluding transition economies. For both the “life satisfaction” and “best possible life” regressions, not excluding the transition economies would imply an impact of 0.4 life satisfaction points per income doubling. The second choice Easterlin makes is excluding all countries from the “best possible life” regression that have fewer than 12 years of data available. When he includes the 8 additional countries with 10 or 11 years of data, the impact also goes up to 0.4. I think Easterlin makes good arguments for these two choices.[5] However, I think we have to consider how sensitive his conclusion is to judgment calls when deciding how much to believe that there is a surprising paradox[6] in the happiness data.
3. The happiness impact of alternative interventions is smaller than the impact of GDP.
Easterlin concludes his latest paper by suggesting that even though he does not believe that GDP growth has a meaningful impact on happiness, that there are a number of better interventions. Michael Plant adds some suggestions to the list in his post, coming up with a set of potential interventions that includes:
“...job security, a comprehensive welfare state, getting citizens to be healthy, and encouraging long-term relationships…[taking] mental health and palliative care more seriously…improved air quality, reduced noise, more green and blue space (blue spaces being water), and getting people to commute smaller distances (Diener et al. 2019). Social interactions could be enhanced via urban design, reducing corruption, increasing transparency, supporting healthy family relationships, and maybe even things like progressive taxation.”
All of these sound like promising ideas, and are a good research agenda for future investigation. However, it may be difficult to find one of these measures that has a higher impact on country-level happiness than GDP using Easterlin’s methodology. To perform an exploratory analysis, I start with Easterlin’s data from his “best possible life” regression (taking his relatively low estimated impacts at face value as I do in section 1.) I then choose three interventions from Michael Plant’s list that seem to have a fair amount of annual data available on OurWorldInData.org: health, pollution and a comprehensive welfare state.[7] I replace annual GDP growth in Easterlin’s regression with annual growth on these three metrics, and perform a separate analysis for each one.[8] Each regression looks at annualized changes in a country’s Cantril ladders scores versus annualized changes in the specified metric for the past 12-14 years. The health regression estimates how much a decrease in the number of years people in a country lose to ill health corresponds to increases in happiness. This regression produces coefficients that are either an order of magnitude smaller than the GDP regression, or negative, depending on whether we exclude countries that have less than 12 years of data. In both cases the r-squared of the regression is essentially 0.. There does not appear to be a way to interpret these results to suggest that changes in health have a higher impact on national happiness than changes in GDP. The pollution regression repeats the methodology for health, but looks at only the changes in the years of life lost to pollution. This analysis actually shows negative results of a magnitude similar to the positive results of the GDP regression. This would imply that increases in pollution are actually associated with countries getting happier. For example, the Republic of Congo and Benin both had large annual increases in happiness despite increasing levels of pollution.[9] The comprehensive welfare state regression examines the impact of changes in a score of whether a country has an adequate safety net. This analysis also shows negative results, however there are very few countries and years for which this data is available and the data appears to be of low quality, suggesting that we should not read too much into this result. In all three of these analyses we do not find any evidence consistent with any of these metrics having a higher impact on national happiness than changes in GDP.
I do not have a high level of confidence in these initial results. There are likely better sources of data, and better methodologies to employ. However, I do think they suggest that it may be difficult to find any interventions of their kind which will imply a larger impact on happiness than GDP using Easterlin’s methodology.
4. Conclusion
Easterlin’s estimates of the impact of GDP growth on happiness are not as small as they initially appear. They are consistent with experimental data from individual cash transfers, and imply large welfare gains when aggregated for an entire country. When I consider slight variations in methodological choices that Easterlin makes, or update his data for 2020, the estimated impacts get much bigger. This leads me to decrease my belief in the existence of an Easterlin Paradox that we need to explain. But even if we accept Easterlin’s estimates, it may be difficult to find other things we can influence that will have a larger measured impact on happiness than GDP growth. I find three of the more promising potential ways to boost national happiness to have a smaller impact than boosting GDP. Of course, other interventions may prove to be far more tractable than boosting GDP, even if they have a lower impact on happiness. Also, we can likely find better sources of evidence than regressions with fewer than a hundred datapoints. So my conclusion is not that different from Easterlin and Michael Plant in that I do think the interventions they propose are very promising routes to explore towards increasing happiness. I just don’t think the data warrants dismissing GDP growth as a potentially even more promising route.
Notes
I use happiness in this post interchangeably with both life satisfaction and Cantril Ladder “best possible life” scores. Easterlin does not discuss measures of affect or other more immediate metrics, so happiness is not meant to refer to those here. ↩︎
This spreadsheet calculation starts with one individual benefiting from increased GDP growth, and assumes that benefits of the GDP growth intervention start accruing after 8 years (just as the benefits of deworming start to accrue 8 years after). On the 9th year, the benefit is the difference between growth of 3% versus 2%, discounted by 4% for 9 years. The benefit is quantified as ln of percent income (to be consistent with GiveWell income boosting CEAs). The 10th year has further growth of the same amount, and is discounted by 4% for 10 years. We continue this estimation for 40 years and sum across all years. We then multiply by 115 million, the population of Ethiopia. The total ln impact is then converted to income doublings by dividing by ln(2). We consider the cost of an income doubling to be 1/10 the $294 GiveWell uses for GiveDirectly. We discount the final result slightly because the average estimated impact in Easterlin’s two regressions is slightly below the impact of cash transfers on happiness. ↩︎
I focus on replicating the Cantril Ladder “best possible life” regression from the Gallup survey within Easterlin and O’Connor because the data is more readily available online than the World Values Survey “life satisfaction” regression. I am also not able to benefit from the longer time series in the World Values Survey because my potential interventions in section 3 have limited historical data. After arriving at regression coefficients, I convert them to “life satisfaction impact of an income doubling” here. ↩︎
The regression is not an exact match to Easterlin’s because I use a different source for GDP, the new dataset includes more countries, and I use a simplified methodology for estimating annual happiness change (I do this because I believe it is more consistent with how we calculate annual GDP change, and for simplicity). However, my 2019 coefficient roughly matches Easterlin’s. ↩︎
The reason that Easterlin excludes economies that have less than 12 years of data and that recently transitioned from socialism to capitalism is that he does not consider them to be full-cycle countries. Easterlin accepts that short term fluctuations in the business cycle have impacts on happiness in the short term. However, he thinks that once we zoom out to longer patterns of GDP growth across an entire business cycle, these impacts disappear. Since economies that transitioned from socialism have generally been growing since happiness surveys for these countries have become available, they have not experienced a full business cycle including a “bust.” Similarly, Easterlin does not consider countries with less than 12 years of data to have had a full business cycle (although he does not specify why the cutoff should be 12 rather than 13 or 11). ↩︎
Easterlin argues that this contradiction can be resolved by considering that people evaluate their lives in comparison to those around them. While this could explain the contradiction with cross-sectional data of individuals within a country, I do not think it does a good job of explaining the cross-sectional data at the country level, or the data from cash transfers. If people were evaluating their lives in comparison to those around them, then people in poorer countries would not be much less happy than people in rich countries at a given point in time (especially in older data sets before the spread of Western media). People would also not get any happier when they and everyone in their village received a cash transfer from GiveDirectly. ↩︎
I proxy health with “DALYs-rate-from-all-causes per 100,000,” pollution with “DALYs-particulate-matter per 100,000,” and a comprehensive welfare state with “adequacy-of-social-safety-net-programs.” ↩︎
I begin the analysis by pulling all happiness scores, and years for which they were pulled from Easterlin’s appendix. In order to estimate the changes in each new metric, I pull data for all available years from OurWorldInData. I then do a lookup for the country-year pairs corresponding to the starting and ending year for each country in Easterlin’s data. Finally, I annualize the changes from the first to last year using the same methodology as Easterlin uses for GDP. I also multiply the annual changes by a factor so that they have the same standard deviation as the changes of GDP, and so that larger numbers imply improvement. I do this in order to have a consistent interpretation of coefficients. However, the conclusions are not sensitive to this methodological choice. ↩︎
Of course, this does not mean that decreasing pollution levels is bad for happiness. The more likely explanation is that higher pollution in low and middle income countries is associated with more industrial jobs and more cars, both of which probably make people happier. Although, surprisingly, controlling for GDP growth does not seem to do much to reduce the coefficient on pollution. ↩︎

Vadim, thanks very much for writing this. I'm really pleased to see this debate moving forward. I've discussed this quite a bit with HLI colleagues over the last few days and wanted to share where we've got to so far.
TL;DRs are (1) We should probably now conclude we don't have enough data to know if the Easterlin Paradox is true; (2) even if economic growth increases wellbeing, the effects are likely so small we should be sceptical about prioritising it.
I'll break this into several smaller points.
1. Easterlin and O'Connor (and others) do not claim there is no relationship between growth rates and happiness. They claim there is one - it's what you pick up on - but that it's not statistically significant (we don't know if it's more than chance) or economically significant. The latter term is a bit vague, but the sense is that it's so small we shouldn't make increasing economic growth a priority.
2. What I take to be your key observation is that, just taking the coefficients at face value, they suggests that (A) doubling of national income over time has about the same effect as (B) doubling income for an individual at a time. Hence, there is no paradox to explain: wealth makes nations as much happier as it does individuals. This observation is important and I think new.
3. One issue, however, is that we lack the statistical power to check if this effect holds. This is a rather large update and I thank Caspar Kaiser for it: Caspar points out the relevant coefficient is 0.001, three times smaller than the standard error. To elaborate, the problem is we're looking for a really small change over time but there are only a few years of available data. By rough analogy, this is a bit like trying to detect if climate change is happening when you have only 100 years of data - because the effect is so small, you'd struggle to detect if even if it's there. The effect on long-run growth might be more positive, or even negative, but we cannot tell.
4. As far as I know, no one has raised this issue regarding the Easterlin Paradox either: namely, because the (cross-sectional) relationship between income and happiness is so small, would we actually have enough data to prove or disprove the effects over time? I think this merits further investigation and it would be worth calculating when there would be enough data to tell.
5. One thing that's worth (re)emphasising is how small the relationship between income and happiness is. If a doubling of income increases subjective wellbeing by 0.1 on a 0-10 scale - what HLI's cash transfer numbers suggest - then you need 10 doublings to go up 1 point. However, that means you need to be over 1,000 times richer. If we're thinking on a global scale, extrapolating this far starts to look weird: what would the world be like if global GDP was 1000x was it is right now? Is that even possible? Relatedly, we should worry about how reasonable it is to look at the 2-3 decades of data we have about economic growth and extrapolate that forward 500-1000 years.
6. On the basis of 5, you can see why Easterlin and others have claimed the relationship is economically insignificant: in short, a little bit more economic growth is barely going to move the collective needle, particularly if you're thinking about improving lives over (just) the next 50-70 years (rather than the longterm).
7. A potential response to the claim it's economically insigificant is the one Vadim makes: actually, a small change to a lot of people is a big change, and we should (in principle) be prepared to pay quite a lot to make this happen.
8. I think the correct response to 7. is to agree to the principle that if we could (say) raise economic growth by 1 percentage point for 30 years, that would be quite big, but then to point out there doesn't seem to be a large magic wand we can wave that will make this happen. More generally, I'm not a fan of claims along the lines that "we should be excited about unspecified action X, even if it costs an arbitrarily large sum of money Y, because it's a great deal even if it only has an arbitrarily small chance of success Z". I don't take these seriously until more evidence is provided.
9. Moving on to Vadim's second and third claims, it's not really the case that small differences in methodology make big differences to the results: Caspar Kaiser also pointed out that all of these are super imprecisely estimated anyway, so the particular results from adding or taking one bit away are basically luck.
10. Finally, on the comparisons of increasing GDP vs other things, we really want to get into the details of cost-effectiveness analyses and the success of achieving particular policy goals, rather than just looking in crude terms and how big various changes would be.
On 3., is it worth trying to be more Bayesian? Yes, we face data limitations because there's <200 countries in the world, and the data from most countries is pretty crap. But it feels intuitive (to me, at least) that growth should have some positive effect on happiness, and we have some data from areas, like cash transfers, that suggests more money makes people a bit more happy. And then Vadim suggests that the data we do have suggests a small but slightly positive effect of growth on happiness. So my belief that the studies he refers to are picking up on a real effect rather than pure chance is higher than it would be based on the study's error bars alone.
Personally, I find 7. a compelling response to 5. and 6. We don't need to imagine reductio scenarios of counterfactual effects lasting for a 500 years or 1000x increases in world GDP because even short-lived growth accelerations have large aggregate effects because they affect so many people. Relatedly, I think in practice growth interventions in practice will look less like "increasing economic growth by 0.0001 percentage points" and more like x% chance of sparking a growth acceleration for years or decades a la Pritchett et al. 2016.
What kind of evidence you refer to in 8. would actually change your mind? Why does expected value reasoning not work here?
Michael, thanks so much for really engaging with the post. I think we are now very close in our big-picture views on the subject, but would love to continue the discussion on the more interesting areas of disagreement (I will respond to those points below). I agree that we don’t have enough data to say if the Easterlin paradox holds. I am also somewhat hesitant about prioritizing economic growth as an intervention, although my concerns are less about effect sizes directly, and more about whether generating growth is tractable, and whether potential interventions carry large risks.
I agree with Stephen Clare’s response that we can try to be more Bayesian here. I think it’s reasonable to start with a prior based on the very statistically significant cross-sectional correlation between a country’s GDP and its well-being. In order to believe that this correlation does not generalize to changes in one country across time, we would need to believe that Ethiopia could grow to have the current US GDP but remain as unhappy as a low income country. That would make it an extreme outlier in the cross-sectional data, and would imply that there was some kind of idiosyncratic problem with the country (and I don't think the argument about people comparing themselves to peers deals with this problem). So I think there is some burden of proof on providing evidence that there actually is a paradox. If we start with a prior based on the cross sectional data, we would initially expect a 0.5 life satisfaction point increase for an income doubling. Then we can update on HLI’s meta-analysis results, suggesting that the impacts of cash transfers only have an impact that is a quarter of that. So now we would believe that the impact is somewhere between those two values. Then we get Easterlin and O’Connor’s regression results, which are not in themselves statistically significant. However, they are pretty much the same as the HLI results, so there is no reason to move below the range we believed the effect to be in before. It does not seem to make sense to update all the way to 0 based on results that are non-zero. So even though Easterlin and O’Connor’s regressions do not in themselves have enough statistical power to provide any evidence for their being an impact of growth in happiness, the coefficients they provide should not update us away from what we believed to be the effects of income doubling before. That being said, we have very small datasets here, the individual countries are correlated to each other (making the amount of independent information we have even smaller than it seems), and all of this is simply correlation. We have not done anything here to control for omitted variables, to try to run lagged regressions, or to try quasi-experimental designs. So overall I agree that we should not expect to learn very much about causal impacts from these types of regressions.
I agree with this. And I think the amount of data we would really need would be much higher than it initially seems. Since Easterlin and O’Connor’s are running multiple different statistical tests (deciding exactly how many years of data a country needs before it counts as full-cycle, and separately deciding which countries are transition countries), we would need even more data to make up for the multiple hypotheses.
If we accept the results from the 2020 data, or alternatively assign a probability of 50% to there being no Easterlin paradox, then it would really only be 3-4 doublings to get an additional point of life satisfaction. If we accept the results from HLI’s analysis, I believe it would be about 6 income doublings (starting with 0.1 standard deviations, converting to life satisfaction points, and then discounting for decreased benefits for non-recipient household members)? A country like Ethiopia could have about 6 GDP doublings before getting to United States GDP levels. I would like to thank Matt Lerner for pointing this out.
I agree that we can and should try to be Bayesian but, if we do, we still don't get a slam-dunk result that economic growth will increase average happiness (at least, in already rich countries).
The story that often gets told to explain why the Easterlin Paradox holds refers to hedonic adaptation, social comparison, and evolution. We are very good at getting used to lots of things but we do continue to notice our status relative to others. How much material prosperity do we really need, given humans are basically naked apes who evolved to live in the savannah? We might imagine getting richer would make a difference to us, but think about the last thing you were really excited to buy, then think about how you've stopped paying attention to it. Therefore, we can explain both why money would matter in the cross-section and why it wouldn't matter in the time-series. So noticing that money makes individuals happier at a time does not, by itself, require us to conclude that economic growth would increase average happiness.
What's more, there are some reasons to worry that modernity is not good for humans. As I said in my earlier post:
In other words, you can't just assume that economic growth increases happiness - that's exactly the point. If you're going to already take it as given, then there's no purpose in having the debate.
Michael,
That is entirely fair. It's reasonable to not accept the cross-sectional results as having any information value for your prior. So I should have have said we can start with a prior from the HLI meta-analysis results (which if I remember correctly are pretty statistically significant). Then when we get the information from the Easterlin and O'Connor paper, where the results are the same as our prior, but not statistically significant, to say that the new information does not shift our prior results at all. So even though the Easterlin and O'Connor paper does not give us much information one way or the other, it still seems reasonable to say there is no reason to think that the results are likely to be much lower than the HLI results?
I don't think this makes sense, no, sorry. The HLI meta-analysis results are from cash transfers, which make a few individuals happier over time, not looking at the average of an entire society. It's well-studied that people care about their relative income, not just their absolute income. So we should be particularly worried about extrapolating from what works for individuals to what works for societies - especially where we think the benefit to the individual could be from comparisons. Hence, I think it is not justified to start from the HLI numbers.
IIRC, in the HLI cash transfer meta-analysis, we found that cash transfers had no effect on those in nearby villages ('across-village' effect). In other words, there was, on average, no relative income effect. I was puzzled by it and I find it hard to believe - our CEA does, however, despite my disbelief, assume there are no negative spillovers from cash transfers. I was puzzled by this because there's such consistent evidence of a relative income effect in rich countries. I also thought it was weird the effect from cash transfers was zero. To put this in context, imagine a bunch of people down the road from you get given $40,000 for each household. Would you expect that to have no effect on you? It wouldn't make you envious? Or, it wouldn't make you excited that this might happen to you? I'd expect the effect of income to be (almost) wholly relative in rich countries, but not that there was no relative income effect in the very poor. However, there wasn't loads of across-village data in the HLI meta-analysis, so I didn't update much. It would be good to have a bigger and better analysis of the relative income effect in very poor contexts.
I agree that we have very little evidence so far about the tractability of economic growth interventions. I just think that Easterlin and O’Connor’s work should not make us think that economic growth interventions are any less useful than we would have otherwise thought. Since these sorts of regressions seem to show smaller impacts for health and pollution than GDP, maybe they should (very very slightly) update us towards thinking a little more of economic growth interventions than whatever our prior beliefs were.
I agree that all of the increases in regression coefficients are not that large in some absolute sense, and are in some sense luck. But the increases do seem to be large enough to flip us towards rejecting rather than accepting the Easterlin Paradox. This is statistical luck in some sense, but that just seems to show that the results are very sensitive to that sort of luck. So, as we both seem to agree, we don’t really have enough data to say if the Easterlin paradox holds.
I would love to see more work around estimating the expected costs and impacts of national health, pollution, social safety net, and growth policy on life satisfaction. I suspect that these sorts of change-on-change regressions would not end up being a large part of the evidence on which we based these estimates. Since there is so little data here, we might end up having to rely on judgements about individual policies’ chances of success. My point in the post was simply that Easterlin and O’Connor’s analysis does not seem to give us any evidence to suggest that GDP is likely to be less impactful than health or pollution.
First off, very interesting. This is my first exposure to the EA community. My friends / colleagues have rightly encouraged me to learn more about your work.
Essentially, my argument is this: you cannot believe that the relations we estimate are consistent with cross-sectional results or experimental results because it takes 71 years for income to double when increasing growth. I further explain this below.
I think we agree that GDP is not a good measure of wellbeing. I also strongly believe it is not a good policy target. We should target wellbeing directly.
For alternative policies that similarly cover a long period of time, see recent work by me and Easterlin, "Explaining happiness trends in Europe" (https://doi.org/10.1073/pnas.2210639119). We show the best predictor of long-run changes in life satisfaction is the generosity of the social safety net – more generous, greater happiness – in ten European countries. At the same time, we argue economic growth does not have a meaningful influence on life satisfaction in the long-run.
For my more substantive comment: increasing growth from two to three percent takes 71 years to double income. This is a very long time in my view. I’m not coming from the EA framework. Perhaps the EA community disagrees with me. It matters a great deal however, for both conceptual and empirical reasons.
Fundamentally, you cannot compare doubling one’s income at a point of time (e.g., due to lottery and investment returns or cash transfers) to doubling one’s income in 71 years. 71 is greater than life expectancy in numerous countries. Empirically, the growth-happiness relation depends upon on the time horizon; it gets smaller as the duration increases. We discuss this in the paper conceptually and in reference to the two data sets we use. The longer period in the WVS/EVS data results in lower growth- subjective well-relations. For further support, see Bartolini S, Sarracino F (2014) Happy for how long? How social capital and economic growth relate to happiness over time. Ecol Econ 108:242–256. https://doi.org/10.1016/j.ecolecon.2014. 10.004.
Your replication / robustness tests are not so surprising. As you point out, our results include larger coefficient estimates using different specifications, yet we still argue they are not economically significant, implying we would argue your alternative results are still too small to prioritize growth. Here's the quote: “Based on the largest magnitude across all estimations [larger than what you estimate using 2020 or excluding India], it would still take 100 years for a one percentage point increase in the growth rate to raise happiness by one point.”
To your point, however, even a small increase in subjective well-being for a large number of people is meaningful, but we’re talking about a long time to achieve even these small changes. I’m reasonably assured you can find much more effective policies for short-run gains. See Table 1 of P. Frijters, A. E. Clark, C. Krekel, R. Layard, A happy choice: Wellbeing as the goal of government. Behav. Public Policy, 1–40 (2020).
This table inspired a similar one used by the U.K. government in the Green Book. See:
MacLennan, S., Stead, I., 2021a. Wellbeing Guidance for Appraisal: Supplementary Green Book Guidance, His Majesty’s Treasury: Social Impact Task Force.
MacLennan, S., Stead, I., 2021b. Wellbeing discussion paper: monetisation of life satisfaction effect sizes: A review of approaches and proposed approach, His Majesty’s Treasury: Social Impacts Task Force.
Your robustness test results do not overturn our results; they fall within the range we estimate and only apply to one data set, indeed the one that is based on a shorter period, which is less preferred for reasons explained in the text and implied by the Bartolini Sarracino paper referenced above.
We need more research on wellbeing. Increasing consumption does not necessarily increase wellbeing, especially in highly developed countries.
Perhaps you can explain to me how the GiveWell team determined the “Value assigned to increasing ln(consumption) by one unit for one person for one year” and why this is used in determining the value of subjective well-being benefits (cf. the value: https://docs.google.com/spreadsheets/d/1lTX-qNY1cSo-L3yZCNzMbzIM1kqWC1vSEhbyFAYr6E0/edit#gid=1362437801, which is used in this calculation: https://docs.google.com/spreadsheets/d/1aDUPvizGsgT6rLtIf8RkT8LNTmZyXjlXa7Kddc-UeWM/edit#gid=135302151)?
See instead the MacLennan references above to see a derivation of the monetary value of a life satisfaction point per year.
Unfortunately, I have not had time to go through the comments, and will be slow to respond due to family concerns. I'll do my best to respond and keep up with future posts. Thanks for the lively discussion. I wish we could do it in person.
Lastly, you all probably know the Easterlin Paradox has come under fire for years upon years and in different fields. See his article Easterlin RA (2017) Paradox lost? Rev Behav Econ 4:311–339. https://doi.org/10.1561/105. 00000068. You can also find the working paper version for free on google scholar.
Thanks so much for taking the time to engage in this discussion! I am going to try to reply to where we have interesting areas of disagreement, and to number the points for easier response.
Thank you for sending this. It’s encouraging that we may have levers to move that have larger impacts than economic growth. It definitely updates me away from believing the results of the social safety net regression I outline in my post (although as I mentioned in the post, those results were never that compelling). I used OurWordInData’s “Adequacy of Social Safety Net Programs”. There were only 30 countries, and they were mostly LMICs, so I am not surprised that the results differ from yours. I would be curious what you think of that dataset, and whether the data you use looks like it avoids some of the noise in mine. I would definitely love to see more analysis on this with bigger datasets than both of ours’ if there are any ways to create them. I wonder if the implication might be something like: large social safety nets are effective in European states which have a lot of state capacity to deliver services, and less effective in the LMICs in my dataset.
I think this is an interesting point. If we believe in hedonic adaptation, then we would expect the results of cash transfer RCTs to be much higher than the results over 14 or 40 years like in the two datasets you use in your paper. So the fact that the implied impacts seem to be very similar seems to be (very weak) evidence against adaptation in this context? Am I right in thinking that the results in your two sets of regression implicitly factor in adaptation, since those countries became wealthier slowly? If so, I think we should be comfortable applying the results with 14-40 years (gallup-wvs/evs) of adaptation factored in, to an estimate that looks at benefits spanning from 1-40 years for Ethiopia?
But those coefficients seem to be close to what we would expect from the cross-sectional data? If that is the case, are you suggesting that even if the Easterlin paradox turned out to not hold, we would not update towards thinking more of economic growth? That would imply that a low income country could increase their life satisfaction from around 4 to around 6 if they could figure out a way to enable the kind of catch-up growth that some East-Asian countries have managed.
Thank you for sending this. Reducing fear of violent crime stands out as especially promising to me as a potential intervention. However, it does look like doubling income is still one of the larger results here, and is not obviously harder to achieve than some of the other large-effect interventions. I definitely hope that there are more tractable interventions than boosting growth that we can find. Also, even if we don’t, I think we can probably find ways to do a lot of good by just saving lives, rather than boosting well-being.
I agree. I only meant to try a couple of easy alternative specifications to see how sensitive the results are to them. The Gallup World Poll Data had more countries and was easier to download so I just decided to look at that dataset. If my results are correct, they are not meant to invalidate the Easterlin Paradox. I just think we should be aware that it seems sensitive to specification (even after accepting the exclusion of transition economies, and countries with less than 12 years of data).
GiveWell assigns one unit to an income doubling, so boosting ln(consumption) by one unit is simply =1/ln(2). They then try to estimate the value of saving a life relative to an income doubling by looking at surveys of recipients, Global Burden of Disease estimates, value of statistical life approaches, internal surveys, and other sources. For the purposes of my estimation, you wouldn’t need to accept any of their assumptions except for the fact that it is difficult to find ways to help people that is more than ten times more cost-effective than simply giving cash to the very poorest people in the world.
Thanks again for the interesting exchange.
Hi Vadim, please see my response to your points below. Even if we don't come to agreement, I appreciate your intentions. I appreciate anyone who wants to make the world a better place, and especially those who are actually trying to do something. I operate mostly from the ivory tower.
1. Thank you for sending this. It’s encouraging that we may have levers to move that have larger impacts than economic growth. It definitely updates me away from believing the results of the social safety net regression I outline in my post (although as I mentioned in the post, those results were never that compelling). I used OurWordInData’s “Adequacy of Social Safety Net Programs”. There were only 30 countries, and they were mostly LMICs, so I am not surprised that the results differ from yours. I would be curious what you think of that dataset, and whether the data you use looks like it avoids some of the noise in mine. I would definitely love to see more analysis on this with bigger datasets than both of ours’ if there are any ways to create them. I wonder if the implication might be something like: large social safety nets are effective in European states which have a lot of state capacity to deliver services, and less effective in the LMICs in my dataset.
Response: A brief look at the “Adequacy of Social Safety Net Programs” data indicates it is an expenditure measure. The challenge with expenditure measures are that they mechanically increase as people age or the unemployment rate increases. A better indicator is based on the policies themselves, like the indicator in the referenced PNAS paper. There are approximately 30 countries available in that data set now too, but not for the same duration that we wanted to work with. I published a paper on 104 countries using safety net expenditures and controls to account for the mechanical relation mentioned, however, it only provides a cross-sectional relation (https://www.researchgate.net/publication/321948496_Happiness_and_Welfare_State_Policy_Around_the_World). A positive cross-sectional relation exists in each country group, including the less developed.
There are causal studies on the expansion of the safety net, though they are all likely confined to developed countries.
2. I think this is an interesting point. If we believe in hedonic adaptation, then we would expect the results of cash transfer RCTs to be much higher than the results over 14 or 40 years like in the two datasets you use in your paper. So the fact that the implied impacts seem to be very similar seems to be (very weak) evidence against adaptation in this context? Am I right in thinking that the results in your two sets of regression implicitly factor in adaptation, since those countries became wealthier slowly? If so, I think we should be comfortable applying the results with 14-40 years (gallup-wvs/evs) of adaptation factored in, to an estimate that looks at benefits spanning from 1-40 years for Ethiopia?
Response: I don’t agree that the results are similar in size between the RCTs and long-run trend analysis in Easterlin and O’Connor. It takes 71 years of one percent additional GDPpc growth to increase life satisfaction by 0.142 points, over which time there were 32 income doublings. 0.142 points for 32 income doublings is 0.142/32 = 0.004 points per doubling.
However, you are right that the trend analysis does allow for adaptation. We explain why the relationship is smaller in trend analysis than in cross-sectional relations, and this logic could be extended to short run gains. Briefly, in the short run, your reference point hasn’t changed, while it does in the long run. The reference point is set by both your past experience (adaptation) and peers (comparison).
To look at Ethiopia using my results, you should look at interventions that increase growth, e.g., education, innovation, capital investment, trade… I wouldn’t use your conversion as it add confusion, hence our disagreement.
The results of RCTs can be evaluated as they are currently, but we should not assume the results last or scale to the full population. We need longer-term (than the typical) studies of interventions to assess the long-run impacts, and to assess at the population level, there’s a whole science developing on scaling interventions.
3. But those coefficients seem to be close to what we would expect from the cross-sectional data? If that is the case, are you suggesting that even if the Easterlin paradox turned out to not hold, we would not update towards thinking more of economic growth? That would imply that a low income country could increase their life satisfaction from around 4 to around 6 if they could figure out a way to enable the kind of catch-up growth that some East-Asian countries have managed.
Response: I don’t agree that the results are similar in size. See my other response above. There are low-income countries that have similar subjective well-being as high income countries. The Latin American countries, especially Costa Rica, seem to have figured it out. The primary explanation for their success is in their focus on social relations (including family).
4. Thank you for sending this. Reducing fear of violent crime stands out as especially promising to me as a potential intervention. However, it does look like doubling income is still one of the larger results here, and is not obviously harder to achieve than some of the other large-effect interventions. I definitely hope that there are more tractable interventions than boosting growth that we can find. Also, even if we don’t, I think we can probably find ways to do a lot of good by just saving lives, rather than boosting well-being.
Response: Doubling income may be very effective in certain settings. I do not disagree with this, but that’s not the same as increasing long-run growth. Full employment is my go to conceptually though I would need to look more into this to make a more definitive statement. Saving lives surely increases well-being. Self-reported health has one of the strongest relations with SWB, but the relations are prone to significant bias and difficult to estimate. Saving lives also contributes to WELLBYs or happy life years, which are technically the same, but the former is referenced by the UK government.
5. I agree. I only meant to try a couple of easy alternative specifications to see how sensitive the results are to them. The Gallup World Poll Data had more countries and was easier to download so I just decided to look at that dataset. If my results are correct, they are not meant to invalidate the Easterlin Paradox. I just think we should be aware that it seems sensitive to specification (even after accepting the exclusion of transition economies, and countries with less than 12 years of data).
Response: The implications of your narrative would be an invalidation of the Paradox -- saying the cross-sectional result is the same as the long-run time series. However, I disagree with your conversion as mentioned above. Maintaining the interpretation in growth terms, the results are not so sensitive.
Well done for doing this! I think attempted replications or re-examinations of existing work are under-done in EA and wish more were conducted.
Just wanted to comment to say I thought this was very well done, nice work! I agree with Charles that replication work like this seems valuable and under-supplied.
I forgot to add a very important feature. I don't think income doubling is a helpful conversion in this case. In fact, I think it's quite misleading.
Increasing growth by one percent for 71 years costs a lot more than doubling one's income for a year. In the 71st year, the cost is the same, but there are the preceding transfers that were also necessary to increase subjective well-being. In year 70, the cost was nearly a doubling of income.
I estimate there are nearly 32 annual income doublings when you sum them across the 71 years. You get a portion of an income doubling every year, which can be calculated as (1.03/1.02)^n - 1. In the first year (n=1) it costs you 0.01 of an income doubling. In year 70, it costs 0.98 of a doubling. Summing them from n = 1 to n=71 you get 31.9 doublings.
Your estimated impact should then be the coefficient * 71 /32. If we use .002 as the coefficient on growth, that equals .004 - hardly worth it. The same is true for the lager estimated coefficients. Alternatively, you could look at my calculation to see when the costs add up to a the first cumulative annual income doubling. I estimate this happens between year 13 and 14. Let's say 13.5, then 13.5 years * .002 = .027. You get 0.027 subjective well-being points for a cumulative doubling of annual income in 13.5 years. Again, I think this is not worth it.
Essentially, you need to consider the time involved to double income, for the reasons mentioned in my earlier post, and because it simply costs more. I wouldn't compare these results with those of interventions of cross-sectional studies.
Thanks again for the discussion!
I agree that it’s very reasonable to look at the cumulative “cost” in terms of income doublings, rather than just the final number. But I think then you also need to look at the cumulative well-being gains. You don’t just get the life satisfaction gain of the doubling on your 71st year, you also get smaller gains every year before that, just like you do for the costs.
I’ve set up a spreadsheet based on your example of looking at the first 13.5 years to see when one cumulative income doubling has occurred. In that case, on the first year you get .002 life satisfaction points, on the second .004, until the 13.5th when you get .027. When you sum them you get a total of 0.2 life satisfaction points. You get those at a cost of one income doubling. This is actually larger than would be predicted by my approach of multiplying .002 by 71, which would imply 0.142 life satisfaction points. (The reason it’s larger is that when we are looking at time horizons like 13.5 years, the income doublings don’t really benefit that much from compounding yet, so the cost hasn’t grown quickly enough to get to the .142 threshold, which I believe happens closer to the 100 year mark).
Vadim, I don’t agree with your calculation. In the second year you do not get 0.004 more Cantril Ladder points (SWB), you get 0.002. The estimated equation is ∆SWB = ɑ + β*GDPpcGrowth. ∆SWB is the average annual change in SWB. A one percentage point increase in GDP growth is associated with β additional SWB points per year, every year. In your spreadsheet, you multiplied 0.002 by the number of years, assuming a larger increase in SWB per year (i.e., 0.004 in year 2), which is not correct.
The cumulative increase in the Cantril Ladder by year 13.5 is the number of years multiplied by the increase (13.5*0.002 = .027). As before, you get 0.027 subjective well-being points for a cumulative doubling of annual income in 13.5 years.
I guess that's clear, but it might also help to look at SWB in levels.
SWB at time t equals baseline SWB (SWB_0) plus the change in SWB multiplied by t periods in which it changed.
(1) SWBt = SWB_0 + ∆SWB*t
The average annual change in SWB was estimated in Easterlin O’Connor as
(2) ∆SWB = ɑ + β*GDPpcGrowth
Assuming β=0.002, G_0 is baseline growth, and there is no change in growth, we have:
(3) SWBt = SWB_0 + (ɑ + 0.002*G_0)*t
Assuming a change in growth
(4) SWBt = SWB_0 + (ɑ + 0.002*(G_0+∆G))*t
The difference between (3) and (4) gives us the cumulative effect of additional growth at time t, which equals 0.002*(∆G)*t. The average annual change is always 0.002*(∆G).
After 13.5 years, the cumulative increase is 0.002 * 1 *13.5. = 0.027, assuming a one percentage point increase in growth.
“In your spreadsheet, you multiplied 0.002 by the number of years, assuming a larger increase in SWB per year (i.e., 0.004 in year 2), which is not correct.”
I meant the .004 to represent how much happier a person is after two years of faster growth than they would have been counterfactually (if growth had been 1pp lower). Since their annual change in SWB would have been .002 higher, they would have gotten .004 better off by year 2.
In other words, I think your formulas (4)-(3) represent the impact of additional growth (versus the counterfactual) on life satisfaction at time t (SWBt). So using your: 0.002*(∆G)t = .0021*2=.004 happier than the counterfactual. This is only .002 happier than the counterfactual after 1 year, but .004 happier than the counterfactual if there had been no additional growth at all. So since the person was .002 happier in year 1 and .004 happier in year 2, I would consider that a cumulative .006 happier across the two years.
I think for the cumulative life satisfaction gain to be .027, you would have to expect the person in year 13.5 to only be .002 happier than he would have been without the additional growth (that way he would only be .002 happier each year, for a total of .027 life satisfaction points summed across the 13.5 years). But that would imply that our SWB measure wasn’t annualized, and that it shouldn’t matter whether you’ve been growing for one year or 1000, you would still be happier by the same amount?
Perhaps our difference is in how we are using the word cumulative? By cumulative, I mean actually summing across the counterfactual SWB gains in each of the 13.5 years. I think this is the correct thing to look at if we are comparing it to the income gains in each year summed across the 13.5 years. Perhaps by cumulative you meant just the total counterfactual impact on life satisfaction in year 13.5? But then it seems like we need to add the counterfactual impacts at each of the preceding years?
Perhaps one useful intuition pump would be to compress the whole income doubling into 1 year. Lets say annual growth increases by 100pp. Then we counterfactually double income in the first year. The impact on SWB is 100*.002=.2 life satisfaction points. Which is a bit higher than the estimates from cash transfers.
I see the confusion now and introduce a term that should help. Discussed in response to your points below.
“In your spreadsheet, you multiplied 0.002 by the number of years, assuming a larger increase in SWB per year (i.e., 0.004 in year 2), which is not correct.
I meant the .004 to represent how much happier a person is after two years of faster growth than they would have been counterfactually (if growth had been 1pp lower). Since their annual change in SWB would have been .002 higher, they would have gotten .004 better off by year 2.
In other words, I think your formulas (4)-(3) represent the impact of additional growth (versus the counterfactual) on life satisfaction at time t (SWBt). So using your: 0.002*(∆G)t = .0021*2=.004 happier than the counterfactual. This is only .002 happier than the counterfactual after 1 year, but .004 happier than the counterfactual if there had been no additional growth at all. So since the person was .002 happier in year 1 and .004 happier in year 2, I would consider that a cumulative .006 happier across the two years."
Response: We’re discussing different things. You’re discussing SWB points for one year. The U.K. uses the term WELLBYs, well-being points for one year.
So my statement is correct, subjective well-being increases by 0.027 points for a cumulative doubling of annual income in 13.5 years.
Your statement is also correct if we modify it slightly, from, “when you sum them you get a total of 0.2 life satisfaction points”, to “you get a total of 0.2 WELLBYs for a cumulative doubling of annual income in 13.5 years.”
In hopes of clarifying, assume ɑ=0 and SWB_0= 5
Under baseline growth
Year 1: SWB2_1 = 5+.002*2*1 = 5.004
Year2: SWB2_2 = 5+.002*2*2 = 5.008
Year 3: SWB2_3 = 5+.002*2*3 = 5.012
With 3 percent growth
Year 1: SWB3_1 = 5+.002*3*1 = 5.006
Year2: SWB3_2 = 5+.002*3*2 = 5.012
Year 3: SWB3_3 = 5+.002*3*3 = 5.018
By year 3, the difference in SWB is 5.018 – 5.012. In year 13.5 the total increase is 0.027.
Taking the WELLBY approach:
In year three, the total increase in SWB is .006, but people experienced .004 higher SWB for one year in the preceding year and .002 for one year in year one. Each differential lasts one year. Thus the WELLBYs in year 3 is .002+.004 +.006 = .012 WELLBYs. The total accrued WELLBYs in year 13.5 is 0.2.
0.027 SWB points are `permanent’ whereas 0.2 WELLBYs only last a year. Unfortunately, there are few studies that look at WELLBYs. The best resource on WELLBYs was just made open access “A Handbook for Wellbeing Policy-Making: History, Theory, Measurement, Implementation, and Examples” (https://global.oup.com/academic/product/a-handbook-for-wellbeing-policy-making-9780192896803?cc=gb&lang=en&#)
"I think for the cumulative life satisfaction gain to be .027, you would have to expect the person in year 13.5 to only be .002 happier than he would have been without the additional growth (that way he would only be .002 happier each year, for a total of .027 life satisfaction points summed across the 13.5 years). But that would imply that our SWB measure wasn’t annualized, and that it shouldn’t matter whether you’ve been growing for one year or 1000, you would still be happier by the same amount?"
Response: The population in year 13.5 reports .027 greater SWB points after an increase in growth by one percent (see above). SWB increases by .002 points per year. In year 1000, the population would have experienced 1000 years of additional SWB at .002 per year, which is 1000*.002 = 2 points. However, as I discuss above there are differences in each year that you could call WELLBYs.
"Perhaps our difference is in how we are using the word cumulative? By cumulative, I mean actually summing across the counterfactual SWB gains in each of the 13.5 years. I think this is the correct thing to look at if we are comparing it to the income gains in each year summed across the 13.5 years. Perhaps by cumulative you meant just the total counterfactual impact on life satisfaction in year 13.5? But then it seems like we need to add the counterfactual impacts at each of the preceding years?"
Response: see above
"Perhaps one useful intuition pump would be to compress the whole income doubling into 1 year. Lets say annual growth increases by 100pp. Then we counterfactually double income in the first year. The impact on SWB is 100*.002=.2 life satisfaction points. Which is a bit higher than the estimates from cash transfers."
Response: I mostly agree. The calculation is correct, but the estimated relation is based on long run growth rates, not a one time change in GDPpc. We don’t have the “support” from the data to assess your hypothetical. It is plausible that the growth relation is non-linear and diminishes at higher rates, but we do not know for sure, because we do not observe such growth rates. China and India who had the highest sustained growth rates benefited little from growth as far as we can observe (reported in the paper).
Also, it may be plausible to increase GDP pc for one year by 100 percent but not growth trends, which of course last over many years.
I’m not sure about the coefficient on cash transfers, but the cross-country association between GDPpc and life satisfaction is still much higher.
My paper, referenced in an earlier post shows a larger relation: (https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&cad=rja&uact=8&ved=2ahUKEwiK2uqbsNn6AhWOLzQIHdd8B0kQFnoECBgQAQ&url=https%3A%2F%2Fwww.researchgate.net%2Fpublication%2F321948496_Happiness_and_Welfare_State_Policy_Around_the_World&usg=AOvVaw2BX_q9OsuG--hc-yvZdhfX)
and so this does very well known paper: https://pubs.aeaweb.org/doi/pdf/10.1257/jep.22.2.53?utm_source=link_newsv9&utm_campaign=item_182843&utm_medium=copy
Though be careful with the last paper. The author is not distinguishing between time-series and cross-sectional relations.
Thanks again for the response!
Yes, I am definitely talking about WELLBYs. I meant to say that there are two ways of looking at both income and SWB, a level at a point in time, and the sum of the levels per year (we can think of those as the area under the curve plotted across time). We can call the summed versions INCYs and WELLBYs, and the point in time estimates Income and SWB. So I think in year 13.5, we can say that we get .2 WELLBYs for 1 INCY. Or alternatively, we can say that we get .027 SWBs for 14% Income gain. I don't think that we should be comparing SWBs (a point in time estimate) to INCYs (a summation estimate).
To illustrate I’ll try to go back to the example of boosting Ethiopia’s growth by 1pp, using your coefficient of 0.002. For simplicity, let’s say that Ethiopia starts with a per capita GDP of $1000, a SWB of 4, and a real growth rate of 0%. It seems like we agree that “The population in year 13.5 reports .027 greater SWB points after an increase in growth by one percent.” So if we boost growth to 1% I think we agree that in year 71 Ethiopia would have a per capita GDP of $2000 (versus the counterfactual $1000) and a SWB = 4 + 71*.002=4.14.
Now to address our discussion on (3) in the below thread, you say: "As you point out, our results include larger coefficient estimates using different specifications, yet we still argue they are not economically significant," and then in response to my comment that "those coefficients seem to be close to what we would expect from the cross-sectional data," you comment "I don’t agree that the results are similar in size."
Let’s assume we accept the coefficient from your regression in table 3, column 5: 0.007. That would imply that in year 71 Ethiopia would have roughly twice the GDP than it would have had counterfactually (compared to the 0% growth world), and a SWB = 4+71*.007 = 4.5. This is 0.5 points higher than the counterfactual.
Now let's imagine that in the cross section regression Ethiopia and country X are both exactly on our regression line. Ethiopia is at $1000 and SWB of 4, country X is at $2000 and SWP of 4.5 (That is roughly where the cross sectional regression lines fall as I argue in my post, and as you can see from the graph I include). If there were no Easterlin Paradox, we would expect that if Ethiopia gradually got to $2000 GDP, it would move up the regression line to where country X currently is. But it seems like that is exactly what the .007 regression coefficient implies in the preceding paragraph? If so, is this at odds with your response on discussion (3) in the below thread?
Alternatively, don’t the coefficients from Sacks, Stevenson, and Wolfers 2012 roughly correspond to the larger coefficient estimates in your regressions (since both include 10 year short-term fluctuations)? So if Sacks et. al. convincingly reran their analysis to focus on the same countries and longer time series that you use, and got the same coefficients they did in their paper, would that not update us towards thinking that longitudinal and cross-sectional results might be similar?
I think we could also use a similar argument about the Ethiopian counterfactual SWB = 4 + 71*.002=4.14 to argue that it matches the cash transfer results that I cite in my post.
Vadim, discussing with you will cause me to be more explicit about the time involved in future writing. Thank you. As I first argued, 71 years is a long time, which cross-sectional results do not consider. I respond more completely below.
“Yes, I am definitely talking about WELLBYs. I meant to say that there are two ways of looking at both income and SWB, a level at a point in time, and the sum of the levels per year (we can think of those as the area under the curve plotted across time). We can call the summed versions INCYs and WELLBYs, and the point in time estimates Income and SWB. So I think in year 13.5, we can say that we get .2 WELLBYs for 1 INCY. Or alternatively, we can say that we get .027 SWBs for 14% Income gain. I don't think that we should be comparing SWBs (a point in time estimate) to INCYs (a summation estimate).”
Response I agree with part, in year 13.5 we get .2 WELLBYs for 1 INCY (when INCY equals an income doubling),
and adjusted this statement slightly, 0.027 SWB points for a 14% increase in growth for one year.
However, a 14% increase in growth is rarely observed and never sustained. .002 does not apply to such changes.
"To illustrate I’ll try to go back to the example of boosting Ethiopia’s growth by 1pp, using your coefficient of 0.002. For simplicity, let’s say that Ethiopia starts with a per capita GDP of $1000, a SWB of 4, and a real growth rate of 0%. It seems like we agree that “The population in year 13.5 reports .027 greater SWB points after an increase in growth by one percent.” So if we boost growth to 1% I think we agree that in year 71 Ethiopia would have a per capita GDP of $2000 (versus the counterfactual $1000) and a SWB = 4 + 71*.002=4.14."
Agreed
"Now to address our discussion on (3) in the below thread, you say: "As you point out, our results include larger coefficient estimates using different specifications, yet we still argue they are not economically significant," and then in response to my comment that "those coefficients seem to be close to what we would expect from the cross-sectional data," you comment "I don’t agree that the results are similar in size."
Let’s assume we accept the coefficient from your regression in table 3, column 5: 0.007. That would imply that in year 71 Ethiopia would have roughly twice the GDP than it would have had counterfactually (compared to the 0% growth world), and a SWB = 4+71*.007 = 4.5. This is 0.5 points higher than the counterfactual."
Agreed with the math, however, the coefficient is wrong. You should add the negative coefficient on the interaction term to get the correct relationship 0.007 - 0.005. The largest relationship applies in the transition countries 0.007 + 0.003, but as argued in the paper, they are exceptional cases. And, the WVS/EVS results show smaller coefficients.
"Now let's imagine that in the cross section regression Ethiopia and country X are both exactly on our regression line. Ethiopia is at $1000 and SWB of 4, country X is at $2000 and SWP of 4.5 (That is roughly where the cross sectional regression lines fall as I argue in my post, and as you can see from the graph I include). If there were no Easterlin Paradox, we would expect that if Ethiopia gradually got to $2000 GDP, it would move up the regression line to where country X currently is. But it seems like that is exactly what the .007 regression coefficient implies in the preceding paragraph? If so, is this at odds with your response on discussion (3) in the below thread?"
Although the math is correct (assuming 0.007), it took 71 years to achieve the change in SWB, whereas the cross-sectional results do not consider the time involved. As mentioned before 71 years is greater than life expectancy in many countries, and as the WVS/EVS results show, the coefficients are smaller in longer time series.
The coefficient estimates of .002 or .007 apply to long-run sustained growth after accounting for adaptation and social comparison. If you were to double the income of Ethiopians in one year, neither coefficient would apply. We are not sure what applies. Short run growth typically has a larger relationship, the effect of which diminishes over time, possibly to zero, and the benefits of cash transfers do not accrue to the population as a whole.
I don’t think you want to apply our results to what you’re evaluating, especially considering we are talking about the Gallup results and ignoring the EVS/WVS results. They are preferred for long-run periods (still fare less than 71 years) and they reveal smaller, even negative growth relations.
We should be looking at long run outcomes of interventions and then assessing them at scale. It’s possible that many people on the lower end of the income distribution benefit greatly – indeed many economists, even happiness ones, believe this in their bones. We just need more evidence at scale.
"Alternatively, don’t the coefficients from Sacks, Stevenson, and Wolfers 2012 roughly correspond to the larger coefficient estimates in your regressions (since both include 10 year short-term fluctuations)? So if Sacks et. al. convincingly reran their analysis to focus on the same countries and longer time series that you use, and got the same coefficients they did in their paper, would that not update us towards thinking that longitudinal and cross-sectional results might be similar?"
Honestly, I haven’t read the SSW paper in quite some time, in part because of what you reference here, they shorten the length of the time-series and also because they leave out data that was available to them at the time.
My disagreement about the TS and CS studies is the time involved as mentioned above. The CS studies make it seem like we could magically double income and ignore the time involved. Even if the coefficients are the same, the implications are not. Discussing with you brought this to my attention, and I will discuss it more explicitly in future writing.
"I think we could also use a similar argument about the Ethiopian counterfactual SWB = 4 + 71*.002=4.14 to argue that it matches the cash transfer results that I cite in my post."
See discussion above about time. I simply don’t think my results apply to what you’re assessing.
If I understand correctly, it sounds like we now agree on the math of my post, and on my arguments around which coefficients from cross-sectional vs longitudinal regressions seem to match? But I think we still disagree about whether the impacts of a gradual increase in gdp across time should be compared to cross-sectional differences?
My first thought on our disagreement is that an income doubling is a fairly arbitrary metric. I think it would be equally reasonable to zoom in on the cross sectional graph, and look at the impact of a 1% increase in income. We can imagine country Y on the cross-section graph which lies a little higher than Ethiopia on the regression line in my post. This country would have $1010 per capital GDP and a SWB of 4+1*.007=4.007, versus Ethiopia at $1000 and 4. If we compare this to what we would expect from a .007 coefficient in one of your alternative regressions, it looks like it’s exactly what we would expect from one year of 1% growth vs the counterfactual for Ethiopia? In this case we don’t need to worry about the amount of time it takes to double income, and TS and CS become more intuitively comparable?
My second thought is that if we assume that TS results are not comparable to CS results because they take a long time, wouldn’t that make the existence of the Easterlin Paradox irrelevant for making any judgements about the world? Isn’t the Easterlin Paradox a paradox precisely because we expect the coefficients to match between CS and TS, but they don’t seem to in some specifications?
“we are talking about the Gallup results and ignoring the EVS/WVS results. They are preferred for long-run periods.”
Agreed. I haven’t looked at the EVS/WVS results at all, so there is a good chance that they are less sensitive to the kinds of alternative specifications I tried for the Gallup results.
“It’s possible that many people on the lower end of the income distribution benefit greatly – indeed many economists, even happiness ones, believe this in their bones. We just need more evidence at scale.”
I share the same intuition, and find this an interesting area for further exploration. I would be curious to hear your thoughts on why the “Growth X LDC” coefficients in all of your regressions are negative (which is a surprise to me). This seems to imply that people lower down the income distribution are actually benefiting less from % income increases? Re-running your regressions on just the less-developed countries in your Gallup dataset, I also get smaller coefficients than those for the whole dataset.
“If I understand correctly, it sounds like we now agree on the math of my post, and on my arguments around which coefficients from cross-sectional vs longitudinal regressions seem to match? But I think we still disagree about whether the impacts of a gradual increase in gdp across time should be compared to cross-sectional differences?”
Response: Not quite, I agree with some of the calculations you did in the last post, but not with the overall post and conclusions. The quickest justification for this response is that the EVS/WVS coefficients are smaller and even negative for certain country groups. There’s also the statistical significance to consider, which we have not discussed. There is a large amount of uncertainty in the estimates, and while they could be larger, they could also be zero. But regardless of coefficient, yes, we disagree about the implications of time-series (TS) and cross-sectional (CS) differences.
"My first thought on our disagreement is that an income doubling is a fairly arbitrary metric. I think it would be equally reasonable to zoom in on the cross sectional graph, and look at the impact of a 1% increase in income. We can imagine country Y on the cross-section graph which lies a little higher than Ethiopia on the regression line in my post. This country would have $1010 per capital GDP and a SWB of 4+1*.007=4.007, versus Ethiopia at $1000 and 4. If we compare this to what we would expect from a .007 coefficient in one of your alternative regressions, it looks like it’s exactly what we would expect from one year of 1% growth vs the counterfactual for Ethiopia? In this case we don’t need to worry about the amount of time it takes to double income, and TS and CS become more intuitively comparable?"
Response: You’re right that in that case we do not need to worry about the time involved, but what you’re pointing out is how small the relationship actually is in the cross-section. From the figure, the cross-sectional relationship is: y = -2.955 + 0.342*ln(x). Then a 1 percent increase in income is related to an increase in SWB of approximately 0.342*0.01 = 0.003, which of course is actually smaller than the 0.007 coefficient (note the previous post, 0.007 applies to developed not less developed countries. Also, it is statistically insignificant and could also be zero).
"My second thought is that if we assume that TS results are not comparable to CS results because they take a long time, wouldn’t that make the existence of the Easterlin Paradox irrelevant for making any judgements about the world? Isn’t the Easterlin Paradox a paradox precisely because we expect the coefficients to match between CS and TS, but they don’t seem to in some specifications?"
Response: You’re right that the Paradox is about the contrast between the two types of results. However, it’s not just whether the coefficients match. The CS results are statistically significant and the TS results are generally not statistically significant. A second aspect is that the TS results, even if statistically significant, make it clear how long it would take for SWB to increase. The period necessary is not clear in CS results, which makes it look like the CS results are much larger than the TS results. Your calculation above suggests that the CS results are actually quite small too, or that we need larger changes in income to have meaningful changes in SWB, which as the TS results point out, will take a long time. Another aspect, the Paradox is about the contrast, but the surprising result is how small the TS relation is. Whether there's a contrast or not, this relation is important for thinking about the world.
“we are talking about the Gallup results and ignoring the EVS/WVS results. They are preferred for long-run periods.”
Agreed. I haven’t looked at the EVS/WVS results at all, so there is a good chance that they are less sensitive to the kinds of alternative specifications I tried for the Gallup results."
Response: the sensitivity isn’t too important, because the relationships are all small. As stated above, even the CS results are quite small, or we need larger changes in income to have meaningful changes in SWB, which as the TS results point out, will take a long time.
“It’s possible that many people on the lower end of the income distribution benefit greatly – indeed many economists, even happiness ones, believe this in their bones. We just need more evidence at scale.”
"I share the same intuition, and find this an interesting area for further exploration. I would be curious to hear your thoughts on why the “Growth X LDC” coefficients in all of your regressions are negative (which is a surprise to me). This seems to imply that people lower down the income distribution are actually benefiting less from % income increases? Re-running your regressions on just the less-developed countries in your Gallup dataset, I also get smaller coefficients than those for the whole dataset."
Response: The Growth X LDC coefficient applies to lower income countries not strictly lower income people. The distinction is important because we can expect the mechanisms to be different. The impacts of income within a country are absolute and relative, due to social comparison as well as cost of living. Recall that poverty is usually defined in relative terms, i.e., as 60% of the median. While at the country level, I expect income to operate more in absolute terms. It’s not clear to me why growth does not help more in these countries.
What I can suggest are two papers that discuss the quality of growth: (1) https://www.sciencedirect.com/science/article/abs/pii/S0305750X17300049
(2) Helliwell, J. (2016). Life satisfaction and quality of development. In Bartolini, S., Bilancini, E., Bruni, L., and Porta, P., editors, Policies for Happiness, chapter 7, page 149. Oxford University Press.
There should be others too. For partial explanations (off the top of my head), think income inequality, quality of jobs (security), corruption, work hours, and materialism.
I'm curating this post — thank you so much for writing it.
I agree with other commenters that replication is extremely precious, and I think this post chooses an excellent work to replicate — something that is quite influential for discussions about whether we should prioritize economic growth or more direct types of global health and wellbeing interventions. (Here's a pretty recent related piece by Lant Pritchett.) I also really appreciate that the conclusion about economic growth seems to rely on three very different but independently strong arguments (straightforward estimation of impact given Easterlin's values, noting that the conclusions are very sensitive to small tweaks in the methodology, and suggesting that GDP interventions might be a better approach to improving wellbeing even if Easterlin's interpretations are accurate).
Re: the discussion on tractability, I want to note that most problems [seem to] fall within a 100x tractability range (assuming that effort on the problems has ~logarithmic returns, which seems very roughly reasonable for, say, research on economic growth or better global health interventions). ("For a problem to be 10x less tractable than the baseline, it would have to take 10 more doublings (1000x the resources) to solve an expected 10% of the problem. Most problems that can be solved in theory are at least as tractable as this; I think with 1000x the resources, humanity could have way better than 10% chance of starting a Mars colony, solving the Riemann hypothesis, and doing other really difficult things.") If I'm interpreting things correctly, I think this means a more plausible reason other interventions might be more impactful is if they're much more neglected (rather than much more tractable). Alternatively, we should simply not expect them to be more impactful. (Disclaimer: I read the tractability post quite a while back, didn't follow the links in this post, and didn't try very hard to understand the parts that I didn't understand after a first read. I also don't have any proper expertise in economics, so I might be getting things significantly wrong. I'm also writing quickly while tired.)
Finally, for those who like Our World in Data charts (and for those who'd appreciate a reference on what we should expect in terms of the relationship between GDP and measures of happiness) — here's a chart showing self-reported life satisfaction vs GDP per capita in different countries (note that this is different from Easterlin's approach for the paradox, which looks at differences in GDP and happiness within countries over time):
Thanks so much for the kind words.
I think the question of the the plausible range for tractability is an interesting one. I suspect that most global health interventions seriously considered by EA fall within a 100x range. But I would guess that the reason this is true is that the only interventions with enough evidence are already in the process of solving more than 0.5% of the problem. At the other end of the spectrum, I suspect intervention trying to influence the very long term trajectory of human culture might fall into a range that spans at least 6 orders of magnitude. There are probably plenty of interventions we could consider that we should expect to have much less than a one in a million chance of solving 10% of the problem. Because there is little evidence and feedback for what would work in this context, we should not expect most things we consider to have a non-tiny chance of working.
I am also a little skeptical of how much information we get out of neglectedness when working with these sorts of problems. I think something being neglected might often be a sign that experts in the space don't consider the approach plausible, or that some experts have tried it and given up on it. If that is the case, then that effect may swamp the diminishing marginal returns we might expect. Additionally, diminishing marginal returns might not be as common in fields where it's not obvious what the next good thing to do is (because there are poor feedback mechanisms).
Oh, and thanks for the transparency. I appreciate being able to follow the calculations. Great practice.
Generally this discussion, even within EA circles, is much too short-termist.
Most people in EA don’t discount the future much, if at all. This means they will care about timescales of thousands or millions of years. The compounding nature of economic growth means that increased growth could result in people in the mid-far future becoming much richer than they otherwise would have been. So even a small impact of a typical annual rate of economic growth on happiness can mean a lot of extra happiness over a long time frame. This impact, you rightly imply, may not be able to be matched by other interventions.
The best counterarguments to this are:
For the record I still think from a longtermist point of view we shouldn’t be thinking of happiness at all, and instead about navigating between lock-in scenarios a la MacAskill/Ord. When/if we reach existential security we can then think about happiness.
Thanks so much for the thoughtful reply.
First let me say that I agree with you that the impacts of economic growth are likely to be much higher than those implied by the conservative 40 years I chose to consider in order to present something like a lower bound on impacts.
But then let me follow you in presenting two additional counter-arguments to the more long-termist framing:
It is possible that we should expect any growth our interventions generate to be canceled by a dip at some point in the future. I don’t know much about the topic, but I believe the economics literature leans towards suggesting this is generally not the case. However, it seems plausible that an intervention that drove a country to operate above its productive capacity would likely be canceled in the future.
The kinds of interventions I imagine to be effective at stimulating growth would likely be interventions to help a poorer country catch up with the productive frontier. In those cases, an intervention would potentially simply help a country get to that frontier faster, and after that growth would be slower than it would otherwise have been. I still think we would get far more than 40 years of benefit out of these kinds of interventions, but they would not propagate into the long-term.
I am also interested in your comment about reaching diminishing marginal utility of GDP in more developed countries today. I ran a quick regression of the developed countries in Easterlin’s dataset, and the coefficient on GDP growth actually increases. This implies that an income doubling actually matters more in rich countries today than it does for poorer countries. I believe I’ve seen economists who have looked at the data noting the same. This result is surprising to me, so I would be interested for your thoughts.
Lastly, I share the intuition that we should not worry as much about happiness as existential security. This may be another argument against thinking too much about stimulating the kind of growth that would compound into the long-term. That kind of growth would likely be frontier growth, potentially increasing existential risk as we develop new technologies.
I don't see how your two counterarguments are arguments against a longtermist framing. Rather they seem to be arguments against the benefits of economic growth if one has accepted a longtermist framing (maybe this is what you meant?). If you're saying the benefits of economic growth don't stretch into the long-term then that acts against economic growth, although for the record I'm not convinced on the truth of claim (1).
How long can this continue? That's what I wonder. When we're all rich enough to have a pretty nice set of material possessions, is more growth going to continue to boost our happiness? Certainly in my own life I don't want more material goods - I want better relationships and more meaning. Also there have been criticisms of using SWB data in low-income settings - see my comment here.
For the record, some have argued that technological progress and economic growth can lower existential risk. This is because we can develop technologies that can allow us to reduce risks, as well as becoming richer making us more concerned with safety. See here and also Will MacAskill's new book What We Owe the Future which discusses the risks of stagnation.
Yep, you are correct about what I meant by a longtermist framing. I meant to say that arguing for economic growth based on its long term effects is a little controversial. I am only 60% certain that economic growth is good after 40 years in the future, but I am more like 80% certain that it's good in the 40 year time-frame.
On how long can wealthy countries continue to benefit from growth: Looking at individual life satisfaction data, it looks like income doublings may continue to steadily increase life satisfaction at incomes that are at least 8x today's United States median income. Considering that median wages in developed countries have been growing pretty slowly the past few decades, it seems likely that we have another few centuries of growth in the richest countries before we have to start worrying about reaching a limit. More speculatively, I am also not sure that we ever have to reach a limit. It seems like there should be biological limits to how happy you can feel in the moment, but it might be possible to be 10x as satisfied with your life as you are right now. I agree with you that relationships and meaning are more likely to get you there than material goods. But richer people in the US seem to participate in communities more and have better relationships, and I believe people in richer countries broadly have more close relationships than people in poorer ones.
On frontier growth lowering existential risk: I definitely think it's plausible. But technological progress so far has only seemed to consistently increase existential risk. I think there is a large burden of proof on the claim that going forward things will be different. I think the EA community should be especially suspicious of such claims considering how much we discuss mechanisms of how further developments in synthetic biology or AI could pose an existential risk.
I don't think this is true:
In the latest EA Survey (from 2020, admittedly), global poverty (not a longtermist cause) still ranked as the top cause among respondents. I personally find analyses that compare economic growth to global health interventions in terms of short-term impact valuable for people prioritizing within the global poverty cause area.
Prioritising global poverty doesn't necessarily mean you discount the future. You might prioritise it because you don't think the leading longtermist interventions are tractable or for other reasons e.g. population ethics.
I personally don't find just considering short-term impact to be helpful but appreciate others disagree.
Do you expect a marginal increase in growth now to affect things much past the arrival of AGI? I would guess it wouldn't.
To be clear, I'm most interested in the far future with this question. I can still imagine growth being slow for some time with AGI (although I'm not sure), but it would still lead to a kind of economic transition that isn't very sensitive to current capital and resource levels and composition, because we'll have much better ways to acquire capital and resources with AGI, including also the capital and resources most useful to AGI. Almost all of the impact on the far future of economic growth seems like it would be through how it affects AGI or other lock-ins like extinction:
I agree that the impact would not go far beyond the arrival of AGI. That was part of the reason I chose a 40 year time frame, to make the argument less controversial for people who think the arrival of AGI is very probable this century.
However, I think the arrival of AGI this century is just too extreme of an outcome relative to all of our history to have more than a 30% confidence in. So I still think over 70% of the long-term value of growth (positive or negative) would be realized in expectation.
In response to your three scenarios for the impacts of growth on AGI, I think growth in the United States or China is most likely to lead to (1). However, the kind of growth I would advocate for, in low income countries, would be more (3). Although there is a good chance that the benefits of AGI will be captured by developed nations, and low income countries will benefit from any growth they can get now even in a world of AGI.
Another counterargument to this is that a small impact on the annual rate of growth could be essentially noise over the long term with no long term impact, rather than necessarily compounding for thousands or millions of years.
I really don't understand the results of point 1. I guess I miss something.
Easterlin’s estimates include many countries, including a significant number of economically strong countries, right? And cash transfers are directed to the very poor, aren't they? If so, I really don't understand how the increase in happiness due to cash transfers is not much higher than that of Easterlin’s estimates (or at least significantly higher if only a small fraction of the countries included are rich). Isn't it well established that the effect of wealth in happiness is much stronger for poorer people? What am I missing?
There are two different things you could mean by "effect of wealth in happiness is much stronger for poorer people":
Giving $1000 to a family in Kenya brings them much more life satisfaction than giving $1000 to a family in the United States: This is uncontroversial. Since Easterlin and O'Connor's regressions look at the impact of percent change in GDP, they are assuming a logarithmic utility function. Therefore, a $1000 increase would represent something like a 100% GDP increase, while it would only represent something like 1.5% in the US. So the impact on happiness in Kenya would be much higher to be consistent with the regression.
Utility functions aren't actually logarithmic. A 1% increase in income should bring a lot of happiness in Kenya, but almost none in the United States, because the United States has maxed out: I think Easterlin, O'Connor and some other economists believe this. Others don't. I ran a quick regression of my own on Easterlin's data, and it suggests that a 1% increase in income for developed countries actually increases happiness more than a 1% increase in LMICs. So that would lead us to expect that the impact from cash transfers might actually be a bit smaller than the results of Easterlin-style regression.
Thanks for the answer. I was referring to 2. I thought it was something we'll established. But I think I was so convinced of it because I did not think much about and I probably conflated it with 1 as well.
You conclude that there is a degree of Easterlin Paradox - that happiness increases less with growth over time than would be expected from how happiness increases with income within a country and how it increases with income levels between countries.
To what extent do you think that the remaining Easterlin effect is due to status levels being an important aspect of happiness so we don’t benefit much if our neighbours get richer with us? Or do respondents adjust life satisfaction scales as life expectations advance with incomes over time, so that happiness improves but is not measured?
Great question. The difference between the cross-sectional (CS) positive relation between GDP pc and life satisfaction and the nill time-series (TS) relation is best explained by social comparison. See the article for details.
However, people also surely adjust their expectations over time, Bernard Van Praag used the term preference drift to refer to the phenomenon described (https://www.nowpublishers.com/article/DownloadSummary/MIC-026), and psychologists use the term hedonic treadmill. This is important, but not enough to explain the difference between the CS and TS results. There are other explanations too, essentially that it is the quality of growth that matters, see (https://www.sciencedirect.com/science/article/abs/pii/S0305750X17300049)
Thank you for your response, and for referencing the two papers.
Thanks for this. It has rocked some of my priors - I don't believe in Easterlin's paradox anymore. On the other hand:
I agree that, by modus tollens, this shows one should be suspicious of Easterlin’s overall argument. But I think that this metric is not the best proxy to measure increase in welfare due to better health. I’d be surprised if lives saved increased average life satisfaction. Even from an individual point of view, and even though most people have a strong preference for surviving and usually see their lives as net positive, I don’t think that avoiding death makes the person much happier quite often people surviving accidents and disease become traumatized or more careful about life).
Also, I’d be astonished if it made this person happier than the population mean – which is required for us to observe an increase in average life satisfaction. I guess the people most likely to die are precisely those who tend to be less “happy” in most metrics (e.g., depressive individuals, or the poor, or people with health conditions…); so one can intuitively conceive of a reduction in average happiness by decreasing some deaths. Thus, unless one adopts some weird position in population ethics (or bites the bullet and becomes a hedonic utilitarian villain willing to let sad people die), I don’t think it’s bad news that your “r-squared of the regression is essentially 0”.
That’s an interesting point. It sounds like you are probably right that we shouldn’t expect better health to improve life satisfaction. I could try to argue that everyone being a little healthier for the first 70 years of their life would mean less unemployment, loneliness and chronic pain, and that those effects would be larger than the ones you bring up. But I don’t think that’s likely.
I also agree with you that the main value of better health is just in averting years of life lost. In fact, I think global health interventions are likely to be better than growth interventions for this reason.
The reason I ran the health regression (as it seems you surmised) was because that was something that people have brought up as something that might be better than gdp growth at boosting happiness, and we have good longitudinal data on it.
Agreed, and I commend you for this.
On the other hand, I'm afraid we might be talking past each other here (though I'm not sure how important this is):
I didn't say that - my fault, I think I wasn't clear enough. I'm pretty sure I would be less satisfied with life if my health was worse, and I think one can extrapolate that for most people - just ask them, or observe how their satisfaction decreases after they get sick, or compare sick and healthy people, etc.
What I said is that my average satisfaction wouldn't increase if my life was saved. And I meant that your regression using "number of years people in a country lose to ill health" is probably a poor proxy for what you're trying to measure (i.e., better health vis-a-vis life satisfaction). This is because your metric health years is probably dominated by averted deaths (especially if one is tracking marginal improvements), and average life satisfaction only measures the welfare of those who are alive - because the dead don't speak.
Take world1: I suddenly die of disease on my 6th birthday, and world2: my life is saved on my 6th birthday. There's no reason to believe that:
(I now realize this might explain why some scholars use increases in mean height to measure the effects of health improvements - because this is likely more robust)
I think we are on the same page here. I was just using "improve life satisfaction" as shorthand for "improve average life satisfaction across the whole population."
Given that the results seem sensitive to arbitrary changes to how you analyse the data, might be worth doing some sort of multiverse analysis : https://www.martinschweinsberg.com/multiverse-analysis-exploring-the-entire-universe-of-analyses/
Second, I feel like there are 2 separate questions being discussed here.
Many of these papers ask the question "have the historic increases in GDP seen throughout the world been associated with increases in happiness?"
What we're actually interested in is "does increasing GDP increase happiness? And under what circumstances?" These are questions of causal inference, and so regression analyses with few to no control variables can be really misleading.
Imagine the following scenario: GDP has increased, which makes people happier, but the way we have achieved higher GDP has been at the cost of rising income inequality, declining leisure time and greater environmental damage. All of these have largely offset the increase in happiness that GDP would otherwise bring. In this scenario, GDP can, * in theory* increase happiness, but only if it's achieved without compromising on other things.