Introduction
This article is a response to the 2018 paper ‘Dissolving the Fermi Paradox’ by Anders Sandberg, Eric Drexler, and Toby Ord. The Fermi Paradox is the apparent contradiction between the great size and age of the universe, which seem to imply a high probability of extra-terrestrial life, and the fact that no extra-terrestrial life has been definitively observed. In their paper, Sandberg et al. use the Drake equation to estimate the expected number of alien civilizations in the Milky Way galaxy and in the observable universe. What differentiates their approach from previous efforts to answer this question is that they do not simply make a point estimate for the number of alien civilizations. Instead, they estimate the uncertainty for each parameter in the Drake equation, and then take random draws from the distribution of each parameter to estimate the distribution for the end result. Using this technique, they find that, although the mean expected number of alien civilizations may be high, there is a large tail of very low expected values, which means that overall the probability of Earth being the only planet to harbour civilization in the Milky Way, and indeed even in the observable universe, is fairly high. On this basis, the authors argue that since it is quite likely given our existing knowledge that no other intelligent alien civilizations exist, the Fermi Paradox is not paradoxical at all, and is therefore dissolved.
In this essay, I will argue that the analysis of Sandberg et al. is flawed in a number of key respects, and as a result the Fermi Paradox remains an open question. Here I briefly list the key problems with the Sandberg et al. paper, before proceeding to discuss each in more detail.
- The method used of multiplying uncertainties of many small numbers, most of which have an upper bound of one, is biased towards yielding a result of a high probability of Earth being unique, while also leading to various dubious results.
- The key result of the paper is driven largely by uncertainty in the parameter fl, which is modeled in an unusual way without clear justification.
- Adoption of slightly different (and I believe more plausible) modelling choices and parameter values yields totally different results, which do not result in the Fermi paradox being dissolved. I illustrate this by re-estimating the Sandberg et al. models using different parameters and modelling assumptions.
Multiplying small numbers
The very nature of the Drake equation, in which seven apparently-independent parameters (four of which are fractions) are multiplied together, means that it has the potential to give very low numbers. Indeed, since the rate of star formation is fairly well-established to be around 1-10, the average longevity of detectable civilizations is ultimately bounded by the age of the universe to around 10 years, and the number of Earth-like planets per star is generally set at one, it follows that the largest possible number detectable civilizations in the Milky Way galaxy is 10^11, or about the same as the number of stars in the galaxy. By contrast, there is no lower bound to any of these numbers, especially the four fractions, which can potentially be set to arbitrarily low non-zero values. The potential for abusing multiplication of fractions to give extremely low numbers is well known. A particularly egregious example of this can be found in the work of Christian apologist Tim McGrew, who estimates the prior probability of having the evidence we do pertaining to the resurrection of Jesus at less than 10^-40, on the basis of multiplying together supposedly independent probabilities of each of Jesus’ disciples separately experiencing a hallucination. The Drake equation does not reach this level of absurdity, but nevertheless I think it is important to bear in mind that the structure of the equation makes it potentially much easier to get very low values than very high values.
This is especially relevant because the methodology adopted by Sandberg et al. involves identifying sources of uncertainty (especially for the parameters fl and fi), and then using any such uncertainty to argue for wider parameter intervals. Wider parameter intervals, however, almost invariably result in higher probabilities for Earth being alone in the Milky Way and the universe. Interestingly, in arguing for the rare Earth hypothesis, Ward and Brownlee explicitly acknowledge this, noting that they “have accumulated a laundry list of potentially low-probability events or conditions necessary for animal life”. Contrary to the intention, such statements reduce my confidence in the method being applied, since it is all too easy to come up with more and more factors that can be multiplied to produce smaller and smaller numbers. This approach can also lead to bizarre consequences. For instance, under this method uncertainties which increase the number of possible avenues by which life may emerge (such as alternative encoding methods), increase our uncertainty about the value of the fl parameter. However, since this parameter is capped at 1, while there is no lower limit to the long tail of very low estimates for fl, in practise this primarily has the effect of reducing the estimated probability of life emerging spontaneously, even though it represents an additional pathway by which this could occur.
There are some further problems with the way the Drake equation is defined, and also the way it is applied in this study. First, it is not clear why it is assumed that life can only exist on planets. It seems just as probable that life could emerge on moons, either of rocky planets or of gas giants, as in the proposal that life may exist in the oceans of Europa. Given this consideration, is seems reasonable to consider the average number of habitable planets and moons per solar system. This would potentially increase the maximal bounds on parameter by one or two orders of magnitude (see Table 1) based on the number of moons in our own solar system (there are ten moons with atmospheres). Second, defining the parameter fl as the fraction of planets that develop life amounts to an implicit assumption that life can emerge at most once in the history of each planet. It seems to me, however, that such an assumption is unwarranted. Presumably life could evolve multiple times on the same planet, perhaps in succession following an intervening extinction event, or perhaps in different regions of the same planet that are inaccessible to each other (for example a planet with disconnected oceans). A similar possibility should also be considered with respect to the parameter fi, the fraction of planets with life that becomes intelligent, as there is no obvious reason why multiple intelligent species cannot evolve on the same planet. This might take the form of such species coexisting, or could involve one species evolving after the previous species became extinct, or even a second species evolving after the first had left the home planet to colonise other planets. Third, the Drake equation does not seem well-suited to incorporate either the seeding of life from one planet to another (which is called panspermia), or of speciation following stellar settlement, both of which would result in large numbers of contactable civilizations even if the emergence of intelligent life on a given planet is very unlikely. These latter scenarios are speculative to be sure, but ignoring these factors would lead to a downward-bias in the estimates of the Drake equation.
Table 1. Parameters used in the Sandberg paper compared to my preferred values.
Symbol | Meaning of parameter | Sandberg et al. | My preferred | Explanation of my preferred |
| The rate of star formation per year | 1 to 100 | 1 to 10 | Based on Robitaille and Whitney, 2010 | |
| The fraction of stars with planets | 0.1 to 1 | 1 | Evidence of abundance of exoplanets, e.g. Cassan et al., 2012 | |
| The number of Earth-like (or otherwise habitable) planets per system with planets | 0.1 to 1 | 0.1 to 100 | Incorporating habitable moons | |
| The fraction of habitable planets with life | -λVt ~ LogN(1,50)
| 0.01 to 1 | See below in text | |
| The fraction of planets with life that becomes intelligent | 0.001 to 1 | 0.0001 to 1 | Based on Sandberg et al., but slightly less optimistic. | |
| The fraction of intelligent civilizations that become detectable/contactable | 0.01 to 1 | 0.1 to 1 | Based on Sandberg et al., but slightly more optimistic. | |
| The average longevity of such detectable civilizations in years |
to
|
to | Based on Sandberg et al., but slightly more optimistic. |
The origin of life
Sandberg et al. model all of the parameters of the Drake equation using log-uniform distributions except for the fl parameter, for which they use a method by which they estimate the rate parameter per unit volume of a given planet undergoing an abiogenesis event per unit time. It is not explained why this method was used for this parameter while all the other parameters were based on values from the cited literature. Indeed, it seems that other parameters could potentially be modelled using similar methods. For example, the development of intelligent life could be modelled as having some probability per extant species per unit of surface area of a planet, or the longevity of a civilization could be modelled as a function of its population and resource availability. Furthermore, the justification for using a log-normal distribution with standard deviation of 50 is unclear. In supplement i, following a discussion of protein folding, the authors assert that “taking LU[λ] > 300 (log uncertainty of λ) as a reference value seems conservative. To claim confidence that LU is less than 300 would be bold, even allowing for a combinatorially large set of alternative AGT (abiotic/genetic transition) paths and outcomes”. However it is unclear how this number was arrived at, or on what basis 300 was chosen instead of any other number. In my view, abstract considerations of protein folding rates are not an appropriate way to estimate the probability of abiogenesis, as early forms of life would have likely relied upon currently unknown mechanisms of catalysis to significantly increase reaction rates.
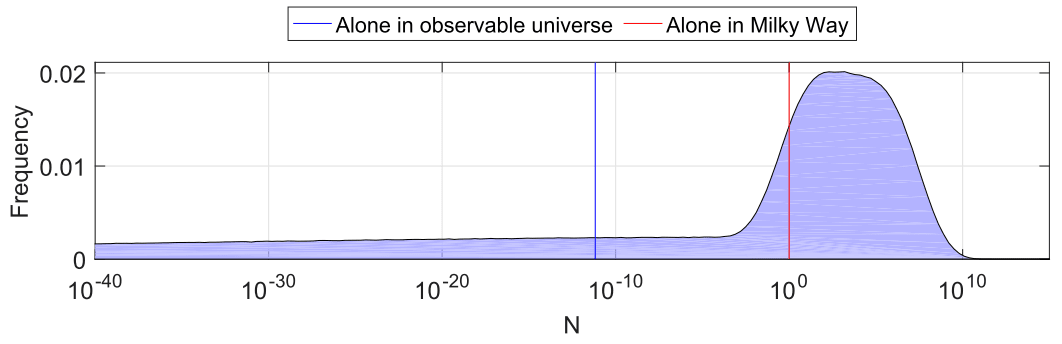
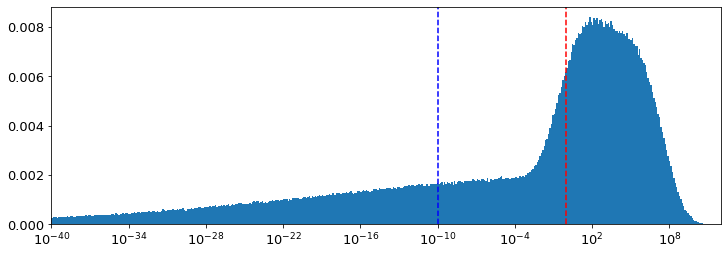
As the authors note, the main result of the paper can be produced by relying entirely on the uncertainty of fl, even while setting all other parameters equal to their most optimistic values (see Table 3). However, the enormous uncertainty in fl is not only sufficient, but also necessary to drive the result. As I show in Table 3, if the fl parameter is modelled in the same way as fi and the other parameters, namely as a log-uniform with an interval determined by the cited literature (which I set to a range of to 1, derived from the cited literature but ignoring a few outliers as discussed in Table 2), the probability of Earth being alone in the universe falls to almost zero. This result illustrates that the main effect reported by Sandberg et al., namely that the Fermi observation is not antecedently very improbable given our current knowledge of parameters in the Drake equation, is entirely dependent on their largely unexplained approach to describing the uncertainty in fl. If it is treated like the other parameters in their equation, the effect vanishes.
Another problem with the method adopted by Sandberg et al concerns some of the very low parameter estimates for fl and fi cited in supplement iii. As I show in Table 2 below, none of the very low estimates for these parameters are based on any scientific considerations. I did not investigate the higher estimates of these parameters, and so cannot claim that these are based on any better evidence than the very low values, but this lack of substance inclines me to be highly distrustful of estimates of fl or fi based on aggregations of expert opinion, since much opinion seems to be informed by little to no actual evidence or modelling. Although Sandberg et al. comment that “there is also a clear bias present towards optimistic, high values since SETI or ETI skeptics typically do not give estimates”, it is not obvious that this is true given the significant number of very low values reported here. Furthermore, four of the six parameters that I was able to check were not reported correctly, either because the stated number did not appear in the original source, or because the number had been misinterpreted to refer to fl or fi when it fact it was an estimate of something else. This further reduces my confidence in the method of estimating the parameters based on existing literature.
Table 2. Summary of the lowest reported literature values of fl and fi.
Year | Source title | Estimate | Explanation | Accurate |
| 1965 | Dimensions and probability of life | This is a combined estimate of the probability of life and intelligent life. It is based on the probability of 'man existing in its present form', based on an ad hoc multiplication of the number of mutations needed to produce modern humans. This is not an estimate of the probability of life or intelligence in general. | Yes | |
| 1980 | Extraterrestrial intelligent beings do not exist | This estimate is actually for a combination of fl, fi, and fc, and is based entirely on the fact that probes from alien probes have not been observed. Hence this cannot be used to compute an estimate of the number of civilizations prior to the Fermi observation. | No | |
| 2012 | How Likely is Extraterrestrial Life? | I can't find this number in the cited text. On page 41, the value 10^-17 is given as the probability of a 120 nucleotide long polymer forming randomly in the lifetime of a single planet, but this is not asserted to be an actual estimate of fl. | No | |
| 2015 | On the history and future of cosmic planet formation | This is not an actual estimate, but just an ‘arbitrarily small value’, based on a set of previous estimates, none of which mention actual numbers. | Yes | |
| 1982 | Atmospheric evolution, the Drake equation, and DNA: sparse life in an infinite universe | I have not been able to find this chapter online, and although I ordered the book it has not yet arrived, so I am not able to assess this estimate. | NA | |
| 2009 | The search for extraterrestrials: intercepting alien signals | This figure is not in the source given; the provided table gives a probability of 10%. Furthermore, the table is provided simply as an illustrative example, not an actual estimate. | No | |
| 2015 | On The History and Future of Cosmic Planet Formation | The number 10^-5 is actually the fraction of habitable planets with communicable civilizations. This value comes from Carl Sagan's 1963 paper, but Sagan is actually referring to the proportion of all stars that have a communicative civilization. Sagan’s actual estimate for fi is 0.1. | No |
An alternative modelling approach
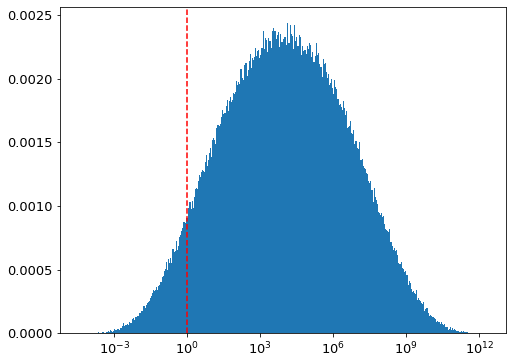
While Sandberg et al. argue that observer selection effects prevent the use of the short time taken for life to emerge on Earth as evidence in favour of a high value for fl, I believe this is mistaken. As Lineweaver and Davis argue, the observer effect that is imposed is that Earth must have existed for long enough to have allowed life to emerge. However, as far as we know it is equally possible that we could have found ourselves on a 9 billion year old Earth instead of a 4.5 billion year old one, had it been the case that life took a lot longer to develop than it actually did. Even with just this modest constraint, Lineweaver and Davis estimate that the 95% confidence interval for the probability of life emerging on planets similar to Earth during the same time period is at least 0.13. On the basis of this argument, as well as other considerations I mentioned previously concerning the possibility of radically different forms of life, I believe it is reasonable to model fl as log-uniform between 0.01 and 1. Incorporating this estimate along with my other preferred parameter values (see Table 2), I estimate at a 6% probability of Earth being alone in the Milky Way, and an effectively 0% chance of Earth being alone in the universe (see Table 3). These estimates were constructed by first attempting to replicate the original results, and then modifying the parameters and modelling assumptions in accordance with the various cases considered in Table 3. While I cannot defend my preferred parameter choices with great confidence, I do believe they are at the very least no less defensible than those used by Sandberg et al. As such my point is that, as has been the case since its invention, the Drake equation tells one more about the person making the estimates than about the probability of alien life. If one believes that alien life is likely to be rare, then low values can be chosen for the parameters, and a low estimate will be produced. Conversely, if one tends to think alien life is likely to be fairly common, large values can be chosen, and therefore a higher estimate produced.
Table 3. Summary of results for key models, with mean and median number of alien civilisations.
Model | Mean | Median | P(N<1) in Milky Way | P(N<1) in Universe |
| Main Sandberg model | 2.70E+07 | 0.32 | 52% | 38% |
| My re-estimate of main Sandberg model | 2.73E+07 | 2.32 | 47% | 26% |
| My re-estimate of main Sandberg with fl like fi | 3.15E+06 | 1 | 50% | 0.004% |
| Sandberg model with uncertainty in fl only | Unknown | Unknown | 41% | 32% |
| My re-estimate of Sandberg model with fl only | 5.12E+11 | 9.17E+11 | 28% | 15% |
| Naive model with literature log-uniform values | 5.07E+03 | 0 | 96% | 51% |
| My preferred model | 3.18e+08 | 9.95E+03 | 6.16% | 0.000% |
Conclusion
In this essay I have argued that the analysis presented by Sandberg et al. concerning the dissolution of the Fermi paradox is multiply flawed. First, the approach of multiplying many parameter intervals with an upper bound at one, but no corresponding lower bound, predisposes the resulting distribution of the number of alien civilisations to exhibit a very long negative tail, which drives the reported result. Second, the method used to estimate the distribution of the parameter fl is insufficiently justified, and the main result of the paper disappears if this parameter is modelled in the same way as the other parameters. Furthermore, the very low estimates of fl and fi reported in the literature review as supporting evidence are mostly misstated from their sources, and are based on vague speculation rather than specific scientific evidence. Third, an alternative modelling approach which incorporates the evidence of the early emergence of life on Earth, and also makes slightly different assumptions regarding the other parameters of the Drake equation, finds a much lower probability that Earth is unique in the Milky Way, and a negligible chance of being alone in the universe. Overall, while Sandberg et al. have made a significant contribution to the study of the Fermi Paradox and the Drake equation by illustrating how computational methods can be used to construct distributions for the probability of various numbers of alien civilisations, I do not believe they have succeeded in showing that the probability of Earth being alone is sufficiently high so as to dissolve the Fermi paradox. Indeed, I present two different set of parameters which yield a negligible probability of Earth being alone in the universe, and hence insomuch as the estimated number of alien civilisations depends crucially on the chosen modelling assumptions, the Fermi Paradox remains very much an open question.
Note: readers interested in experimenting with their own choice of parameters or alternative modelling assumptions are invited to download the jupyter notebook here.
References
Behroozi, P., & Peeples, M. S. (2015). On the history and future of cosmic planet formation. Monthly Notices of the Royal Astronomical Society, 454(2), 1811-1817.
Blum, H. F. (1965). Dimensions and probability of life. Nature, 206(4980), 131-132.
Carter, B. (1983). The anthropic principle and its implications for biological evolution. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 310(1512), 347-363.
Halley, J. W. (2012). How Likely is Extraterrestrial Life? : Springer Science & Business Media.
Lineweaver, C. H., & Davis, T. M. (2002). Does the rapid appearance of life on Earth suggest that life is common in the universe? Astrobiology, 2(3), 293-304.
McGrew, T., & McGrew, L. (2009). The argument from miracles: A cumulative case for the resurrection of Jesus of Nazareth. The Blackwell companion to natural theology, 593-662.
Robitaille, T. P., & Whitney, B. A. (2010). The present-day star formation rate of the Milky Way determined from Spitzer-detected young stellar objects. The Astrophysical Journal Letters, 710(1), L11.
Ross, M. (2009). The search for extraterrestrials: intercepting alien signals: Springer Science & Business Media.
Sagan, C. (1963). Direct contact among galactic civilizations by relativistic interstellar spaceflight. Planetary and Space Science, 11(5), 485-498.
Sandberg, A., Drexler, E., & Ord, T. (2018). Dissolving the Fermi paradox. arXiv preprint arXiv:1806.02404.
Shermer, M. (2002). Why ET Hasn't Called. SciAm, 287(2), 33-33.
Tipler, F. J. (1980). Extraterrestrial intelligent beings do not exist. Quarterly Journal of the Royal Astronomical Society, 21, 267-281.
Ward, P. D., & Brownlee, D. (2003). Rare Earth: Why complex life is uncommon in the universe: Springer Science & Business Media.

I think the post is well reasoned and useful in pointing out a few shortcoming in the paper, but fails to make the point you're hoping for.
First and most importantly, with your preferred parameter choices, the 6% chance of no life in the Milky Way still almost certainly implies that the lack of alien signals is due to the fact that they are simply too far away to have been seen; the density of intelligence implied by that model is still very low. That means even your conclusion dissolves the initial "paradox." At the most, it leaves the likelihood of the existence of a future great filter, based on the evidence of not seeing alien signals, far weaker than was previously argued for.
Second, a number of your arguments seem to say that we could have counterfactual evidence, and should use that as evidence. For example, "as far as we know it is equally possible that we could have found ourselves on a 9 billion year old Earth..." (it cannot, given the habitability window for life on earth,) or "Presumably life could evolve multiple times on the same planet..." (True, but not relevant for the model, since once life has emerged it passes this step - and we see no evidence of it happening on earth..) Even if these were correct, they should be reflected in the prior or model structure, as Robin Hanson suggests ("try once steps.")
In any case, I think that a closer review of some of the data points is useful, and think the post was useful.
I haven't run the numbers, but I wouldn't be quite so dismissive. Intergalactic travel is probably possible, so with numbers as high as these, I would've expected us to encounter some early civilisation from another galaxy. So if these numbers were right, it'd be some evidence that intergalactic travel is impossible, or that something else strange is going on.
(Also, it would be an important consideration for whether we'll encounter aliens in the future, which has at least some cause prio implications.)
(But also, I don't buy the argument for these numbers, see my other comment.)
To respond to your substantive point, intergalactic travel is possible, but slow - on the order of tens of millions of years at the very fastest. And the distribution of probable civilizations is tilted towards late in galactic evolution because of the need for heavier elements, so it's unclear that early civilizations are possible, or at least as likely.
And somewhat similar to your point, see my tweet from a couple years back:
"We don't see time travelers. This means either time travel is impossible, or humanity doesn't survive.
Evidence of the theoretical plausibility of time travel is therefore strong evidence that we will be extinct in the nearer term future."
"We don't see time travelers. This means either time travel is impossible, or humanity doesn't survive.
Evidence of the theoretical plausibility of time travel is therefore strong evidence that we will be extinct in the nearer term future."
Except for the fact that those aren't the only two possibilities. There could in fact be time travelers, but they remain unseen (either purposefully or not). And this would be a possibility for a long list of reasons .
Also, don't lose the forest for the trees if you know what I mean.
Right, but the other hypotheses need large complexity penalties for why the impact of time travelling is invisible, so lack of seeing time travelers is still pretty strong evidence.
Disclaimer: this is an edited version of a much harsher review I wrote at first. I have no connection to the authors of the study or to their fields of expertise, but am someone who enjoyed the paper here critiqued and in fact think it very nice and very conservative in terms of its numbers (the current post claims the opposite). I disagree with this post and think it is wrong in an obvious and fundamental way, and therefore should not be in decade review in the interest of not posting wrong science. At the same time it is well-written and exhibits a good understanding of most of the parts of the relevant model, and a less extreme (and less wrong :) version of this post would pass my muster. In particular I think that the criticism
is very valid, and a model taking this into account would have a correspondingly higher credence for "life is common" scenarios. However the authors of the paper being criticized are explicitly thinking about the likelihood of "life is not common" scenarios (which a very naive interpretation of the Drake equation would claim are all but impossible) and here this post is deeply flawed.
The essential beef of the author of the post (henceforth the OP) with the authors of the paper (henceforth, Sandberg et al) concerns their value fl, which is the "log standard deviation in the log uncertainty of abiogenesis" (abiogenesis is the event wherein random and non-replicating chemical processes create the first replicating life). A very rough explanation of this parameter (in the log uncertainty model which Sandberg et al use and OP subscribes to) is the probability of the best currently known model for abiogenesis occuring on a given habitable planet. Note that this is very much not the probability of abiogenesis itself, since there can be many other methods which produce abiogenesis a lot more frequently than the best currently known model. The beautiful conceit of this paper (and the field it belongs to) is the idea that, absent a model for a potentially very large or very small number (in this case, the probability of abiogenesis, or, in the larger paper, the probability of the emergence of life on a given paper), our best rough estimate for our uncertainty it is more or less log uniformly distributed between the largest and smallest "theoretically possible" values (so a number between 10^-30 and 10^-40 is roughly as likely as a value between 10^-40 and 10^-50, provided these numbers are within the "theoretically possible" range. The difference between "log uniform" and "log normal" is irrelevant to a first approximation). The exact definition of "theoretically possible" is complicated, but in the case of abiogenesis the largest theoretically possible value of fl (as of any other probability measure) is 1 while the smallest possible value is the probability of abiogenesis given the best currently known methods. The model is not perfect, but by far the best we have for predicting the lower tail of such distributions, i.e., in this case, the likelihood of the cosmos being mostly devoid of intelligent life. (Note that the model doesn't tell us this probability is close to 1! Just that it isn't close to 0.)
Now the best theoretically feasible model for abiogenesis currently known is the so-called RNA world model, which is analyzed in supplement 1 of Sandberg et al. Essentially, the only sure-fire way we know of abiogenesis is spontaneously generating the genome of an archaeobacterium, which has hundreds of thousands of base pairs, and would put the probability of abiogenesis at under 10^-100,000 (insanely small). However, we are fairly confident both that much smaller self-replicating RNA sequence would be possible in certain conducive chemical environments (the putative RNA world), and that there is some redundancy in how to generate a near minimal self-replicating RNA sequence (so you don't have to get every base pair right). The issue is that we don't know how small the smallest genome is and how much redundancy there is in choosing it. By the nature of log uncertainty, if we want to get the lowest value in the range of uncertainties (what OP and Sandberg et al call log standard deviation) we should take the most pessimistic reasonable estimates. These are attempted in the previously mentioned supplement, though rather than actually taking pessimistic values, Sandberg et al rather liberally assume a very general model of self-replicating RNA formation, with their lower bound based on assumptions about protein folding (rather than a more restrictive model based on assuming low levels of redundancy, which I would have chosen, and which would have put the value of fl significantly lower even than the Sandberg et al paper: they explicitly say that they are trying to be conservative). Still, they estimate a value of fl equal or lower than 10^-30 with the current best model. In order to argue for a 10^-2 result while staying within the log normal model, OP would have to convince me of some drastic additional knowledge. Either that they have a proof, beyond all reasonable doubt, that either an RNA chain shorter than the average protein is capable of self-replicating, or that there is a lot of redundance in how self-replicating RNA can form, and a chemical "RNA soup" would naturally tend to self-replication under certain conditions. Both of these are plausible theories, but as such methods for abiogenesis are not currently known to exist, assuming they work for your lower bounds on log probability is precisely not how log uncertainty works. In this way OP is, quite simply, wrong. Therefore, as incorrect science, I do not recommend this post for the decade review.
I hadn't seen the Lineweaver and Davis paper before, thanks for pointing it out! I'm sceptical of the methodology, though. They start out with a uniform prior between 0 and 1 of the probability that life emerges in a ~0.5B year time window. This is pretty much assuming their conclusion already, as it assigns <0.1% probability to life emerging with less than 0.1% probability (I much prefer log-uniform priors). The exact timing of abiogenesis is then used to get a very modest bayesian update (less than 2:1 in favor of "life always happens as soon as possible" vs any other probability of life emerging) which yields the 95% credible interval with 13% at the bottom. Note that even before they updated on any evidence, they had already assumed a 95% credible interval with 2.5% at the bottom!
As an aside, I do mostly agree that alien life is likely to be common outside our galaxy (or at least that we should assume that it is). However, this is because I'm sympathetic to another account of anthropics, which leads to large numbers of aliens almost regardless of our prior, as I explain here.
Robin Hanson has a recent powerful argument for why if life is extremely rare, we should be extremely surprised if it originated on earth. If life needs, say, ten required steps, and the probability of each step occurring is proportional to the volume of the potential biosphere then if one planet has, say, 64 times the volume of another, all else equal, it will be 64^10 more likely to achieve all ten steps. As there are many rocky planets much bigger than earth, we should be shocked if life is rare and originated on earth.
https://www.overcomingbias.com/2020/12/try-try-or-try-once-great-filter.html
https://www.overcomingbias.com/2020/12/searching-for-eden.html
I think this is a good argument against multiple really hard steps, but doesn't say that much about the possibility of one extremely hard step.
Due to its focus on statistical reasoning and the difficulty of actioning the firmi paradox in an effective altruist context (despite how interesting and probably important it is), I've linkposted this to lesswrong.com
Thank you very much for this post, I found it very interesting. I remember reading the original paper and feeling a bit confused by it. It's not too fresh in my mind so I don't feel too able to try to defend it. I appreciate you highlighting how the method they use to estimate f_l is unique and drives their main result.
A range of 0.01 to 1 for fl in your preferred model seems surprisingly high to me, though I don't understand the Lineweaver Davis paper well enough to really comment on its result which I think your range is based on. I think they mention how their approach leaves uncertainty in n_e as to what counts as a terrestrial planet. I wonder if most estimates of any one parameter have a tendency to shift uncertainty onto other parameters, so that when combining individual estimates of each of parameter you end up with an unrealistically certain result.
"First, the approach of multiplying many parameter intervals with an upper bound at one, but no corresponding lower bound, predisposes the resulting distribution of the number of alien civilisations to exhibit a very long negative tail, which drives the reported result."
I sort of thought this was the logical structure underlying why the paradox was dissolved -- specifically that given what we know, it is totally plausible that one of the factors has a really, really low value.
There only is a paradox if we can be confindentally lower bound all of the parameters in the equation. But if given what we know there is nothing weird (ie the odds of it happening are at least 1/1000) about one of the parameters being sufficiently close to zero to make a nothing else in the visible universe likely, then we should not be surprised that we are living in such a world.
Or alternatively the description I once saw of the paper, that if god throws dice a bunch of times in creating the universe, it isn't surprising that one of the rolls came up one.
What would actually resurrect the paradox is if we could actually create lower bounds for more of the parameters, rather than simply pointing out that there isn't very good evidence that the probability is really, really low for any given one of them -- which of course there isn't.
I think typical discussions of the Fermi Paradox, such as this one, focus on the observable universe, which is finite. Assuming the universe (observable or not) is infinite, would the probability of intelligent life be 1?
If you assume the cosmological principle (i.e. that the universe in homogeneous and isotropic at the largest scales), as all modern cosmologists do, then yes. Indeed, the implication would be even more extreme, namely that the number of other civilisations in the universe is infinite as well. Whether the universe is infinite or not is an open question and depends on its curvature, which is determined by the energy density of the universe. According to our best current observations, the energy density of the universe is exactly equal to the critical density, and the universe therefore infinite and flat with zero curvature. However, a slightly higher energy density, resulting in positive curvature and a closed, i.e. finite universe, is well within our range of uncertainty. Except maybe for speculative multiverse-wide cooperation, this is of no practical relevance though, as we cannot influence anything outside of the observable universe. In fact, we can only influence events within our cosmological event horizon, which (assuming a cosmological constant) is only 16 billion light years, compared to the 46 billion light years radius of the observable universe (anything we can ever see).
Thanks for the follow-up, Jan! I agree with all your points except one. I think the best guess distribution about the energy density should be roughly continuous, which implies an infinitesimal probability of any specific value, including that implying a flat universe (which should be very close to the mode of the distribution).
That's fair. Personally, I think there is a substantive chance that an underlying theory requires the relative density to be one. This would also resolve the question of why the value is so close to one in the first place if it could've been very different (bounded by anthropic arguments I assume).
I think that estimating fl should take into account the possibility of interstellar panspermia. Life appearing once could be disseminated through the whole galaxy in a few billion years via interstellar comets.
This creates strong observation selection effect: the galaxies where panspermia is possible will create billion times more observers than non-panspermia galaxies, and we are certainly in such a galaxy. So, fl is likely to be 1.