Effective Altruism Forum
EA Forum

Hide table of contents
by Vasco Grilo🔸
3 min read 2

21

Building effective altruismForecastingAI forecastingEffective altruism fundingGrantmakingOpen Philanthropy
Frontpage

Summary

  • This analysis studies Open Philanthropy’s AI grants.
  • The grant size has become smaller (confidence of 50 %), having decreased 0.3 M$/grant/year (coefficient of determination of R^2 = 0.4 %).
  • The annual amount granted has become larger (confidence of 90 %), having increased 9 M$/year (R^2 = 40 %). Linearly extrapolating this tendency forward, the annual amount granted is predicted to be:
    • 105 M$ in 2025.
    • 170 M$ in 2030.

Acknowledgements

Thanks to Epoch[1].

Introduction

Open Philanthropy (OP) is a major funder of work which aims to reduce AI risk. Consequently, studying OP’s past AI grants may be helpful to inform efforts to decrease AI risk.

Methods

OP’s AI grants were considered as those in OP’s grants database whose focus area is Potential Risks from Advanced AI[2]. The resulting 107 grants are in tab “Grants” of this Sheets. The grant amounts were adjusted for inflation based on data from in2013dollars (see tab “Inflation”), and are expressed in 2020-$.

The following linear regressions were studied for OP’s AI grants:

  • Grant size on date.
  • Annual amount granted on year.

Results

The results were determined with this Colab. The linear regression parameters, data points, linear trends and respective 90 % confidence intervals are presented in the tables and figures below.

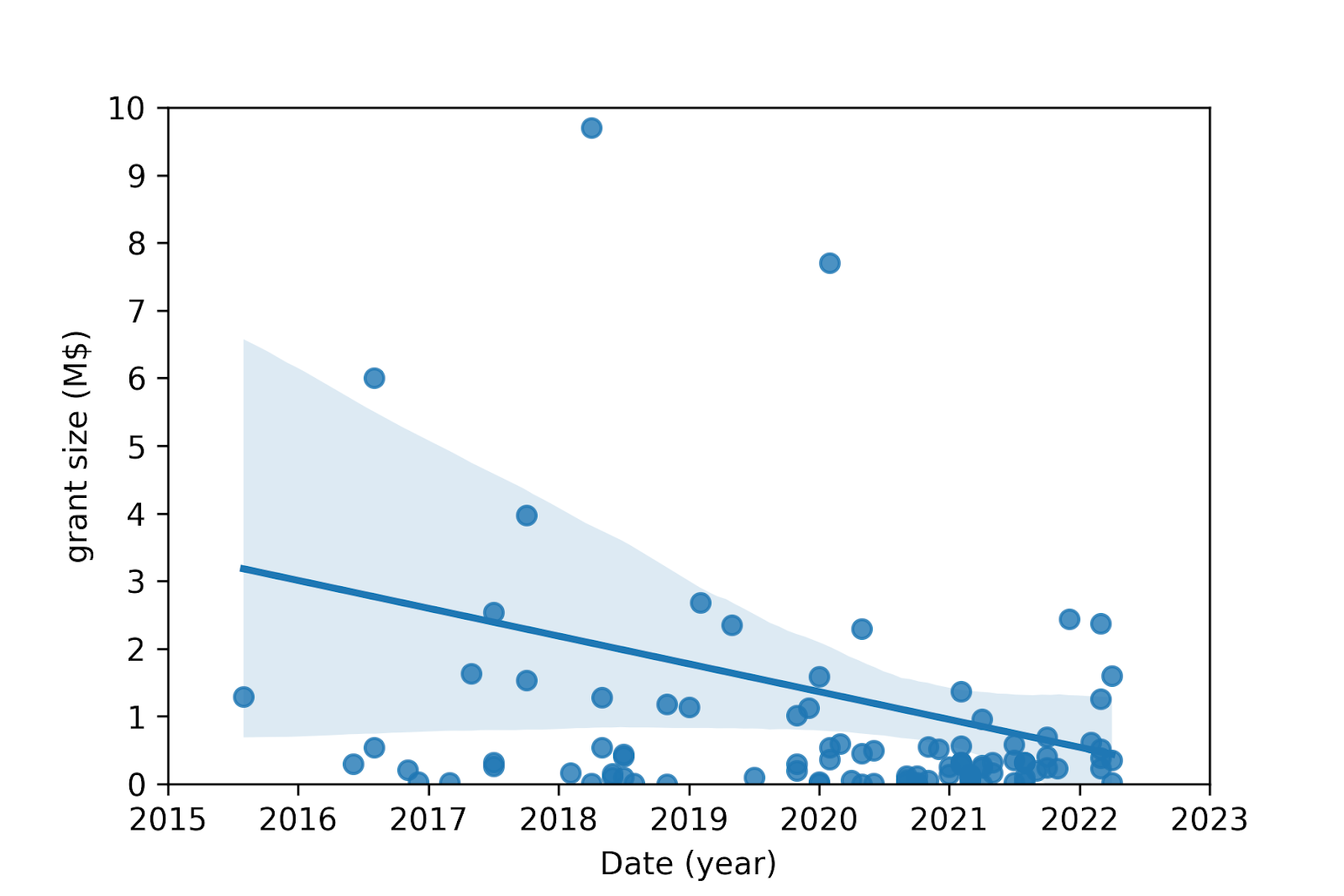
Grant size

Linear regression of grant size on date

Slope (M$/grant/year)

-0.257

Intercept (M$)

522

Correlation coefficient

-0.0601

Coefficient of determination

0.00361

P-value[3]

0.539

Standard error of the slope (M$/grant/year)

0.417

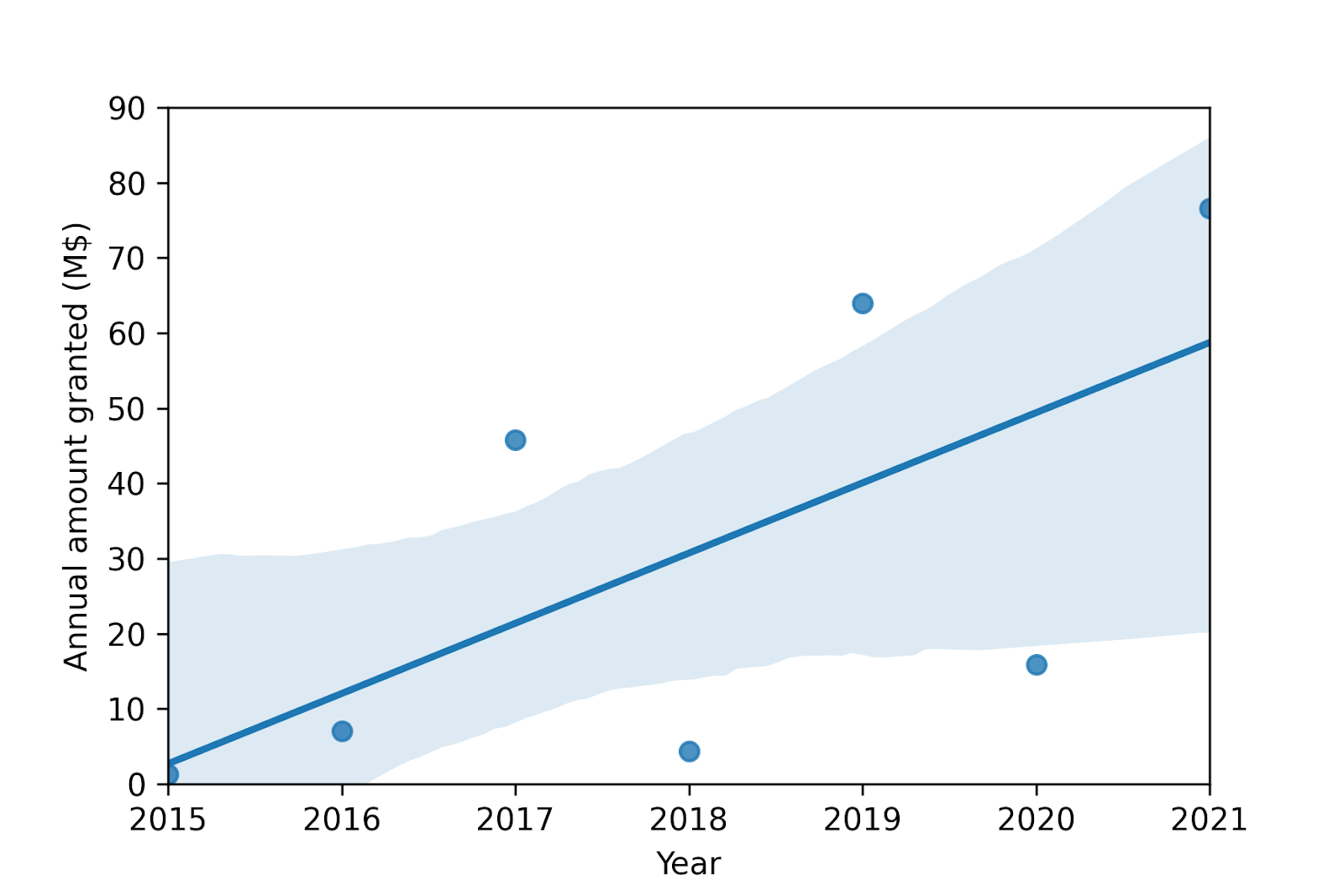
Linear regression of grant size on date. The shaded region represents the 90 % confidence interval.

Annual amount granted

Linear regression of annual amount granted on year (2015-2021)

Slope (M$/year)

9.34

Intercept (M$)

-18.8 k

Correlation coefficient

0.650

Coefficient of determination

0.423

P-value[3]

0.114

Standard error of the slope (M$/year)

4.88

Linear regression of annual amount granted on year (2015-2021). The shaded region represents the 90 % confidence interval.

Discussion

The above analysis of OP’s AI grants indicates that:

  • The grant size has become smaller (confidence of 50 % = 1 - 0.539), having decreased 0.3 M$/grant/year (R^2 = 0.4 %).
  • The annual amount granted has become larger (confidence of 90 % = 1 - 0.114), having increased 9 M$/year (R^2 = 40 %).

The trend of the grant size cannot be meaningfully extrapolated forward, given the low coefficient of determination of 0.4 %.

The trend of the annual amount granted can be projected forward more meaningfully, given the higher coefficient of determination of 40 %. Assuming an annual inflation rate of 1.75 %[4], the annual amount granted is predicted to be:

  • 105 M$ in 2025, which is 50 % larger than the 70.4 M$ of Metaculus’ community prediction (as of 25 July 2022).
  • 170 M$ in 2030, which is 40 % larger than the 125 M$ of Metaculus’ community prediction (as of 25 July 2022).
  1. ^

    This analysis was performed as part of a paid work trial at Epoch.

  2. ^

    The focus areas of the downloadable CSV file of the database are not in agreement with those of the website. The latter were considered correct, as there were only 3 grants in the CSV with focus area “Potential Risks from Advanced AI”.

  3. ^

    Considering null slope as the null hypothesis.

  1. ^

    Annual inflation rate between 2010 and 2020. Computed in cell B12 of tab “Inflation”.

Show all footnotes

21

0
0

Reactions

0
0

More posts like this

Comments2


Sorted by
New & upvoted
Click to highlight new comments since:
Thomas Kwa3
0
0

It seems like normality is violated on the first graph, have you tried taking a log transform or something?

Reply
Vasco Grilo🔸1
0
0

Thanks for commenting!

I had not tested it, but your are kind of right! Applying the Shapiro-Wilk normality test to:

  • The grant size results in a p-value of 3*10^-20 (for the null hypothesis "the grant size follows a normal distribution"). 
  • The logarithm of the grant size results in a p-value of 0.3 (for the null hypothesis "the grant size follows a lognormal distribution").

So it looks like we can confidently reject the grant size following a normal distribution, but it could well follow a lognormal distribution. This aligns well with my expectations.

Reply
More from Vasco Grilo🔸
92
Yes, Shrimp Matter
Vasco Grilo🔸
· · 8m read
10
10
34
Cost-effectiveness of Veganuary and School Plates
Vasco Grilo🔸
· · 11m read
8
8
98
GiveWell may have made 1 billion dollars of harmful grants, and Ambitious Impact incubated 8 harmful organisations via increasing factory-farming?
Vasco Grilo🔸
· · 11m read
108
108
View more
Curated and popular this week
LintzA
 ·  · 15m read
 · 
Cross-posted to Lesswrong Introduction Several developments over the past few months should cause you to re-evaluate what you are doing. These include: 1. Updates toward short timelines 2. The Trump presidency 3. The o1 (inference-time compute scaling) paradigm 4. Deepseek 5. Stargate/AI datacenter spending 6. Increased internal deployment 7. Absence of AI x-risk/safety considerations in mainstream AI discourse Taken together, these are enough to render many existing AI governance strategies obsolete (and probably some technical safety strategies too). There's a good chance we're entering crunch time and that should absolutely affect your theory of change and what you plan to work on. In this piece I try to give a quick summary of these developments and think through the broader implications these have for AI safety. At the end of the piece I give some quick initial thoughts on how these developments affect what safety-concerned folks should be prioritizing. These are early days and I expect many of my takes will shift, look forward to discussing in the comments!  Implications of recent developments Updates toward short timelines There’s general agreement that timelines are likely to be far shorter than most expected. Both Sam Altman and Dario Amodei have recently said they expect AGI within the next 3 years. Anecdotally, nearly everyone I know or have heard of who was expecting longer timelines has updated significantly toward short timelines (<5 years). E.g. Ajeya’s median estimate is that 99% of fully-remote jobs will be automatable in roughly 6-8 years, 5+ years earlier than her 2023 estimate. On a quick look, prediction markets seem to have shifted to short timelines (e.g. Metaculus[1] & Manifold appear to have roughly 2030 median timelines to AGI, though haven’t moved dramatically in recent months). We’ve consistently seen performance on benchmarks far exceed what most predicted. Most recently, Epoch was surprised to see OpenAI’s o3 model achi
Dr Kassim
 ·  · 4m read
 · 
Hey everyone, I’ve been going through the EA Introductory Program, and I have to admit some of these ideas make sense, but others leave me with more questions than answers. I’m trying to wrap my head around certain core EA principles, and the more I think about them, the more I wonder: Am I misunderstanding, or are there blind spots in EA’s approach? I’d really love to hear what others think. Maybe you can help me clarify some of my doubts. Or maybe you share the same reservations? Let’s talk. Cause Prioritization. Does It Ignore Political and Social Reality? EA focuses on doing the most good per dollar, which makes sense in theory. But does it hold up when you apply it to real world contexts especially in countries like Uganda? Take malaria prevention. It’s a top EA cause because it’s highly cost effective $5,000 can save a life through bed nets (GiveWell, 2023). But what happens when government corruption or instability disrupts these programs? The Global Fund scandal in Uganda saw $1.6 million in malaria aid mismanaged (Global Fund Audit Report, 2016). If money isn’t reaching the people it’s meant to help, is it really the best use of resources? And what about leadership changes? Policies shift unpredictably here. A national animal welfare initiative I supported lost momentum when political priorities changed. How does EA factor in these uncertainties when prioritizing causes? It feels like EA assumes a stable world where money always achieves the intended impact. But what if that’s not the world we live in? Long termism. A Luxury When the Present Is in Crisis? I get why long termists argue that future people matter. But should we really prioritize them over people suffering today? Long termism tells us that existential risks like AI could wipe out trillions of future lives. But in Uganda, we’re losing lives now—1,500+ die from rabies annually (WHO, 2021), and 41% of children suffer from stunting due to malnutrition (UNICEF, 2022). These are preventable d
Rory Fenton
 ·  · 6m read
 · 
Cross-posted from my blog. Contrary to my carefully crafted brand as a weak nerd, I go to a local CrossFit gym a few times a week. Every year, the gym raises funds for a scholarship for teens from lower-income families to attend their summer camp program. I don’t know how many Crossfit-interested low-income teens there are in my small town, but I’ll guess there are perhaps 2 of them who would benefit from the scholarship. After all, CrossFit is pretty niche, and the town is small. Helping youngsters get swole in the Pacific Northwest is not exactly as cost-effective as preventing malaria in Malawi. But I notice I feel drawn to supporting the scholarship anyway. Every time it pops in my head I think, “My money could fully solve this problem”. The camp only costs a few hundred dollars per kid and if there are just 2 kids who need support, I could give $500 and there would no longer be teenagers in my town who want to go to a CrossFit summer camp but can’t. Thanks to me, the hero, this problem would be entirely solved. 100%. That is not how most nonprofit work feels to me. You are only ever making small dents in important problems I want to work on big problems. Global poverty. Malaria. Everyone not suddenly dying. But if I’m honest, what I really want is to solve those problems. Me, personally, solve them. This is a continued source of frustration and sadness because I absolutely cannot solve those problems. Consider what else my $500 CrossFit scholarship might do: * I want to save lives, and USAID suddenly stops giving $7 billion a year to PEPFAR. So I give $500 to the Rapid Response Fund. My donation solves 0.000001% of the problem and I feel like I have failed. * I want to solve climate change, and getting to net zero will require stopping or removing emissions of 1,500 billion tons of carbon dioxide. I give $500 to a policy nonprofit that reduces emissions, in expectation, by 50 tons. My donation solves 0.000000003% of the problem and I feel like I have f
Recent opportunities in Building effective altruism
3
Apply to become a Futurekind AI Facilitator or Mentor (deadline: April 10)
Jay Luong
· · 2m read
0
0
35
AIS Netherlands is looking for a Founding Executive Director (EOI form)
7 authors
· · 5m read
4
4
33
Announcing the Vancouver Forum for Effective Altruism, April 4-5
Danielle MacLean
· · 1m read
4
4
View more