TLDR
We introduce an inequality for deciding when scientific research should be funded and two simple Guesstimate models for estimating the cost-effectiveness of scientific research. Depending on the exact assumptions, our simulations suggest that strategically funding scientific research designed to enable or develop better interventions can be at least 2-5 times as cost-effective as investing everything into the interventions that happen to already exist today.
1. Introduction
Scientific research can significantly improve our capacity to prevent or ameliorate human suffering and foster well-being (Lieder & Prentice, 2022; Lieder, Prentice, & Corwin-Renner, 2022). However, so far, the possibility that funding scientific research that might enable more effective interventions might be highly cost-effective has received little attention. In a first exploration of this distinction, Jack Malde concluded that we should initially prioritize investing in scientific research over investing in interventions that already exist. By contrast, casual observation suggests that some grant makers, such as GiveWell, spend less than 1% of their budget on scientific research.
To help Effective Altruists think through the question of how we should allocate our funds between scientific research that might lead to better interventions and the best intervention that are already available, we created a Guesstimate model anyone can use to compare the cost-effectiveness of applying what we already know versus conducting research to improve it. The remainder of this post explains this model and reports the results of a series of simulations that estimate the cost-effectiveness of scientific research. Before we dive into those details in Sections 3-5, the next section explains the basic idea with a simple equation that provides a lower bound on the value of research.
2. A simple lower bound on the value of research
Let’s say that the total amount of funding is m dollars and the probability of investing c dollars into the research generates an intervention that is at least n times as effective as the best existing intervention with probability p. If the cost-effectiveness of the best intervention that already exists is CE_prev, then successful research would generate an intervention with a cost-effectiveness of at least n*CE_prev. Investing the remaining funds (i.e., m-c dollars) into that new intervention would generate n*CE_prev*(m-c) units of good. Therefore, the expected amount of good that such research would achieve is at least p*n*CE_prev*(m-c). This is a lower bound because it does not take into account that the cost-effectiveness ratio could also be (substantially) larger than n. The amount of good we would be missing out on by not investing all the funds directly into the best existing intervention would be c*CE_prev. Therefore, funding the research would allow us to do more good as soon as p*(n-1) is greater than c/(m-c). This is an upper bound on how high p and n because it substitutes the expected benefit of research by the simple lower bound derived above. This means that some research projects may be worth funding even when they don’t fulfill this inequality. However, when a research project does fulfill this inequality, then it is definitely worth funding. For instance, when the total budget is 1 billion dollars, then this equation entails that a research project that costs 1 million dollars (c/(m-c)=0.001) is worth funding if it has at least a 1% chance (p=0.01) of producing an intervention that is at least 10% more cost-effective (n=1.1) than the best existing intervention. This is a surprisingly low bar relative to how hard it is to get funding for EA-aligned academic research. This simple analysis therefore suggests that funding EA-aligned academic research is a highly neglected and highly cost-effective opportunity for grant makers to improve the future of humanity.
We can also use this simple inequality to determine how low the chances of finding or developing a better intervention would have to be so that it were optimal to invest only 0.5% of the total budget into research, as GiveWell apparently does (see Footnote 1). Granted that additional research often has diminishing returns, our inequality suggests that investing no more than 3 out of 515 million dollars into research (c/(m-c)=0.006) is optimal only if the probability of finding an intervention that is at least 10% more cost-effective than the best existing intervention is at most 6% (p=(c/(m-c))/(n-1)=0.006/0.1=0.06). This seems implausibly pessimistic. If our chances of improving the cost-effectiveness of interventions for saving lives or alleviating poverty by at least 10% were at least 50%, then this would be worth investing up to 4.8% of the budget, which almost 10 times as much as GiveWell’s current investment into research.
All of these numbers are only lower bounds. The real value of research might be substantially greater. In fact, as documented below, our most realistic simulations suggest that it would be optimal to allocate at least the first 8% of the budget to scientific research. As a bridge from the simple inequality to those more complex simulations, the following section presents a probabilistic model that allows us to dispense with the simplistic assumption that research either produces a new intervention that is exactly n times as cost-effective as the best existing intervention or fails to achieve any improvement whatsoever. It should therefore be able to provide a more accurate estimate of the expected value of research.
3. A first model of the cost-effectiveness of scientific research
Inspired by McGuire and Plant (2021), we created a simple Guesstimate model of the cost-effectiveness of scientific research (see Figure 1). The model illustrated in Figure 1 is freely available for anyone to use. You can access it at https://www.getguesstimate.com/models/20588. The following paragraphs explain each of the model’s components and assumptions in turn.
The final output of the model is a probability distribution over the ratio of the cost-effectiveness of scientific research and the cost-effectiveness of investing all the funds into the best existing intervention (CE_ratio). A ratio greater than 1 means that investing a certain amount of money into research is more cost-effective than investing everything into deploying the best existing interventions. The model defines the cost-effectiveness of research (CE_research) as the quotient of the value of research (VOR) and the research costs (RC), that is, CE_research = VOR/RC. We model the cost of the research as a Log-Normal distribution with 95% of its probability mass between $250,000 and $2,500,000.
Figure 1. Guesstimate model of the relative cost-effectiveness of research.
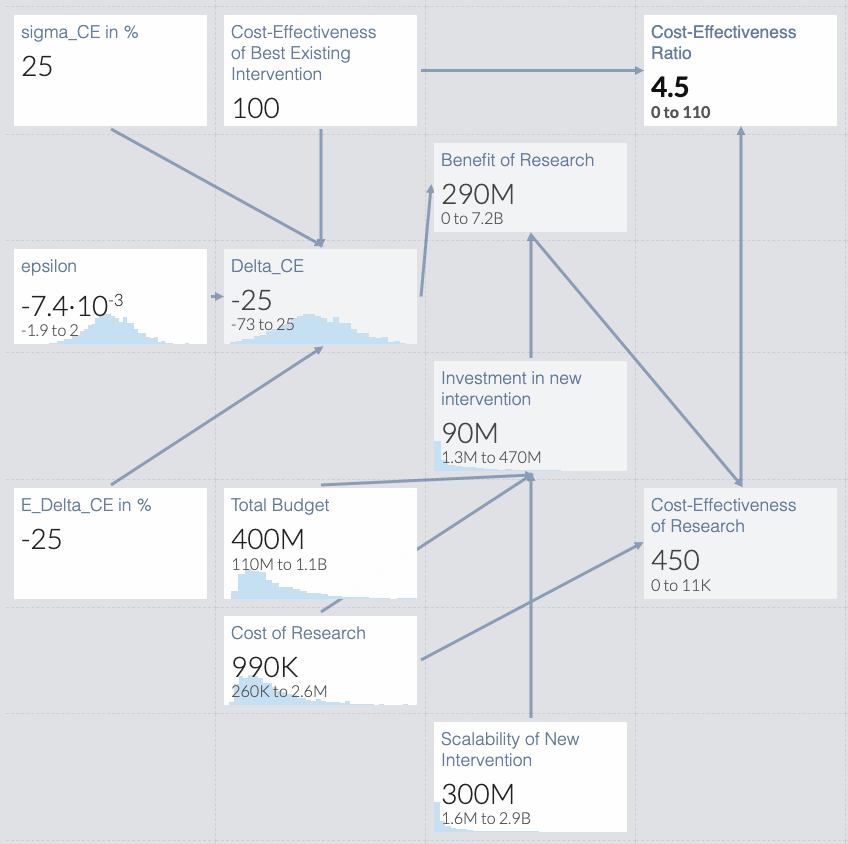
Building on the value of information framework (Howard, 1966), we model the VOR as the expected value of the opportunities we would have to invest money in good causes after the research has been completed minus the value of the opportunities that are already available. To obtain a lower bound on the value of research, we assume that its only benefit will be to add a new intervention to the repertoire of interventions that EAs and EA organizations can fund. We model the value of either decision situation as the amount of good that can be created by investing a fixed budget into the best available intervention. The amount of good we can create without the research is the product of the budget and the cost-effectiveness of the best intervention that already exists (i.e., budget*CE_prev). The amount of good that can be created after a research project has produced a new intervention with cost-effectiveness CE_new is the product of the amount of money that can be invested in interventions (budget) and the maximum of the cost-effectiveness of the new intervention and the best previous intervention (i.e., max{CE_prev, CE_new}). Under these assumptions, the value of research is
VOR = E[budget * max(CE_prev, CE_new)] - E[budget*CE_prev]
= E[budget * max(CE_new-CE_prev, 0)].
This assumes that the intervention resulting from the research will be deployed if and only if it is more cost-effective than the best existing intervention.
The amount of money that could be invested in the new intervention (budget) would be constrained by the scalability of the new intervention and the remaining budget available for increasing human well-being, that is
budget = min(scalability, total funds - research costs),
where scalability is the amount of money that could be invested into the deployment of the new intervention before it becomes substantially less cost-effective. The scalability of new interventions can vary widely. Some may be specifically designed for a small, highly specialized group, such as AI researchers, whereas others might be designed for the general public. We therefore assume that the scalability of a new intervention follows a log-Normal distribution that has 95% of its probability mass on the interval between 1 million dollars and 1 billion dollars. Moreover, we assume that the total funds are between 100 million dollars and 10 billion dollars, which is approximately the endowment of Open Philanthropy. We therefore model the total budget as a draw from a log-Normal distribution with the 95% confidence interval [$100M, $1B].
The next crucial component of the value of research is the cost-effectiveness of the new intervention relative to the cost-effectiveness of the best existing intervention. In the following analysis, we investigate how the value of research depends on one’s assumptions about how likely additional research is to produce new interventions with different levels of effectiveness.
It has been pointed out that the cost-effectiveness of charities follows a heavy-tailed distribution, with most charities being relatively ineffective and some charities being more than 100 times as effective as the average charity (MacAskill, 2015). It is not clear to which extent this would also apply to new interventions produced by research that is specifically designed to produce highly cost-effective interventions. Therefore, to obtain a lower bound on the value of research, we first model the cost-effectiveness of new interventions resulting from such research as a Normal distribution and then explore how much higher the predicted cost-effectiveness of research is if you assume a heavy-tailed. In both cases, we systematically investigate the effect of different assumptions about the expected value of the cost-effectiveness of new interventions and the variability in the cost-effectiveness of new interventions.
Concretely, we model the relative difference between the cost-effectiveness of the new intervention and the cost-effectiveness of the new intervention (Diff_CE) as a Normal distribution with mean M_Diff_CE and standard deviation SD_Diff_CE. Concretely, we model the difference between cost-effectiveness of the new intervention and the cost-effectiveness of the previous intervention as
Diff_CE = CE_prev*(M_Diff_CE + SD_CE*epsilon)/100%,
where epsilon ~ N(0, 1) is the unknown amount by which a new intervention will be more or less cost-effective than expected. The parameter M_Diff_CE specifies the systematic difference between the average cost-effectiveness of new interventions and the cost-effectiveness of the best already existing intervention as a percentage of the cost-effectiveness of the best-existing intervention. The parameter SD_CE specifies the size of the non-system, random variation in the cost-effectiveness of new interventions as a percentage of the cost-effectiveness of the best already existing intervention. Its value determines how likely it is that a new intervention will be much better (or much worse) than the best intervention that already exists. You can think of it as a measure of how uncertain a well-informed person should be about the potential practical utility of the potential future findings of research in a given area.
For the sake of illustration, let’s assume that, on average, the new interventions that come out of research projects are 10% worse than the best interventions that are already available. In this case, M_Diff_CE is -10%. Moreover, let’s assume that 95% of the time the cost-effectiveness of a new intervention lies within ±20% of its average. In that case, the standard deviation of the cost-effectiveness of new interventions is about 10% (SD_CE=10%). Then, a research project has a 16% chance of generating a new intervention that is more cost-effective than the best existing intervention, and a 2.3% chance to produce a new intervention that is at least 10% more cost-effective than the best existing intervention. Now, if the cost-effectiveness of new interventions were twice as uncertain (i.e., SD_CE=20%), then there would be 31% chance that a single research project would produce a superior intervention and a 16% chance that the new intervention would be at least 10% more cost-effective than the best existing intervention.
In general, we can estimate the upside potential of developing a new intervention by calculating the probability that the new intervention will be x% more effective than the best previous intervention. Assuming that the effectiveness of the new intervention is normally distributed, this probability is 1-F((x-M_Diff_CE)/SD_CE), where F is the cumulative distribution function of the standard Normal distribution. Thus, for any fixed assumption about the average cost-effectiveness of the new interventions that research in a given area might produce, the probability of achieving a large improvement increases with SD_CE. Therefore, everything else being equal, research is more valuable when SD_CE is high.
Critically, developing new interventions only adds to the set of options we can choose between. This means that we will only deploy the new intervention if it is more cost-effective than the best interventions we already have. Therefore, the actual change in cost-effectiveness resulting from the research is not Diff_CE but max(0,Diff_CE). In our example, this increases the expected change in cost-effectiveness from M_Diff_CE=-10% to E[max(0,Diff_CE)]≈+1% when SD_CE=10% and E[max(0,Diff_CE)]≈+4% when SD_CE=20%. Thus, even though the expected cost-effectiveness of the intervention resulting from the second project is -10%, such a project is nevertheless four times as valuable as a research project that is 100% certain to produce an intervention that is 1% more cost-effective than the best existing intervention.
4. Results: Scientific research could be more cost-effective than applying what we already know
We explored the value of research across several scenarios that differ in the mean (M_Diff_CE) and the standard deviation (SD_Diff_CE) of the difference between the cost-effectiveness of the new intervention resulting from the research and the best intervention that already exists. Given that the best existing intervention is usually the result of the best previous research, our analysis focuses on scenarios where new interventions are, on average, at most as cost-effective as the best already existing intervention (M_Diff_CE<0) but have some chance of being more cost-effective. Tables 1 and 2 summarize the scenarios we investigated and the results we obtained for each scenario, assuming that the cost-effectiveness of new interventions follows a Normal distribution (Table 1) and a Log-Normal distribution (Table 2), respectively. We first present the lower bounds we obtained by assuming that the cost-effectiveness of new interventions is drawn from a Normal distribution. For each scenario, we report how likely the research is to produce an intervention that is more cost-effective than the best intervention that is already available (i.e., P(CE_new>CE_prev)) and the research’s cost-effectiveness (CE_research) relative to investing everything into the best intervention that already exists (CE_research/CE_prev).
The first set of scenarios corresponds to efforts to improve the cost-effectiveness of the best existing intervention. We assume that in these scenarios the expected change in the cost-effectiveness of the intervention is zero and that its standard deviation is relatively small (1% <= SD_CE <= 20%). As summarized in Table 1, we found that, in this scenario, investing in research pays off if the standard deviation of the cost-effectiveness of new interventions is at least 2% of the cost-effectiveness of the existing intervention. In terms of the upside potential that is required to make research on improving the best existing intervention worthwhile, this means that additional research is warranted as long as there is still at least a 5% chance to increase the cost-effectiveness of the intervention by at least 4%. This is a very low bar. We think it is very likely that this criterion is met for research on improving upon most, if not all, of the most cost-effective interventions that have been developed so far. Moreover, even when there is only a 5% chance to achieve an improvement of at least 10% (which is the case if SD_CE ≥ 5%), the benefit of funding the research is 3.3 times as cost-effective as investing everything in the current version of the intervention without improving it first. Moreover, as the uncertainty about the cost-effectiveness of the new intervention increases to SD_CE=10% and SD_CE=20%, research becomes 6.6x and 13x as cost-effective as the best intervention that already exists, respectively.
Our second and our third scenario concern investing in research in other areas that have yet to produce competitive interventions. In those cases, the new interventions might be less cost-effective than the best existing intervention on average. However, assuming that there has been comparatively less research in those areas, it is possible that some new interventions could be substantially more cost-effective than the already established intervention. We therefore consider two hypothetical research topics where the interventions that have been created based on what is already known are only 75% (Scenario 2) and 50% as cost-effective as the best established intervention (Scenario 3), respectively. The results for SD_CE=20% show that research on the former topic (Scenario 2) is more than twice as cost-effective as the established intervention, as long as it has at least a 10.6% chance of discovering a more effective intervention (see Table 1). Moreover, the results for SD_CE=25% reveal that if such research has an at least 15% chance of producing a superior intervention, then it is at least 4.5 times as cost-effective as the best existing intervention.
Similarly, we found that funding research in an area where the best interventions are only half as cost-effective as the best existing intervention (Scenario 3) breaks even with investing all funds in the deployment of the established intervention around the point where the research has a 3% chance of producing a superior intervention. This is the case when SD_CE is between 25% and 30% (see Table 1). Moreover, the results for SD_CE ≧ 30% suggest that when the chance of obtaining a more cost-effective intervention is 5% or 8%, then funding such research is more than 1.8 times and 3.2 times as cost-effective as investing directly in the deployment of the best existing intervention, respectively. Overall, these findings suggest that funding scientific research outside the cause area with the most cost-effective existing interventions can also be highly cost-effective.
In summary, across all considered scenarios, the average cost-effectiveness of research was about 3.2 times as high as the cost-effectiveness of investing everything in the best intervention that already exists, and its median cost-effectiveness was 2.1 times as high as the cost-effectiveness of investing everything into the best existing intervention.
Table 1: Summary of results from Scenarios 1, 2 and 3 depending on the standard deviation of the cost-effectiveness of the new intervention resulting from the research (i.e., SD_CE).
Scenario | Results | ||||
Nr | Distribution of CE_new | M_Diff_CE | SD_CE | Probability that research will produce a superior intervention | Compared to investing everything into the best intervention that already exists, first investing in research is __ times as cost-effective |
1 | Normal | 0% | 1% | 50.0% | 0.7 |
1 | Normal | 0% | 2% | 50.0% | 1.3 |
1 | Normal | 0% | 5% | 50.0% | 3.3 |
1 | Normal | 0% | 10% | 50.0% | 6.6 |
1 | Normal | 0% | 20% | 50.0% | 13.0 |
2 | Normal | -25% | 10% | 0.6% | 0.1 |
2 | Normal | -25% | 15% | 4.8% | 0.9 |
2 | Normal | -25% | 20% | 10.6% | 2.4 |
2 | Normal | -25% | 25% | 15.9% | 4.5 |
2 | Normal | -25% | 30% | 30.9% | 6.8 |
3 | Normal | -50% | 20% | 0.6% | 0.2 |
3 | Normal | -50% | 25% | 2.3% | 0.8 |
3 | Normal | -50% | 30% | 4.8% | 1.8 |
3 | Normal | -50% | 35% | 7.7% | 3.2 |
Note. In Scenario 1 the cost-effectiveness of the new intervention is equal to the cost-effectiveness of the best already existing intervention (M_Diff_CE=0%). In Scenario 2 it is 25% lower, and in Scenario 3 it is 50% lower. SD_CE expresses the standard deviation of the random variation in the cost-effectiveness of new interventions as a percentage of the cost-effectiveness of the best intervention that already exists (CE_prev).
Our model makes a number of assumptions. To determine which of these assumptions are critical for our conclusions, we performed a sensitivity analysis. We found that the results of our analysis are reasonably robust to our auxiliary assumptions. Concretely, we found that variation of the total funds within the assumed range of 100 million to 1 billion dollars accounted for only about 5% of the variance in the cost-effectiveness ratio (R2=0.05). Moreover, the cost of research (R2=0.01) and the scalability of new interventions (R2=0.01) each accounted for only 1% of the variance in the cost-effectiveness ratio.
Table 2. Cost-Effectiveness of research if the effect-sizes of new interventions follow a heavy-tailed log-Normal distribution with the same mean and variance as in the corresponding scenario in Table 1.
Scenario | Results | ||||
| Nr |
Distribution of CE_new | M_Diff_CE | SD_CE | Probability that research will produce a superior intervention | Compared to investing everything into the best intervention that already exists, first investing in research is __ times as cost-effective |
1 | Log-Normal | 0% | 1% | 49.8% | 0.7 |
1 | Log-Normal | 0% | 2% | 49.6% | 1.3 |
1 | Log-Normal | 0% | 5% | 49.0% | 3.3 |
1 | Log-Normal | 0% | 10% | 48.0% | 6.7 |
1 | Log-Normal | 0% | 20% | 45.1% | 15.0 |
2 | Log-Normal | -25% | 10% | 1.3% | 0.2 |
2 | Log-Normal | -25% | 15% | 6.0% | 1.9 |
2 | Log-Normal | -25% | 20% | 11.0% | 4.4 |
2 | Log-Normal | -25% | 25% | 14.7% | 7.6 |
2 | Log-Normal | -25% | 30% | 17.4% | 11.0 |
3 | Log-Normal | -50% | 20% | 2.3% | 1.7 |
3 | Log-Normal | -50% | 25% | 4.4% | 3.4 |
3 | Log-Normal | -50% | 30% | 6.3% | 6.4 |
3 | Log-Normal | -50% | 35% | 7.9% | 9.3 |
Another potentially critical assumption of our model is that the effect-sizes of new interventions follow a Normal distribution. It has previously been argued that the effectiveness of charities follows a heavy-tailed distribution, with most charities being rather ineffective and some charities being orders of magnitude more effective (MacAskill, 2015). It is therefore conceivable, that the effect size of new interventions might follow a heavy-tailed distribution rather than a Normal distribution. To explore the implications of this possibility, we repeated the simulations reported in Table 1 with a Guesstimate model where the effect sizes of the new intervention being drawn from a heavy-tailed Log-Normal distribution instead of a Normal distribution (see https://www.getguesstimate.com/models/20653). Keeping the expected value and the variance of the cost-effectiveness of new interventions constant, we found that the cost-effectiveness of research remains similar when SD_CE is at most 10% but starts to grow increasingly larger when beyond that point (see Table 2). Concretely, if you assume a Log-Normal distribution, then research is worthwhile in all considered scenarios where the variability of the cost-effectiveness of new interventions is at least 15%. Moreover, it increased the predicted cost-effectiveness of research in scenarios 2 and 3 from at most 6.8x to up to 11x the cost-effectiveness of deploying the best intervention that already exists (average: 5.1x, median: 4.4x; see Table 2). This is because assuming a Log-Normal distribution increases both the likelihood of finding a superior intervention in those scenarios and the extent to which any superior interventions that might be found are more cost-effective than the best existing intervention. Overall, across all three scenarios, the average cost-effectiveness ratio was 5.2, which is 1.6 times as high as the average cost-effectiveness ratio we obtained assuming a Normal distribution.
5. Discussion
We have created a public Guesstimate models that the EA community can use to explore the cost-effectiveness of funding applied research and use-inspired basic research. The model assuming a Normal distribution is available at https://www.getguesstimate.com/models/20588 and the model assuming a heavy-tailed distribution is available at https://www.getguesstimate.com/models/20653.
The cost-effectiveness of research is likely even higher than our analysis suggested. Our cost-effectiveness analysis provides merely a lower bound on the value of research because it assumes that the scientists will only have a single attempt to produce a more cost-effective intervention. In reality, however, additional research projects can be funded if the first one does not succeed. Moreover, even when the first project succeeds to produce a more cost-effective intervention, the community could invest further funds in research aiming to produce even more cost-effective interventions. Future work should explore the implications of the sequential nature of this investment problem on the cost-effectiveness of research. Another reason why scientific research is likely even more cost-effective than our analysis suggests is that it can also positively influence the future of humanity in a more indirect way. Academic research often lays the foundations for later discoveries and applications that can be very difficult to predict. Moreover, academic research can positively influence the attitudes and decisions of intellectuals, leaders, and the general public even without it being translated into an intervention.
The scenarios reported in Tables 1 and 2 differ in the expected value and the standard deviation of the difference in cost-effectiveness attained by a new intervention. Those differences correspond to differences between research areas. In established areas where substantial amounts of research have already been conducted, it is generally harder to find interventions that are substantially more cost-effective than the best existing intervention in that area. This corresponds to a larger negative value of M_Diff_CE and a lower value of SD_CE. By contrast, in more neglected research areas, there is more room for improvement. We modeled this by considering higher values for SD_CE.
Our cost-effectiveness analysis used the same decision-theoretic value-of-information framework as MacAskill, Bykvist, and Ord (2020). The main conceptual difference is that we applied this framework to determine the value of expanding the set of possible actions, rather than the value of moral information.
We found that the cost-effectiveness of research partly depends on whether the cost-effectiveness of new interventions follows a Normal distribution or a heavy-tailed distribution (cf. Table 2 vs. Table 1). Whether the distribution of effect sizes is heavy-tailed is an empirical question that can be answered by inspecting the histograms of the effect sizes reported in meta-analyses. However, regardless of the assumed shape of the distribution, our results suggest that funding research first is more cost-effective than investing everything into interventions that already exist.
All in all, our results suggest that funding scientific research that aims to either increase the cost-effectiveness of the best existing interventions or discover novel interventions that are highly cost-effective might often be substantially more cost-effective than investing immediately in the deployment of the best existing interventions. This opportunity to do good appears to be highly neglected by the EA community. This raises two questions to be addressed in future research:
- What are the most impactful research topics that should receive more funding?
- Which proportion of their funds should philanthropic organizations, such as Open Philanthropy and the Gates Foundation, invest in scientific research?
The first question can be answered by applying the very general approach we introduced here to estimate and compare the cost-effectiveness of research on specific topics. We hope that this will lead to a prioritized list of the most important scientific questions (from an EA perspective), along with estimates of how the cost-effectiveness of research on each topic compares to the cost-effectiveness of the best existing interventions for promoting human well-being. As a proof-of-concept, I have recently estimated the cost-effectiveness of research on a specific behavioral science topic: promoting prosocial behavior. Scaling up this approach has to be a team effort. If you are potentially interested in contributing, you can read more about this project here. To address the second question, we conducted additional probabilistic simulations, that we will report in a later post.
Author Contributions
Falk Lieder derived the inequality, developed the Guesstimate models, ran the simulations, wrote the first draft, and revised it.
Joel McGuire contributed to the development of the ideas presented in this post, conceived the argument in the second paragraph of Section 2, wrote Footnote 1, gave feedback on earlier versions of the model, suggested the exploration of power law distributions and other future directions, and gave insightful feedback on earlier versions of this post.
Emily Corwin-Renner encouraged ideas to this project, gave insightful feedback on earlier versions of this post, and helped revise it.
Acknowledgements
This analysis is part of the research priorities project, which is an ongoing collaboration with Izzy Gainsburg, Philipp Schönegger, Emily Corwin-Renner, Abbigail Novick Hoskin, Louis Tay, Isabel Thielmann, Mike Prentice, John Wilcox, Will Fleeson, and many others. The model is partly inspired by Jack Malde’s earlier post on whether effective altruists should fund scientific research. We would like to thank Michael Plant from the Happier Lives Institute, Emily Corwin-Renner, Cecilia Tilli, and Andreas Stuhlmüller for helpful pointers, feedback, and discussions.
References
- Howard, R. A. (1966). Information value theory. IEEE Transactions on systems science and cybernetics, 2(1), 22-26.
- Lieder, F., & Prentice, M. (in press). Life Improvement Science. In F. Maggino (Ed.), Encyclopedia of Quality of Life and Well-Being Research, 2nd Edition, Springer. https://doi.org/10.13140/RG.2.2.10679.44960
- Lieder, F., Prentice, M., & Corwin-Renner, E. R. (2022). An interdisciplinary synthesis of research on understanding and promoting well-doing. OSF Preprint
- MacAskill, W. (2015). Doing Good Better: Effective Altruism and How You Can Make a Difference. Random House.
- MacAskill, M., Bykvist, K., & Ord, T. (2020). Moral uncertainty. Oxford University Press.
- McGuire, J., & Plant, M. (2021, October). Strong Minds: Cost-Effectiveness Analysis. Technical Report. Happier Lives Institute. https://www.happierlivesinstitute.org/report/psychotherapy-cost-effectiveness-analysis/

Thanks for this work, Falk! I am excited to test this model when I have time and to see further related developments.
At the moment, I lack a clear sense of how this model is useful in practice. I'd like to see the model applied to justify a new project, or evaluate the returns on a previous one.
BTW, I discussed if we could use value of information for research funding/evaluation with Sam Nolan just last week. I encouraged him to speak with you about this work. It might be worth reaching out if he hasn't already.
Thank you, Peter! I am working on a proof-of-concept showing that this approach can be used to identify promising research topics and to choose between specific projects. I am planning to post about it next week. I will keep you posted.
Here is my post on the proof-of-concept that this approach can be applied to predict the cost-effectiveness of funding more research on a specific topic: https://forum.effectivealtruism.org/posts/aRFCrJaozrHearPAh/doing-research-on-promoting-prosocial-behavior-might-be-100
Hey! Love the post. Just putting my comments here as they go.
Tldr This seems to be a special case of the more general theory of Value of Information. There's a lot to be said about value of information, and there are a couple of parameter choices I would question.
The EA Forum supports both Math and Footnotes now! Would be lovely to see them included for readability.
I'm sure you're familiar with Value of Information. It has a tag on the EA Forum. It seems as if you have presumed the calculations around value of information (For instance, you have given a probability p and better-than-top-charity ratio n, both of which can be explicitly calculated with Value of Information). The rest of the calculations seem valid and interesting.
I might be wrong, but I think this is assuming that this is the only research project that is happening. I could easily assume that EA spends more than 0.1% of it's resources on identifying/evaluting new interventions. Although, I'm yet to know of how to do the math with multiple research projects. It's currently a bit beyond me.
There's a common bias to choose numbers within, say 104 and 10−3 that may bias this investigation. For instance, when I calculated the value of information on GiveDirectly, when n>1 was p<10−12. If you are unsure about whether a charity is cost-effective, often the tails of your certainty can drop fast.
Your "lower bound" is entirely of your own construction. It's derived from your decleration at the start that p is the chance that you find a "investing c dollars into the research generates an intervention that is at least n times as effective as the best existing intervention with probability p. If I was to call your construction the "Minimum value of information", it's possible to calculate the "Expected value of [Perfect|imperfect] information", which I feel like might be a more useful number. Guesstimate can do this as well, I could provide an example if you'd like.
We have to remember that we are still uncertain about the cost-effectiveness of the new intervention, which means it would need to be expected to be more cost-effective even after considering all priors. This may increase c or decrease p. However, this is probably irrelevant to the argument.
Amusingly, we seem to come at this at two very different angles, I have a bias that I'd like EA to spend less on research (or less on research in specific directions) and you're here to try and convince EA to spend more on research! Love you're work, I'll get onto your next post and we'll chat soon.
Thank you, Sam!
Yes, I am familiar with the Value of Information, and I am building on it in this project. I have added the “Value of Information” tag.
Yes, this argument assumes that the alternative to investing some funds into R&D is that all the funds are invested into existing interventions/charities. I intended to answer the question ”When is it worthwhile for a grant maker, such as GiveWell, that currently does not fund any R&D projects to invest into the development of new interventions at all?".
I have done that. Those analyses are reported farther down in this post and in follow-up posts.
Good point! One way to accommodate this is to add the cost of determining whether the new intervention is more cost-effective than the previous to the research cost c.