Summary

Quadratic funding (QF) is a mechanism that has gained attention as a potential way to improve resource allocation in a number of philanthropic decision situations. In this post, I explain how the mechanism works, discuss some of its drawbacks, and discuss how these drawbacks relate to several proposed use cases. I argue that its drawbacks severely limit the practical applicability of the mechanism, and that QF will generally not be an attractive option for philanthropic applications.

Introduction

Quadratic funding is a mechanism for providing public goods which was first proposed by Buterin, Hitzig and Weil (2019) (henceforth BHW). It is related to (but different from) quadratic voting, and has attracted attention in the philanthropic space in the past few years. For example, Gitcoin and DoraHacks are two of the main platforms that currently use QF for funding software development, with Gitcoin alone distributing over $50 million using this mechanism. WeTrust has used QF for matching donations. 

The effective altruism (EA) community in particular has also demonstrated interest in the mechanism. Two of its proponents were guests on the 80,000 Hours podcast (Vitalik Buterin and Glen Weyl), the paper proposing the mechanism has been cited in the GPI research agenda, and a number of EA Forum posts discuss it. One project proposal suggested using it to subsidize donations, though to the best of my knowledge it has not yet been employed in EA. (edit: they have implemented it, as mentioned in this comment.)

Some proposed applications of this mechanism include

• Donation matching: campaigns that match individual donations occur in a variety of contexts, such as fundraising campaigns during the giving season. However, the matching rules that these campaigns use (such as a 1:1 matching ratio) are typically set arbitrarily, without any particularly compelling theoretical reason behind their choice. A more principled way of matching donations could lead to higher social gains, and QF could provide a way to do so.
• Donor coordination: when donors have preferences over charitable organizations with some overlapping interests, there might be opportunities for them to reach mutually beneficial agreements. For example, suppose that someone has cause A as a favorite cause and cause B as a close second, while someone else has cause C as a favorite cause and cause B as a close second. In the absence of coordination, they might donate everything to their preferred option, even though they might be better off if both donate everything to cause B. Quadratic funding could help with this coordination process, by internalizing the externality on others through matching funds.
• Grantmaking: organizations and individual grantmakers deciding between different interventions often want to aggregate the o information spread across multiple experts. Or perhaps they may be looking for some more democratic ways to spend their resources, deferring not to people’s knowledge but rather to their preferences. Given that it is often unclear what is the best procedure to aggregate these opinions, QF could serve as an approach to make these allocations.
• General public good provision: many problems that philanthropists face are public good provision problems, and to a large extent philanthropy can be understood as trying to alleviate underprovision problems. For example, pandemic prevention policies generate global externalities, which will be ignored if countries selfishly choose how much funding to dedicate to these policies. Insofar as QF is a promising public good provision mechanism, it could be applied to many of these problems.

I have written a paper on this mechanism, gave a lecture about it during ETGP 2022 (slides), and have spent some time thinking about the mechanism and its potential applications. In this post, I summarize some of the most important aspects of this discussion, and give my overall impressions about the applicability of QF to the use cases mentioned above. Throughout the post, I sacrifice mathematical precision for accessibility and simplicity.

How the mechanism works

The term public good is used to refer to goods which are non-rival and non-excludable. A good is non-rival whenever its consumption by one individual does not prevent other individuals from consuming it.

The quadratic funding mechanism allows every individual $i$ to make a contribution ($c_i$) to a public good, and then matches these contributions so that the final funding level of funding for the public good will be given by

$({\sum }_i\sqrt{c_i}{)}^2$.

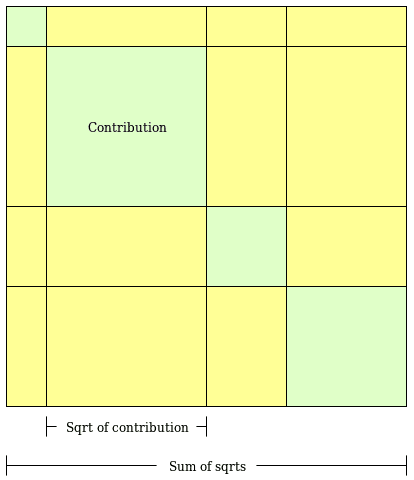
The following figure (from Vitalik Buterin’s explanation of quadratic mechanisms) gives a visual representation of this formula.  If we think of the contribution of each donor as the area of a square (green squares below), QF takes the square root of these areas (side of the green square), sums them, and takes the square of this sum. The resulting funding level is then the total area of the square in the figure. The yellow area represents the amount of money needed to match individual contributions to get to the final provision level.

BHW are the ones to first propose this mechanism. They show that QF is efficient under some (mostly standard) assumptions, which means that it will fund public goods to a level that maximizes social welfare. QF isn’t the only mechanism to provide this efficient level of funding: the most prominent class of solution to the problem in the economics literature are the VCG mechanisms, whose origin dates back to the 1960s.^[1] However, BHW argue that QF has a combination of several other desirable properties that make it particularly desirable as a practical solution to public goods provision. These include

• Simplicity: it is easier to explain how QF works than most other mechanisms in the mechanism design literature, especially for those unfamiliar with economic theory. It is also simpler to run than many of those, as it only requires individuals to report a contribution for each public good, rather than their entire utility functions.
• Flexibility: QF doesn’t require the set of public goods to be specified beforehand, so participants could easily make and vote for new public good proposals. It also doesn’t require one to know who will be the agents participating in the public good.
• Individual rationality: QF doesn’t require anyone to make contributions, so individuals only participate when it’s in their best interest to do so.

BHW also acknowledge that QF has some important limitations, such as the fact that the mechanism generally runs on a budget deficit. They also propose some variations of the mechanism that try to mitigate specific problems with QF, such as funding the budget deficit problem through taxation, or allowing for negative contributions to projects which might be undesirable for some individuals.

Drawbacks

In this section, I discuss in more detail four QF drawbacks which are particularly critical to potential applications. Two of these points (budget deficit and collusion) have already been discussed (by BHW and elsewhere). Additionally, I discuss the inefficiency of this mechanism under incomplete information, and why QF scores lower on usability than what it may look like at first, both of which are points I haven’t seen discussed elsewhere.^[2]

Budget deficit

To develop an intuition for how much funding is provided by QF, here are a few numerical examples.

• If one individual contributes $1 to the public good, then the QF funding for the good will be $(\sqrt{1}{)}^2=1$.
• If two individuals contribute $1 and $2, respectively, to the public good, the QF funding level for that public good is $(\sqrt{1}+\sqrt{2}{)}^2\approx 5.83$.
• If three individuals contribute $1 each to some public good, the QF funding level for that public good is $(3\sqrt{1}{)}^2=9$.

As these examples suggest, the QF funding level is generally higher than the sum of individual contributions. More specifically, the funding level grows with the square of the number of contributions, so if $n$ individuals each contribute some amount $x$ to the public good, the resulting funding level will be $n^{2}x$. Since the sum of individual contributions in this case is $nx$, the only situation where you don’t need external funding is when a single individual contributes to the public good.

Furthermore, as the number of individuals contributing to the public good increases, the fraction of resources that individuals contribute to the public good becomes an arbitrarily small fraction of total funding. This means that, when used for funding public goods that benefit large populations, QF would require a matching pool of money that is approximately all resources that are necessary to fund the public good. This means that QF works as a way of getting people’s preferences about the public good, given that one already has the money necessary to provide the good efficiently, rather than providing a way to raise funds for public goods.

In some applications, the philanthropist running the mechanism may not have enough resources to fund public goods to this efficient level. In such cases, we would want to adjust QF to this restriction, so that we can fund the public good as efficiently as possible without going over the budget available. BHW propose a variation of quadratic funding, called capital-constrained quadratic funding (CQF), which is intended to do this adjustment. When each individual $i$ contributes $c_i$ to the public good, the CQF provision level is given by

$\alpha ({\sum }_i\sqrt{c_i}{)}^2+(1-\alpha \left)\right({\sum }_i{c}_i),$

where $0<\alpha <1$ is a constant chosen to exhaust the budget. This means that a fraction $\alpha$ of individual contributions are matched according to the QF funding rule, and a fraction $(1-\alpha )$ is unmatched. As far as I’m aware, this is the variation of the mechanism that has been implemented in practical applications.

BHW shows that, when the population (number of contributing individuals) is large, the allocation between different public goods is approximately efficient.^[3] This means that we would be using our resources about as well as possible, given a sufficiently large number of participants.

However, there are a few points about CQF and the result above which make this solution less appealing than it looks. First, when the population isn’t large, then this result doesn’t hold. The population size required depends on the value of $\alpha$ (the smaller the $\alpha$, the larger the population needed), and how good an approximation we want. Hence, the threshold to aim for depends on how much inefficiency we’re willing to tolerate. This makes CQF less desirable relative to other mechanisms which are efficient in small populations, and the less so the smaller the value of $\alpha$.

On the other hand, when the population is indeed large, approximately all funding comes from the matching resources, just as in the case of the main QF mechanism. In practice, CQF is spending the matching budget efficiently, rather than using primarily the individual contributions efficiently. This is not a problem in and of itself, but it makes CQF inadequate for applications where the focus is on (primarily) using the contribution resources effectively, such as donor coordination.

Lastly, there is the question of where the $\alpha$ comes from. We cannot simply assume that whoever is running the mechanism knows what the value of $\alpha$ would be necessary to exhaust the budget, as BHW seem to do. As I discuss in more detail in the incomplete information subsection, the informational assumptions they make are such that whoever is running the mechanism does not know the preferences of the contributing individuals. This means that it is not possible to pick the $\alpha$ that would perfectly exhaust the budget one wishes to dedicate to such a project. Hence, in practice, one would have to compromise by doing something like the following:

• Being very conservative, and picking an $\alpha$ that is low enough to guarantee that the funding won’t go over the budget. This solution is unappealing, as (1) not exhausting the budget means that one isn’t able to use as much funding as one intended to for funding the public good, and (2) lower values of $\alpha$ lower the efficiency of the mechanism.
• Letting $\alpha$ be endogenously determined so that it exactly clears the budget. The issue here is that it would result in a different mechanism, which has not been shown to exhibit the efficiency property that BHW proved for CQF.

Vulnerability to collusion

The efficiency result shown by BHW relies on the assumption that individuals are acting selfishly, without any coordination. They acknowledge that when this assumption is relaxed, then groups of individuals could collude to generate mutually beneficial gains, at the expense of the efficiency of the mechanism. Individuals can coordinate to increase the funding to public goods which they like, which would lead such goods to be funded at a level that is higher than the socially optimal level. Furthermore, as highlighted by BHW, this problem doesn’t even require multiple people to cooperate: one individual fraudulently acting as multiple individuals (say, by creating multiple accounts in a platform) would suffice for them to get the benefits of collusion.

As an illustration of the gains from collusion, suppose that someone is the only person to value a public good under consideration. If this individual contributes with $2 to this public good, then the total funding under QF will be $2. If this individual instead contributes $1 to the public good and gets a friend to contribute another $1 to the public good on their behalf, then the total funding for the public good under QF will be $4. 

More generally, by splitting a contribution of $x$ between $n$ individuals, total funding for the public good under QF will be $nx$, which is effectively a matching of $(n-1)x$ to the individual contribution. This has two important implications.

1. Even in the case when only two individuals collude, they can double a given contribution by splitting it equally between themselves. This suggests that large-scale collusion isn’t necessary for obtaining high private benefits from the mechanism, at the cost of the mechanism’s efficiency.
2. Participants can obtain an arbitrarily high matching to a given contribution by splitting the money between a sufficiently large number of individuals. One could turn $1 into $1000 by having 100 people contribute $0.01 to the public good. This issue is particularly worrisome in contexts where participants might be able to fake multiple identities.

Both of these issues apply similarly to CQF, where the gains from collusion from a given contribution downscale in proportion to $\alpha$.

This thread mentions one example of collusion in a practical application of QF.

Inefficiency under incomplete information

Remark: this section is more technical than the rest of the writeup. Non-technical summary: more realistic informational assumptions make QF inefficient, which causes the mechanism to lose its main reason for attractiveness.

When proving efficiency, one of the assumptions that BHW make is complete information about individual preferences/utility functions. This assumption usually entails that (1) every individual knows everyone else's preferences, but (2) whoever is running the mechanism does not know these individual preferences. 

This assumption is realistic, for example, in a court setting, where the goal is to elicit truthful information from individuals who are equally well-informed about a case. However, this is not a realistic assumption in a public good provision setting.^[4] To make it more realistic, we could modify this assumption in two ways. First, we could assume that the institution running the mechanism also knows everyone’s preferences. In this case, it is easy to implement an ideal solution to the public goods provision problem, which satisfies (among others) efficiency and budget balance. Second, we could assume instead a more realistic setting of incomplete information, where the institution running the mechanism doesn’t know individual preferences, and individuals only know their own preferences.^[5] In Freitas and Maldonado (2022), we study this setting.

The main result of our paper is that, except in some special cases, the mechanism will be inefficient when there is incomplete information. The intuition is as follows. The amount that an individual wants to contribute to some public good depends on how much others are contributing to that good. When facing uncertainty about how much others are contributing to the public good, an individual chooses a contribution based on their expectation of the contributions of others, which generally results in inefficiency.

We also study changes in efficiency as the population size grows. We conduct this analysis for a particularly relevant class of utility functions, varying a parameter of this function that determines how quickly marginal utility for the public good decreases as consumption of the public good increases. We find that efficiency can increase or decrease as population grows, depending on the value that this parameter assumes. In cases where efficiency increases, the mechanism is asymptotically efficient, and so QF generates approximately optimal public good provision for large populations. However, even in these cases, QF it will generally be outperformed by a very simple funding rule. My takeaway from these results is that, even though larger populations may make the inefficiency problem less severe, it is unlikely that QF is the best solution for funding public goods in this context.

Finally, I also evaluate a version of QF under incomplete information where individuals report their entire utility functions rather than simply reporting a contribution.^[6] This approach has several theoretical advantages, as it allows for much more general results. The main result from this analysis is also negative: with incomplete information, no (static) mechanism leads to the same outcome as QF under complete information. The intuition behind this result is that the utility function reported by the individual will directly cause changes to the contribution of other individuals, as well as to his contribution. This direct influence from their choice doesn’t occur under complete information, since individuals know how much others truly value the public good, and pick the contributions simultaneously. Hence, when individuals can report their utility functions in QF, individuals will generally have an incentive to report utility functions which are different from their true one, aiming to manipulate the contributions of others. 

This result doesn't rule out the possibility that a dynamic version of the mechanism (say, with multiple rounds) would generate efficiency. But this hasn't been shown, and I suspect that truthful revelation will still be a problem. For example, individuals could gain from contributing more to the public good than they otherwise would, if this also leads others to contribute more to the public good, in a form of what is known as tacit collusion.

In sum, most of the results here are negative. Incomplete information poses a significant challenge to the efficiency of QF, which is the main property used to justify the use of this mechanism.

Usability

One of the main advantages of QF has to do with its simplicity. As I mentioned earlier, its formulation is considerably simpler than many mechanisms in the mechanism design literature. Getting some intuition for how QF works requires only knowledge of high school level math and a few illustrative examples.

However, I believe that the simplicity in its formulation does not translate to simplicity in the practical usage of the mechanism. Even under complete information, figuring out what contributions are optimal for individuals requires relatively complicated calculations, which I don’t expect participants in the mechanism would be able to do well in any widespread application of the mechanism.

Consider the following example. Suppose that 1,000 individuals are contributing to a public good using QF. If we fix the contribution of 999 individuals at $1, the funding level when the thousandth individual also contributes $1 will be $1 million. When this thousandth individual increases their contribution to $2, the aggregate contribution increases by over $800. This indicates that the final funding level can be extremely sensitive to the contribution choice of each individual. To achieve efficiency, individuals must take into account precisely how their contribution will affect the final funding level, in addition to knowing how this change in funding level will affect their utility.

To complicate things further, we cannot make the assumption that individual contributions will stay fixed when calculating how much an individual should contribute. A change in the contribution of one individual also changes the best response of all other individuals, and so everyone else would have a different best-response contribution.

Quadratic funding, as BHW study it, is a static mechanism. This means that all individuals make a contribution simultaneously, without knowing what others will contribute. In practice, if the mechanism is applied in this way, I expect that participants will be extremely uncertain about how much their contributions will affect total funding, and will likely not make an explicit attempt to “try to maximize your utility based on your expectation of how much others are contributing”. Instead, their decision procedure might look like “contribute the amount of money that I would want to donate to this project, and hopefully I will get a nice matching for it”. Needless to say, QF won't be efficient if individuals act in this way.

If QF is used dynamically, where contributors are allowed to see how much total funding will be affected by their donation and adjust their contribution over time, this could alleviate uncertainty about the matching to a large extent. Nevertheless, the mechanism would still feel opaque, and the matching to individual funding should change substantially as everyone adjusts their contributions. I expect that individuals will adjust their contributions relatively little in response to changes in the contributions of others, and will follow similar heuristics to the static case, to a result that they’re somewhat more satisfied with.

Revisiting potential applications

In the introduction, I mentioned four potential philanthropic applications of QF. I now revisit these applications in turn, and comment on how valuable I think QF is for each based on the discussion above.

Regarding donation matching, the budget deficit property is a major drawback. Donation matching programs typically aim not only to give donors some voice over how the matching funding should be spent, but also to stimulate donors to donate more. QF will do a poor job at the latter, especially when there are many donors. This is a problem even with a relatively small number of donors: when we have 10 donors contributing the same amount, 90% of the resources in QF will come from the matching budget. Here, CQF could be an interesting alternative to give more reasonable multipliers, particularly its version with an endogenous $\alpha$. However, these mechanisms will typically do a poor job at getting more donations from individuals. Mechanisms designed specifically for this purpose should do a much better job at increasing donations.

An application to donor coordination is even more severely affected by budget deficit. Here, the goal is precisely to help donors reach mutually beneficial agreements. Perhaps one would be willing to use some external funding to help with the process, but the goal is not to get information about how to spend this auxiliary funding according to individual preferences, but instead getting gains from cooperation. The considerations so far imply that QF or CQF would not do a good job at this.

When it comes to the grantmaking application, I think that the actual decision situation is quite different from the one where QF would be most suited to. Some differences include:

• Experts are not making funding allocations based on selfish maximization of their own utility, which is the underlying assumption in the public good provision problem. Rather, they are trying to use the information that they have to allocate altruistic funding, being guided by their own preferences.
• Experts are not paying out of their pockets to direct the grantmaking process, which is what provides the incentive to decide the right amount to contribute (when they are selfishly maximizing their utility).
• If $n$ experts agree on a giving schedule, then this suggests that the grantmaker can be more confident about that being a good giving schedule, and might want to scale up donations because of that. Nevertheless, there is no good reason why the grantmaker would want to scale up funding by exactly $n^2$ times the funding level when only one expert is consulted (and keep increasing it at this rate the more experts agree with it).

Hence, I don’t think that a public good provision mechanism is what grantmakers are looking for here. Rather, voting mechanisms seem more appropriate to the nature of the task at hand.

Finally, for general public good provision problems, the viability and potential of QF will depend on the context. For global public good provision, I expect that budget deficit would be a major challenge if not using government-level budgets, and a CQF with a small budget would generate substantial inefficiency even under complete information. I expect that inefficiency, budget deficit, and usability issues would make QF and its variations unattractive in a number of these circumstances.

Conclusion

After studying QF formally and spending time thinking about the mechanism, I’m not excited about applying it in situations that have been suggested so far. I believe that a lot of this excitement about this mechanism comes from excitement about quadratic voting, rather than from careful thinking about the characteristics of QF on its own.

I could become more optimistic about QF if subsequent studies can prove some desirable theoretical properties for variations of this mechanism which I’ve mentioned above. These include approximate efficiency of CQF with an endogenous $\alpha$, and (asymptotic) efficiency of some dynamic version of QF. I could also become more optimistic about the mechanism if we get some compelling results from its practical applications. As far as I’m aware, Gitcoin is the organization that has applied QF the most, and so might have data to be analyzed here. Nevertheless, I doubt that these research directions are more promising than, say, building expertise on mechanism design more broadly. For the philanthropic applications I discuss here, it seems to me much more promising to design mechanisms targeted at the specific goals of those decision situations, rather than more general-purpose mechanisms.

I close this post with my impression on quadratic voting. While I haven’t worked on this mechanism, I’m more optimistic about quadratic voting than I am about QF, and I would be excited about more research on it. Differently from QF, it makes use of the fact that individuals have incomplete information, rather than relying on assumptions of complete information, and this paper shows that quadratic voting is efficient under incomplete information. But quadratic voting stands out less to me than to most people in the EA community. This is partly because if I were to study it, I expect I would learn about some potentially important limitations (which I’m currently unaware of), as has happened to me with QF. But my lower relative excitement also comes from a higher excitement about other promising but less well-discussed voting mechanisms, such as score voting, approval voting, storable voting, and liquid democracy.

I'm grateful to Loren Fryxell, Lennart Stern, Benjamin Tereick, and Philip Trammell for discussions which helped me improve my understanding of QF and the applications I discuss. I thank Gustav Alexandrie and Benjamin Tereick for comments on a draft of this post.

1. ^{^}

   See Mas-Colell, Whinston and Green, 1995, Microeconomic theory.

2. ^{^}

   I won't discuss the desirable properties of the mechanism in detail in this writeup. This is primarily because I believe that the drawbacks I discuss make QF an unattractive mechanism for philanthropic applications, as I discuss in the potential applications section. For more discussion of these properties, I recommend reading the resources linked in the introduction of this post.

3. ^{^}

   Here, and in the rest of this post, when I mention large populations, I’m referring to asymptotic results: when population size goes to infinity, some property holds arbitrarily well.

^{^}

Public good provision games generally do not assume complete information. For example, the aforementioned VCG mechanisms are shown to be efficient under incomplete information.

^{^}

In this setting, individuals have common knowledge of the probability distribution of preferences of all other individuals.

^{^}

 In technical terms, I follow a direct revelation approach. These results are not in the paper, but I explain the logic behind them in these slides.

Show all footnotes