Summary
- I calculated the welfare ranges per calorie consumption for a few species.
- They vary a lot. The values for bees and pigs are 4.88 k and 0.473 times as high as that for humans.
- They are higher for non-human animals:
- 5 of the 6 species I analysed have values higher than that of humans.
- The lower the calorie consumption, the higher the median welfare range per calorie consumption.
Methods
I calculated the welfare ranges per calorie consumption from the ratio between:
- Rethink Priorities’ 5th percentile, median, and 95th percentile welfare ranges.
- Calorie consumption per day for mature individuals. Note there is variation within the same species.
My calculations are here.
Results
The results are below by descending median welfare range per calorie consumption.
Welfare range and calorie consumption
Species | 5th percentile welfare range | Median welfare range | 95th percentile welfare range | Calorie consumption (kcal/d) |
|---|---|---|---|---|
Bees[1] | 0 | 0.071 | 0.461 | 0.0327 |
Shrimp[2] | 0 | 0.031 | 1.149 | 0.831 |
Crayfish[3] | 0 | 0.038 | 0.491 | 4.88 |
Salmon[4] | 0 | 0.056 | 0.513 | 34.9 |
Chickens[5] | 0.002 | 0.332 | 0.869 | 300 |
Humans[6] | 1 | 1 | 1 | 2.25 k |
Pigs[7] | 0.005 | 0.515 | 1.031 | 2.45 k |
Welfare range per calorie consumption
Species | 5th percentile welfare range per calorie consumption (d/kcal) | Median welfare range per calorie consumption (d/kcal) | 95th percentile welfare range per calorie consumption (d/kcal) |
|---|---|---|---|
Bees | 0 | 2.17 | 14.1 |
Shrimp | 0 | 0.0373 | 1.38 |
Crayfish | 0 | 7.79 m | 0.101 |
Salmon | 0 | 1.61 m | 0.0147 |
Chickens | 6.67 μ | 1.11 m | 2.90 m |
Humans | 0.444 m | 0.444 m | 0.444 m |
Pigs | 2.04 μ | 0.210 m | 0.421 m |
Species | 5th percentile welfare range per calorie consumption as a fraction of that of humans | Median welfare range per calorie consumption as a fraction of that of humans | 95th percentile welfare range per calorie consumption as a fraction of that of humans |
|---|---|---|---|
Bees | 0 | 4.88 k | 31.7 k |
Shrimp | 0 | 83.9 | 3.11 k |
Crayfish | 0 | 17.5 | 226 |
Salmon | 0 | 3.61 | 33.1 |
Chickens | 1.50 % | 2.49 | 6.52 |
Humans | 1.00 | 1.00 | 1.00 |
Pigs | 0.459 % | 47.3 % | 94.7 % |
Discussion
The median welfare ranges per calorie consumption vary a lot. The values for bees and pigs are 4.88 k and 0.473 times as high as that for humans[8].
In addition, the values are higher for non-human animals. 5 of the 6 species I analysed have values higher than that of humans. Moreover, the lower the calorie consumption, the higher the median welfare range per calorie consumption. These suggest welfare can be created more efficiently via small non-human animals. However, one should also account for:
- The energy needed besides that in food.
- The level of welfare as a fraction of the median welfare range.
I would still guess that it is possible to achieve higher total welfare with mostly small non-human animals, in agreement with animal welfare arguably being dominated by that of arthropods and nematodes. In the future, one might be able to produce welfare much more efficiently via non-biological beings.
- ^
According to Mark Patterson, “in summer a full strength Honey Bee hive contains around 50-60,000 workers and needs to consume around 1800 calories per day”. So I used 0.0327 kcal/d (= 1.8/((50 + 60)/2)).
- ^
A shrimp of 40 g is fed 0.84 g/d (= 0.021*40), and shrimp feed has 0.989 kcal/g (= 84/(3*28.3)). So I used 0.831 kcal/d (= 0.84*0.989).
- ^
- ^
“After two years at sea”, adult salmon have “8 to 12 pounds”, so it grows 6.21 g/d (= (8 + 12)/2*454/(2*365.25)). In addition, “Atlantic salmon needs 1.15 kg feed to gain 1 kg body weight”, which translates into 7.15 g/d (= 6.21*1.15) of feed, which contains 4.88 kcal/g (= (0.356 + 0.110)*4 + 0.335*9). So I used 34.9 kcal/d (= 7.15*4.88).
- ^
According to Ken Macklin and Joe Hess, “a hen may consume up to 340 calories of metabolizable energy per day during winter to keep warm. But in summer, she may consume only 260 calories of metabolizable energy per day”. So I used 300 kcal/d (= (260 + 340)/2).
- ^
According to the National Health Service, “the recommended daily calorie intake is 2,000 calories a day for women and 2,500 for men”. So I used 2.25 k kcal/d (= (2 k + 2.5 k)/2).
- ^
Mean between the lower and upper bounds of 2.4 k and 2.5 k for breeder pigs.
- ^
Fun fact, I was stung by a bee/wasp just today.

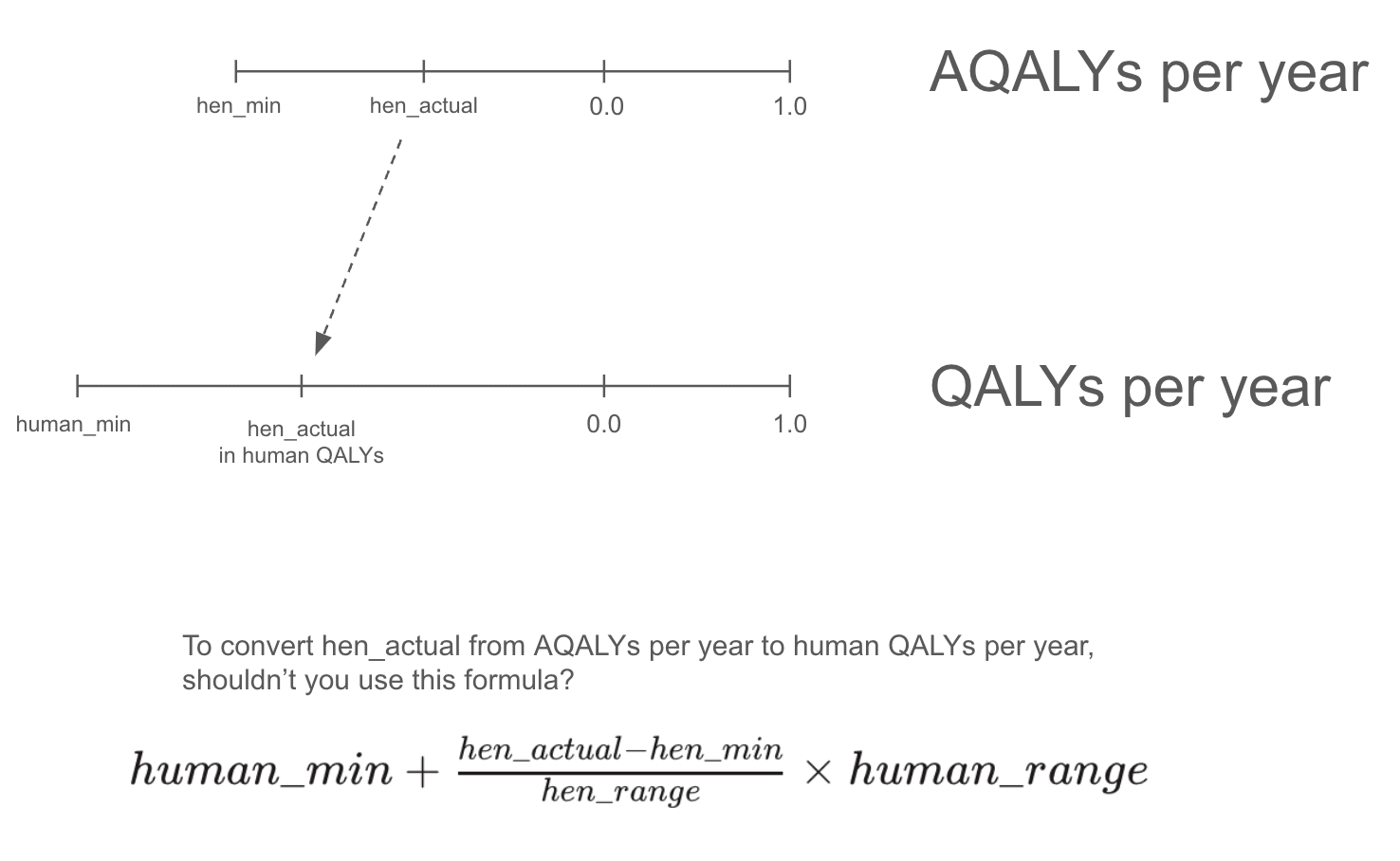




Hi Vasco, I'm not sure Food Impacts is calculating things correctly. They start off by calculating the number of animal hours lived to create 2,000 calories, which is reasonable. The next step should be to multiply that number by the average welfare of an animal, since that should tell you how many negative welfare units would be averted by not creating the demand for 2,000 calories.
But instead, they multiply by the welfare range of the animal.
This doesn't make sense to me. If a farmed cow's actual welfare is -0.1, why does it matter that its welfare range is -0.25 to 0.25? To figure out how much negative welfare I can avert, I care about the -0.1!
Am I thinking about this correctly?
And if so, is there a good resource for actual welfare values for farmed animals, rather than the theoretical ranges?